多进制高斯信道下四进制LDPC码的实现

李春腾 ，蒋宇中 ，宫 烨 ，张百勇

(1.海军工程大学 电子工程学院，湖北 武汉 430033；2.海军工程大学，湖北 武汉 430033)



多进制高斯信道下四进制LDPC码的实现

李春腾1，蒋宇中1，宫 烨1，张百勇2

(1.海军工程大学 电子工程学院，湖北 武汉 430033；2.海军工程大学，湖北 武汉 430033)

四进制低密度校验码( Low-Density Parity-Check Code，LDPC)具有较好的抗突发差错性能。为了进一步改善系统的性能并适当降低其复杂度，在二进制LDPC码的基础上，主要研究短码长四进制LDPC码，并在原有串行译码算法的基础上对其改进，提出一种基于校验点准确度的串行译码算法。仿真结果表明，在多进制高斯信道条件下，对于短码而言，改进的串行译码算法性能要优于串行译码算法，在误码率为10-2时，能获得0.25 dB的编码增益。

四进制LDPC码；多进制高斯信道；译码算法；准确度

0 引言

虽然香农在1948年界定了信道编码[1]的性能，但是在Turbo码出现之前，大部分信道编码算法都远远达不到香农限。因此Turbo码的出现标志着加性高斯白噪声(AWGN)信道下信道编码开始接近香农限。1995年，在Turbo码的启发下，Mackay和Neal重新发现了长时间被遗忘的低密度校验(LDPC)码具有更加接近香农限的性能。LDPC码是Gallager[2]于1962 年提出的一类基于稀疏校验矩阵的线性分组纠错码。按照稀疏校验矩阵定义的LDPC码，每个码字满足许多线性约束。Gallager提出了LDPC码的构造方法、迭代概率译码算法和理论分析。但是由于编译码的复杂度以及Reed-Solomon码和级联码的出现，LDPC码并没有得到足够的重视。

Turbo码虽然在3G通信标准中占据主导地位，但是LDPC码与它相比在某些方面有着明显的优势：LDPC码所采用的迭代概率译码算法是并行算法，可以实现并行操作，有利于硬件的实现；并且LDPC码是根据稀疏校验矩阵定义的，所以其本身就有很好的抗突发差错的性能，不需要引入交织器，减少了时延。这些优势使LDPC码在信道条件较差的无线移动通信中展现了很大的应用前景，适合于在未来的通信系统中实现。

多进制LDPC码是LDPC码的一种特殊形式，有实验表明，其抗突发差错性能相比于二进制LDPC码有较大程度的改善[3-4]。目前，对二进制LDPC码的编译码技术已基本成熟，对多进制的研究也取得初步的成果，但都是基于二进制AWGN信道下。本文将在多进制AWGN信道下，根据二进制LDPC码中的编译码基础，来实现四进制LDPC码的编译码并进行相应的性能分析。

1 四进制LDPC码的编码

对于编码过程而言，类比于二进制LDPC码的编码过程，四进制中用到的是具有近似系统形式的H矩阵的快速编码[5]。已知一个码字U，奇偶校验矩阵为H。编码之前的信息源为S。假设编码后S位于U的后部，校验位C位于U的前部，即U=[C|S]。下面对矩阵H进行分解，即H=[A|B]，而后对A进行行变换，使其成为可逆矩阵，这样得到的矩阵A是一个M×M大小的，B是一个M×(N-M)大小的矩阵。因此可以得到：

U·HT=0；

(1)

利用上述分解，进而可以得到：

AC+BS=0。

(2)

通过上式在四元伽罗华域中的运算，就可以得到校验位，将校验位和信息位合并就得到编码之后的码字。

最初得到的矩阵H往往达不到矩阵A可逆的要求，因此需要对矩阵H进行行列交换，这样可以保证在绝大多数的情况下可以将矩阵H转换成可逆矩阵A和B矩阵的乘积。这里对矩阵H进行行交换，相当于交换了校验点的位置，并不会影响矩阵H的编码结果，而列交换相当于对码字的顺序进行重新排列，在编码结束后按照交换的顺序进行反变换，就可得到原矩阵H对应的编码后的码字。

2 四进制LDPC码的译码

2.1 洪水译码算法

对于译码过程，同样类比于二进制的译码过程，用到的也是信度传播[6](Belief-propagation，BP)算法[7-8]。对于四进制BP算法而言，其和二进制的过程大体一致，主要包括初始化、校验点更新、量点更新和判决。该算法中心思想就是利用校验方程得到变量满足四元域的约束关系，通过迭代运算来进行纠错。为了使译码过程更容易理解，先引入如下变量：

代表矩阵H的行重(每行非零元素的个数)，代表矩阵H的列重(每列非零元素的个数)，a代表四元域中的某个元素(用数值0、1、2、3来代表四元域中的4个元素)；

m代表矩阵H的校验方程的个数(即行数)，n代表矩阵H的变量的个数(即列数)；

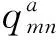
N(m)，与第m个校验点相邻的所有变量；M(n)，与第n个分量相邻的所有校验点；N(m) ，与第m个校验点相邻的除了第n个分量之外的其他所有分量；M(n)m，与第n个分量相邻的除了第m个校验点之外的其他所有校验点。

(1) 初始化

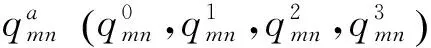
可得初始化概率为：

(3)

(2) 校验点更新

这相当于校验点的计算过程，注意四进制的运算要满足上述四元域的运算法则。假设矩阵H中的第一个校验方程为3x3⊕2x5⊕3x7=0，利用全概率公式可以得到满足其约束条件的4个条件概率的相加：

(4)

(3) 变量点更新

这一步工作是变量点的计算，看作是重复节点的计算。

(5)

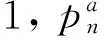
(4) 判决

最后得到后验概率为：

(6)

得到后验概率后，对每一个变量点选择概率最大的那个，将其所对应的a的值就作为该变量节点的最后译码结果。这样就得到了一个新的码字序列vhat，如果vhat·HT=0，则译码成功，否则就转到第二步，继续进行迭代直至达到预设的最大迭代次数。

2.2 串行译码算法

该算法同上述译码算法的过程类似，其中更新步骤的运算以及判决步骤和洪水译码[9-10]算法一样。区别在于洪水译码算法在译码的过程中，要等校验节点全部更新完之后，变量节点才开始更新；而串行译码算法[11-12]则是每更新完一个校验节点或者变量节点，就对其相邻的所有变量节点或校验节点进行更新，这样能够使之后要更新的节点及时利用到相邻节点的最新信息，从而加快收敛速度。

该算法的具体步骤如下：

2：for任意一个校验点m

3：for集合N(m)中任意一个n

5：for集合M(n)m中任意一个m′

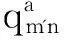
7：endfor

8：endfor

9：endfor

10：ifvhat·HT=0未被满足且未达到预设的最大迭代次数，则返回第2步

11：end if

2.3 改进串行译码算法

上节所提到的串行译码算法在每次迭代时都是按照校验节点的排列顺序进行更新，并没有对其更新的优先级进行区分。下面提出一种基于校验节点准确度的串行译码算法对信息的更新顺序进行排列。

在四元域中，信号在经过多进制AWGN信道之后，由于受到高斯白噪声的影响，在接收端收到的值可能是四元域中的任意一个元素，概率值越大意味着取该元素值的可能性越大，但并不能保证取最大概率值的那个域元素就是之前发送的那个值，因此，在每次迭代运算中都要作比较，如果相同，则进行下一个；如果不同，则称之为错误码位，并找到其对应的变量节点。如果该变量节点的最大概率与次最大概率值相差很大，则说明该变量节点的准确度很低，对误码性能的影响很大，需要优先更新其相邻的校验节点。因此定义准确度V_A为错误码位对应的变量节点的次最大概率与最大概率之差。校验节点相邻的所有变量节点对其准确度都有影响，但是其中准确度最低的对其影响最大。因此，校验节点的准确度M_A定义为与其相邻的变量节点的准确度的最小值。

该算法的具体步骤如下：

2:for 集合N(m)中任意一个n

3：if pn,max对应的域元素不等于编码后对应的码字中的那一位

4：将该变量节点加入集合C中

5：end if

6:end for

7：for 集合C中的变量节点nc

8：计算该变量节点的准确度V_A=pnc,sub_max-pnc,max

9：end for

10：for 除了集合C之外的其他变量节点

11：其准确度置为0

12：end for

13：for 集合M(n)中任意一个m

14：计算校验节点的准确度M_A等于与其相邻的变量节点的V_A的最小值

15：end for

16：校验节点按准确度的升序进行排列

17：for集合M(n)中任意一个m

18： for集合N(m)中任意一个n

20： for集合M(n)m中任意一个m′

22： end for

23： end for

24：end for

25：if vhat·HT=0未被满足且未达到预设的最大迭代次数，则返回第2步

26：end if

2.4 算法分析

对q元LDPC码的串行改进算法进行复杂度分析。假设校验矩阵H是m行n列，行重为dc，列重为dv。为了方便分析和比较算法的复杂度，从初始化准则、译码准则、停止准则3个方面对其进行分析。并且认为该算法的初始化以及停止准则和串行算法一样，每次迭代时信息更新的内容以及传递次数也与串行算法大致相同，不同的是该算法信息更新的顺序却在不断发生变化，这就涉及到为获取节点准确度而增加额外计算量去选择要更新的节点，因此，与串行译码算法相比，改进串行译码算法增加了节点准确度的运算。准确度的获取需要先比较最大概率对应的值与发送的是否相同，如果不相同，再进行最大概率与次最大概率的差值运算，如果相同，则准确度置为0。所以，对于每个变量节点而言，最多需要n(q-1)+n+n(q-2)次实数比较和一次实数加法运算。对于校验节点的准确度，需要找到相邻变量节点中准确度最低的，因此每个校验节点需要dc-1次实数比较，而后还要根据校验节点的准确度对其进行升序排列，因此需要O(mlog(m))次实数比较。

3 仿真结果与分析

实验1中采用(72，2，3)四进制码，码率为1/3，信源发送出的消息经信源编码之后经过四进制LDPC编码，再将编码后的码字通过多进制高斯信道，引入加性高斯白噪声，在接收端经过四进制LDPC译码，将从噪声中提取出来有用的信息转换成经信道之前所编的码字，将其与之前的码字作对比，并进行误码率分析；另一种情况,信源发出的信号经过信源编码之后不经过LDPC编码直接经过多进制高斯信道，引入加性高斯白噪声，采用码长为N=80 000。从图1可看到，在信噪比为0时，没有LDPC编译码的误码性能要优于有LDPC编译码的，在低信噪比的情况下，没有LDPC编译码的误码性能与有四进制LDPC编译码的性能相差不大；随着信噪比的逐渐提高，有LDPC编译码的误码性能要明显优于没有LDPC编译码，这说明LDPC码对通信系统的可靠性起着重要的作用。这是由于LDPC译码算法中引入了迭代运算，通过变量之间的约束关系使得判决更加准确，从而达到纠错的目的。

图1 GF(4)上LDPC码的误码率分析对比

实验2采用GF(4)上的四元LDPC码，该码长为48，码字的信息位为16，码率为1/3，最大迭代次数为5，在多进制高斯信道下对不同的译码算法的进行误码率分析。校验矩阵的行重为3，列重为2。从图2可看出，洪水译码算法的性能曲线是最差的。在低信噪比区域，改进串行译码算法的性能要明显优于串行译码算法，随着信噪比的提高，改进串行译码算法的性能略优于串行译码算法。当误码率为10-2dB时，改进串行译码算法相比于洪水译码算法能获得0.6 dB的编码增益，与串行译码算法相比，能获得约0.25 dB的编码增益。这是由于在低信噪比区域，受高斯白噪声影响较大，导致错码的位数相对较多，而改进串行译码算法在每次迭代时，会根据节点的状态来优先对准确度最差的节点进行更新，即优先纠正错误的码位，从而避免造成差错传播。随着信噪比的提高，错码的位数越来越少，因此改进串行译码算法的信息更新顺序和串行译码算法的大致相同，从而二者的性能也近乎相同。

图2 四进制LDPC码不同译码算法的误码率分析

4 结束语

在二进制LDPC编译码的基础上，重点研究了在多进制信道下的四进制LDPC码，并提出一种基于校验节点准确度的串行译码算法，对信息的更新按照准确度由低到高的顺序进行，从而在一定程度上改善了误码性能。另外，本文对构造的矩阵H进行了简化，限制了其行重为3，从而列重也被限制，也使得列重这一重要的参数没有参与最佳化过程，因而误码性能会受到一定的影响，这一点有待改进。

[1] 孟德香，梁红玉，吴伟陵.基于同步时间拓展处理的信道编码[J],无线电工程，2004,34(3):7-9.

[2] Gallager R.Low- Density Parity- Check Codes [M].Cambridge,Masscahusetts:MIT Press,1963.

[3] Davey M C,Mackay D J C.Low Density Parity Check Codes over GF(q)[J].IEEE Communication Letter.,1998,2:165-167.

[4] Davey M C,Mackay D J C.Low Density Parity Check Codes over GF(q)[C]∥in Proc.IEEE Inform.Theory workshop 1998:70-71.

[5] McEliece J R.The Theory of Information and Coding [M].New York:Cambridge University Press,2002.

[6] Kschischang F R,Frey B J.Iterative Decoding of Compound Codes by Probability Propagation in Graphical Models [J].IEEE Journal on Selected Areas in Communications,1998,16(2):219-230.

[7] Kschischang F R,Frey B J,Loeliger H.Factor Graphs and the Sum-product Algorithm [J].IEEE Transactions on Information Theory,2001,47(2):498-519.

[8] GuilloudF,Boutillon E,Tousch J,et al.Generic Description and Synthesis of LDPC Decoders[J].Communications IEEE Transactions on,2007,55(11):2084-2091.

[9] 吴晓丽，孟 涛．一种改进的多进制 LDPC 码的译码算法[J]．空军工程大学学报(自然科学版)，2009，11(4)：73-77．

[10]Tian Tao,Jones C,Villasenor J D,et al.Construction of Ireegular LDPC Codes with Low Error Floors[C]∥ Proceedings of ICC,2003,5:3125-3129.

[11]张小花.LDPC码的译码算法研究[D].太原：太原理工大学，2012.

[12]岳 田,裴保臣.LDPC码的几种译码算法比较[J].无线电通信技术,2006,32(4):24-26.

Implementation of 4-ary LDPC Codes under Non-binary AWGN Channel

LI Chun-teng1,JIANG Yu-zhong1,GONG Ye1,ZHANG Bai-yong2

(1.College of Electronic Engineering,Naval Univ.of Engineering,Wuhan Hubei 430033,China;2.Naval Univ.of Engineering,Wuhan Hubei 430033,China)

4-ary LDPC(Low-Density Parity-Check)Code has better performance of resistance to burst errors.To improve performance and reduce the complexity of algorithm,this paper mainly about the research of 4-ary LDPC codes with a short code length based on binary LDPC codes.Based on the layer belief propagation,this paper proposes serial decoding algorithm based on the accuracy of check node.Under non-binary AWGN channel,in terms of a short code length,simulation results show that the performance of improved serial decoding algorithm is better than layer belief propagation,it can achieve 0.25dB performance gain at the symbol error rate of 10-2.

4-ary LDPC；non-binary AWGN channel；decoding algorithm；accuracy

10.3969/j.issn.1003-3114.2016.06.22

李春腾，蒋宇中，宫 烨，等.多进制高斯信道下四进制LDPC码的实现[J].无线电通信技术,2016,42(6):86-90.

2016-07-07

李春腾(1992—)，男，硕士硕士生，主要研究方向：通信理论与技术。蒋宇中(1963—)，男，教授，博士生导师，主要研究方向：通信信号处理、低频大气噪声。

TN911.22

A

1003-3114(2016)06-86-5