基于计算-转发策略的双向中继通信方案
2016-12-20王海龙闫泽涛
王海龙,王 钢,闫泽涛
(1.哈尔滨工业大学 通信技术研究所,黑龙江 哈尔滨 150001;2.深圳航天科技创新研究院,广东 深圳 518057)
基于计算-转发策略的双向中继通信方案
王海龙1,王 钢1,闫泽涛2
(1.哈尔滨工业大学 通信技术研究所,黑龙江 哈尔滨 150001;2.深圳航天科技创新研究院,广东 深圳 518057)
针对双向中继通信中物理层网络编码的应用,采用基于计算-转发的中继策略,研究并推导了在AWGN信道和衰落信道下的可达速率。为了在衰落信道下获得更高的传输速率,提出了一种采用信道反转预编码的新型传输方案。对比可知,采用这一预编码方案可使通信性能获得较大提升。在两种信道条件下,基于计算-转发的双向中继通信方案都能获得最大自由度,表明计算-转发策略是当前最适于双向中继通信的中继策略。
计算-转发;双向中继;物理层网络编码;格码;预编码
0 引言
近几年,物理层网络编码(Physical Layer Network Coding,PNC)是无线通信领域的热点话题之一,吸引了大量的学者进行相关研究[1-2]。在有线网络中,网络编码的基本思想是中间节点转发其接收数据包的某一组合方程,而不是多个单独的数据包[3],进而可以提高网络的吞吐量。随后有3组不同研究团队几乎同时将其思想引入到了无线网络中,提出了物理层网络编码[4]、模拟网络编码[5]的概念,以及相关理论上的研究[6]。其核心都是通过电磁波天然的叠加性质实现对多个无线信号的组合,即在物理层实现网络编码运算。研究表明,在由两个源节点和一个中继节点组成的双向中继信道(Two-way Relay Channel,TWRC)模型中,可允许两个源节点同时发射信号,中继节点对两个源信号的模2和(即异或值)进行译码和转发,此方法可以大大提高该模型下的吞吐量。自此,物理层网络编码由于具有能够显著提高无线网络吞吐量的潜力,吸引了诸多学者的兴趣。研究的目标是如何利用物理层网络编码进一步提高无线中继网络的传输速率或容量。
2011年,Nazer和Gastpar为无线中继网络提出了一个新的中继策略:计算-转发策略[7]。其基本思想是通过采用格码(lattice codes),对多址干扰加以利用而不是抑制,进而可以提高网络吞吐量。在这一中继策略中,多个源节点同时发射信息,但中继节点不单独恢复出这些信息,而是希望对这些信息的某一整数线性组合(即方程)进行译码并将其传递给目的节点。目的节点从多个中继处接收到足够数量的方程后,便可以通过解这些线性方程而得到原始的多个信息。
双向中继信道模型来源于双向中继通信,即两个源节点通过一个中继节点互换信息,且二者之间没有直达链路。若采用传统存储转发方式,受半双工工作方式限制,需要4次信道占用(即时分多址接入方式中的4个时隙)完成两个数据包互换;而采用物理层网络编码只需2次信道占用即可完成。典型的物理层网络编码过程包含两个阶段:多址阶段和广播阶段[8]。在多址阶段,两个源节点同时发送信息给中继节点,中继对其某一组合形式进行译码;在广播阶段,中继节点将这一原始信息组合广播给两个源节点。
1 计算-转发中继策略
在计算-转发中继策略中,由于要求码字的整数线性组合仍然是码本中的一个码字,所以目前仍都采用线性码。格码不仅能满足上述要求,还具有诸多其他良好性质,因此在计算-转发策略中得到广泛应用。
计算-转发策略是为一般化的无线中继网络而提出的,网络模型中通常存在多个源节点和多个中继节点,如图1所示。
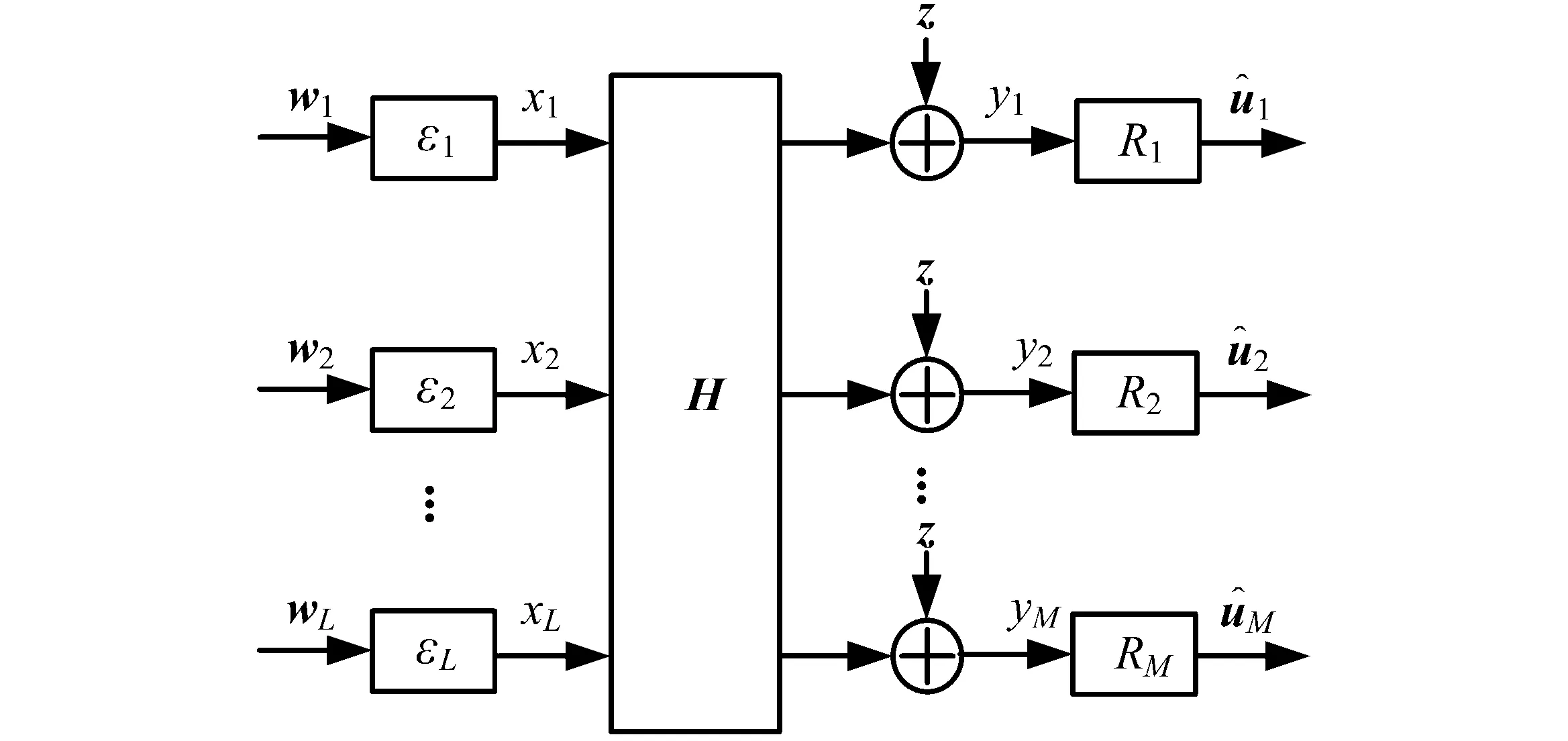
图1 一般化无线中继网络
1.1 编码过程
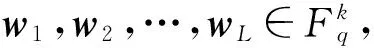
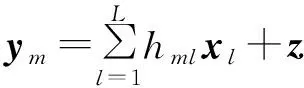
(1)
式中,n维的码字需要满足平均功率限制,即(1/n)E‖xl‖2≤P。信道为加性高斯白噪声信道,则z为循环对称复高斯随机向量,即z~CN(0,σ2In),式中,In为n×n的单位矩阵。
1.2 译码过程
假设中继节点能够获得所有源节点到该中继节点之间的信道系数。每个中继的任务是译码恢复出所有源节点发射码字的一个整数型线性组合:
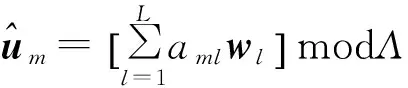
(2)
式中,aml∈+j是译码过程中所选取的系数,选取准则为最大化可达速率。
每个中继节点完成译码后,将得到的线性方程转发给目的节点。目的节点接收到足够数量的线性独立方程后,即可恢复出所有源节点所发射的消息。
计算-转发策略中常用的译码方法如图2所示。

图2 计算-转发中的译码流程
译码过程主要包括两步,首先根据最优比例系数对接收信号进行缩放,其次将缩放后的信号量化到最近的格点[9]。在复数信道AWGN网络中,当信道系数向量为hm=[hm1,hm2,...,hmL]∈L、译码时方程系数向量为am=[am1,am2,...,amL]∈{+j}L时,所能达到的计算速率(computation rate)为[7]:
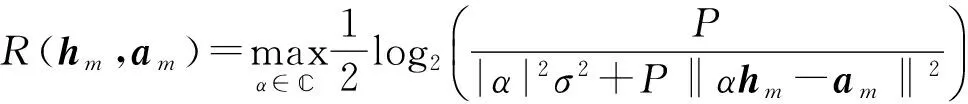
(3)
能够使计算速率最大化的α取值为其MMSE系数值,即:
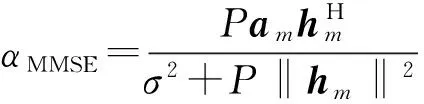
(4)
将上述最佳比例系数值带入式(3),即可得到计算速率的最终表达式。
2 双向中继通信在AWGN信道的可达速率
2.1 双向中继信道
首先给出如下假设:
① 本文采用基于计算-转发策略的物理层网络编码方案,其容量主要由中继节点处的可达速率所决定,为此可只考虑中继处的可达速率;
② 在不采用预编码时,每个用户的平均发射功率为P,同时两用户的速率为对称速率;
③ 为便于性能比较,当采用信道反转预编码时,总的平均发射功率设为2P;
④ 在衰落信道中,信道系数的取值为复数值;
⑤ 每个接收机处的接收信号先按MMSE比例系数进行缩放,然后再进行格译码。
2.2 AWGN信道的可达速率
在第1个时隙,即多址传输阶段,两个源节点同时发射信号,中继节点则对这两个用户发射码字的一个整数线性组合进行译码。对于AWGN信道来说,信道系数h1=h2=1均为整数,则译码时整数线性方程的最佳系数等于信道系数即可。式(4)中的MMSE比例系数为αMMSE=2P/(σ2+2P)。等效噪声为:
(5)
此时的可达速率为:
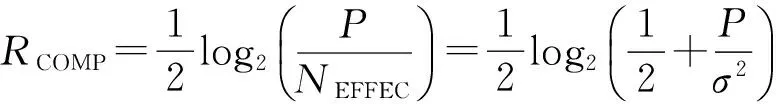
(6)
图3给出了计算-转发中继方案与传统四时隙的存储转发方案、三时隙的网络编码方案、译码-转发和放大-转发方案的可达速率对比。其中后几种传输方案参见文献[1,8],此处不再赘述。由图3可知,采用计算-转发的中继传输方案,其性能表现良好,且在高SNR区域获得的性能提升更大,更接近理论上界。
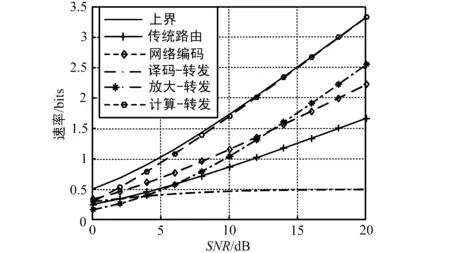
图3 AWGN信道下不同中继方案的可达速率
2.3 计算-转发在双向中继信道中的优势分析
对双向中继通信来说,与其他中继策略相比,基于计算-转发的物理层网络编码方案具有两个主要优势。首先,在传输过程中,由于每个目的节点只需译码单个消息(即对方消息),因此只需要一个整数线性方程,而中继节点总是能够提供这一方程。其次,在具有多个源节点和多个中继节点的一般化中继网络中,当信道为AWGN信道时,中继节点难以为一个目的节点提供足够多的、相互独立的整数线性方程。但对于双向中继信道来说,由2.2节可知AWGN信道非常适于计算-转发策略。实际上,通过下一节在衰落信道中的应用也可验证以上结论。
3 双向中继通信在衰落信道的可达速率
分别考虑没有预编码和有预编码的情况。
3.1 发射端无预编码
此时的双向中继信道模型即计算-转发策略中用户数为2的情况,可达速率直接由计算速率表达式(3)给出:
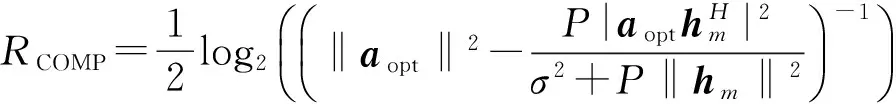
(7)
式中,aopt=[a1,a2]为最优的整数系数向量,与信道系数向量h=[h1,h2]相互独立。
3.2 发射端执行无约束的预编码
在具有多个源节点和多个中继节点的一般化无线中继网络中,由于每个源节点都具有到多个中继节点之间的多个路径,因此源节点无法进行预编码。但双向中继信道中只有一个中继节点,因此在多址阶段,两个源节点到中继节点之间的信道衰落可通过预编码来完全抵消。但需指出,广播阶段同样无法对中继节点的发射信号进行预编码。
在多址阶段,假设每个源节点的瞬时发射功率可以任意高,则可在发射端执行信道反转预编码,使得中继处的接收信号保持为y=x1+x2+z,此时与AWGN信道的情况完全相同。具体说来,两个用户发射信号时分别用1/h1和1/h2对各自信号进行预编码,此时对应的发射功率则变成P/|h1|2和P/|h2|2。
考虑到由于预编码而引起发射功率的变化,采用计算-转发策略的物理层网络编码方案的可达速率为:
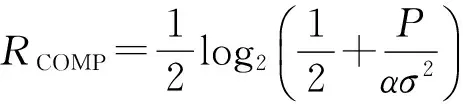
(8)
其中,总的瞬时功率变化系数由下式给定:
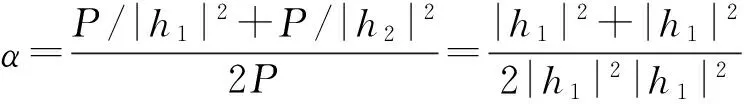
(9)
每个用户每时隙能够获得的可达速率为式(8)中速率的一半。
3.3 发射端执行信道感知的预编码
由于实际发射机工作时的发射功率不能做到任意高,而是存在某一上限,因此前述预编码方案在实际应用中可能存在问题,即当信道增益过小时,信号发射时的预编码系数过大而使得瞬时发射功率超过实际上限。为克服此问题,在这一小节提出一种信道感知的预编码方案。
假设平均发射功率为P,瞬时发射功率的上限为PLIMIT,则信道感知的预编码过程如下:
① 如果两个源节点到中继节点的信道状态都较好,即P/|h1|2≤PLIMIT,且P/|h2|2≤PLIMIT,则两个用户均执行预编码,且整个传输过程按照计算-转发策略进行。
② 如果两个源节点到中继节点的信道状态都过差,即P/|h1|2>PLIMIT,且P/|h2|2>PLIMIT,则两个用户均不发射信号,此时可节省发射功率。
③ 如果有一个源节点到中继节点的信道状态较好,即P/|h1|2≤PLIMIT,或P/|h2|2≤PLIMIT,则信道状态较好的用户执行预编码并发射信号,另一个用户则不发射信号。此时发射信号的用户可获得单用户速率的上限。
根据以上预编码方案,每用户每时隙的平均可达速率可表示为:
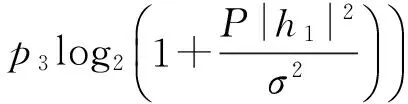
(10)
式中,p1为h1和h2均较好,p2为只有h1较好,p3为只有h2较好的概率。
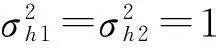
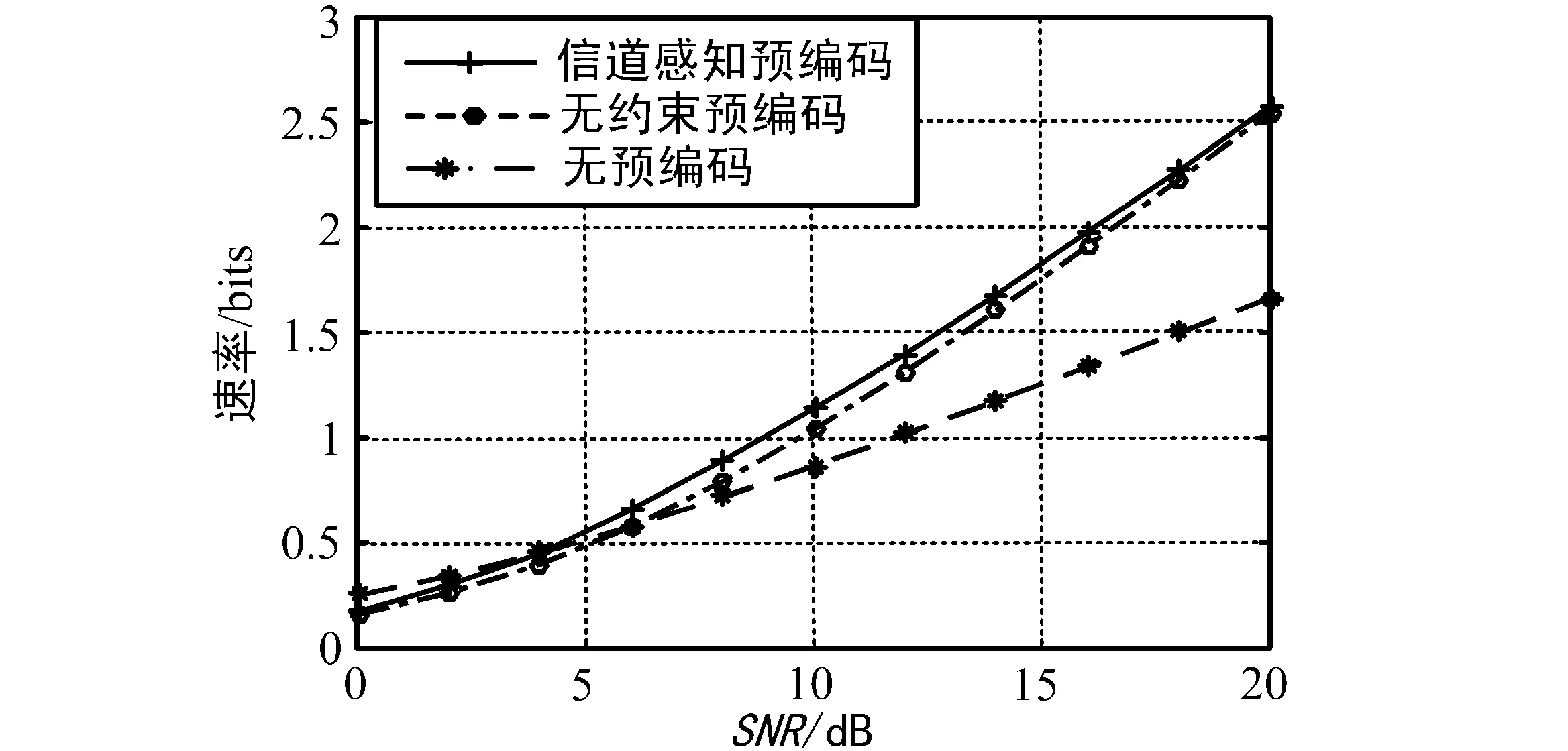
图4 衰落信道不同预编码方案的可达速率
3.4 仿真验证
此小节通过仿真验证对比以上3种中继方案的误码率性能。仿真中,两个源节点采用的格码为取自2,且每一维度的点数为2,等效于4-QAM星座。在中继节点处,中继通过格译码得到源节点发射码字的整合线性组合。图5给出了不同方案下的误符号率。
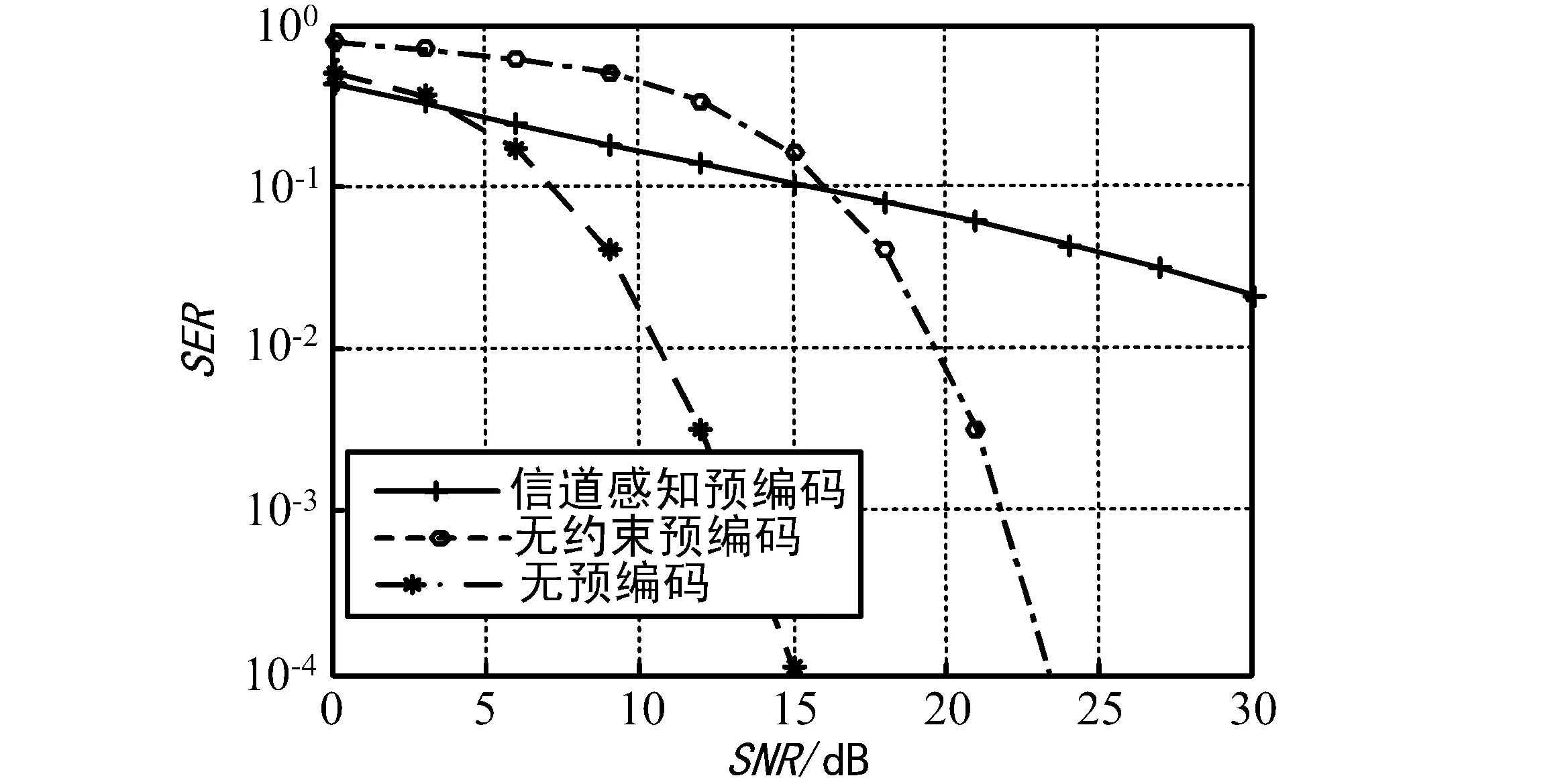
图5 衰落信道不同预编码方案的误符号率
从仿真结果可知,当SNR大于特定值时(以上仿真条件中约4.0dB),执行信道感知预编码的中继方案其性能优于没有预编码的中继方案。而执行无约束预编码的中继方案只在SNR高于约16.5dB时的性能好于无预编码的中继方案。
实际上,当信道状态过于恶劣时,能够正确译码的概率将十分小,因此当信道状态较好时再传输便会得到一定增益,信道感知预编码中继方案的性能提升即来源于此。这一思想也类似于常见的注水算法[10]。
4 结束语
对于双向中继通信来说,无论是AWGN信道还是衰落信道,计算-转发策略都是非常合适的中继策略。从可达速率的表达式可知,基于计算-转发策略的传输方案总是能够达到最大自由度,并不需要一般化多源、多中继网络中的限制条件[11]。针对衰落信道,提出了信道感知的预编码方案,能够进一步提升该信道下的可达速率,本文研究为推动物理层网络编码技术的实际应用提供了有意义的参考。
[1]NazerB,GastparM.ReliablePhysicalLayerNetworkCoding[J].ProceedingsoftheIEEE,2011,99(3):438-460.
[2]LiewSC,ZhangS,LuL.Physical-LayerNetworkCoding:Tutorial,Survey,andBeyond[J].PhysicalCommunication,2013,6:4-42.
[3]AhlswedeR,CaiN,LiS-YR,etal.NetworkInformationFlow[J].IEEETransactionsonInformationTheory,2000,46(4):1204-1216.
[4] Zhang S,Liew S C,Lam P P.Hot Topic:Physical-Layer Network Coding[C]∥ Proc.ACM Int.Conf.Mobile Comput.Netw.(MobiCom),Los Angeles,CA,2006:358-365.
[5] Popovski P,Yomo H.The Anti-Packets Can Increase the Achievable Throughput of a Wireless Multi-Hop Network [C] ∥ Proc.IEEE Int.Conf.Commun.(ICC),Istanbul,Turkey,2006:3885-3890.
[6] Katti S,Gollakota S,Katabi D.Embracing Wireless Interference:Analog Network Coding[C] ∥ ACM SIGCOMM Computer Communication Review,2007,37(4):397-408.
[7] Nazer B,Gastpar M.Compute-and-Forward:Harnessing Interference Through Structured Codes[J].IEEE Transactions on Information Theory,2011,57(10):6463-6486.
[8] 李 博.物理层网络编码及其在非对称双向中继通信中的性能研究[D].哈尔滨:哈尔滨工业大学,2013:14-30.
[9] Feng C,Silva D,Kschischang F R.An Algebraic Approach to Physical-Layer Network Coding[J].IEEE Transactions on Information Theory,2013,59(11):7576-7596.
[10]Tse D,Viswanath P.Fundamentals of Wireless Communication[M].New York:Cambridge University Press,2005.183-185.
[11]Wang R,Liu E,Liu Y.Achievable Degrees of Freedom of Cellular Multiuser Two-Way Relay Networks[J].IEEE Transactions on Vehicular Technology,2014,63(8):4028-4038.
New Scheme of Two-way Relay Communication Based on Compute-and-Forward
WANG Hai-long1,WANG Gang1,YAN Ze-tao2
(1.Communication Research Center,Harbin Institute of Technology,Harbin Heilongjiang 150001,China;2.Shenzhen Academy of Aerospace Technology,Shenzhen Guangdong 518057,China)
Compute-and-forward-based physical layer network coding (PNC) scheme is investigated for wireless two-way relay channel.The achievable rates are derived both for AWGN channel and fading channel.To achieve a higher transmission rate for fading channel,a new transmission scheme using channel inversion precoding is proposed.It is revealed that,with the proposed channel-aware precoding scheme,the communication performance can be improved enormously.For two-way relay channel,the scheme based on compute-and-forward can achieve the maximum degree of freedom,which indicates that compute-and-forward is the most suitable relaying scheme for two-way relay channel.
compute-and-forward;two-way relay;physical layer network coding;lattice codes;precoding
10.3969/j.issn.1003-3114.2016.06.08
王海龙,王 钢,闫泽涛.基于计算-转发策略的双向中继通信方案[J].无线电通信技术,2016,42(6):33-36,44.
2016-07-18
国家重点基础研究发展计划(2013CB329003)
王海龙(1988—),男,博士研究生,主要研究方向:物理层网络编码、5G关键技术。王 钢(1962—),男,教授,博士生导师,主要研究方向:信源信道编码、物理层网络编码。
TN919.23
A
1003-3114(2016)06-33-4
