“数学思想”在教学中的演绎
2016-12-20江苏盐城市大丰区南翔实验小学224100朱兴安
江苏盐城市大丰区南翔实验小学(224100) 朱兴安
“数学思想”在教学中的演绎
江苏盐城市大丰区南翔实验小学(224100) 朱兴安
“数学思想”是人们在对数学长期认知探索的过程中获取的精华,是提高学生数学能力和思维品质的核心理论。教师可以从符号思想、类比思想、建模思想三个方面着手,选择适应小学生年龄特点的教学内容,深入浅出、寓教于乐地让学生主动参与、自主探究,切实提高学生对数学思想的领悟,有效提升学生的数学文化素养。
小学数学 符号思想 类比思想 建模思想 演绎
在小学数学教学中渗透数学思想,有利于学生对数学概念、公式、定理的深入理解和灵活运用,有利于学生掌握符号思想、类比思想、建模思想等诸多数学思想,实现从知识的传授到能力的培养,使学生在掌握知识的基础上学会分析问题、解决问题,是贯彻课程教学理念,提升学生数学素养的重要途径。
一、符号思想,具体情境中总结规律
数学就是符号加逻辑,其中符号包括字母、数字、图形和各种特定的符号,它为数学思想的交流提供了便利,消除了语言的障碍。学生的符号感可以帮助其快速从具体情境中找出数量关系和变化规律,并利用符号简洁、准确地表达出来,有效避免了语言上的含糊性和歧义性,进而通过符号之间的转化实现对问题的解决。
比如,在教学“乘法分配律”时,教师可以建立一定的问题情境,让学生讨论不同的计算方法,并在解决问题中寻找规律。教师出示题目:“在服装店里,一件上衣的价格为175元,一条裤子的价格为75元,买四套这样的衣服需要多少钱?”学生通过讨论列出(175+75)×4和175×4+75×4两种算式,这两种算式都对吗?学生积极地进行思考、计算,最终认为这两种算式都正确,可以用等号连接,于是便得出了(175+75)×4=175×4+75×4的结论。在进行几个相关的练习之后,学生掌握了类似算式的计算方法,总结出(a+b)×c=a×c+b×c。
学生利用a、b、c来代表不同数字的方法就是符号思想的体现,简洁、准确地将数据实例集为一体,便于记忆和应用。在符号思想的领悟和学习中,学生深刻体会到了符号的实用性和优越性。
二、类比思想,对比辨析中迁移知识
“类比思想”是指当学生看到陌生问题中似曾相识的部分时,依据数学对象之间的相似性,将数学知识迁移,从而将表面复杂陌生的问题直接化、简单化,以帮助学生打开思路,利用已有的知识经验找出问题的切入点,最终创造性地解决问题。类比思想不是简单的生搬硬套,需要进行一定的抽象分析,这就需要教师的及时点拨和学生的灵活运用。
比如,有这样一道应用题:“星期天小明一家去登山。上山时,每小时行3千米,下山时,每小时行5千米,除去休息和游玩的时间,小明一家上下山花费的总时间为5个小时,全程共行了19千米。问上山和下山的路程各是多少千米?”在讨论中,不少学生将这道题看成了一个行程问题,在不用方程的基础上,学生较难得出答案。然而,这道题的实质是典型的“鸡兔同笼”问题的变化,可以这样来解决:假设上山时间为5小时,则小明一家所走的路程为3×5=15(千米),比实际行程少了19-15=4(千米),这是因为把下山的时间当做了上山的时间,故下山所用的时间为4÷(5-3)=2(小时),从而可以得到上山路程为3×(5-2)=9(千米),下山路程为5×2=10(千米)。
数学中还有许多定理都是类比思想的直接反映,如长方形面积与三角形面积、圆柱体积与圆锥体积等,只要学生领悟了蕴含在其中的类比思想,对公式的记忆就更为扎实和准确,更能激发学生的创造力。
三、建模思想,实践操作中构建知网
“建模思想”是人们对数学现象的一种概括,利用抽象的数学模型来模拟实际生活中的数学现象,使学生学会如何将实际问题简化,并将其转化为一个数学问题,进而从数学的角度来解决。建模思想的融入提升了学生的应用意识与实践能力,促进了学生对数学知识与技能的综合运用,能够使学生快速找出知识之间的连接点,形成科学致密的知识网络。
例如,在复习“平面图形面积”时,教师可以让学生计算教室内存在的平面图形的面积,从而建立一个平面求积的数学模型。在对教室的观察中,学生需要求出长方形、正方形、三角形、梯形、圆形的面积,通过相互之间的讨论,学生逐步掌握了这些图形面积的求法,并以长方形为基础建立了数学模型。(如下图所示)
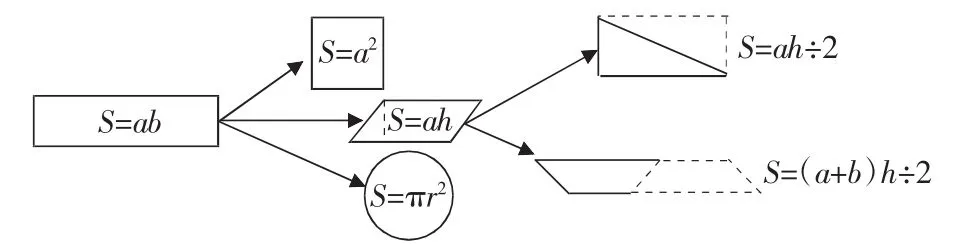
通过对平面图形的探索,学生经历了“问题情境—模型构建—分类求解—实际应用”四个过程,改变了单一的记忆、接受和模仿的学习方法,有效促进学生参与实践、思考探究,真实了解了建模思想。
当然,数学思想在小学数学教学中的渗透,不仅仅是要培养学生的思维能力,也要注重对其情感素养的熏陶,强调在学习知识、技能和方法的同时,注重学生情感的积极体验,激发学生平稳、持续的学习动力。
(责编 李琪琦)
G623.5
A
1007-9068(2016)35-084
