“等号”
——学生学习方程的“脚手架”
2016-12-20浙江常山育才小学324200聂茂林
浙江常山育才小学(324200) 聂茂林
“等号”
——学生学习方程的“脚手架”
浙江常山育才小学(324200) 聂茂林
在小学数学教学中,方程占有非常重要的地位,对丰富学生解决问题的策略、提高学生解决问题的能力、发展学生的数学素养有着非常重要的作用和意义。小学作为方程教学的起始阶段,引导学生认识方程的特征、感受到方程的优点及能写出方程,是教师教学的首要任务。在课堂教学中,教师要抓住方程中的“等号”,引导学生找出等量关系,让方程教学变得更有效。
方程 等号 脚手架 数形结合 天平 等量关系
学生从小学四年级开始学习方程,这是学生由算术思维向代数思维发展的新起点。方程体现其关系的就是符号“=”,既表示结果,又表示相等关系。从方程与等号的实质来看,方程用等号将左右两边联系起来,说明等号的左右两边等价。因此,学生要学好方程,“等号”就是一个很好的“脚手架”。
北师大版小学数学教材四年级下册“认识方程”一课是学生正式接触方程的起始课,本课教学在学生日后学习等式的性质、解方程及运用方程解决简单的实际问题的过程中起着承上启下的作用。那么,课堂教学中,教师应如何帮助学生利用好“等号”这个“脚手架”学习方程呢?我做了以下尝试。
一、以天平为载体,初识方程
在之前的数学学习中,学生对利用数与数之间的关系列出算式已经有很深刻的认识了。那么,初次接触方程,学生的陌生感如何消除?如何从等式中引出方程?同时,我发现学生在生活中对天平还是有所了解的,而且天平能够很形象地表示出左右两边的相等关系——两边平衡,也就是表示左右两边相等。
于是,我在课的一开始,用天平(如下图)导入,引出等式和不等式,使学生明白天平平衡时,左右两边的质量是相等的,此时天平左右两边是等量的关系,可以用等号来表示此时的关系。接着变换天平左右两边的物品(已知质量与未知质量),学生就能够很容易用未知数来代替未知质量的物品,从而引出方程,这样学生对方程的接受也就顺理成章了。这样教学,不仅让学生在已有知识与经验的基础上经历等式的变化过程,为学生学习方程提供了良好的表象支撑,而且轻松地消除了学生对方程的陌生感,使学生很快就接纳了方程这一新知识。
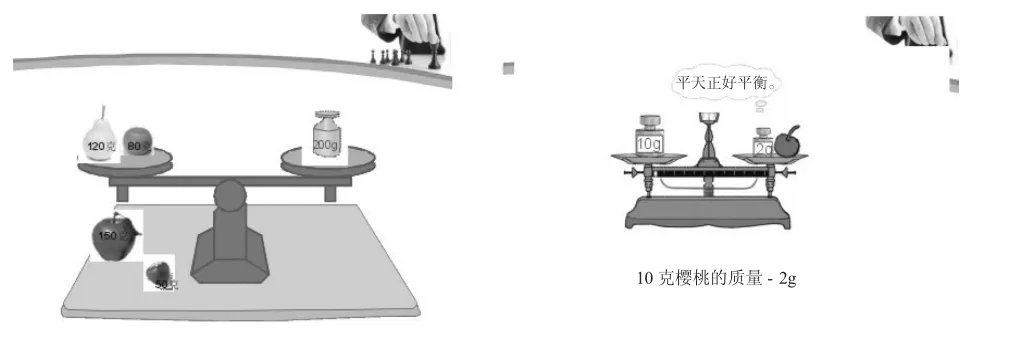
二、抓住等量关系,列出方程
列方程解决实际问题的关键是寻找等量关系,这是方程教学的重点,也是学生学习的难点。例如,教学“邮票的张数”一课时,在课前进行的前测中,我发现学生对于找等量关系存在着一定的困难。而且,我在以往的教学中也发现用方程解决稍复杂的问题时,学生常常不知道怎么列方程,究其原因是学生不能正确地找出问题中的等量关系。基于上述问题,北师大新版小学数学教材在“认识方程”一课前增加了“等量关系”这一内容。所以,教师一定要清楚地认识到“等量关系”这一内容的重要性,并将找等量关系贯彻整个教学过程。只要学生能准确地找出等量关系,即找到那个“=”,就为正确地列出方程打下坚实的基础。
因此,在课堂教学中,我从以下几方面入手,对学生加强等量关系的渗透与训练。
1.抓住关键词句找等量
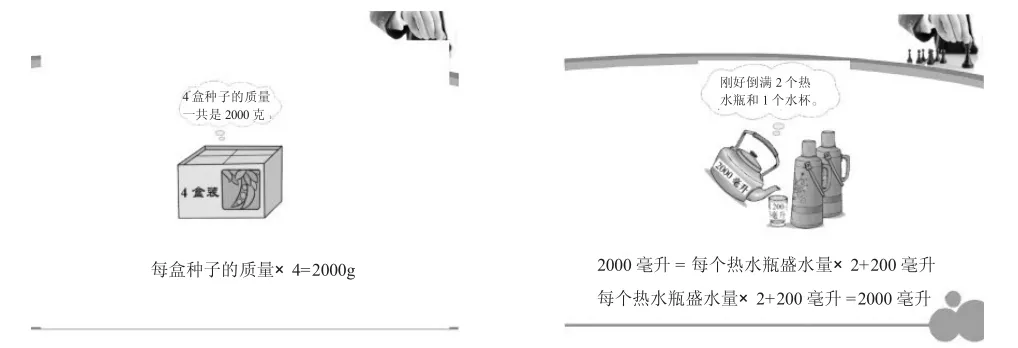
如上图所示,第一幅图中的“一共”清楚地告诉我们“4盒种子的质量=2000克”,进而可以得到“每盒种子的质量×4=2000g”这一等量关系;而第二幅图中的“刚好倒满”,说明了“2000毫升=每个热水瓶盛水量×2+200毫升”,即每个热水瓶盛水量×2+200毫升=2000毫升。另外,在应用题的表述中,一般都会有关键句、关键词,如“比……多……”“……是……的几倍”等句子,我们也称之为题眼,抓住题目中的“题眼”,就能使题目中的等量关系明朗化。
2.利用数形结合找等量
几何直观是小学数学的十大核心素养之一,而数形结合是小学阶段最常见的一种问题解决策略。学生在感知应用题情境的基础上画出示意图,采用数形结合的方法分析数量关系,可使问题变得直观明了,更容易解决问题。
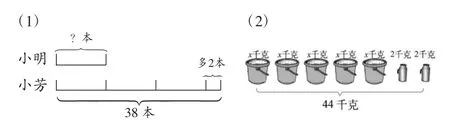
课堂上,我在出示上图后,让学生说说图意,找出题中的等量关系。同时,在学生看图的过程中,我加强训练学生用文字语言来表达题中等量关系的能力。这样通过“以数辅形”,使学生易于理解题意,更好地解决问题,为后面学习“以形辅数”打好基础。经常进行这样的练习,可以在数与形之间架起沟通的桥梁,提高学生解决问题的能力。
此外,在更多的时候,“形”要为“数”服务。如有这样一道题:“姐姐和弟弟一共有180张邮票,姐姐的邮票张数是弟弟的3倍。姐弟俩分别有多少张邮票?”在这道题中,姐姐和弟弟两人的邮票张数之间的关系比较复杂,如何找到题目中的“=”呢?教师应有意识地利用数形结合这一思想方法,引导学生把隐藏在题中的等量关系用图画出来,使题中的等量关系变得更清晰。如下图:
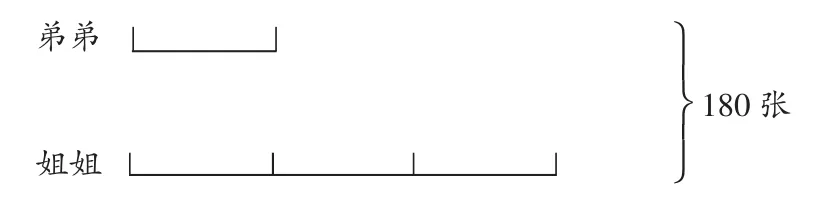
从图中就能直观地看出“弟弟的邮票张数+姐姐的邮票张数=180张”和“弟弟的邮票张数×3=姐姐的邮票张数”这两个等量关系,这样在后面方程教学中再遇到类似的问题时,学生便能驾轻就熟,正确地找到题中的数量关系,从而列出方程求解。
正如苏霍姆林斯基所言:“教会学生把应用题画出来,其用意就在于保证由具体思维向抽象思维过渡。”数形结合让示意图成为思维的载体,使列方程所必需的条件同时呈现在视野内,而直观地看见比在脑海中想象要容易些,失误也会减少,从而使方程教学收到了事半功倍的效果。
3.在动态变化中找等量
在教学过程中,我发现学生根据天平来找等量关系还是比较容易的,学生完成得也较好,但是过渡到寻找动态变化的量之间的等量关系时,学生就产生了学习障碍。于是在第二次上课时,我让学生在脑中想象一个天平,在天平两边分别进行物体数量的增减变化,通过天平两边平衡来找等量关系,最终正确解决问题。
如有这样一道题:“书架上层的图书本数是下层的3倍,从上层拿30本到下层后,两层的图书一样多。书架上下层原来各有多少本图书?”出示题目后,我先让学生找出题中的“天平”——“书架上层的图书本数=书架下层的图书本数×3”,再在“天平”两边分别“-30本”“+30本”,这时候天平两边一样多,从而找到等价关系,得出“书架上层的图书本数-30=书架下层的图书本数+30”这一等量关系,最后根据关系式设未知数,从而轻易地解决了问题。
三、通过解决问题,突显优势
很多学生对于方程学习的印象是繁琐,主要原因有以下两个方面:一是用方程解决问题的步骤很复杂,不仅要设未知数,而且解方程的过程很麻烦,还要检验;二是感觉列方程时找等量关系比较复杂。那么,教师在教学中如何让学生感受到方程的优势,从一开始就接受方程呢?最好的方法,就是在学生初识方程时,让他们体会到用方程解决问题的优势。于是,我在教学中安排了以下的问题。
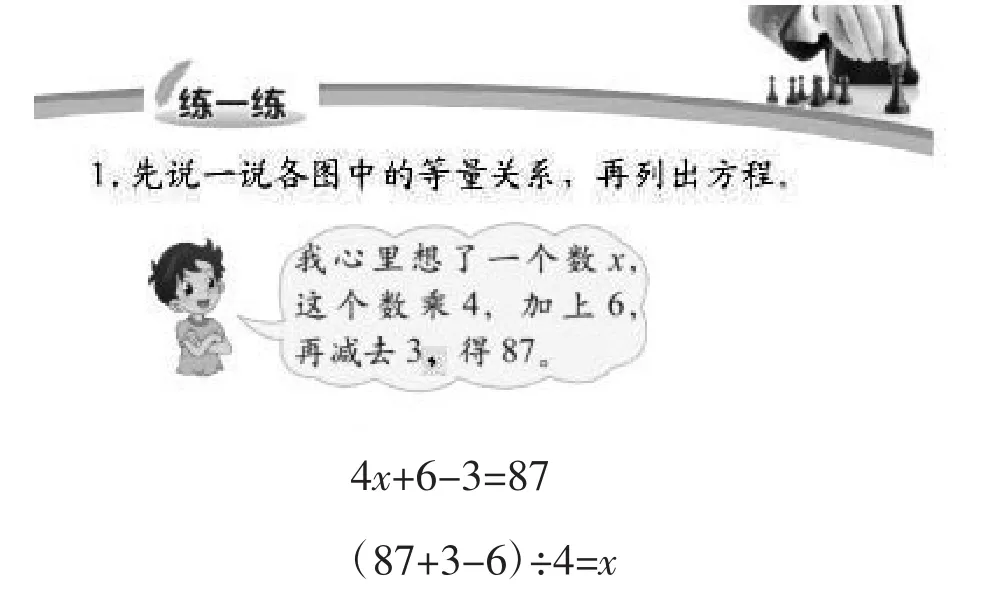
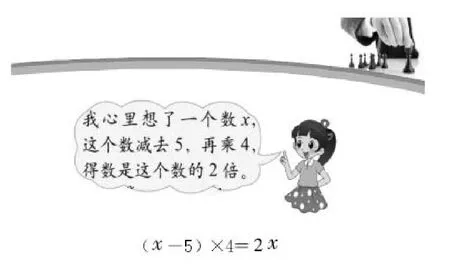
在解决第一个问题时,用算术法能轻易解决,但是到了第二题,再用算术法解决,明显有些吃力了。这时,学生发现找出题中数量间的等量关系,用方程能很快地列出算式,进而解决问题。这样方程的优势就很明显地体现出来了,学生也懂得再遇到此类题目时,不再绕弯子去列算式,而会用方程解决问题。学生感受到方程的优越性,心里对方程的接受度就明显提高了。在接下来的方程学习中,学生对方程的兴趣肯定会更高,学习效果也一定会有所提高。
方程作为小学数学的教学内容,虽然比重不大,但从认识方程开始,强调用数学符号“=”把要说的话表达出来是根本,是学生学好方程的“脚手架”。因此,课堂教学中,教师应引导学生经历方程从现实生活到数学结论的提炼过程,使学生懂得用数学符号提炼现实生活中的特定关系。同时,教师要抓住“等号”这个“脚手架”,引导学生找出题中的等量关系,让方程教学变得更简单、更有效。
(责编 蓝 天)
G623.5
A
1007-9068(2016)35-015
