调频振子-液体联合水平减振的流固耦合机理研究

郭涛,管志成,孙光普,李国君

(西安交通大学热流科学与工程教育部重点实验室,710049,西安)



调频振子-液体联合水平减振的流固耦合机理研究

郭涛,管志成,孙光普,李国君

(西安交通大学热流科学与工程教育部重点实验室,710049,西安)

为了解决晃荡液体在大幅值的水平加速度激励下不再具有稳定自由晃荡频率且无法满足调频条件而导致减振能力明显下降的问题,提出了一种将调频振子置入晃荡液体中构成联合系统的减振方法。采用分离求解隐式耦合的方法对忽略结构阻尼的联合系统衰减结构振动进行了数值模拟,计算结果表明,联合系统能够在保持振子共振吸能的基础上充分利用液体晃荡对振动能量进行耗散,具有优于单纯调频质量减振或晃荡液体减振的性能。联合系统在液体晃荡时的减振作用优于液体无法晃荡时的情况;液体自由晃荡频率远离振动频率有助于振子保持共振吸能能力。在共振的容器中和振子的激励下液体晃荡具有强烈的耗能作用,这是联合系统减振的主要机理。根据这一机理,在保证振子共振和增强液体耗能作用的思路下对联合系统进行了优化,优化后联合系统即使忽略结构阻尼,阻尼比也可达到5.6%。

调频振子;晃荡液体;水平减振;流固耦合;数值模拟

部分充液容器发生简谐振动时,若内部的液体具有与容器振动频率相同的自由晃荡频率,则液体能够通过调频共振效应快速地从容器振动中吸收能量,并利用波浪碰撞、黏性耗散等消耗能量,实现容器及其关联结构的被动减振,该类装置称之为调频液体阻尼器(TLD)。Fujino等人率先采用实验的方法系统地研究了TLD,总结出浅水TLD理论及减振模型[1-4]。早期单纯使用水作为减振介质的TLD抑振能力有限,于是内置隔网[5-6]、水平短板[7-8]、重泥水[9]、多模态并联[10]、多缝屏[11]、超浅水[12]等技术先后用于改善液体的耗能能力。

TLD的基本理论与调频质量减振器(turned mass damper,TMD)相似,实践中TMD需要合适的阻尼,以便在共振效应被破坏前快速消耗能量。相比TMD,TLD设置简单,其驻波频率通过改变水深进行调节且容易被微弱振动激发,而且自身具备耗能作用等优势[13]。但是,当结构振动对液体水平激励的加速度幅值过大时,TLD中液体的自由晃荡频率不再是驻波频率和稳定值,液体也无法与振动结构发生共振,此时晃荡液体对此类振动的抑制能力有限[14]。为增强晃荡液体在非调频情况下的减振效果,本文提出调频振子与晃荡液体联合减振系统(简称联合系统),即在晃荡液体中浸入一个固有频率与激励频率相同的弹簧振子,利用调频振子来增强减振系统吸能的作用,该系统结构见图1。

图1 调频振子与晃荡液体联合减振系统

图1中,调频振子浸入在晃荡减振器的液体之中,既与晃荡液体相互影响,又与晃荡减振器并联在振动系统上。该系统类似于汪正兴提出的振子-液体双调频减振方法[15],但液体无需满足调频条件。本文采用分离求解器隐式耦合的方法模拟了调频振子-液体联合减振器对水平振动的衰减作用,从而验证了该系统的有效性。

1 物理模型与数值方法

1.1 物理模型

待减振结构为外壁边长100 mm、壁厚5 mm的正方体钢制封闭容器,其质量约为2.127 4 kg。容器侧壁与刚度为8 398.6 N/m的水平弹簧的一端连接,弹簧的另一端固定。在容器腔内置入一个20 mm×20 mm×80 mm的钢制振子,质量为0.251 2 kg,钢块与容器侧壁面用刚度为991.7 N/m的水平弹簧连接。容器内充水至50%高度处,水质量约为0.332 kg,水面没过振子顶部25 mm。弹簧振子的角频率

(1)

式中:K为弹簧刚度系数;mS为振子质量。容器与振子均具有10 Hz的固有频率,使得振子能够与容器发生共振。若忽略容器的激励以及浸入液体中的振子,液体的驻波角频率

(2)

式中:B、d分别为容器宽度、液体深度;g为重力加速度。容器内液体的驻波频率为2.82 Hz,认为其偏离了结构振动频率。由于联合系统通过振子调频共振来实现减振,所以该系统减振性能依赖于振子、晃荡液体的固有频率与振动频率的关系,而对结构尺寸并不敏感,因此本文对上述联合减振模型的研究具有一般性,其结论对实际工程问题同样适用。

1.2 数值计算方法

联合系统的内部液体在容器的带动下发生受迫晃荡,而调频振子在共振效应与容器进行快速的能量交换的同时,与液体发生相互作用,整个减振过程是一个复杂的流固耦合过程。本文使用商用软件Ansys Workbench实现了流、固物理域的分离求解和隐式耦合,并对减振过程进行了模拟[14],其中:固体域用Mechanical模块按有限元法求解了基于虚功原理的单元平衡方程矩阵;流体域用CFX模块按有限体积法求解了雷诺时均Navier-Stokes方程;在一个时间步内,两个求解器在流固交界面上多次传递流体压力与结构位移的计算结果,以完成边界条件的更新,达到计算收敛,满足隐式计算的精度。

固体域的计算网格见图2。容器与振子只具有水平方向的平移自由度,容器内表面与振子外表面均为流固耦合界面,弹簧的质量、阻尼及结构间的接触摩擦忽略。流体域中,固体、空气与液体的自由交界面采用连续表面张力模型计算,并根据网格单元的体积权重进行界面光顺;振子运动产生的网格变形使用位移扩散模型求解;湍流模型采用均化的标准κ-ε模型;计算精度为双精度,以避免自由表面曲率计算时存在较大的舍入误差;耦合时间步长为0.002 s;其他计算设置详见文献[14]。

图2 容器、振子的计算网格及弹簧连接示意

1.3 计算方法验证

使用文献[8]中通过调频晃荡液体抑制4根柔性梁支撑的质量块振动的实验对上述的数值方法进行了验证。原实验中,振动质量块约27.9 kg,由4根22 mm×3.5 mm×390 mm的柔性钢柱支撑,其自由振动频率约为2.5 Hz。质量块上的长方体容器尺寸为130 mm×210 mm×200 mm,容器内水深100 mm,驻波频率约为2.3 Hz。质量块的初始水平位移为1.30 mm±0.05 mm,激励后质量块自由振动,且带动容器中的液体晃荡。调频液体起初从质量振动中吸收能量,来加剧自身晃荡、衰减振动,随后晃荡液体会将能量返还给质量块,反过来带动质量块振动。该响应过程的实验结果与本文数值方法得到的结果见图3。

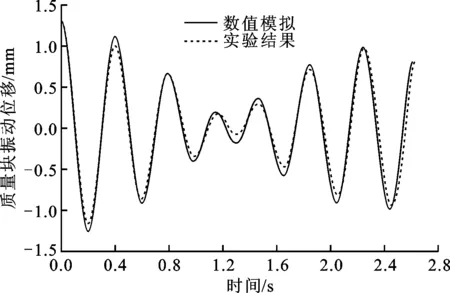
图3 调频液体减振过程的数值模拟与实验结果对比

图3中,质量块振动位移的数值解与实验数据吻合良好,说明数值方法成功地预测了TLD与质量块之间的能量传递过程和微弱耗散的耦合过程,且可用于液体晃荡减振过程中的流固耦合分析。

2 数值计算结果及分析

2.1 联合系统的减振性能

容器在初始振幅为5 mm的自由水平上进行振动,同时调频振子、晃荡液体、联合减振系统3种减振方式对容器振动进行了抑制,由此得到的0.6 s内容器的响应曲线见图4。

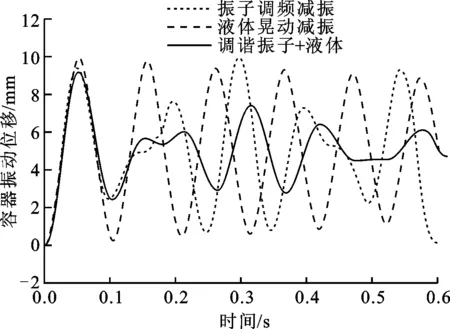
图4 3种减振方式下的振动抑制效果对比

图4中:使用调频振子减振的容器响应曲线在0.15、0.45 s时幅值最小,在0.3、0.6 s附近达到峰值,这是由于忽略了结构自身的耗能阻尼后,能量仅在振子与容器间往复传播却没有耗散的缘故,说明TMD减振虽具有良好的吸能作用,但未考虑耗能的作用;使用液体晃荡减振的容器位移曲线幅值缓慢衰减,表现出晃荡对容器振动的强伴随性,吸能与耗能的表现均很差,等效阻尼比仅为0.81%;使用联合减振的容器位移曲线具有先衰减后增强的特征,在0.3、0.6 s附近波峰幅值相较前2种方式均具有较大程度的衰减,等效阻尼比达到3.1%,说明联合系统能够有效地结合调频振子的吸能作用和晃荡液体的耗能作用。

为在0.6 s时达到相似的阻尼效果,需要TMD阻尼比达到7%。阻尼比为7%的TMD在抑制相同振动的过程中容器与振子的位移响应及其与联合系统减振的对比见图5。

图5中:TMD在0.48 s后的振动位移相位已经与容器相同,说明TMD此时丧失了与容器位移相差π/2相位(共振吸能时振子滞后容器π/2相位,共振放能时振子领先容器π/2相位)的调频共振功能,失去了高效抑振的能力;联合系统的振子调频能力减弱,但并未完全消失,而在0.9 s容器仍能与振子保持约0.4 π的相位差并被振子激励振动,在1 s时的减振效果略优于TMD。这说明联合系统中的耗能作用与TMD阻尼并不相同,其在相似的耗能作用下对振子调频能力的破坏更小,另外联合系统同样可以通过添加TMD阻尼来增强耗能作用。

(a)阻尼比为7%时的TMD减振

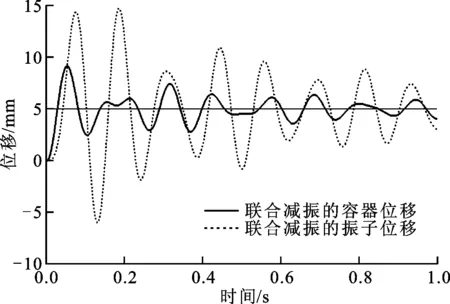
(b)TMD-液体联合减振图5 2种减振方式下容器与振子的位移响应

2.2 联合系统的减振机理

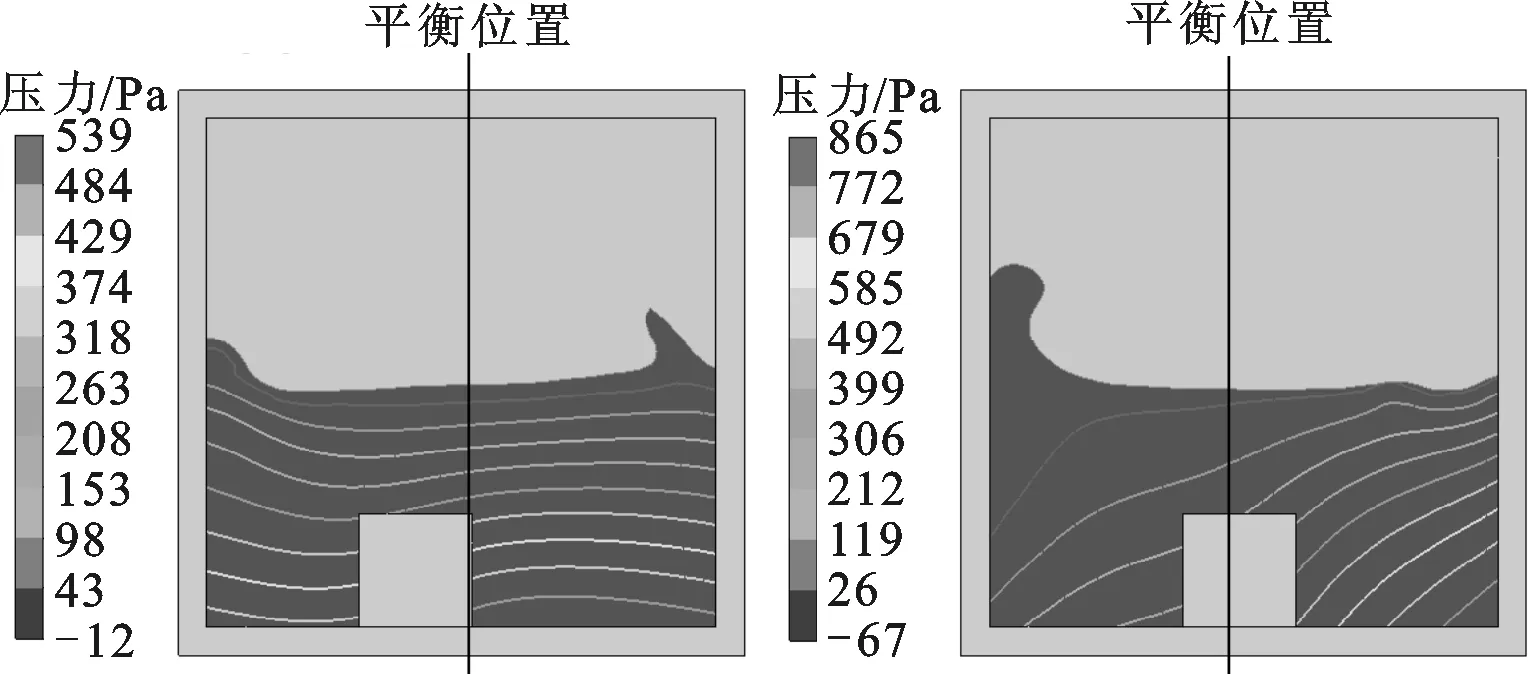
抑制容器振动的初期联合系统的振子或容器在具有最大振幅的几个时刻点上容器内的两相分布与液体压力场分布见图6。

图6中:在0 s,容器尚静止于初始振幅并具有左(正)向运动的趋势,容器内振子、液体对容器的作用力为0;在0.052 5、0.075、0.105、0.130、0.185、0.240、0.315 s,容器的速度大小和方向分别为静止(速度值较小)、右(反)向、静止、左向、静止、右向、静止,而振子对容器的作用力的大小和方向分别为无作用(作用力值较小)、左向、无作用、右向、左向、右向、无作用,液体压力对容器的作用力大小和方向分别为左向、无作用、右向、左向、右向、左向、左向,整个过程中振子先吸能后放能,致使容器振幅出现图5b中先衰减后增强的结果,但最大幅值明显减小。振子与晃荡液体的能量均来自容器振动,多数情况下液体总是阻碍容器或结构运动,造成总机械能耗散。

(a)0 s (b)0.052 5 s

(c)0.075 s (d)0.105 s

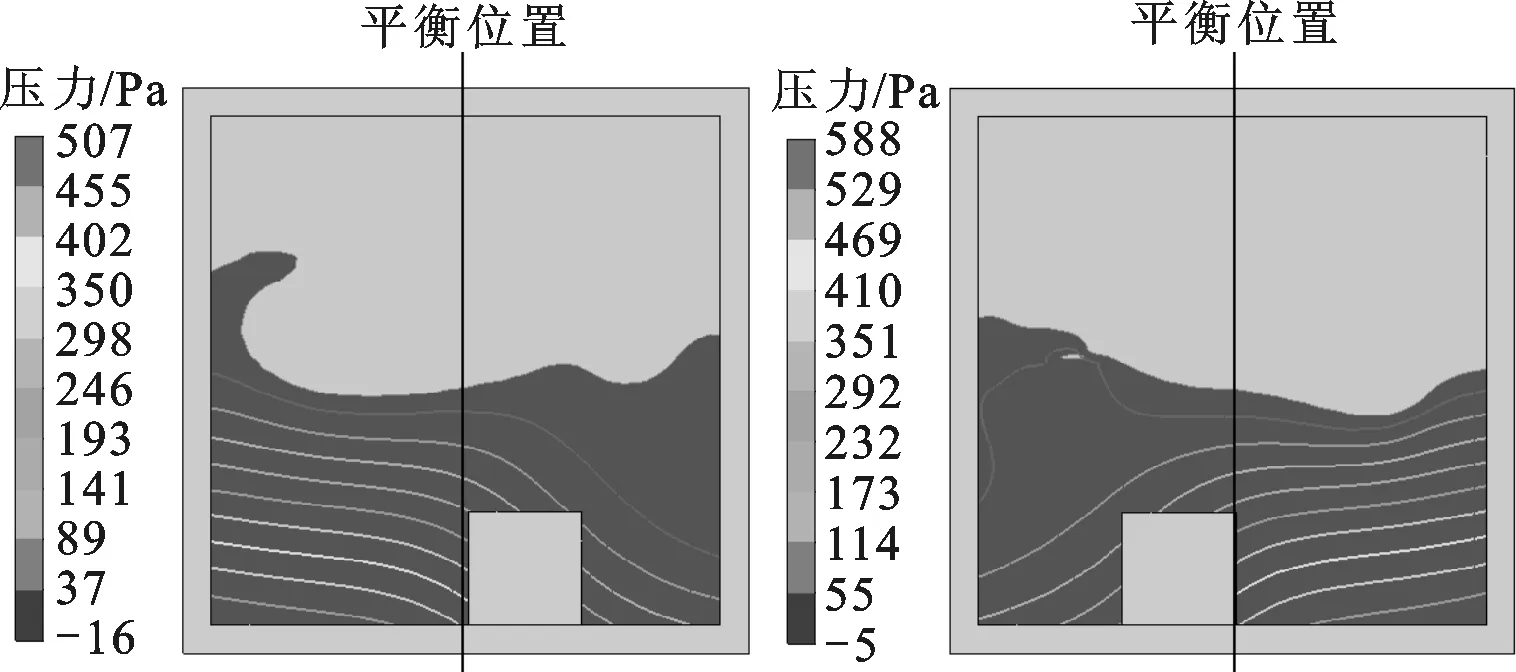
(e)0.130 s (f)0.185 s

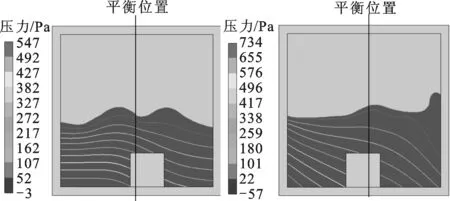
(g)0.240 s (h)0.315 s图6 联合减振系统下容器内两相分布与液体压力分布

在减振过程中,联合系统的容器振动使液体发生受迫晃荡,而调频振子与容器发生共振运动,且带动周围液体伴随运动,液体在2种不同相位的激励下引发不同相位的波浪,并在不断碰撞壁面的同时发生黏性耗散。为考察液体晃荡在联合系统中的作用,将调频振子置入容器后通过充满水形成100%充液的减振系统。多种充液比下联合系统的减振能力见图7。图7中,容器的振幅衰减随充液比的增加而减小。50%充液容器的抑振效果最好,振子的吸能效果最强;100%充液容器的衰减最慢,从中难以观察到振子与容器的能量交换。这说明随着充液比的增加,液体发生晃荡难度越大,100%充液时无晃荡,此时液体耗能作用仅来源于液体与结构相对运动的碰撞及湍流黏性的耗散作用,不存在波浪碰撞与破浪破碎的耗能作用。随着充液比的增加,液体的晃荡能力逐渐减小,直至消失,这增强了振子刚性,破坏了振子的调频能力。可见,液体的晃荡增强了联合系统的减振性能。

图7 多种充液比下联合系统减振性能对比

为考察液体调频条件对联合系统性能的影响,通过改变容器与振子的弹簧刚度系数将容器与振子的固有频率修改为2.82 Hz,使得激励加速度峰值降低为1.57 m/s2,或者通过重力加速度将液体驻波频率修改为10 Hz,使得水平加速度的数值小于重力加速度的数值,这样容器在自由振动时振子与液体同时满足调频条件。联合系统的振子与液体同时满足调频条件时的减振性能见图8。

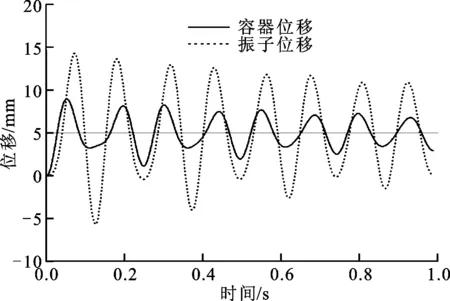
(a)调节弹簧刚度使振子、液体的调频均为2.82 Hz

(b)调节重力加速度使振子、液体的调频均为10 Hz 图8 振子与液体同时满足调频条件时联合系统的减振性能

图8a联合系统的减振能力低于图8b,原因是在低加速度激励下液体的晃荡、碰撞等耗能效应较差。2种调频下的减振性能均不如液体未调频时的情况,大约在5个振动周期后振子振动相位基本与容器保持一致,调频共振的能力消失,此后的联合系统的减振效果明显减弱。

联合系统中调频振子不仅与液体并联在振动结构上,还与晃荡液体串联。由振子耦合的动力学分析可知,质量相似且固有频率同为ωS的双振子串联所组成的耦合系统将具有一对固有频率,即

(3)

双振子各自的自由振动是以ω1、ω2简谐振动的叠加,当振子质量相似且首级振子的质量或刚度远大于次级振子时,双振子将近似具有各自原本的自由频率。

由上述可见:振子与液体串联且满足调频条件时,振子的固有频率会发生变化,此时振子无法与振动结构保持共振,从而造成联合系统的减振能力下降;振子与液体的质量相似,而液体驻波频率明显小于振子固有频率时,液体刚度远小于振子,此时液体中振子能够与容器发生共振,液体的晃荡受到振子与容器2种相同频率却不同相位的振动的激励,以阻碍容器或振子运动,促使波浪碰撞、破碎、强剪切流动及湍流运动发生,致使能量在液体、振子和容器三者之间的往复传递中不断耗散,从而保证了联合系统的减振能力。

2.3 联合系统的优化策略

在联合系统的减振过程中,耗能作用是将振动最终被消除,吸能作用是振动在前期快速衰减、耗能得到有效发挥。在调频振子具有共振吸能作用的基础上,尽量增强联合系统的耗能效应便可提高联合系统减振能力。联合减振过程中容器受到内部振子与液体的作用力见图9。

图9 联合系统减振中液体、振子对容器的作用力

图9中,振子作用力幅值明显大于液体作用力,说明振子对容器的影响更大,这是振子调频共振的基础。结合图5b和图6知,振子作用力由振子相对于容器的位移决定,液体对容器作用力的相位由容器初始位移相位决定,而振幅则受容器位移幅值影响较大。该作用力在振子激励容器振动时起阻碍作用,也是液体耗散的重要表现形式。在保持共振作用力为主的基础上,适度增加液体作用力的比例,例如增加液体黏性、适当增加液体质量或减小振子质量等,有助于提高系统的减振能力。

振子质量为1.6 kg、液体为1000#硅油的联合系统容器的响应与原系统对比见图10。图10中,优化后等效阻尼比达到5.6%,减振性能提升了约80%,证明了本文优化思路的正确性。影响联合系统减振能力的其他因素以及其他优化思路还需要进一步研究和讨论。

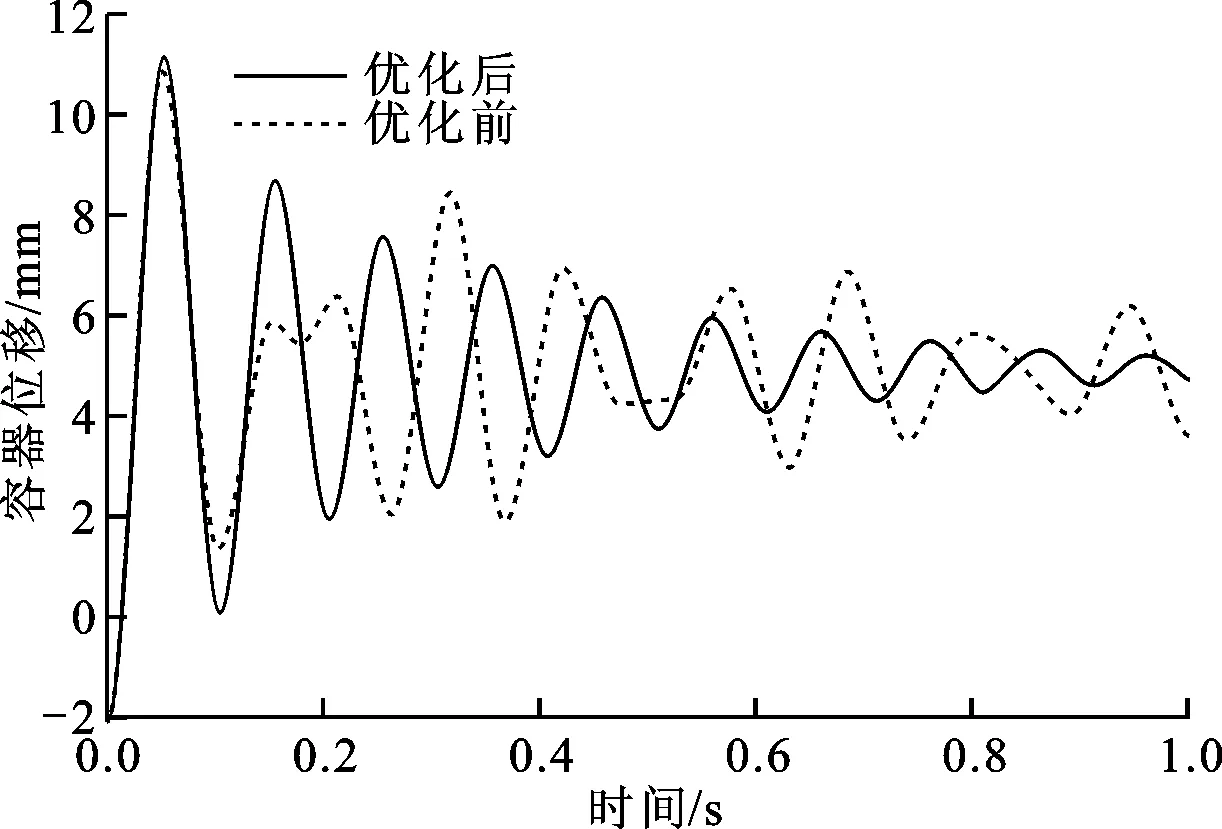
图10 优化前后联合系统对振动容器的抑制能力对比

3 结 论

本文提出了调频振子-液体联合减振方法,并对联合系统减振的流固耦合过程进行了数值模拟,分析了联合系统具有减振能力的内在机理及其优化策略,由此得到如下结论。

(1)无阻尼TMD振子与容器中内置50%的水组成的联合系统可以给模型容器提供3.1%的等效阻尼比,其减振能力相当于阻尼比为7%的TMD,且不会破坏振子的调频特性。联合系统结合了TMD与晃荡液体的优势,具有优于两者的减振能力。

(2)TMD-液体联合系统本质上是串、并联并存的减振系统,当振子的固有频率与激励频率近似,液体的驻波频率远小于激励频率时,调频振子具有共振吸能的能力。液体受容器作用而剧烈晃荡并与振子发生碰撞,是液体能量耗散的主要方式,充液比过大会影响液体的晃荡而降低系统的减振性能。

(3)TMD-液体联合系统减振时,振子对容器的作用力足够大才使得晃荡液体不会破坏振子与容器的共振关系,而液体作用力是液体耗散能量的保证,优化后的联合系统应当在不破坏振子作用力为主导的基础上提高液体作用力。适当减小振子质量、更换黏性工质可以增加液体的作用力,使模型系统的等效阻尼比提高5.6%。

对于单一简谐振动的抑制能力,联合系统优于TMD和TLD,对于地震等多激励频率下的振动能否如TMD与TLD那样采用多个不同频率减振器并联的方式实现减振,尚有待于进一步研究。

[1] FUJINO Y, PACHECO B M, CHAISERI P, et al. Parametric studies on tuned liquid damper (TLD) using circular containers by free-oscillation experiments [J]. JSCE Struct Eng/Earthquake Eng, 1988, 5(2): 381-391.

[2] SUN L M, FUJINO Y, PACHECO B M, et al. Nonlinear waves and dynamic pressures in rectangular tuned liquid damper (TLD): simulation and experimental verification [J]. JSCE Struct Eng/Earthquake Eng, 1989, 6(2): 251-262.

[3] FUJINO Y, SUN L, PACHECO B M, et al. Tuned liquid damper (TLD) for suppressing horizontal motion of structures [J]. Journal of Engineering Mechanics, 1992, 118(10): 2017-2030.

[4] SUN L, FUJINO Y, KOGA K. A model of tuned liquid damper for suppressing pitching motions of structures [J]. Earthquake Engineering & Structural Dynamics, 1995, 24(5): 625-636.

[5] KANEKO S, YOSHIDA O. Modeling of deep water type rectangular tuned liquid damper with submerged nets [C]∥ASME Pressure Vessels & Piping Division Conference. New York, USA: ASME, 1994: 31-42.

[6] KANEKO S, YOSHIDA O. Modeling of deepwater-type rectangular tuned liquid damper with submerged nets [J]. ASME Journal of Pressure Vessel Technology, 1999, 121(4): 413-422.

[7] ANDERSON J, SEMERCIGIL S, TURAN Ö. An improved standing-wave-type sloshing absorber [J]. Journal of Sound and Vibration, 2000, 235(4): 702-710.

[8] ANDERSON J, SEMERCIGIL S, TURAN Ö. A standing-wave-type sloshing absorber to control transient oscillations [J]. Journal of Sound and Vibration, 2000, 232(5): 839-856.

[9] SUN L, KILUCHI T, GOTO Y, et al. Tuned liquid damper (TLD) using heavy mud [J]. WIT Transactions on the Built Environment, 1998, 38: SM980081.

[10]HONG-NAN L, YING J, SU-YAN W. Theoretical and experimental studies on reduction for multi-modal seismic responses of high-rise structures by tuned liquid dampers [J]. Journal of Vibration and Control, 2004, 10(7): 1041-1056.

[11]TAIT M J, EI DAMATTY A A, ISYUMOV N, et al. Numerical flow models to simulate tuned liquid dampers (TLD) with slat screens [J]. Journal of Fluids and Structures, 2005, 20(8): 1007-1023.

[12]MARSH A, PRAKASH M, SEMERCIGIL E, et al. A shallow-depth sloshing absorber for structural control [J]. Journal of Fluids and Structures, 2010, 26(5): 780-792.

[13]文永奎, 孙利民. 大跨度斜拉桥钢塔施工阶段制振用TMD、TLD装置及其性能试验 [J]. 地震工程与工程振动, 2008, 28(3): 157-164. WEN Yongkui, SUN Limin. TMD, TLD and performance tests for vibration control of steel tower of large span cable-stayed bridge during construction [J]. Earthquake Engineering and Engineering Vibration, 2008, 28(3): 157-164.

[14]郭涛, 李国君. 内嵌晃荡液体减振的流固耦合分析 [J]. 西安交通大学学报, 2014, 48(9): 117-122. GUO Tao, LI Guojun. Fluid-structure interaction analysis for vibration suppression of interior sloshing liquid [J]. Journal of Xi’an Jiaotong University, 2014, 48(9): 117-122.

[15]汪正兴, 王波, 钟继卫, 等. 液体质量双调谐减振器(TLMD)研究与应用 [J]. 桥梁建设, 2011(1): 10-13. WANG Zhengxing, WANG Bo, ZHONG Jiwei, et al. Research and application of tuned liquid and mass damper (TLMD) [J]. Bridge Construction, 2011(1): 10-13.

[本刊相关文献链接]

郭涛,李国君.内嵌晃荡液体减振的流固耦合分析.2014,48(9):117-122.[doi:10.7652/xjtuxb201409020]

韩宾,文灿,于渤,等.泡沫填充波纹夹芯梁的面内压缩破坏模式分析.2014,48(11):37-43.[doi:10.7652/xjtuxb201411 007]

毛阳,陈志勇,史文库,等.磁流变液双质量飞轮扭振减振特性研究.2014,48(6):127-133.[doi:10.7652/xjtuxb201406 022]

张超,陈天宁,王小鹏,等.颗粒阻尼线性离散元模型参数的选取方法.2014,48(3):96-101.[doi:10.7652/xjtuxb201403 018]

舒歌群,赵文龙,梁兴雨,等.约束阻尼结构的振动分析及结构参数优化研究.2014,48(3):108-114.[doi:10.7652/xjtuxb201403020]

王成,缑锦,白俊卿,等.利用主成分分析的模态参数识别.2013,47(11):97-104.[doi:10.7652/xjtuxb201311018]

刘石,仲继泽,冯永新,等.使用磁流变阻尼器的大型汽轮发电机定子端部绕组振动控制.2013,47(4):39-43.[doi:10.7652/xjtuxb201304008]

王建伟,徐晖,季聪,等.内嵌流体柔性板的流体自适应减振机理数值分析.2008,42(5):612-616.[doi:10.7652/xjtuxb 200805022]

(编辑 苗凌)

Fluid-Structure Interaction Analysis of Vibration Suppression by Tuned Oscillator-Liquid Combined System

GUO Tao,GUAN Zhicheng,SUN Guangpu,LI Guojun

(Key Laboratory of Thermo-Fluid Science and Engineering, Ministry of Education, Xi’an Jiaotong University, Xi’an 710049, China)

The ability of sloshing liquid to suppress vibration is weakened in the case of large motivating acceleration due to the inconstant free sloshing frequency. A combined system where a tuned spring oscillator is put into the sloshing liquid damper is presented. The vibration suppressing process of the structure with the combined system is numerically simulated with an implicit coupling approach of partitioned solvers. The results show that the combined system is endowed with greater ability to suppress vibration because of the dissipating effect of sloshing liquid as keeping the oscillator resonant absorbing ability. A large difference of the free frequencies between sloshing and oscillator is benefit to keep the tuned condition. The liquid sloshing is simultaneously motivated by resonant container and oscillator to enhance dissipating ability, which is considered as the main suppressing mechanism of the combined system. Following the frame that enhancing the liquid dissipating as keeping the oscillator tuned, the damping ratio even gets up to 5.6% in the optimized combined system without damping structure.

tuned oscillator; sloshing liquid; vibration suppression; fluid-structure interaction; numerical simulation

2015-03-10。 作者简介:郭涛(1984—),男,博士生;李国君(通信作者),男,教授,博士生导师。

时间:2015-10-23

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20151023.1103.006.html

10.7652/xjtuxb201601005

O328;TP391.9

A

0253-987X(2016)01-0028-06