基于多目标萤火虫算法的供应链生产效率与稳健性研究

舒 彤，高小琴，陈 收，汪寿阳，2

(1.湖南大学工商管理学院，长沙410082;2.中国科学院数学与系统科学研究院，北京100190)

基于多目标萤火虫算法的供应链生产效率与稳健性研究

舒 彤1，高小琴1，陈 收1，汪寿阳1，2

(1.湖南大学工商管理学院，长沙410082;2.中国科学院数学与系统科学研究院，北京100190)

文章针对供应链存在的不稳定性，运用情景规划法考虑不同种类的供应链中断。在供应链网络设计时考虑其稳健性，对供应链中断下的生产效率与稳健性进行权衡，并采用多目标萤火虫算法求解这个权衡问题，使结果具有连贯性。研究结果表明，目标函数最优时的总成本反而比供应链最有效时的总成本低，产生了成本优势，企业可以根据生产效率与稳健性权衡的近似帕累托前沿图选择合适的生产效率与稳健性以促进企业的持续发展。

供应链中断；多目标萤火虫算法；生产效率；稳健性

1 模型建立

对于供应链，以往文献大多只考虑一种产品和一个制造中心，如Aviral(2011)[1]所涉及的供应链。这种设计不太符合实际，这里设计多种产品、多个制造中心的供应链。大多数企业拥有生产产品的制造中心，把产品运往各地的配送中心和对产品有需求的客户区，这种三级供应链的模式也被诸多学者采用(Aviral，2011)[1]。因此这里设计了多种产品、多个制造中心的三级供应链，供应链包括位置固定的多产品制造中心a，潜在的配送中心b和位置固定的客户区c，如图1所示。

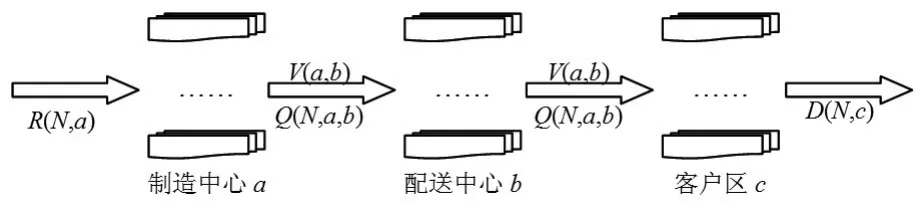
图1 多种产品多个制造中心的三级供应链

鉴于Magdalini(2014)[2]的数学模型，本文在供应链设计时引入供应链的稳健性，设计供应链节点和链接中断的混合整数线性规划模型如下。

1.1 参数设置

①索引

a:制造中心；b:配送中心；c:客户区；N:产品种类；s:情景集合

②决策变量

制造中心是否供应配送中心和配送中心是否供应客户区的二进制变量分别定义如下：

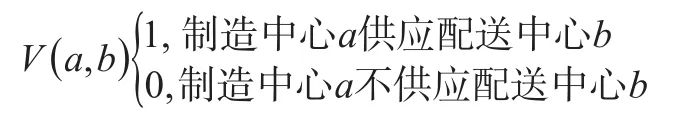
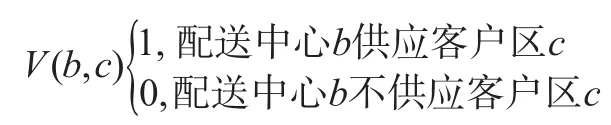
定义整数变量以描述多级供应链：

R(N，a):制造中心a生产产品N的数量；Q(N，a，b):从制造中心a到配送中心b产品N的数量；Q(N，b，c):从配送中心b到客户区c产品N的数量

③需求参数

D(N，c):客户区c对产品N的年需求量

④效率参数

ηe:供应链生产效率；ηr:供应链稳健性

⑤成本参数

c(b，f):建立配送中心b时，每年所摊销的固定成本；C(N，b，v):建立配送中心b时，每年摊销的产品N的单位变动成本；C(N，a):制造中心a生产每单位N产品的生产成本；C(N，b，h):配送中心b所发生的产品N的单位持有成本；C(N，a，b):每单位产品N从制造中心a到配送中心b的单位运输成本；C(N，b，c):每单位产品N从配送中心b到客户区c的单位运输成本；u(N):机会成本

⑥距离参数

G(a，b):从制造中心 a到配送中心 b的距离；H(b，c):从配送中心b到客户区c的距离

⑦概率参数

p(s):情景s发生的概率

⑧中断产品数量参数

q(N，s):情景s下N产品中断的数量

1.2 约束条件

①网络结构约束

制造中心、配送中心和客户区之间所有相关网络结构约束总结为：

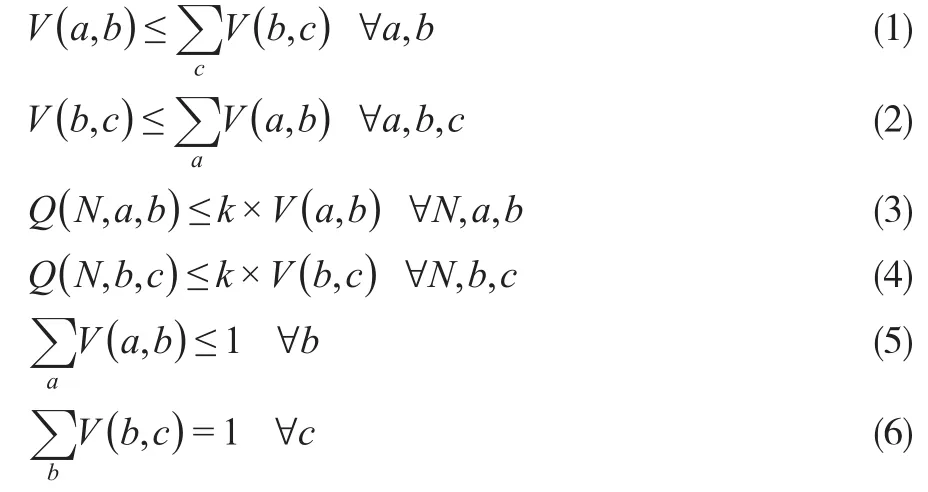
式(1)表示如果制造中心a服务配送中心b，那么配送中心b至少供应某个客户区。式(2)说明如果建立配送中心b，那么客户区c可能由配送中心b供应，也有可能不由配送中心b供应。只有当制造中心a供应配送中心b时，制造中心a才能提供产品N给配送中心b，因此有约束条件(3)，其中k是一个适当的大数，可令k=10，0000，0000。同样的约束条件可以应用到配送中心b和客户区c之间，如式(4)所示。式(5)和式(6)是单一来源约束，是为了确保每个配送中心和每个客户区分别只能由一个制造中心和一个配送中心供应。

②物料平衡约束

假设不存在库存积累或损耗，物料平衡约束总结为：

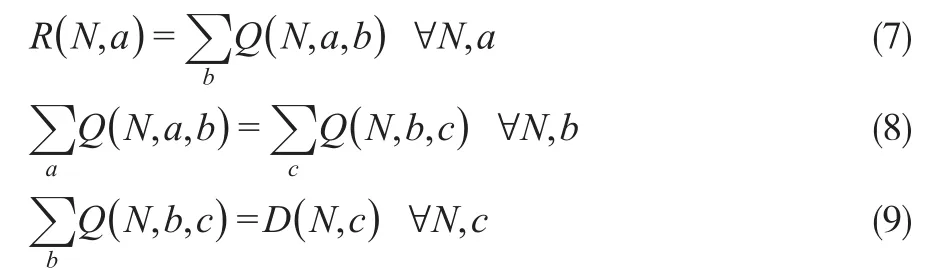
式(7)说明制造中心a提供给所有配送中心的产品N的数量应当等于制造中心a生产的产品N的数量。同样，制造中心提供给配送中心b的产品N的数量应当等于配送中心b提供给所有客户区的产品N的数量，如式(8)所示。式(9)是为了确保每个客服区的需求得到满足。

③非负约束

所有连续变量必须非负：

为有效缩减搜索空间，供应链生产效率和稳健性必须非负：

1.3 目标函数

供应链的建立既要考虑生产效率也要兼顾稳健性，因此目标函数设定为最大化供应链生产效率和最大化稳健性两个相互冲突的目标。供应链生产效率用运营成本来诠释，供应链稳健性用预期中断成本来诠释。

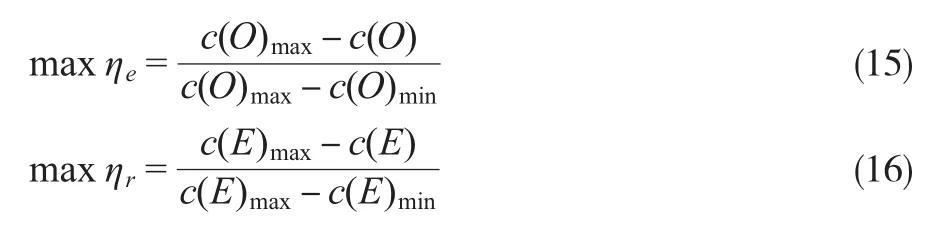
c(O)max:供应链最稳健下的运营成本；c(O)min:供应链最有效时的运营成本；c(E)min:供应链最稳健下的预期中断成本；c(E)max:供应链最有效时的预期中断成本。

目标函数中的运营成本包括基础设施成本、生产成本、配送中心的物料持有成本和运输成本。

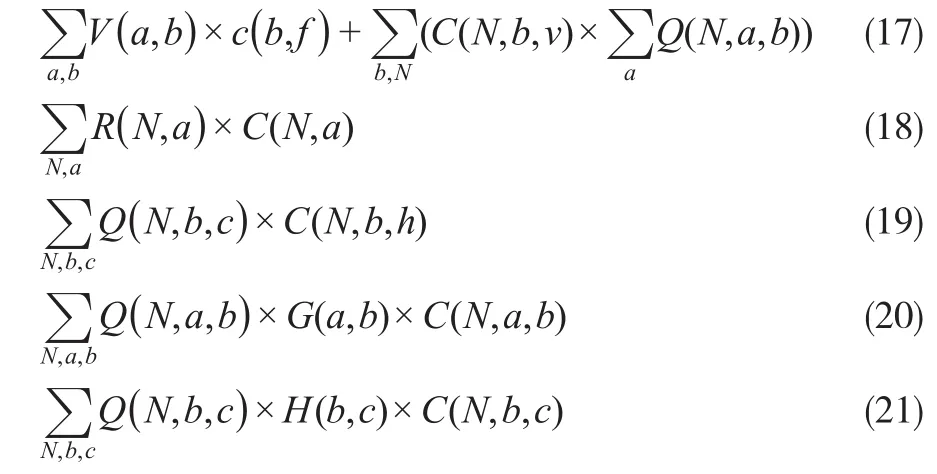
式(17)为基础设施成本，其之所以发生是由于配送中心的建立。这里假设配送中心的成本由固定成本和变动成本组成，其中固定成本是确定的，只要配送中心建立就存在，而变动成本则取决于配送中心产品N单位变动成本每年摊销额乘以数量。假定制造中心的生产成本以单位成本的速率与产品的产量成正比，制造中心的总生产成本如式(18)所示。式(19)表示配送中心的物料持有成本，其与配送中心发生的总吞吐量成正比。式(20)和式(21)分别表示制造中心到配送中心的运输成本和配送中心到客户区的运输成本，运输成本是产品数量、距离和单位运输成本的函数。一般情况下货车是满载货物行驶的，因此运输成本的规模经济效应在此忽略不计。

综上所述，运营成本的表达式为：

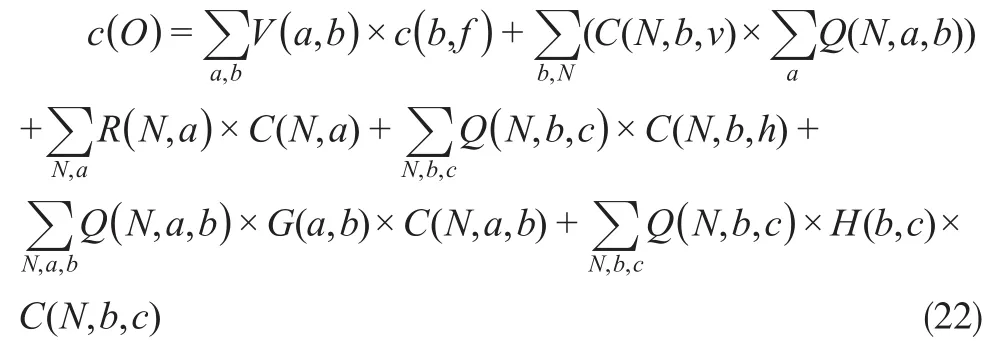
目标函数中的预期中断成本用情景法定义。情景法是一个古老的概念，从最早记录时间开始，人们就已经对未来很感兴趣并且把情景法作为间接探索未来社会和制度的工具(Bradfield，2005)[3]。本文采用情景规划法计算和分析供应链不同中断情景下发生的预期中断成本，情景分别设定为制造中心节点中断或配送中心节点中断和制造中心到配送中心的链接中断或配送中心到客户区的链接中断。预期中断成本用情景s发生的概率、情景s下N产品中断的数量和产品N的单位边际利润的乘积来表示：

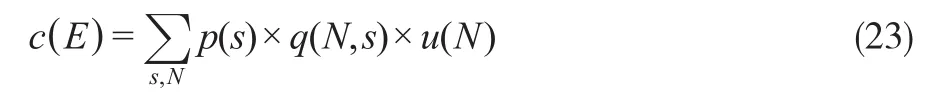
其中，p(s)为情景s发生的概率；u(N)是机会成本，即产品N的单位边际利润；q(N，s)为情景s下N产品中断的数量：

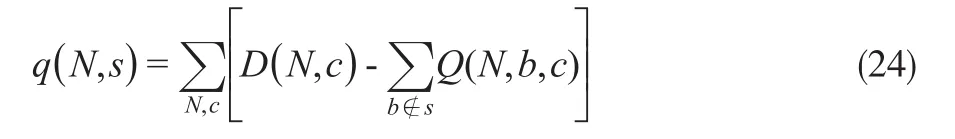
所以，预期中断成本的表达式为：

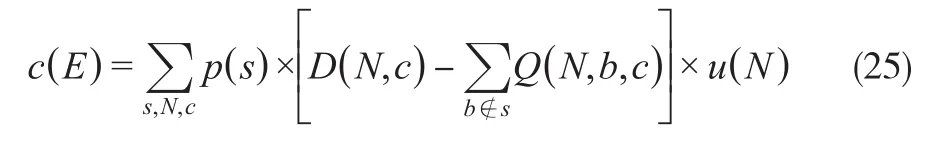
2 多目标萤火虫算法

多目标萤火虫算法可以同时考虑最大化供应链生产效率和最大化供应链稳健性两个相互冲突的目标，并且不同于单目标算法得出的离散点，可避免单目标算法陷入局部最优。

2.1 萤火虫算法

萤火虫算法是由Yang(2008-2014)提出并不断完善，是基于理想化的萤火虫闪烁行为特征：(1)萤火虫是雌雄皆宜的，所以萤火虫会吸引其他萤火虫而不管其性别是雌性还是雄性。(2)萤火虫的吸引度与其亮度成正比，并且随着距离的增加而减少。因此对于任何两个闪烁的萤火虫，不太亮的那个会向更亮的那个移动。如果对于一个特定的萤火虫，没有比其更亮的，那么这个萤火虫会随机移动；(3)萤火虫的亮度取决于目标函数的值[4-10]。

对于最大化问题，萤火虫的荧光亮度可以简单地设定为与目标函数值成正比。在萤火虫算法中，萤火虫的相对荧光亮度和吸引度都影响萤火虫的移动，这里需要对其进行定义。为简单起见，可以假设一个萤火虫的吸引度是由其荧光亮度决定的，而其荧光亮度又取决于目标函数。

然而，萤火虫的吸引度还和萤火虫之间的距离相关，随着距离的不同而不同，因此定义萤火虫的吸引度为：

其中，β0为r=0处的吸引度，即光源处的最大吸引度；γ表示光强吸收系数，用以模拟荧光在空中传播逐渐衰减的特性，可设为常数；rij为位置分别处于xi和xj的任意两个萤火虫i和j之间的笛卡尔距离，。值得注意的是，以上定义的r不局限于欧几里得距离，任何能有效解决优化问题的测量都可以作为距离r。

萤火虫i被亮度更高的萤火虫 j吸引并向 j移动时的位置更新定义为：

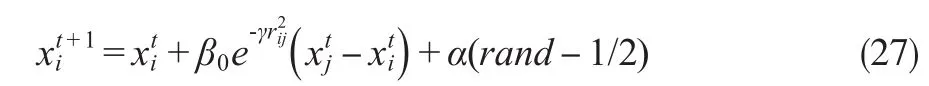
式中，α为步长因子，通常是常数；rand为[0，1]上服从均匀分布的随机因子；式中第二部分是吸引度所导致，第三部分为随机扰动项，为避免过早陷进局部最优解。

2.2 多目标萤火虫算法

对于多目标优化，一种方法是将所有的目标组合成一个单一目标，这样就可以使用单目标优化算法而不用太多修改。例如，Theofanis(2011)[11]以这种方式详细研究了直接使用萤火虫算法解决多目标优化问题。另一种方法是拓展萤火虫算法直接产生帕累托最优前沿，通过扩展萤火虫算法的基本思路，Yang(2013)[4]提出了多目标萤火虫算法。

多目标萤火虫算法的寻优过程是：首先定义目标函数；然后初始化萤火虫群，使其尽可能均匀分布在搜索空间，这可以通过使用抽样技术来实现；规定可容忍误差或最大迭代次数后，评估所有萤火虫的亮度或目标函数值并对每一对萤火虫进行比较；如果萤火虫 j支配萤火虫i，萤火虫i就按公式(27)向萤火虫j移动，移动之后如果i不满足约束条件，那么会重新生成一个萤火虫；如果一个萤火虫不受其他任何萤火虫支配，那么就把该萤火虫放入帕累托前沿，生成一个随机向量(之和等于1)，这样就可以获得一个最佳的组合解；接着非支配解集传递到下一次迭代；通过多次迭代，达到最大迭代次数后，一般可以得到近似帕累托前沿的n个非支配解集，从而实现寻优。

为更有效地随机移动，可通过最小化目标函数的加权和得到当前最优解，此时：

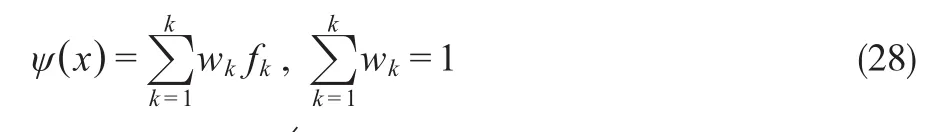
从帕累托前沿的角度来看，如果一只萤火虫没有受到其他萤火虫的支配，那么这只萤火虫移动的位置更新为：

综上所述，供应链中断下生产效率与稳健性权衡的多目标萤火虫算法流程如下。

步骤1：定义目标函数，初始化萤火虫群 xi(i=1，2，…，n)。

步骤3：通过非支配解更新拍累托前沿，记录最优解的个数，并把所有非支配解传递到下一次迭代，更新萤火虫的亮度和位置。

步骤4：重复步骤2，直到达到最大的迭代次数，得到全部帕累托最优解，找到当前最佳的近似帕累托前沿。

3 算例

为说明多目标萤火虫算法对多种产品多个制造中心的三级供应链混合整数线性规划模型的适用性，这里采用了一个位于中国的电脑制造公司。该公司生产多种产品，拥有多个制造中心和配送中心，符合多种产品、多个制造中心的三级供应链模型特征，因此用此算例来验证多目标萤火虫算法的适用性。该公司有两个位于发达城市的制造中心，即北京和上海。公司选择7个潜在的配送中心，分别位于华东、华南、华中、华北、西北、西南和东北地区交通最发达的省和直辖市，即北京、辽宁、上海、湖北、广东、四川和陕西。总共有33个客户区，包括香港和澳门在内的33个大陆省级行政区。

3.1 问题阐述

假设两个制造中心都能满足所有需求，并且都生产两种产品；一种为功能性产品：普通电脑，单位边际利润为200元；另一种为创新产品：新型电脑，单位边际利润为1300元。Fisher(1997)[12]根据产品的需求模式把产品分为两类：即功能性产品和创新产品。功能性产品需求可预测，产品生命周期长，边际贡献低；创新产品的需求量不可预测，产品生命周期短，边际贡献高。例如，盐、纸巾、牙刷等为功能性产品；新推出的汽车、时尚包等为创新产品。配送中心可以位于多达7个的潜在配送中心，最佳的配送中心位置由模型决定。制造中心、配送中心和客户区之间的距离用百度地图推荐路线计算。因为这项研究的重点是供应链节点中断和链接中断，因此这里假定客户区的需求是确定的，并且与客户区人口数成正比，省级行政区人口数根据《中国统计年鉴2013》得出[13]。

3.2 客户区需求

33个客户区对2种产品的年需求量如表1所示：普通电脑总的年需求量为135562台，新型电脑总的年需求量为13558台。

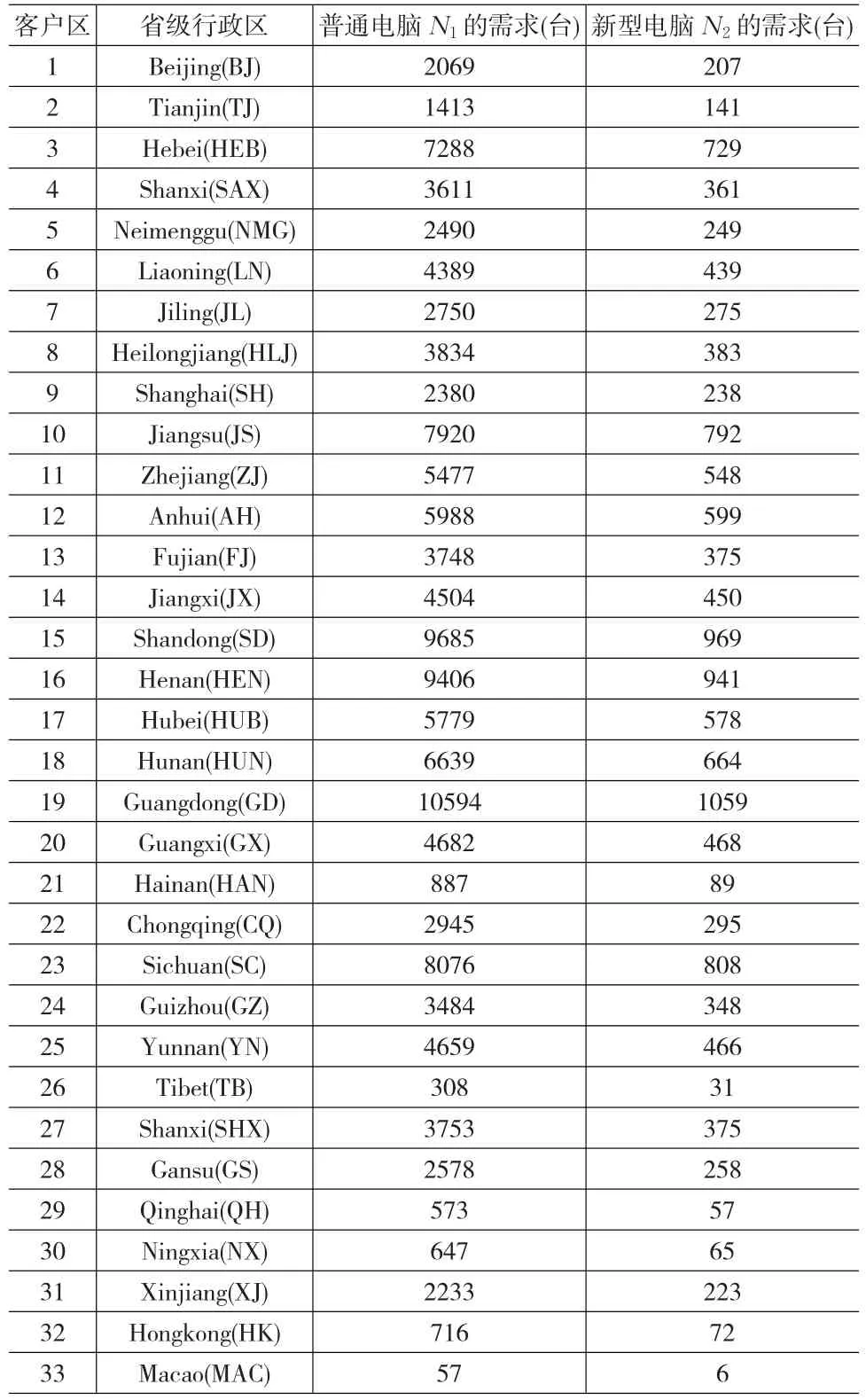
表1 客户区对功能性产品和创新产品的需求

3.3 制造中心、配送中心和客户区之间的距离

制造中心、配送中心和客户区之间的距离用百度地图推荐路线计算；从制造中心a到配送中心b的距离G(a，b)如表2所示，从配送中心b到客户区c的距离H(b，c)如表3所示。

表2 制造中心与配送中心之间的距离(千米)

表3 配送中心与客户区之间的距离(千米)

3.4 供应链中断概率

供应链中断可能由自然和人为因素造成，尽管自然灾害发生的概率难以量化，但是历史数据可用来预测自然灾害发生的概率。Li(2013)[14]用历史数据预测了未来自然灾害发生的概率。这里假定在政治局势稳定的中国，大多数供应链中断是由自然灾害引起。为得出中断的概率，这里采用《中国统计年鉴2013》中的分地区自然灾害损失情况来计算省级行政区发生自然灾害的相对概率[13]。制造中心和潜在配送中心中断的概率如表4所示。

表4 制造中心以及配送中心中断概率

3.5 相关成本

假设建立每个配送中心需要100000000元，且每个配送中心的使用年限为20年，因此建立配送中心时，固定成本每年所摊销的费用为500000元。建立配送中心时，普通电脑单位变动成本每年摊销费用为200元；新型电脑单位变动成本每年摊销费用为800元。制造中心生产每台普通电脑的生产成本都为2500元，制造中心生产每台新型电脑的生产成本都为6000元。每个配送中心发生的普通电脑的单位持有成本均为50元，新型电脑的单位持有成本都为100元。每台普通电脑和新型电脑从制造中心到配送中心的单位运输成本都为40元，从配送中心到客户区的单位运输成本也为40元。对应算例在Matlab R2014b中使用多目标萤火虫算法编程运行。

4 结果分析

供应链中断可能是节点中断，即配送中心中断，也可能是链接中断，即制造中心和配送中心之间的链接中断。这里对这两种情况都进行研究分析。

4.1 配送中心中断

由于配送中心位置相距很远，这里假定每个配送中心的中断是相互独立的并且多个配送中心的中断可同时发生。每个配送中心只有两种状态：正常运作或中断，并且假定配送中心中断就会失去所有容量。配送中心中断的概率取决于其所在的省级行政区，配送中心中断的概率如表5所示。配送中心可能发生一个中断，也可能多个中断同时发生。这里最多考虑三个同时中断，因为四个或四个以上配送中心同时中断的概率很小。该模型具有1586个约束条件、739个变量和种情景。

在运行模型之前，c(O)的上下界和c(E)的上下界必须计算。c(O)min直接通过最小化c(O)得出，c(E)在这一点就是最大值。c(E)min可以直接通过最小化c(E)计算，此时选出的仓库是最稳健的，通过选出的仓库求出此时的c(O)就是最大值。在配送中心中断情况下，c(O)和c(E)的界限值如表5所示。

表5 配送中心中断情况下c(O)和c(E)的界限值

模型使用多目标萤火虫算法进行仿真，通过200次迭代后，配送中心中断下最有效的供应链网络如图2所示。

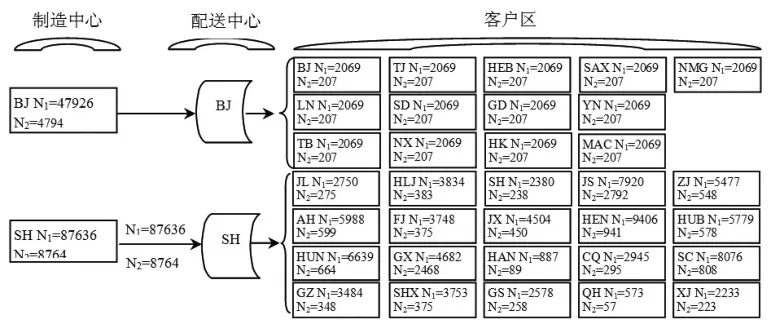
图2 配送中心中断下最有效的供应链网络

供应链最有效时的总成本(CO+CE)、最稳健时的总成本和目标函数最优时的最小总成本如表6所示。从表6可知，目标函数最优时的总成本反而比供应链最有效时的总成本低，这是由于目标函数最优时运营成本虽然增加了，但由此引起的预期中断成本的减少额度比运营成本的增加额度要多。在市场竞争日益激烈的当今，成本降低会给企业带来竞争优势。目标函数最优总成本最小时的供应链网络如图3所示。对比图2和图3可知，北京配送中心转移了一部分产品到湖北配送中心，由湖北配送中心配送，这是由于湖北配送中心的中断概率比北京的中断概率小所致。

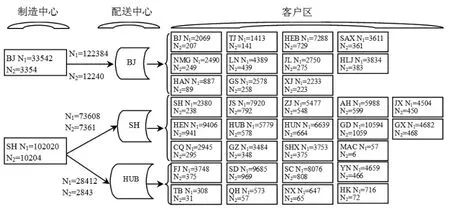
图3 配送中心中断下目标函数最优时的供应链网络

使用多目标萤火虫算法，经过200次迭代，获得近似帕累托前沿，如图4所示，横轴表示供应链生产效率，纵轴表示供应链稳健性。从图4可知，供应链稳健性随供应链生产效率的增加而减小，企业可根据所处产业性质和自身情况选择合适的供应链生产效率和稳健性。比如，容易受自然灾害影响的产业可适当提高供应链稳健性，对自然灾害不太敏感的产业可加大对生产效率的重视。

4.2 制造中心和配送中心之间的链接中断

图4 配送中心中断下生产效率和稳健性权衡的多目标帕累托前沿

链接是两个节点之间的链接，因此假定链接中断的概率为所连接节点中断概率的平均值，制造中心和配送中心之间的链接中断概率如表7所示。制造中心和配送中心之间的链接可能是一条中断，也可能多条同时中断，因为三条或三条以上链接中断的概率很小。为避免问题过于复杂，这里最多考虑两条同时中断。该模型具有1586个约束条件、739个变量和种情景。

表7 制造中心和配送中心之间的链接中断概率

在运行模型之前，c(O)的上下界和c(E)的上下界必须计算。c(O)min直接通过最小化c(O)得出，c(E)在这一点就是最大值。c(E)min可以直接通过最小化c(E)计算，此时的c(O)就是最大值。在制造中心和配送中心之间链接中断这种情况下，c(O)和c(E)的界限值如表8所示。

表8 制造中心和配送中心链接中断情况下c(O)和c(E)的界限值

模型使用多目标萤火虫算法进行仿真，通过200次迭代后，制造中心和配送中心链接中断下最有效的供应链网络和目标函数最优总成本最小时的供应链网络分别如图5和图6所示。对比图5和图6可知，北京配送中心转移了一部分产品到上海和陕西配送中心，由上海和陕西配送中心配送，这是由于上海和陕西配送中心的中断概率比北京的中断概率小所导致的。

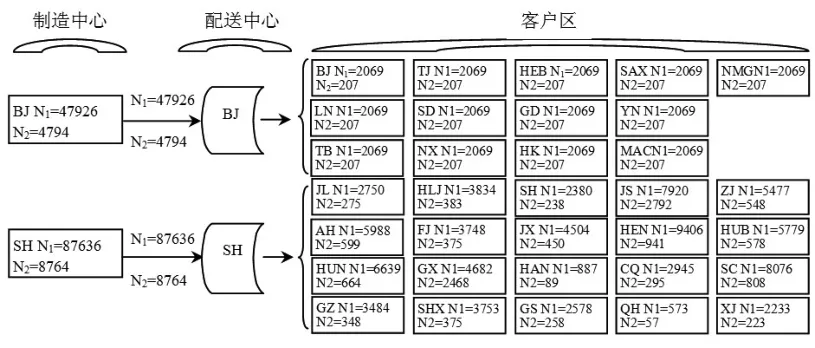
图5 制造中心和配送中心之间的链接中断下最有效的供应链网络

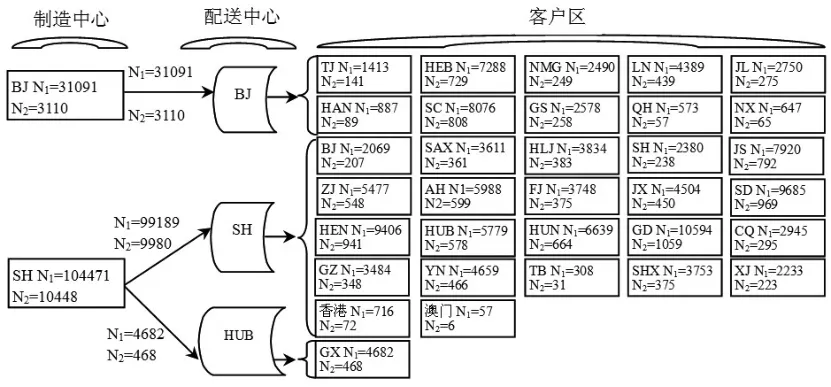
图6 制造中心和配送中心中断下目标函数最优时的供应链网络

使用多目标萤火虫算法，经过200次迭代，获得近似帕累托前沿，如图7所示，横轴表示供应链生产效率，纵轴表示供应链稳健性。从图4和图7可知，无论节点中断还是链接中断，供应链稳健性都随供应链生产效率的增加而减小。根据图7，企业可以对供应链生产效率和稳健性进行权衡，考虑所处内部环境和外部环境选择合适的供应链生产效率和稳健性。

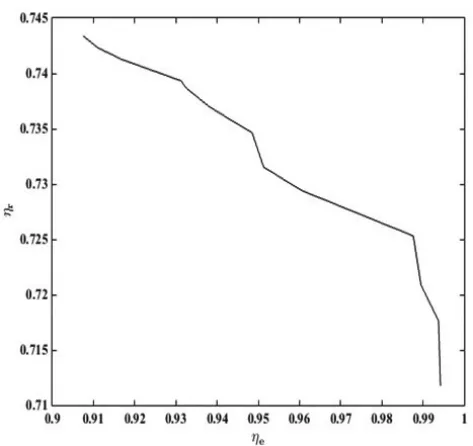
图7 链接中断下生产效率和稳健性权衡的的多目标帕累托前沿

5 结论

从多种产品多个制造中心的三级供应链混合整数线性规划模型的算例可知，无论是节点中断还是链接中断，供应链稳健性随供应链生产效率的增加而减小，而企业既希望提升生产效率又希望提升稳健性，但这两者此消彼长，所以必须对供应链中断下的生产效率和稳健性进行权衡，使目标函数最优。由仿真结果可知，目标函数最优时的总成本反而比供应链最有效时的总成本低，所以目标函数最优时的近似帕累托前沿给企业提供了选择合适供应链生产效率和稳健性的依据。总的来说，这种方法可以给供应链规划决策提供定量化工具。

[1]Shukla A，Lalit V A，Venkatasubramanian.Optimizing Efficiency-ro⁃bustness Trade-offs in Supply Chain Design under Uncertainty due to Disruptions[J].Physical Distribution and Logistics Management， 2011，41(6).

[2]Kalaitzidou M A，Longinidis P，Tsiakis P，et al.Optimal Design of Mul⁃tiechelon Supply Chain Networks With Generalized Production and Warehousing Nodes[J].Industrial and Engineering Chemistry Re⁃search，2014，53(33).

[3]Fielda R B，Wright G，Burt G，et al.The Origins and Evolution of Sce⁃nario Techniques in Long Range Business Planning[J].Futures，2005， 37(8).

[4]Yang X.Multiobjective Firefly Algorithm for Continuous Optimization [J].Engineering with Computers，2013，29(2).

[5]Yang X.Firefly Algorithms for Multimodal Optimization[C].Berlin: Springer，2009.

[6]Yang X.Firefly Algorithm，Lévy Flights and Global Optimization[C]. London:Springer，2010.

[7]Yang X，Deb.Eagle Strategy Using Lévy Walk and Firefly Algorithms for Stochastic Optimization[J].Studies in Computational Intelligence， 2010，284.

[8]Yang X.Firefly Algorithm，Stochastic Test Functions and Design Opti⁃misation[J].International Journal of Bio-inspired Compution，2012，2 (2).

[9]Yang X.Nature-Inspired Mateheuristic Algorithms:Success and New Challenges[J].Computer Engineering and Information Technology， 2012，1(1):1-3

[10]Yang X，Hosseini，Gandomi Amir Hossein.Firefly Algorithm for Solving Non-convex Economic Dispatch Problems With Valve Load⁃ing Effect[J].Applied Soft Computing，2012，12(3).

[11]Apostolopoulos T，Vlachos A.Application of the Fire fly Algorithm for Solving the Economic Emissions Load Dispatch Problem[J].Inter⁃national Journal of Combinatorics，Article ID 523806，2011.

[12]Marshall L.Fisher.What is the right supply chain for your product? [J].Harvard Business Review，1997，3(4).

[13]2013年中国统计年鉴[M].北京:中国统计出版社，2014.

[14]Li N，Liu X，Xie W，et al.The Return Period Analysis of Natural Di⁃sasters With Statistical Modeling of Bivariate Joint Probability Distri⁃bution[J].Risk Analysis，2013，33(1).

（责任编辑/易永生）

F406.2

A

1002-6487（2016）21-0049-06

国家自然科学基金资助项目(71172194；71221001；71390330；71390331)

舒 彤（1970—），男，江西波阳人，副教授，博士生导师，研究方向：供应链管理、商务智能。