一种应用于超大数据库的人脸识别方法

刘一平，袁富宇

（江苏自动化研究所，江苏连云港 222061）

一种应用于超大数据库的人脸识别方法

刘一平，袁富宇

（江苏自动化研究所，江苏连云港 222061）

针对数据库中待识别人脸数目巨大，计算困难的问题，提出了一种基于小波变换和主成分分析的人脸识别方法。该方法首先对数据库中的人脸进行小波变换，然后对小波变换后的图像进行主成分分析提取特征，将特征送入BP神经网络进行训练、识别。经过对比实验，结果表明：该方法可以在保证较高识别率的前提下，大大降低数据维数，从而该方法可以应用于超大数据库的人脸识别。

人脸识别；超大数据库；小波分解；主成分分析；BP神经网络分类器

人脸识别［1］是利用计算机技术从包含人脸的静止图像或视频序列中提取人脸个性化特征，并以此识别出人的身份的一种技术。如何有效地从人脸图像中提取特征并设计分类算法对特征进行分类识别是人脸识别的关键问题。在基于主成分分析的人脸识别系统［2］中进行实验发现，主成分分析法具有处理速度快、识别率高的特点，可以很好地用于实践。为减少主成分分析的计算量，可以用样本散布矩阵间接求得特征值及特征脸［3］。文献［4］在主成分提取特征之前先对图像进行小波分解，将分解后的子图像进行加权求和构成新的图像，然后对该图像进行主成分分析，实验证明该方法减少图像噪声对识别率的影响。文献［5］提出构建小波变换和稀疏表示的人脸识别分层框架也取得了不错的结果。

提取人脸个性化特征首先要解决人脸数据表示的问题，即如何将一个二维图像矩阵表示为一个低维个性特征向量。小波分解就是将一幅二维图像分解为不同频率的子图像，其中：高频成分代表图像边缘和细节，低频成分表示图像的主要内容，这样就降低了图像的尺寸。主成分分析是将高维信息在低维空间中进行投影，以投影系数作为特征向量，从而降低数据维数。通过对小波分解和主成分分析的融合，可以减少特征提取计算量，从而可以应用到超大数据库中。本文在小波分析（Wavelet Analysis，WA）和主成分分析的基础上设计新的特征提取方案，旨在适用于超大数据库的人脸特征提取，用反向传播（Back Propagation，BP）网络进行分类识别。实验证明，在保证正确识别率的情况下，该方法可以加快识别速度。

1 特征提取方法

1.1 小波分解

文献［6］提出了一种基于小波分析的人脸特征提取方法，利用小波变换的多分辨性，对人脸进行低维表达，然后在小波系数矩阵中直接进行特征定位和提取。图1是对图像用小波db3进行一阶分解的结果，从图片上可以看出：低频成分（LL）显示了人脸的主要成分；高频成分代表了细节和边缘轮廓（HH）。文献［6］还描述了小波变换的递推公式，通过连续对低频图像进行小波变换可以对一幅图像进行连续阶数的小波分解。

本文对小波分解后的低频图像和高频图像分别进行特征提取，将低频和高频特征进行组合构造新特征，以此来降低计算量。将一幅人脸图像用小波db3进行一阶小波分解，得到图像如图1所示。

1.2 主成分分析

1）基本原理

由正交变换，将存在冗余信息的P个原始向量变为M个彼此相互正交的新向量，而这M个相互正交向量中的前K个具有较大功率的向量成为主要成分，即主成分［7］。将这K个相互正交并且具有较大功率的向量张成一个子空间，将原始向量在该空间中进行投影，投影系数构成特征向量。

图1 一阶小波分解图像

主成分分析的本质就是将高维数据投影到低维空间中，从而实现数据降维，进而实现人脸特征提取［8］。

2）具体步骤

①图像数据库预处理

假设数据库中图像大小为R×W，训练样本数为N。将图像表示为n×1维向量，其中n＝R×W记为xi（i表示第i幅训练图像，i＝1，2，…，N）。生成训练样本集，记为：

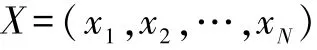
那么训练样本集的总体散布矩阵记为：

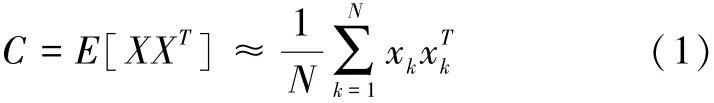
或者

②构造类间散布矩阵

假设第i（i＝0，1，2，…，p-1）个人有k幅图像，那么第i个人的平均图像就是

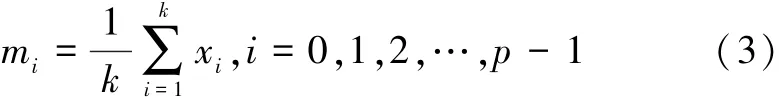
所有训练样本图像矢量的平均矢量为

其中：p是训练样本库中的总人数。

定义类间散布矩阵

其中p（wi）表示第i个人的人脸图像先验概率，p（wi）＝k／N。

③用S矩阵求特征向量

求散布矩阵S的特征值λ1，λ2，…，λn，并求得这些特征值所对应的正交特征向量u1，u2，…，un，并且有如下关系：λ1≥λ2≥…≥λn。取前t个较大的特征向量张成特征空间U，即U＝span｛u1，u2，…，ut｝。将图像x在特征空间U中进行投影，得

那么向量［k1，k2，…，kt］T就是图像X生成的特征向量。

图2是利用该方法进行人脸特征提取的效果展示，取占总能量90%的前t个最大特征值所对应的特征向量构成空间U＝span｛u1，u2，…，ut｝。将图像在该空间中投影，实验结果如图。那么α＝［8630.8，8739.9，-1752.9，2061.4，…］T就是左侧人脸图像的特征向量。

图2 主成分分析提取特征

1.3 BP神经网络

BP神经网络是一种基于误差反向传播的前馈神经网络，Robert Hecht⁃Nielson［9］已经证明具有单个隐含层的BP神经网络可以有效地逼近任意的连续函数。但是BP神经网络有容易陷入局部极小值的缺陷，可以用遗传算法对BP神经网络进行优化［10］。三层BP神经网络结构如图3所示。

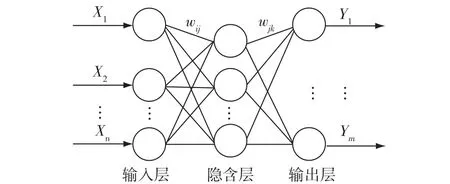
图3 三层BP神经网络

BP神经网络是将原始输入信号正向传播，经隐含层到达输出层。如果输出的结果不满足期望，就会在输出层产生误差信号，则将误差信号作为调整信号反向传播。在本文中，输入层的输入就是第1.2节中产生的人脸特征向量；输出层的期望输出就是每个人的编号，一般情况下用0、1表示，即输出40维列向量，第i个人的期望输出为第i个元素为1其余元素为0的40维向量。本文中的期望输出用0.1、0.9表示，因为不同样本之间存在一定得模糊性，实验也证明该方法识别率有所提高。

2 基于超大数据库的人脸识别方法

2.1 改进特征提取方法

本文介绍了主成分分析方法，其中假设数据库中图像大小为R×W，训练样本数为N。将图像表示为n ×1维向量，其中n＝R×W，记为xi（i表示第i幅训练图像，i＝1，2，…，N）。生成训练样本集，记为：

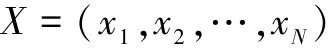
那么训练样本集的总体散布矩阵记为：

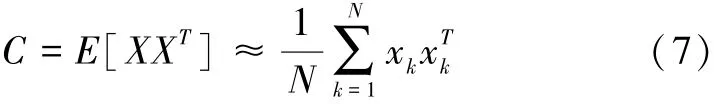
或者

ORL数据库中图像大小为112×92，即R＝112，W＝92；样本数为200，即N＝200。

那么矩阵X的大小为10304×200，总体散布矩阵C为10304×10304的矩阵。如此大的矩阵要计算出其特征值、特征向量是很困难的，为了克服这个困难，我们可以根据奇异值定理求XTX200×200的特征值和特征向量来间接求得C的特征值、特征向量。算法如下：

假设XTX的r个特征值为λ1，λ2，…，λr相应的特征向量为v1，v2，…，vr。由奇异值（SVD）分解定理［7］，XTX相应的特征向量为

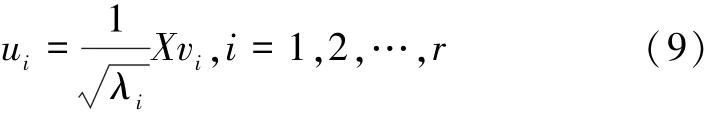
那么特征脸空间为U＝span｛u1，u2，…，ur｝。

根据奇异值分解定理可以将求C10304×10304的特征值变为求一个200×200矩阵的特征值，大大减少了计算量。但是随着数据库的增大，当样本容量N≫200，即使使用奇异值定理，新的矩阵为N×N，该矩阵也很难计算特征值和特征向量。

本文就是计算当数据容量N≫200时，通过降低散布矩阵维数进而减少计算量，使得主成分分析方法不因为数据容量增加而变得不可实现。

本文思路是：在生成训练样本之前，首先对每幅人脸图像进行小波变换，旨在降低图像尺寸；用小波变换后的尺度较小的低频和高频图像构造训练样本矩阵，然后分别对低频和高频图像分别进行特征提取；最后将低频和高频特征进行融合送入BP神经网络进行分类识别。例如ORL数据库图像为10304维，如果进行小波变换使得图像降低为K维记为x′，K≪10304，那么不用利用奇异值定理，训练样本的总体散布矩阵就变成：

C的尺寸将会变成K×K，计算复杂度降低，使得处理超大数据库更加简单。

2.2 计算步骤

1）小波变换

本次实验使用ORL数据库，数据库中共40个人，每人10幅图像。取每人前5幅图像，共200幅图像，作为训练样本集，剩余图像作为测试样本集。图4为ORL中两个人的人脸数据库。

图4 ORL部分人脸数据库

首先将人脸图像进行小波变换，分别取低频、高频图像A、B，按照上文步骤生成训练样本集：

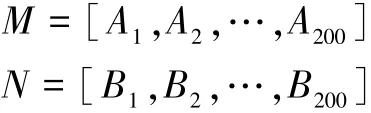
如果进行三阶小波变换，那么M、N均是270×的矩阵。

2）主成分分析

步骤1）得到了低频人脸数据库M和高频人脸数据库N。按照如下公式分别求得M和N的散布矩阵。

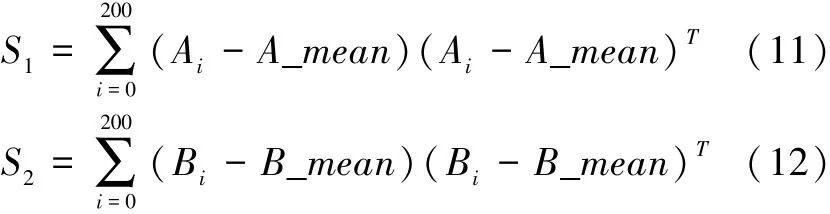
其中，A-mean和B-mean分别为低频人脸库和高频人脸库的平均脸向量。

分别求得矩阵S1和S2的特征值和特征向量，取占能量90%的前k个特征值的个数作为子空间维数，生成两个特征子空间U＝span｛u1，u2，…，uk｝和V＝span｛v1，v2，…，vl｝。

将每幅人脸图像的低、高频图像分别在低频子空间和高频子空间中进行投影，得到两个特征向量。即任意幅图像i对应两个特征向量：

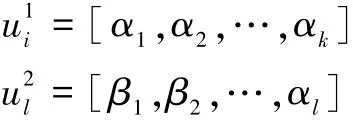
3）BP神经网络分类识别

将得到的每幅图像的两个特征向量，分别送入BP神经网络进行分类识别；或将两个特征向量进行融合，构成一个特征向量，送入BP神经网络进行分类识别。训练样本送入神经网络训练之前，要将训练样本输入顺序随机打乱，这样便于充分训练，提高识别率。

3 仿真实验

本文实验分为四部分：1）原来方法的复现，直接对图像进行主成分特征提取；2）首先将图像进行一阶小波分解，对低频和高频图像分别进行主成分分析提取特征，对特征进行分类识别；3）将2）生成的低频图像再次进行小波分解，将分解后的低频和高频图像分别进行主成分分析提取特征，对特征进行分类识别；最后是把3）生成的低频图像再次进行小波变换，然后对低频和高频图像分别进行主成分分析提取特征，对特征进行分类识别。

3.1 原始图像的主成分特征识别

将原始训练图像按列展成向量，例如将第i幅图像展成列向量xi（i＝1，2，…，200），构成矩阵X＝（x1，x2，…，x200）。根据奇异值定理求X的特征值、特征向量，将特征值按照从大到小顺序排列。占总能量90%的特征值个数是71，即取前71个最大特征值对应的特征向量构成主成分子空间，将图像在该子空间上进行投影得到特征向量，特征向量维数是71。

表1 隐含层神经元个数对识别率影响

将特征送入BP神经网络进行确认识别，实验中隐含层取值范围为多次实验获得的峰值附近；改变隐含层神经元的数目进行10次实验，表中为10次实验中的最大值和最小值及平均值，结果如表1、图5。可以看出，不进行小波变换，即不损失原始信息的前提下，识别率可以达到90%左右；识别率在一定范围内随隐含层神经元个数增加而增加，但是二者不成正比例关系。

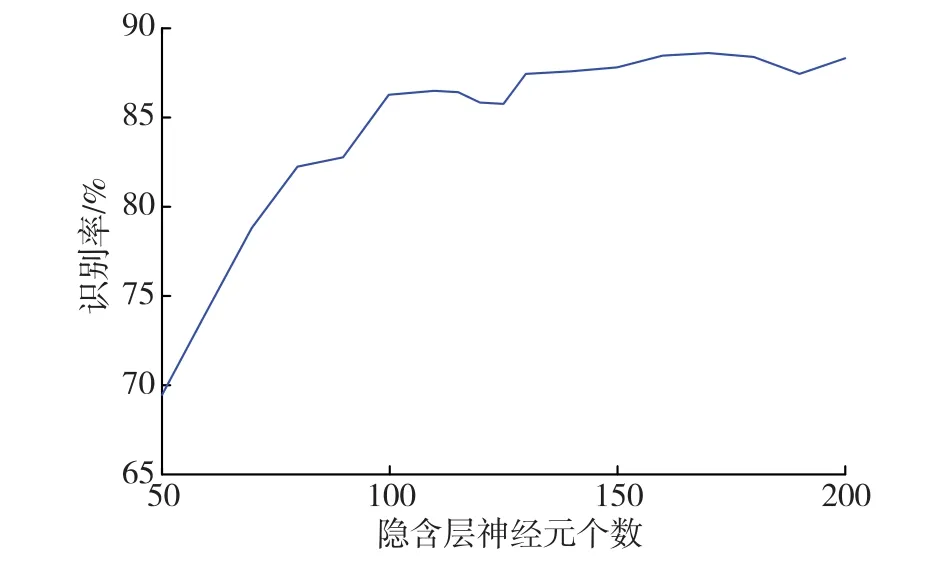
图5 识别率与隐含层节点数关系折线图

3.2 一阶小波图像的主成分特征识别

对原始图像进行小波变换，得到一阶小波变换的低频图像矩阵和高频图像矩阵S1、S2。分别计算S1、S2的特征值，占总能量90%的特征值个数分别是59、141。可知看出，高频矩阵的特征值比较均匀，即能量没有集中在少数几个特征向量上。用低频特征进行仿真实验，然后在将低频和高频特征进行融合计算识别率。

1）低频特征仿真实验

用低频散布矩阵的前59个特征值（其和大于所有特征值和的90%）对应的特征向量作为子空间，将图像在该子空间中进行投影，提取特征向量。经实验，该向量为59维，构造输入层神经元为59，输出层神经元个数为40，隐含层神经元个数可变的BP神经网络进行仿真实验。实验结果如表2，低频特征识别率与隐含层神经元个数关系如图6。

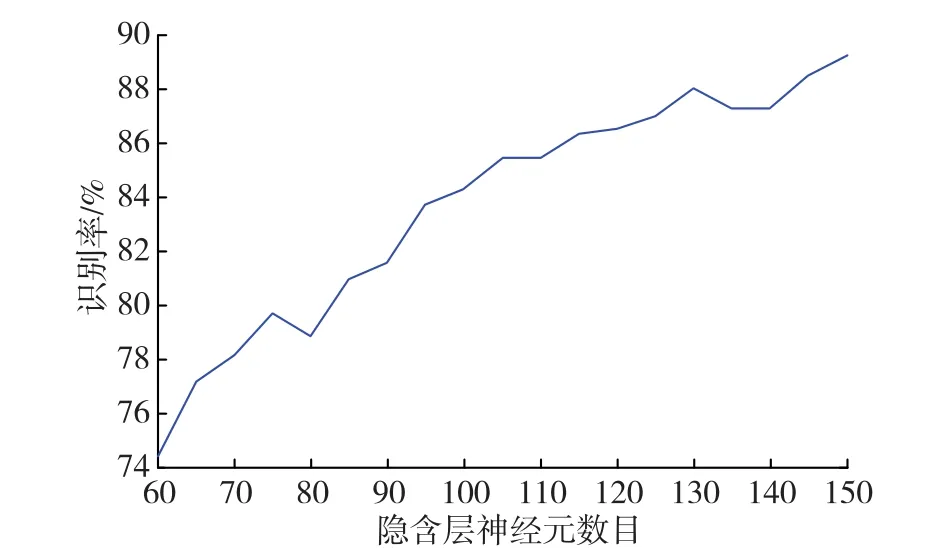
图6 识别率与隐含层神经元个数关系

从表2、图6可以看出一阶小波变换后，低频图像的主成分特征的识别率可以达到90%左右，即人脸图像主要信息包含在低频成分中；识别率和隐含层神经元数目不成比例关系。

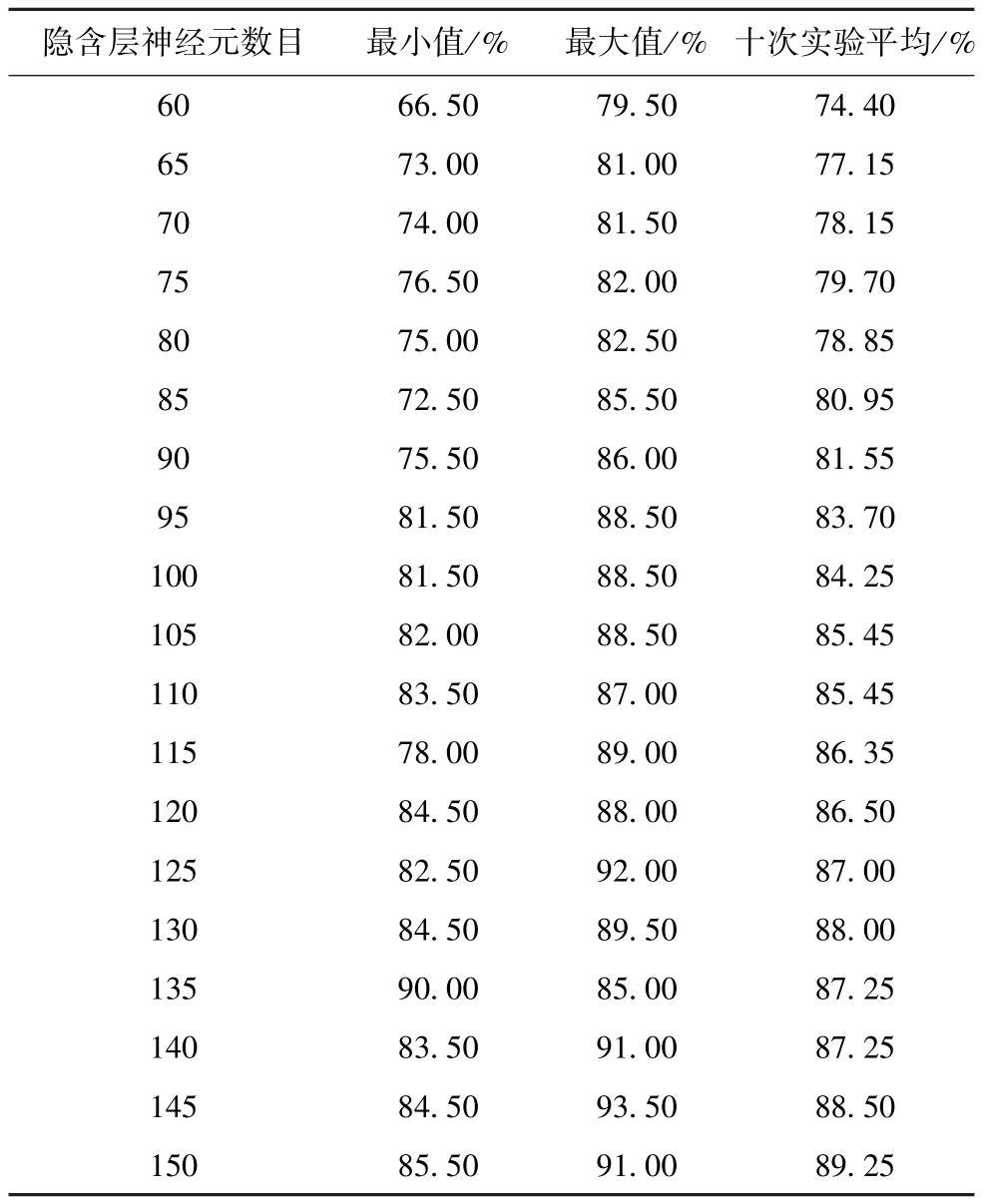
表2 识别率与隐层神经元个数关系

2）低频、高频融合特征仿真实验

将图像低频特征和部分高频特征融合成一个新的向量，用该特征作为图像的特征向量进行识别，结果如表3所示。

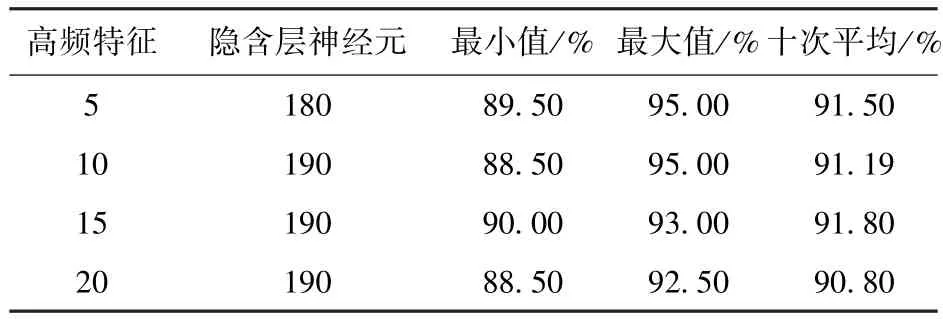
表3 高频特征个数与识别率关系

小波分解后，图像维数由原来的10304降低到2784，变为原来的27.02%。计算量大大降低，而实验结果却几乎不受影响，且识别结果很稳定。

本次实验发现只用图像低频和高频成分进行分类识别可以保证较高的识别率，但是计算量大大减少，而且不受数据库人脸数增多的影响，因此该方法可以应用到超大人脸数据库的人脸识别中；随着隐含层神经元数量的增加，识别率有所提高，但是神经元增多网络结构更加复杂，甚至出现过拟合现象。

为了验证低频成分在多大程度上保持原始图像信息，下面对原始图像分别计算二阶和三阶小波变换，然后提取特征、计算识别率。

3.3 二阶小波图像的主成分特征识别

对一阶小波变换得到的低频图像S1再次进行小波变换，得到二阶小波变换的低频图像矩阵和高频图像矩阵S11、S12。分别计算S11、S12的特征值及特征向量，占总能量90%的特征值个数分别是42、122。用低频特征进行仿真实验，然后在将低频和高频特征进行融合计算识别率。

1）低频特征仿真实验

用低频散布矩阵的前42个特征值（其和大于所有特征值和的90%）对应的特征向量作为子空间，将图像在该子空间中进行投影，提取特征向量。经实验，特征向量为42维，构造输入层神经元为42、输出层神经元个数为40、隐含层神经元个数可变的BP神经网络进行三次实验。实验结果如表4。

表4 识别率与隐含层神经元关系

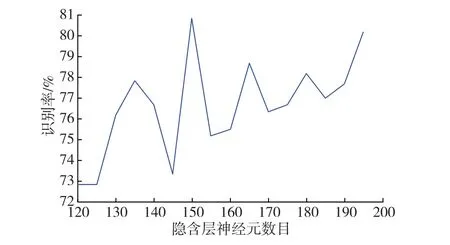
图7 识别率与隐含层神经元个数关系

低频特征识别率与隐含层神经元个数关系如图7。对比实验二，图像大小变为原来的7.82%，计算量大大降低；图像识别率有所下降，但是仍保持较高水平，即二阶低频图像仍保持原始图像的主要信息。

2）低频、高频融合特征仿真实验

将图像低频特征和部分高频特征融合成一个新的向量，用该特征作为图像的特征向量进行识别，实验结果如表5所示。

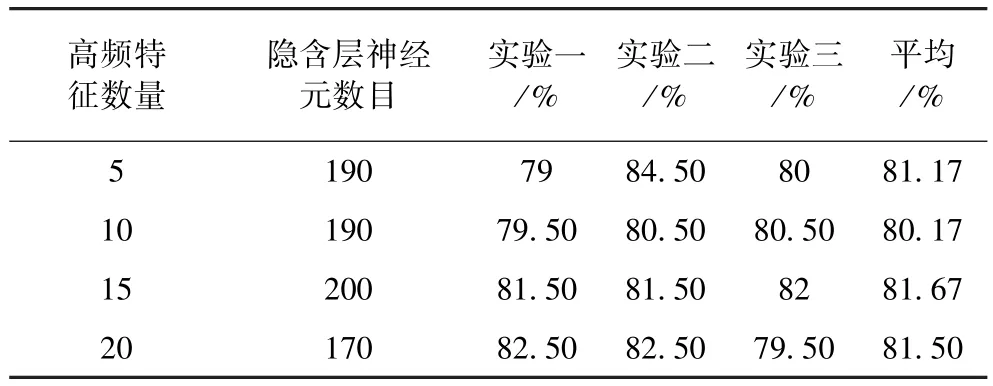
表5 高频特征个数与识别率关系

二阶小波分解后，图像维数降低为806，变为原来的7.82%。计算量大大降低，而实验结果仍然保持较高水平；融合了低频和高频特征的特征向量，识别率有所提高。

3.4 三阶小波图像的主成分特征识别

对二阶小波变换得到的低频图像S11继续进行小波变换，得到三阶小波变换的低频图像矩阵和高频图像矩阵S111、S112。通过实验，分别求得S111、S112的特征值，占总能量90%的特征值个数分别是25、77，然后将低频、高频特征分别进行仿真实验，最后将二者组合在一起进行仿真实验。

1）低频特征仿真实验

用低频散布矩阵的前25个特征值（某和大于所有特征值和的90%）对应的特征向量作为子空间，将图像在该子空间中进行投影，提取特征向量。经实验，该向量为25维，构造输入层神经元为25、输出层神经元个数为40、隐含层神经元个数可变的BP神经网络进行仿真实验。实验结果如表6。

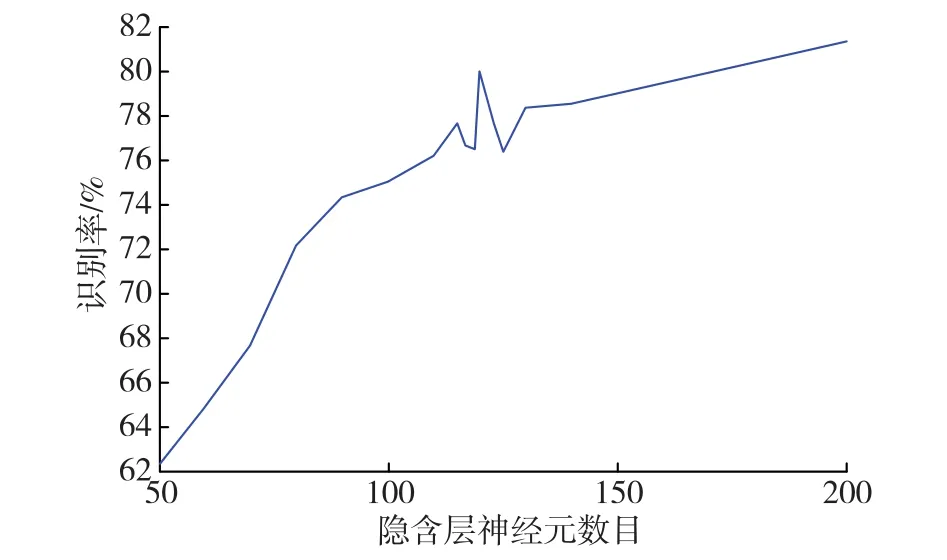
图8 低频图像识别率与隐层神经元个数关系

低频图像识别率与隐含层神经元个数n的关系折线图如图8所示。从表6、图8中可以看出，在一定范围内识别率随着隐含层神经元个数增加而有所提高，但是在达到某一识别率后上升缓慢，甚至有所回落；低频图像像素数点为270，即经小波变换原始图像尺寸变为原来的2.62%，但依然保持较高的识别率。

表6 低频图像识别率与隐层神经元个数关系

2）高频特征仿真实验

用高频散布矩阵的前77个特征值（其和大于所有特征值和的90%）对应的特征向量作为高频子空间，将图像在该子空间中进行投影，提取特征向量。经实验，该向量为77维，构造输入层神经元为77、输出层神经元个数为40、隐含层神经元个数可变的BP神经网络进行仿真实验。实验结果如表7。

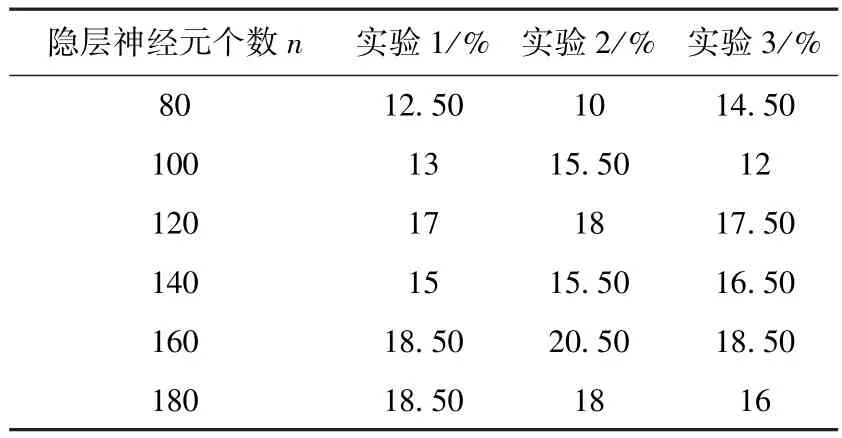
表7 高频图像识别率与隐层个数关系

从图7可以看出，用高频图像提取的特征进行仿真实验会失效。

3）低频、高频融合特征仿真实验

前面两个实验中说明低频成分可以用来识别人脸，高频成分可以用来定位人脸。本次实验是在原来低维特征向量（25维）的基础上融合了高频特征（n个，共25+n维特征向量），来检验二者融合后识别率变化。实验结果如表8。

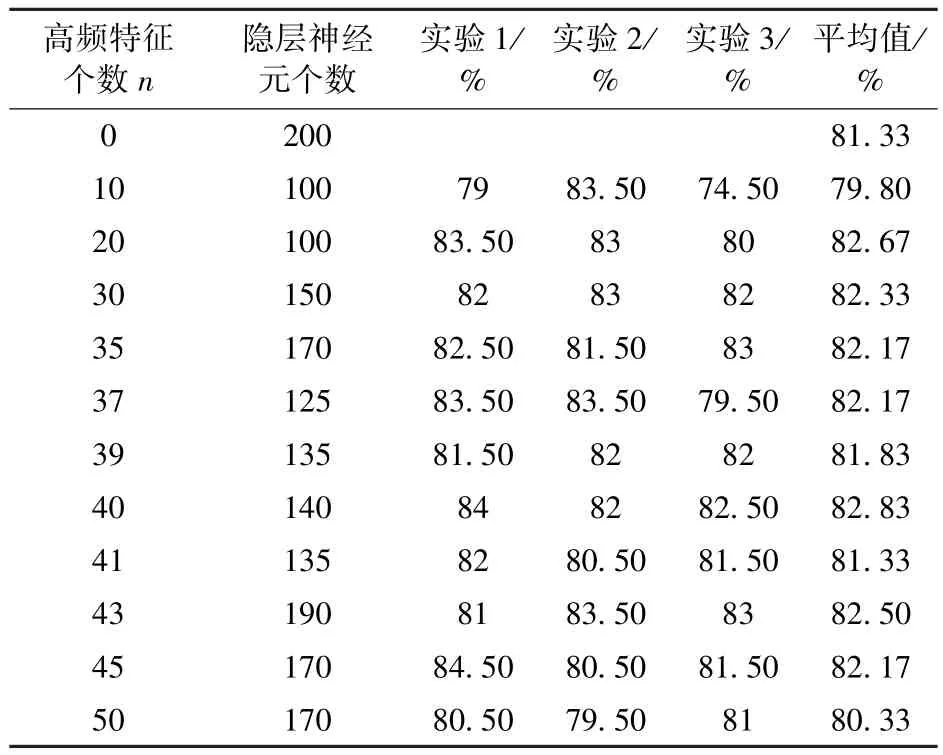
表8 高频特征个数与识别率关系

图9 高频特征个数与识别率关系折线图

表8中隐含层神经元个数是在确定了输入层神经元个数（25+n）的个数以后，经过反复实验测得的最佳结果。图9为识别率与高频神经元个数关系折线图。

3.5 实验结果分析

综上4个实验可以看出，用以区别人脸的主要特征集中在低频成分中；高频成分包含人脸轮廓和细节，主要是人脸的共性成分。所以在很多情况下可以用高频图像定位人脸，用低频图像来识别人脸。下面考虑用融合了低频成分和部分高频成分的特征向量来识别人脸。

通过对改进实验结果和原始实验结果对比后发现，该方法可以大大减少训练矩阵尺度；一阶小波分解后产生的特征向量可以保持和原始图像相当的识别率，即使是三阶小波分解产生的特征也在减少计算量大同时保持了较高的识别率。

该方法旨在研究超大数据库的识别方法，所以在识别率上并没有很好的提高。仅有在一阶小波分解时识别率略有提高，其他阶的小波分解识别率甚至有所下降。

实验中还发现：

1）融合了低频图像特征向量和高频图像的特征向量，识别率有显著提高；

2）和直接将图像进行PCA特征提取的特征向量相比，上述方法除了在计算量上大大减少之外识别率差别不大。即融合低频和高频图像特征向量的新特征向量可以在不牺牲识别率的条件下大大降低计算量；

3）随着特征向量维数的不断增加，在保证最优识别率的条件下，隐含层神经元个数也在不断增加，即BP伸进网络中输入层神经元个数增加，隐含层神经元个数也需随之增加。

4 结束语

本文是在小波图像变换和主成分分析的基础上，提取图像特征向量，用BP神经网络进行分类识别。实验表明一阶小波变换后，像素数变为原来的27.02%，计算量大大降低，但是识别率几乎不变，即小波变换后图像很好地保持了图像可以用来识别的个性，这也是该方法的可行条件。通过三阶小波变换，可以将用来定位人脸的高频成分和用于识别人脸的低频成分提取出来。经过三阶小波分解提取出来的低频和高频图像的像素数仅为原始图像像素数的2.62%，计算量大大减少。经过仿真实验，这种方法不会太大降低识别率，可以用来处理超大人数据库人脸识别问题。

［1］ 肖兵，王映辉.人脸识别研究综述［J］.计算机应用研究，2005，22（8）：1⁃5.

［2］ 谭光鸿，王兵.基于主成分分析法的人脸识别系统构建［J］.装备制造技术，2016（5）：219⁃220.

［3］ 郭黎，冷洁，梅文兰，等.基于PCA和SVM的人脸识别技术研究［J］.湖北民族学院学报（自然科学版），2015，33（2）：193⁃196.

［4］ 龚飞，金炜，付冉笛，等.融合小波包细节子图及稀疏表示的人脸识别［J］.光电工程，2016，43（6）：36⁃42，54.

［5］ 翟素兰，曹庆，谢文浩.基于稀疏表示与小波特征的人脸识别分层框架［J］.计算机工程与应用，2016，52（14）：146⁃149，171.

［6］ 付瑶，刘志镜，谷明波.基于小波分析的人脸特征提取方法［J］.计算机工程与科学，2002，24（6）：52⁃54.

［7］ 张贤达.矩阵分析与应用［M］.第2版.北京：清华大学出版社，2013.

［8］ 李康顺，李凯，张文生.一种基于改进的BP神经网络的PCA人脸识别算法［J］.计算机应用与软件，2014，31（1）：158⁃161.

［9］ Robert Hecht⁃Nielson.Theory of the Back Propagation Neural Network［J］.Proceedings of the Internal Joint Con⁃ference on Neural Networks，1989：593⁃605.

［10］崔向东，崔婧楠.基于GA⁃BP神经网络的人脸识别方法研究［J］.安徽职业技术学院学报，2016，15（2）：30⁃32.

A Face Recognition Method Applied to Huge Databases

LIU Yi⁃ping，YUAN Fu⁃yu
（Jiangsu Automation Research Institute，Lianyungang 222061，China）

Traditional face recognition methods can’t work well，if there are too many faces in the database.In order to solve the problem，this paper presents a face recognition method based on wavelet transform and principal component analy⁃sis.Experimental results show that the method can guarantee a high recognition rate，by greatly reducing the data dimension.

face recognition；huge database；wavelet analysis；PCA；BP neural network classifier

TP391

A

10.3969／j.issn.1673⁃3819.2016.06.025

1673⁃3819（2016）06⁃0118⁃07

2016⁃08⁃31

2016⁃10⁃13

刘一平（1990⁃），男，山东潍坊人，硕士研究生，研究方向为基于深度学习的人脸识别技术。

袁富宇（1964⁃），男，研究员，博士生导师。