基于激光测距和惯导的非合作目标远程交会相对导航算法研究

杨东春,赵春慧,顾冬晴

(1.上海航天技术研究院,上海 201109; 2.上海宇航系统工程研究所,上海 201109)



基于激光测距和惯导的非合作目标远程交会相对导航算法研究

杨东春1,赵春慧2,顾冬晴2

(1.上海航天技术研究院,上海 201109; 2.上海宇航系统工程研究所,上海 201109)

对非合作目标的远程交会，研究了一种基于激光测距和惯导的相对导航方法。给出了由激光测距仪和惯性传感器组成的相对导航系统。设计了相对导航算法：用激光测距获得的相对距离和相对方位、俯仰角度与惯导获得的姿态和位置信息，确定目标飞行器与追踪飞行器相对轨道动力学方程并进行递推，输出相对位置与速度；用激光测距输出的相对距离和相对方位、俯仰角度与惯导获得的姿态、位置信息，由卡尔曼滤波得到相对位置与速度的误差并对递推结果进行修正，修正的结果作为相对导航最终的输出。算例表明：该相对导航方法适于非合作目标远程交会，在远程交会结束时刻，相对位置误差小于1 m，相对速度误差小于0.05 m/s；相对导航滤波器的加速度计常值偏差估计误差明显小于绝对导航滤波器。

非合作目标； 远程交会； 相对导航； 激光测距； 惯导； 相对轨道动力学； 相对距离； 相对姿态； 卡尔曼滤波

0 引言

相对导航是空间飞行器交会对接中的关键技术，与非合作目标进行交会时因不能与目标进行通信而无法获取目标精确的导航定位信息，故非合作目标交会对接中的相对导航更具挑战性[1]。对自主相对导航已进行了大量研究：文献[2]解释了自主交会和对接的各方面，包括交会的不同阶段及所需的传感器，传感器的配置基于目标飞行器为被动、无动力和非合作的状态；文献[3]对远程导引脉冲变轨方案的有限推力修正进行了研究，可消除转换误差和摄动模型误差；文献[4]给出了差分GPS和激光雷达导航在自主交会的相对接近段(10 km～500 m)和最后逼近段(550～2 m)直至两飞行器完成交会对接中的应用，该法已在ETS-Ⅶ验卫星上已得到了验证；文献[5]改进了一种相对导航滤波器用于航天飞机与尾迹屏罩设备的交会对接，两个飞行器均配置了GPS接收机，交会时尾迹屏罩设备将GPS接收机输出的数据传给航天飞机；文献[6]阐释了两个飞行器处于百米以内距离时基于激光测距的相对导航卡尔曼滤波器的优势，由于距离较近对传感器指向精度的要求不高，且导航算法建立在当地水平当地垂直(LVLH)坐标系中的简洁线性相对动力学关系的基础上；文献[7]仿效空间综合全球定位系统/惯性导航系统(SIGI)卡尔曼滤波器解决了与国际空间站接近的问题，但未对相对导航或电子-视觉传感器及姿态指向进行研究；文献[8]提出了仅利用角度信息进行相对导航的方法，由于追踪飞行器与目标飞行器相对距离较近(25 m以内)，目标图像几乎充满了传感器的整个焦平面，对接时相对姿态估计显得尤其重要；文献[9]探讨了一种利用惯性导航系统配合扩展卡尔曼滤波实现相对导航的方法，进行相对位置、速度，相对姿态和姿态变化率的估计，适合中等距离的非合作目标交会问题。文献[10]介绍了基于光学的相对导航方式，光学测量方法的测姿精度较高，同时具有相对定位和定姿的功能。激光测距仪可测得相对距离、相对俯仰角和方位角，经过滤波得到相对位置、速度误差，对相对导航中的相对位置与速度进行修正，可获得相对导航所需的精度。基于激光测距仪和惯性器件测量，本文对非合作目标远程交会(与目标距离大于数公里)的相对导航算法进行了研究。

1 非合作目标远程交会相对导航系统

本文设计的非合作目标远程交会相对导航系统如图1所示。

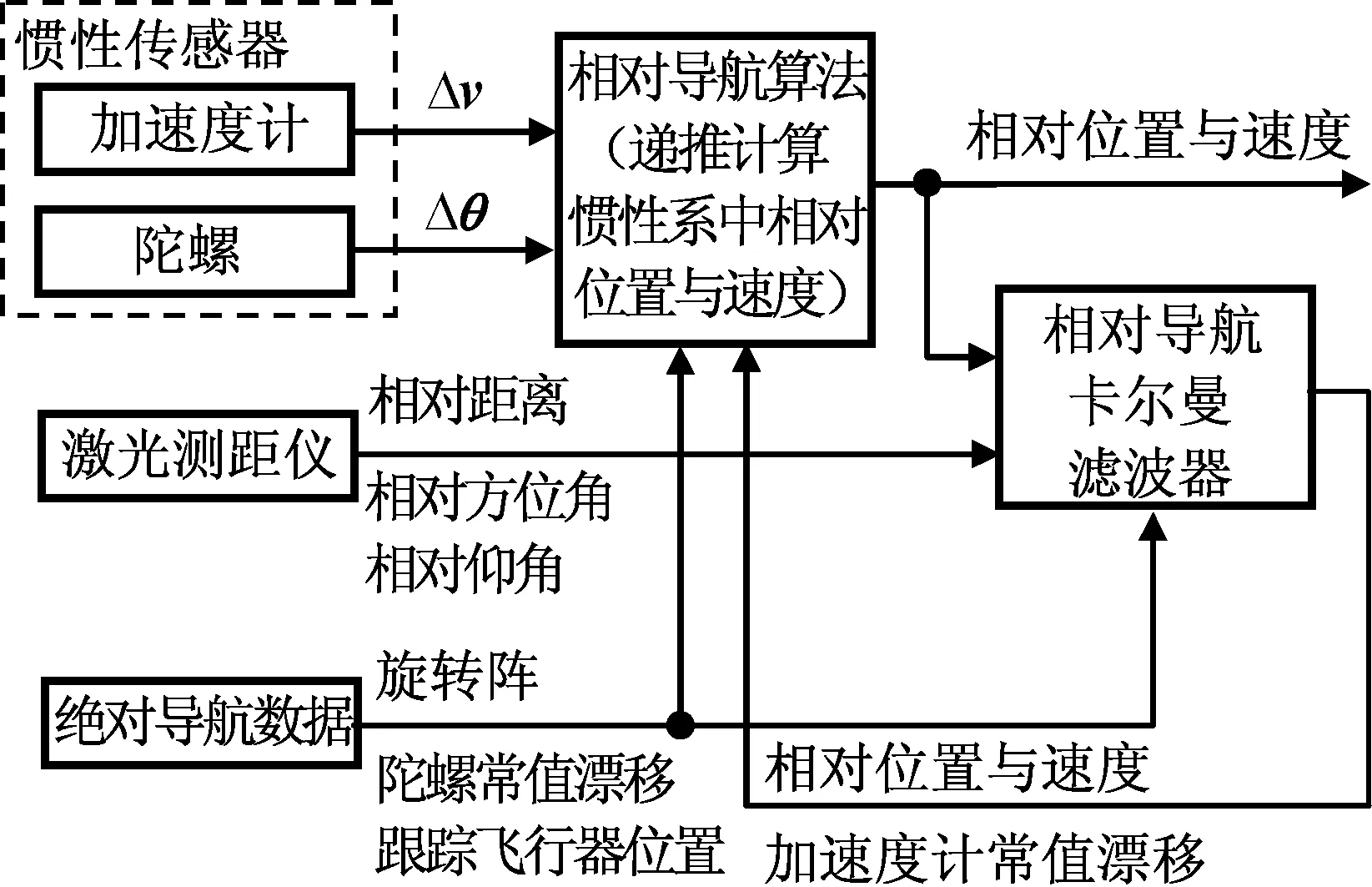
图1 非合作目标远程交会相对导航系统Fig.1 Non-coorperative target long-distance rendezvous relative navigation system

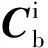
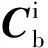
2 相对导航算法

对非合作目标远程相对导航，将i系中的相对位置与速度作为导航参数。一般合作目标的相对导航的导航参数为目标轨道系中的相对位置与速度，但计算目标轨道系中的相对位置与速度需获知较精确的目标飞行器在i系中的位置和速度。对非合作目标来说，虽然目标飞行器在i系中的位置和速度可预报，但如降低对目标飞行器在i系中的位置和速度预报精度的要求，可使非合作目标交会的实施更灵活。采用i系中的相对位置与速度作为相对导航参数，则无需对目标飞行器在i系中的位置和速度进行精确预报，仅确定目标飞行器在i系中的大致位置，使激光测距仪能捕获目标即可。因绝对导航系统可输出跟踪飞行器在惯性系中的位置和速度，若相对导航能输出i系中的相对位置与速度，则目标飞行器在i系中的位置和速度也能获得，故亦可得到目标轨道系中的相对位置与速度。

跟踪飞行器和目标飞行器的轨道动力学方程分别为

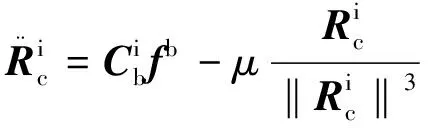
(1)

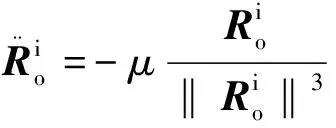
(2)

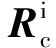
定义i系中的相对位置为i系中跟踪飞行器和目标飞行器位置的差，即

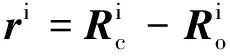
(3)

将式(3)代入式(2)并与(1)相减，可得

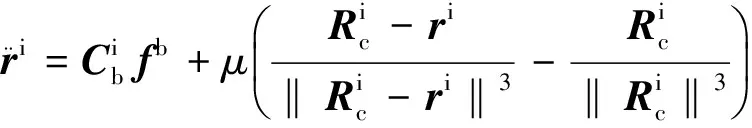
(4)

式(4)即为i系中的相对动力学方程。

在时间区间[tk-1,tk]中，用捷联惯导速度更新的数值积分方法对式(4)进行积分，可得

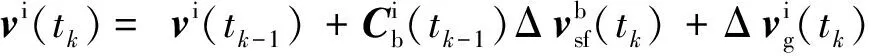
(5)

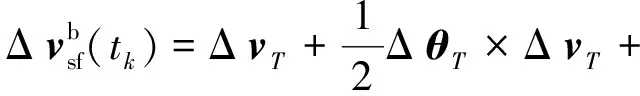
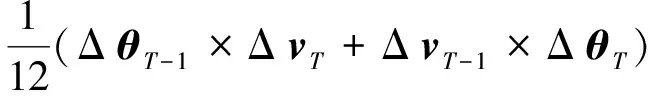
(6)

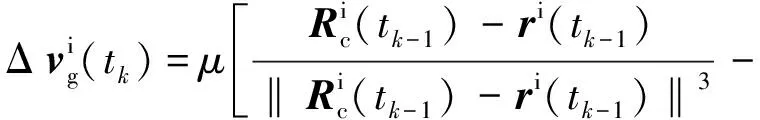
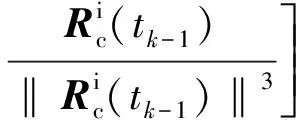
(7)

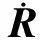
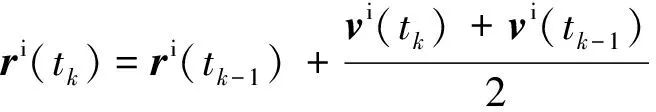
(8)

式(5)～(8)即为i系中相对位置和速度递推计算的算式。

3 相对导航卡尔曼滤波器

定义i系中相对位置和速度的误差为

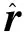
(9)

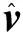
(10)

基于式(4)、(9)、(10)，可得相对位置与速度误差方程为

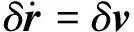
(11)

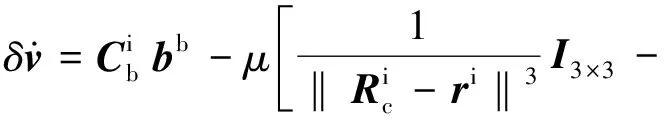
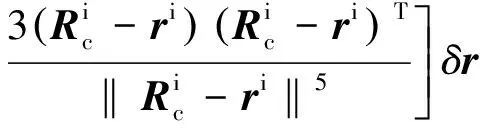
(12)

式中：bb为加速度计常值偏差，且

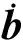
(13)

相对导航的卡尔曼滤波器估计相对位置与速度误差，以及加速度计常值偏差。用反馈校正，修正计算得到的相对位置与速度，以及加速度输出的速度增量。相对导航卡尔曼滤波器的状态向量

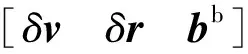
(14)

卡尔曼滤波的系统状态方程为

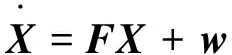
(15)

式中：w为系统状态噪声；F为系统状态阵，其具体形式可由式(11)～(13)确定。

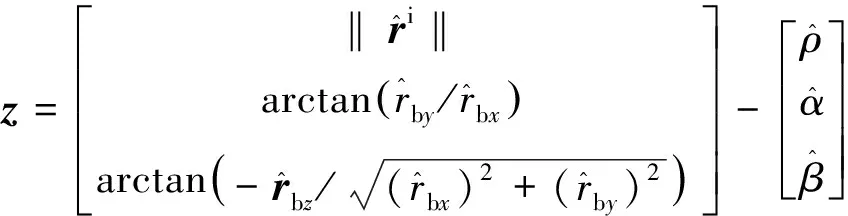
(16)

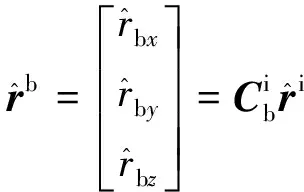
(17)

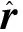
z=HX+v；

(18)

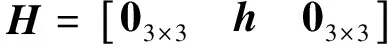
(19)

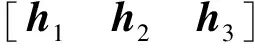
(20)

式中：v为由激光测距仪量测噪声确定的系统量测噪声；H为量测矩阵；

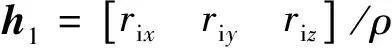
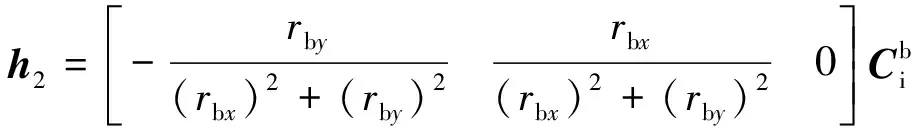
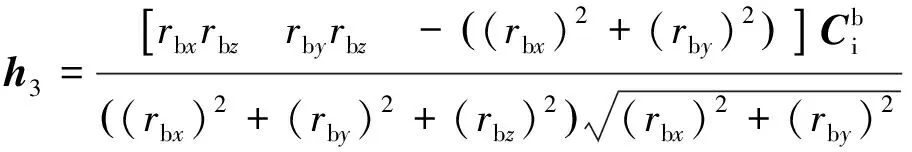
此处：rix，riy，riz为ri的三轴分量；ρ为相对距离。

获得系统方程和观测量后，用卡尔曼滤波基本方程可得系统状态的最优估计。

4 仿真

由于非合作目标远程交会相对导航中需使用来自绝对导航系统的数据，仿真中加入绝对导航系统，绝对导航系统为惯性/GPS/天文组合导航系统。仿真中：

a)产生激光测距仪量测时，数据更新周期1 s。考虑目标视线方向的方位角和仰角测量误差为均值0、标准差0.02°的白噪声；相对距离测量误差为均值0的白噪声，其标准差由两项之和构成，一项为固定值5 m，另一项为相对距离的0.000 6倍。

b)产生加速度计量测时，数据更新周期0.02 s。考虑加速度计量测误差由常值偏差、一阶高斯马尔可夫慢变漂移(系统建模时未加入模型，该慢变漂移在仿真中视为不可建模误差)，以及白噪声(速度随机游走)构成。其中常值偏置误差1×10-3m/s2；一阶高斯马尔可夫过程相关时间1 200 s、均方根1×10-4m/s2；白噪声均值0、(随机游走系数)标准差5×10-4m/s0.5。

c)产生陀螺量测时，数据更新周期0.02 s。考虑陀螺量测误差由常值偏差、一阶高斯马尔可夫慢变漂移(系统建模时未加入模型，该慢变漂移在仿真中视为不可建模误差)，以及白噪声(角随机游走)构成。其中常值偏差3.5 (°)/h；一阶高斯马尔可夫过程相关时间600 s、均方根0.15 (°)/h；白噪声均值0(随机游走系数)、标准差0.025 (°)/h0.5。

d)产生星敏感器量测时，数据更新周期1 s。考虑星敏感器量测误差为均值0、标准差7.5″的白噪声。

e)产生红外地球敏感器量测时，数据更新周期1.5 s。考虑红外地球敏感器量测误差由常值偏差、一阶高斯马尔可夫慢变漂移(系统建模时未加入模型，该慢变漂移在仿真中视为不可建模误差)，以及白噪声构成，其中常值偏差为0.05°，一阶高斯马尔可夫过程相关时间3 600 s、均方根0.005°；白噪声均值0、标准差0.02°。

f)仿真产生GPS伪距时，数据更新周期1 s。考虑伪距量测为均值0、标准差30 m的白噪声；GPS接收机初始钟差等效距离误差10 km，钟漂等效速度误差0.1 m/s，且仿真中设钟漂等效速度误差为均值0、标准差0.001 m/s的白噪声。

设仿真时间3 h，仿真产生真实运动轨迹时考虑地球非球形摄动的J2，J3，J4项，并加入相关时间3 600 s，均方根1×10-7m/s2的一阶高斯马尔可夫过程作为扰动加速度项。采用LQR闭环反馈控制实现远程交会，远程交会过程为从距目标50 km处机动至距目标2 km处，远程交会的单向推力由2台25 N发动机(共计50 N)提供。令跟踪飞行器总质量为1.5 t。仿真中，在目标飞行器轨道系中跟踪飞行器相对目标飞行器的相对位置如图2所示，相对距离如图3所示。

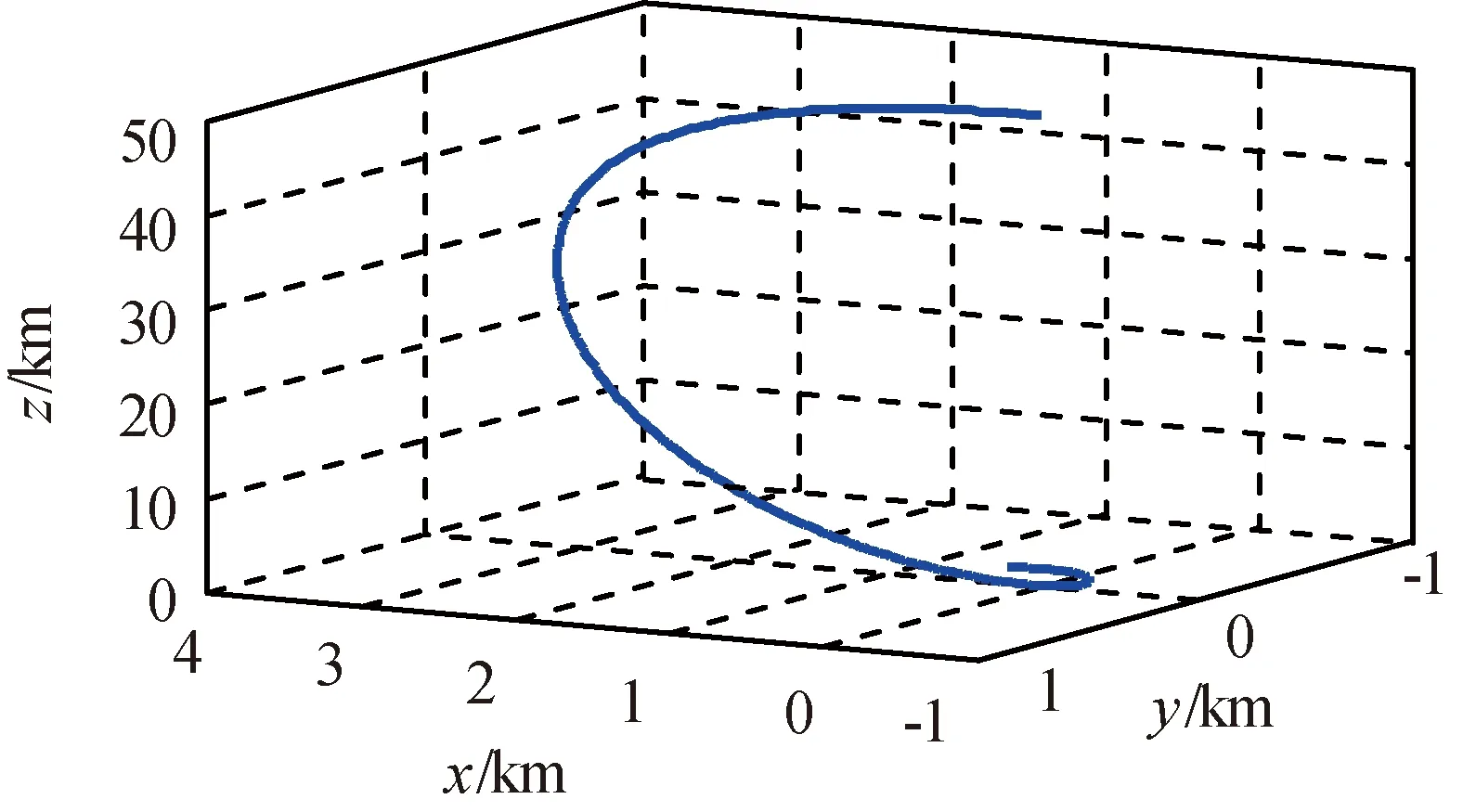
图2 目标飞行器轨道系中相对位置Fig.2 Relative position in target orbit coordinate

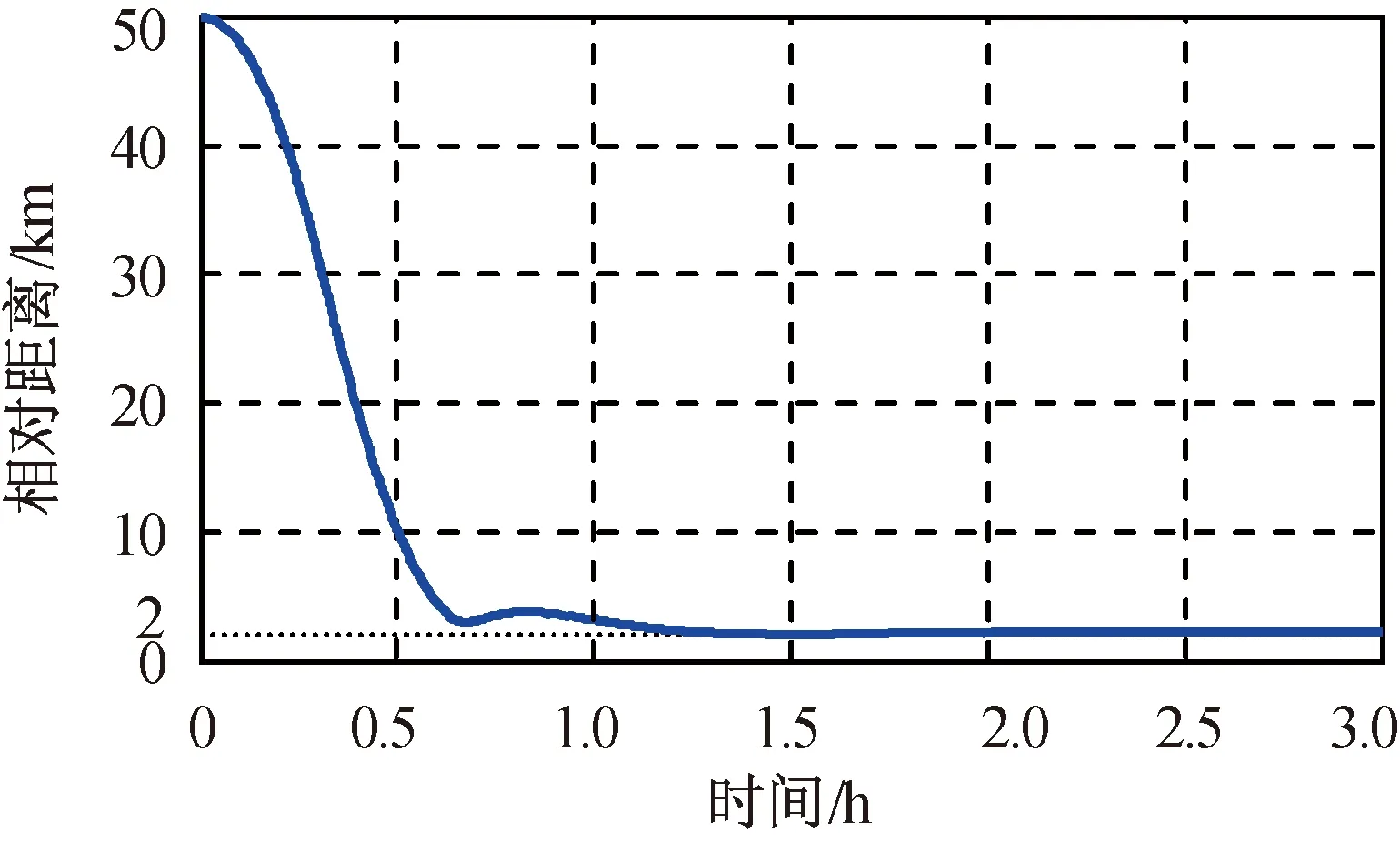
图3 相对距离Fig.3 Relative distance

仿真中假设GPS接收机不仅可接收GPS卫星发射的主瓣信号，而且能接收发射半角28°～35°的旁瓣信号， GPS卫星可见性如图4所示。

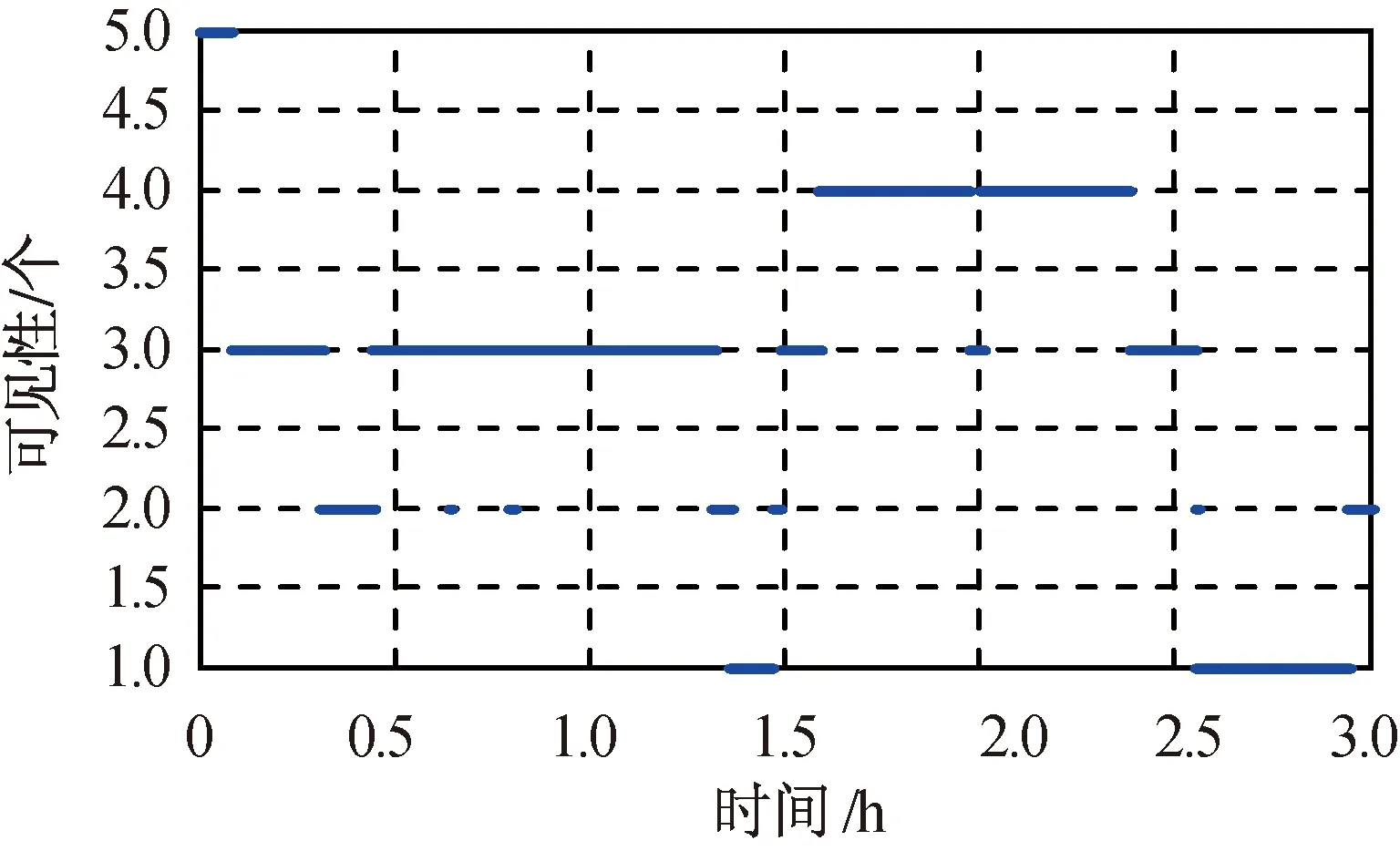
图4 GPS卫星可见性Fig.4 Visible GPS

因远程交会的轨道控制中，常需使用目标飞行器轨道系中的相对位置和相对速度(如LQR闭环反馈控制)，故将i系中的相对位置和相对速度转为目标飞行器轨道系中的相对位置和相对速度。仿真所得目标飞行器轨道系中的相对位置和相对速度误差分别如图5、6所示，相对导航滤波器的加速度计常值偏差估计误差如图7所示，绝对导航滤波器的加速度计常值偏差估计误差如图8所示。由图5～8可知：相对导航滤波在0.5 h后收敛，且滤波收敛后相对导航滤波器的加速度计常值偏差估计误差精度明显优于绝对导航滤波器的加速度计常值偏差估计误差。在仿真结束(即远程交会结束)时刻，目标飞行器轨道系中的相对位置误差和相对速度误差，以及加速度计常值偏差估计误差见表1。

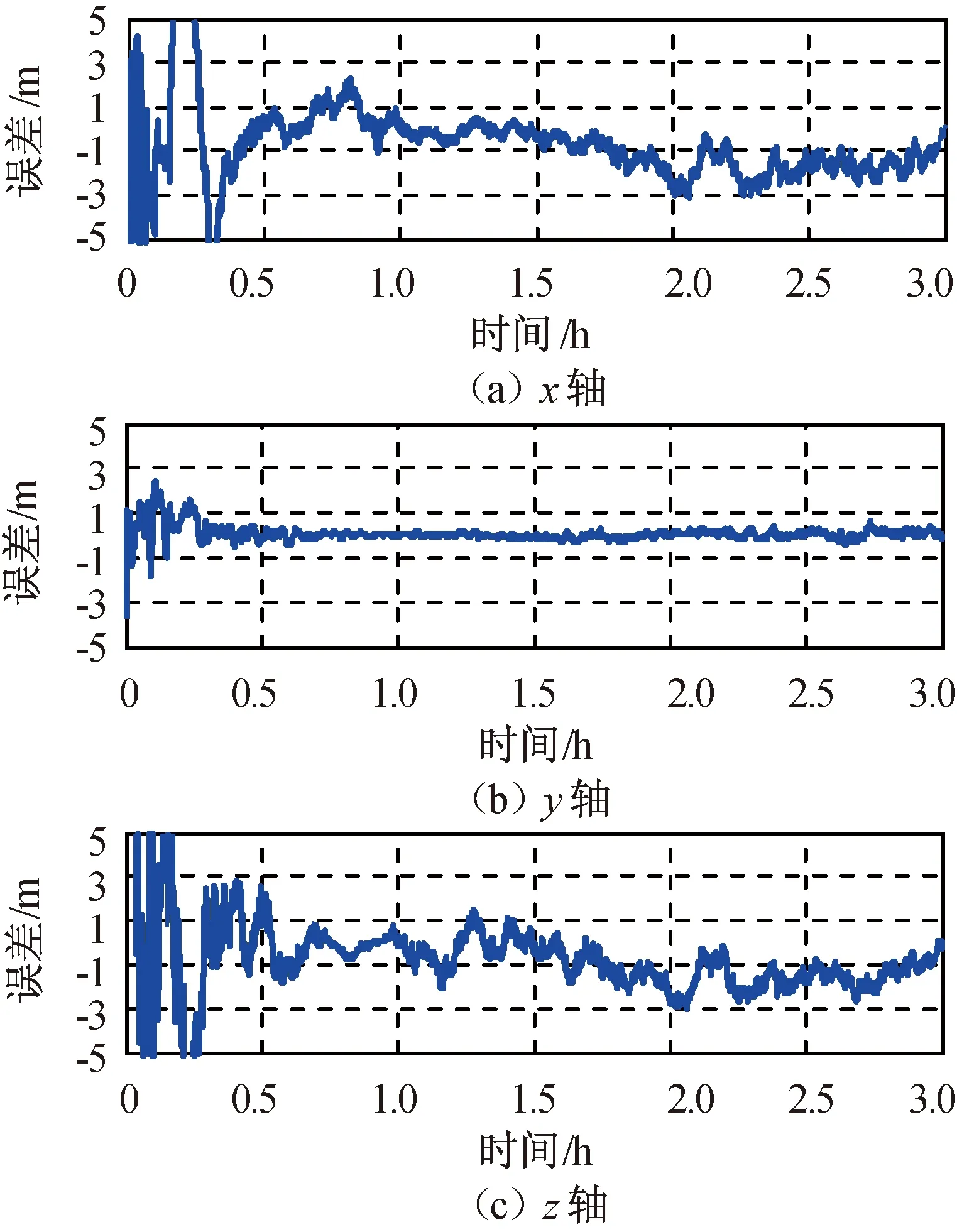
图5 目标飞行器轨道系中相对位置误差Fig.5 Relative position error in target orbit coordinate

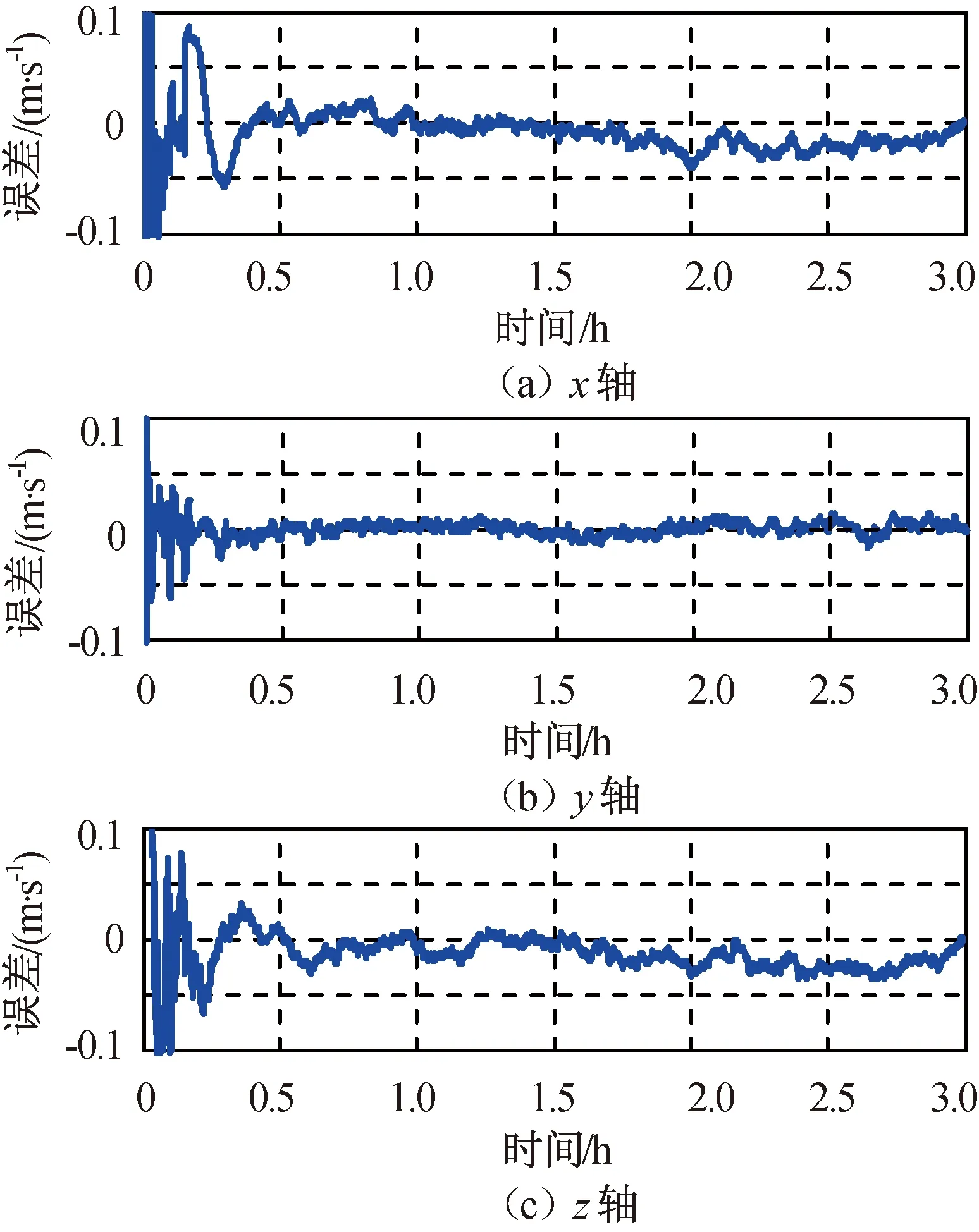
图6 目标飞行器轨道系中相对速度误差Fig.6 Relative velocity error in target orbit coordinate

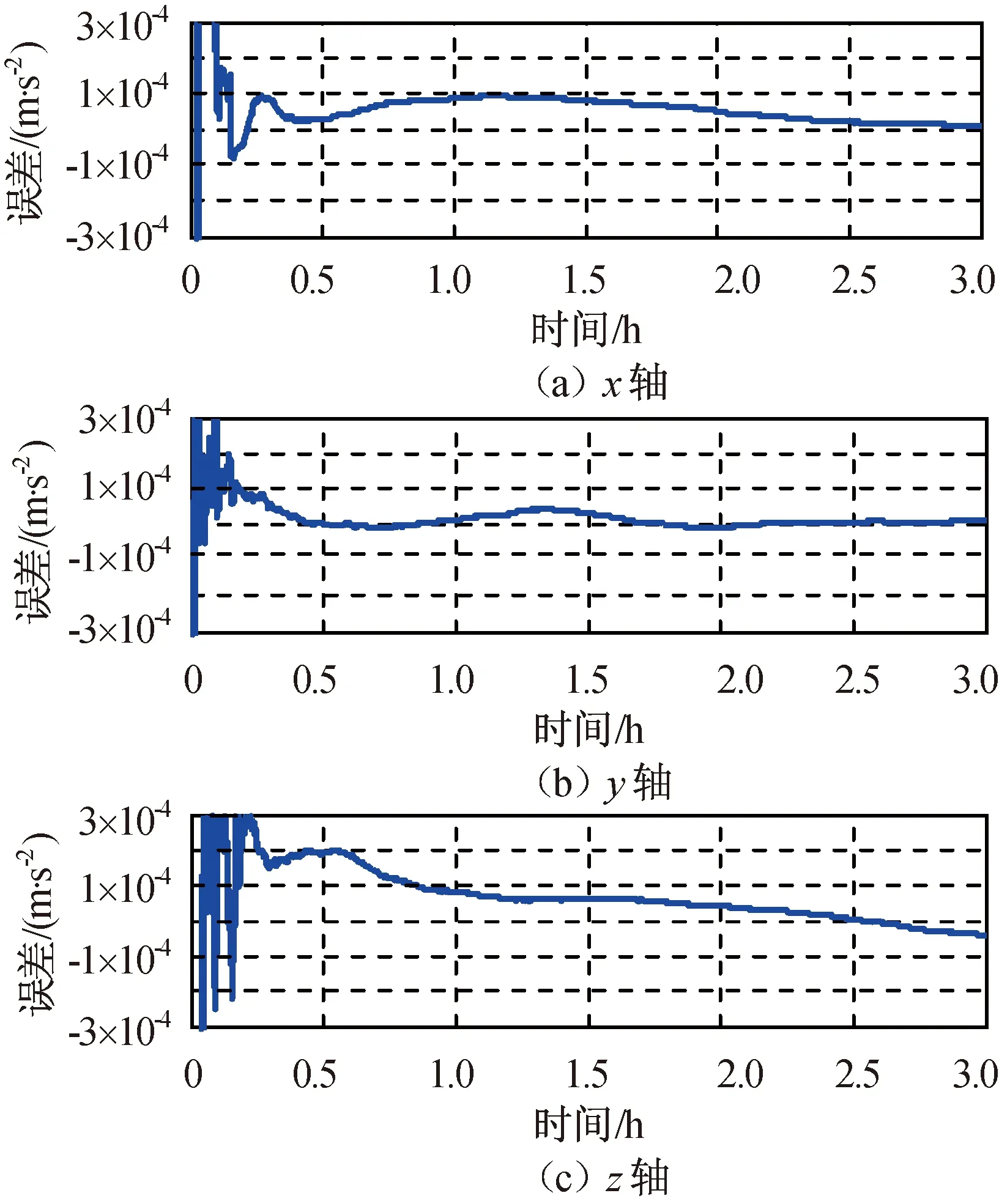
图7 相对导航滤波器的加速度计常值偏差估计误差Fig.7 Estimate error of accelerometer constant warp of relative navigation filter

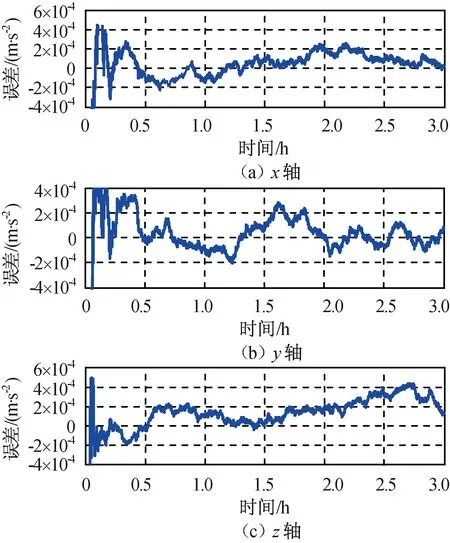
图8 绝对导航滤波器的加速度计常值偏差估计误差Fig.8 Estimate error of accelerometer constant warp of absolute navigation filter

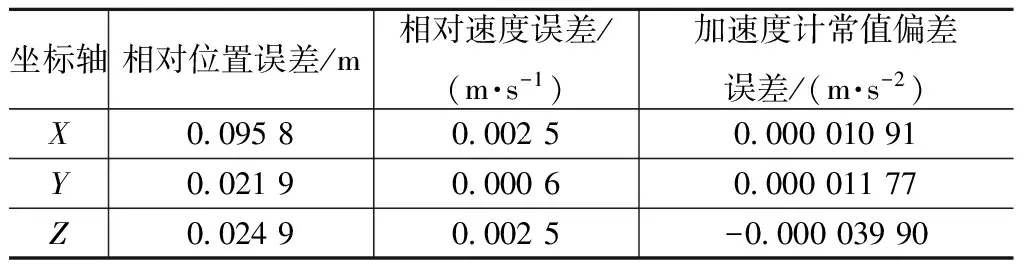
坐标轴相对位置误差/m相对速度误差/(m·s-1)加速度计常值偏差误差/(m·s-2)X0095800025000001091Y0021900006000001177Z0024900025-000003990

5 结束语

本文对基于激光测距和惯导的非合作目标远程交会相对导航算法进行了研究。设计了相对导航系统，给出了相对导航算法及相应的数学模型。根据激光测距仪输出的相对距离和相对方位、俯仰角，对惯导得到的姿态、位置信息用卡尔曼滤波获得相对位置与速度的误差，并对递推结果进行修正。研究和数学仿真发现：在远程交会结束时刻，本文相对导航方法的相对位置误差小于1 m，相对速度误差小于0.05 m/s；相对导航滤波器的加速度计常值偏差估计误差明显小于绝对导航滤波器。本文提出的相对导航方法，适于非合作目标远程交会，在工程中有较好的参考价值。

[1] 杨雪勤， 王洪宇， 冯刚. 失效卫星救援过程中相对导航算法研究[J]. 上海航天， 2015， 32(4)： 1-7.

[2] BRYAN T C. Automated capture of spacecraft[R]. AIAA, 93-4757, 1993.

[3] 赵春慧， 李仕海. 远程导引脉冲方案的有限推力修正[J]. 上海航天， 2014， 31(1)： 18-21+36.

[4] KAWANO I, MOKUNO M, KASSAI T, et al. Results and evaluation of autonomous rendezvous docking experiments of ETSVI[R]. AIAA, 99-36780, 1999.

[5] PARK Y W, BRAZZELL J P, JR CARPENTER J S, et al. Test results from real-time relative global positioning system flight experiment on STS-69[R]. NASA, TM 104824, 1996.

[6] CLARK F D, SPAHAR P T, BRAZZELL J P, et al. Laser-based relative navigation and guidance for space shuttle proximity operations[R]. AAS, 03-014, 2003.

[7] GAYLOR D E, LIGHTSEY E G. GPS/INS Kalman filter design for spacecraft operating in the proximity of the international space station[R]. AIAA, 2003-5445, 2003.

[8] WOFFINDEN D C, GELLER D K. Relative angles-only navigation and pose estimation for autonomous orbital rendezvous[J]. Journal of Guidance, Control, and Dynamics, 2007, 30(5): 1455-1469.

[9] HABLANI H. Autonomous inertial relative navigation with sight-line-stabilized integrated sensors for spacecraft rendezvous[J]. Journal of Guidance, Control and Dynamics, 2009, 32(1): 172-183.

[10] CREAMER N G. Multiple quantum well retromodulators for spacecraft-to-spacecraft laser interrogation, communication and navigation[C]// 15th AIAA/USU Small Statellite Conference. Logan, AIAA, 2001: SSC01-V1-6.

Study on Noncooperative Target Long-Distance Rendezvous Relative Navigation Based on Laser Distance Measurement and Inertial Navigation

YANG Dong-chun1, ZHAO Chun-hui2, GU Dong-qing2

(1. Shanghai Academy of Spaceflight Technology, Shanghai 201109, China; 2. Aerospace System Engineering Shanghai, Shanghai 201109, China)

A relative navigation method based on laser distance measurement and inertial navigation was studied for long-distance rendezvous of noncooperatiive target in this paper. The relative navigation system was given out which composed of laser distance measurement instrument and inertial units. The algorithm of relative navigation was designed. Relative distance and azimuth and pitching would be gained from laser distance measurement. The attitude and position of source satellite would be gained from inertial navigation. The relative orbit dynamics equation could be deserved. Meanwhile, the relative position and velocity from the equation were gained. And the relative distance, relative azimuth and pitching, the attitude and position of source satellite were acquired. The error of relative position and velocity could be gained by Kalman filtering. The real navigation message from the error and the solution of relative orbit dynamics equation was acquired. The simulation results showed that this relative navigation method was suitable to long-distance rendezvous of noncooperatiive target. The error of the relative distance was less than 1 m and the error of the relative velocity was less than 0.05 m/s as well as the estimation error of the constant drift for the accelerometer of the relative navigation filter was smaller than that of the absolute navigation filter at the end of long-distance rendezvous.

Noncooperative target; Long-distance rendezvous; Relative navigation; Laser distance measurement; Inertial navigation; Relative orbit dynamics; Relative distance; Relative attitude; Kalman filtering

1006-1630(2016)04-0075-06

2015-12-22；

2016-05-09

杨东春(1975—)，男，高级工程师，主要研究方向为新型航天器总体设计。

V448

A

10.19328/j.cnki.1006-1630.2016.04.013