狭缝型分布板流化床提高核桃壳颗粒的流化效果

李占勇，王少铁，王 娟，张建国

（1. 天津科技大学机械工程学院，天津 300222；2. 天津市轻工与食品工程机械装备集成设计与在线监控重点试验室，天津 300222）

狭缝型分布板流化床提高核桃壳颗粒的流化效果

李占勇1,2，王少铁1，王 娟1，张建国1,2

（1. 天津科技大学机械工程学院，天津 300222；2. 天津市轻工与食品工程机械装备集成设计与在线监控重点试验室，天津 300222）

为了提高Geldart D类大颗粒物料在流化床中的流化效果，该文设计了一种结构简单的狭缝型气体分布板，进行了核桃壳颗粒（2～2.8 mm）的流态化试验，结果表明狭缝型分布板比传统多孔分布板提高床层膨胀率约5%，降低最小流化速率约8%。在欧拉-欧拉法的双流体模型和颗粒动力学理论基础上，建立流化床内气固两相流的数学模型并对模型进行验证，模拟值与试验值的误差在8%以内。利用数学模型对2种分布板流化床内大颗粒流化过程进行数值模拟，比较了2种分布板结构对流化床内床层压降、床层膨胀率、颗粒相体积分数及气固两相的流化速度的影响。模拟结果表明：狭缝型分布板的“V”型气流通道结构，使得气流易于集束向上运动，形成大气泡对床层造成扰动，从而增大床层压降波动幅度，提高床层膨胀率，并在流化床内形成4个小环流，促进气体相和颗粒相之间的混合，使得核桃壳颗粒流化均匀。该研究为大颗粒物料处理过程中流化床分布板的设计和选用提供参考。

流态化；模型；设计；气体分布板；大颗粒；模拟

0 引言

流化床具有高效的传热传质、均匀的温度场、较大的处理量以及能够实现连续性操作等优点，已得到人们越来越多的关注，并且在能源、化工等工业领域得到广泛应用。根据Geldart[1]的研究，气固流化床中，粗颗粒和细颗粒的流态化特性有明显的差异，从而根据颗粒的密度和直径将流态化的颗粒分为A、B、C、D 4类，其中A、B两类颗粒易于流化，而C类颗粒由于粒子间的黏着力，流化状况差。D类颗粒指过粗颗粒或喷动用颗粒，平均粒度在0.6 mm以上，由于粒径较大，临界流化速度也较大，难以流化，且流化时容易产生极大气泡或出现节涌现象，使操作过程难以稳定进行。

近年来，随着对生物质利用的重视，运用流态化技术对大颗粒物料（如生物质）进行干燥[2]、燃烧[3]、气化[4-7]、热解[8]等的研究和应用逐渐兴起。为了提高流态化技术对大颗粒物料进行处理的适应性，研究者们从流化床形式（有无振动）、气体操作参数（气体速度、温度等）、流化床的床体结构和内构件以及流化辅助方式（在大颗粒中添加其他易流化颗粒、采用脉动辅助流化等）等方面进行了试验研究。杨国华等[9]以粒度分布较广的大颗粒为对象，研究了大颗粒振动流化床的空气动力学特性，得出了大颗粒振动流化床的三层结构特征，并探讨了振动对大颗粒流化床的流化参数的影响规律。李晓光等[10]以黄豆、绿豆及小米模拟水泥生料球，探讨了大颗粒流化过程中的鼓泡及节涌现象，并通过床层内压力脉动的测定研究了大颗粒流化床的流化质量，认为粒度分布是影响流化质量的重要因素。Hilal 等[11]研究了分布板类型、分布板几何尺寸和床径对最小流化速度的影响，结果表明，最小流化速度随孔斜角的增大而减小。王萍等[12]降低了锥形气体分布器的安装高度并在锥形进气管的底部圆周上均匀开设6个120 mm×60 mm的方孔，通过对气体分布器安装位置的调整和锥形进气管底部的改动，有效地改善了反应器底部气流的分布，缩小并消除了低速区域，使气流能够较均匀地进入流化床层，固体颗粒沉积现象得到有效改善。Włodzimierz[13]设计了适应于生物质干燥的新型气体分布板。Sachin等[14]针对流化床干燥器设计了有效的气体分布装置。此外，李占勇等[15-16]通过添加小颗粒以改善大颗粒的流化特性，并且采用脉动气流辅助该双组分体系颗粒的混合。

同时，由于大颗粒两相流动的特殊性及试验方法的局限性，造成难以真正掌握大颗粒流化床内气固两相运动特性的本质，许多研究者采用数值模拟手段对大颗粒流化过程进行仿真研究。Assari等[17]用粒径为3 mm的颗粒进行模拟与试验，研究了气体进口速度和温度对床内含湿量、颗粒温度等的影响，得出模拟与试验的结果能够较好的吻合。Kawaguchi等[18]和Tsuji等[19]对二维流化床中节涌、鼓泡以及快速流化过程中床内絮状物的形成和解体等现象进行了模拟研究，模拟结果与定性的试验分析较吻合，但是与实际情况还存在着一定的差距。Sharma等[20]采用欧拉法研究了三维气固流化床内的脱泡时间和速度场分布情况，模拟计算结果与试验测量值之间的误差在10%之内。Ahuja等[21]研究了表观气速、床内有无管道及布风方式对大颗粒流动的影响。还有部分学者对生物质流化床的反应过程进行了试验和数值模拟研究[22-23]。

分布装置是流化床的重要组成部分，其工作性能直接影响流化床内气固两相的混合流动和化学反应过程。然而，目前关于流化床分布板结构和分布板种类开发的研究还相对较少。本研究的目的是开发一种结构简单、制造加工容易、气体分布均匀的狭缝型流化床气体分布板，用以提高D类颗粒在流化床中的流化性能。以核桃壳为试验物料，进行狭缝型分布板和传统多孔型分布板时核桃壳颗粒（2～2.8 mm）的流化动力学特性试验，研究狭缝型分布板提高大颗粒物料的流化效果。建立流化床内气固两相数学模型并进行数值模拟，以研究狭缝型分布板结构提升大颗粒流化效果的机理。以期为大颗粒物料处理过程中流化床分布板的设计和选用提供参考。

1 试 验

1.1 试验装置

试验装置流程图如图1a所示，最主要部分为矩形流化床（自制，尺寸285 mm×190 mm×700 mm）。罗茨风机（YJ3LR，美国，Gardner Denver）的标定最大输出为420 m3/h，产生的气体由阀门调节控制流量，经过转子流量计（LZB型，流量0～600 m3/h，中国，天津市五环仪表厂）测定显示流量后进入流化床。U型管压差计（BY-U型，中国天津市塘沽玻璃仪器厂）用来测量床层压降，U型管一端接在分布板上方，另一端接在流化床顶部无颗粒区（如图1a），压差计的读数即为床层压降。床层膨胀高度采用目测法，流化床床体上有安装标尺，试验过程中通过多次测量读取床层高度的波动范围，求取波动的平均值及上下偏差，以减小测量的误差值。

本文用到的狭缝型分布板由多块角钢焊接而成，形状类似瓦楞结构（如图1b所示），根据开孔率5.6%[24]计算（本次设计的狭缝型气体分布版的开孔率为5.6%）得角钢间的狭缝宽度为2 mm，狭缝个数为8条，均匀分布于分布板上。作为对比的传统多孔板的开孔率同为5.6%，开孔呈正四边形均匀分布，孔径2 mm，孔数966个。

1.2 试验物料

本文所采用的固体颗粒是农业废弃物核桃壳，经粉碎后为片状颗粒，用泰勒标准筛（8～10目）进行筛选分离，选取筛分直径2～2.8 mm之间的颗粒（属于Geldart D类颗粒）进行试验。

图1 矩形流化床试验装置图Fig.1 Experimental devices of rectangular fluidized bed

1.3 试验结果

初始时分别将狭缝型角钢分布板和传统多孔型分布板接入流化床，装入质量8.5 kg（床层高度均约为200 mm）粒径2～2.8 mm的核桃壳颗粒，打开风机，调节流量控制阀，使流量从120逐渐增大到220 m3/h，每次增加10 m3/h，在不同流量下观察床层的变化情况并读取记录U型管压差计的读数，重复试验3次，求取平均值和标准差。

床层膨胀率是指通入气体后物料层所达到的最大高度与静止状态下物料层高度的比值，它可以反映物料的流化状况或物料的流化剧烈程度。图2为不同分布板时床层压降和床层膨胀率随表观气速的变化，由图可知，在不同气速下，狭缝型分布板的床层膨胀率均大于传统多孔型分布板，且随着表观气速的增大，两者之间的差值先增大后逐渐减小，在气速为0.875 m/s时达到最大。当表观气速为1.128 m/s时，传统多孔型分布板的床层膨胀率为1.49，而相同条件下，狭缝型分布板流化床内的床层膨胀率约为1.56，床层膨胀率提高约5%；表明狭缝型气体分布版更有利于物料的流化和混合。同时，根据最小流化速度确定方法，由图2可知，传统分布板的最小流化速度为0.83 m/s，而狭缝型流化床的最小流化速度约为0.77 m/s，核桃壳颗粒最小流化速度降低约8%。因此可以得出，在相同条件下，物料在较低的气速下就能在狭缝型分布板流化床内实现流化，而且流化程度更剧烈，这不仅有利于物料充分混合，同时也更加节能。

2 模拟研究

试验结果表明，相比传统多孔型分布板，狭缝型分布板更有利于D类大颗粒流化。为了探求狭缝型分布板促进颗粒流化的原因，本文建立了流化床内气固两相流计算流体力学（CFD）模型，分别模拟多孔型分布板和狭缝型分布板下流化床内气固两相流行为并对其进行比较。

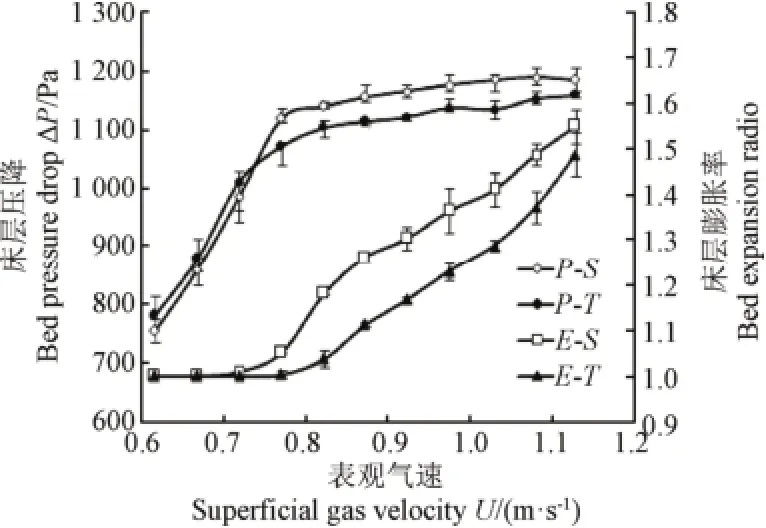
图2 不同分布板床层压降和床层膨胀率随表观气速的变化Fig.2 Variation of bed pressure drop and expansion ratio with superficial gas velocity for different distributors

2.1 数学模型

为了模拟流化床内气固两相的流体动力学行为，本文采用基于欧拉-欧拉法的双流体模型，将颗粒假设为类似流体的连续拟流体，并结合颗粒动力学理论对该过程进行模拟求解。对气体相采用标准κ-ε湍流模型进行描述，颗粒相采用颗粒动力学理论模型进行描述。关于二流体模型的描述详见Vikrant[25]和Goldschmidt[26]，颗粒动力学理论模型的描述详见文献[27-28]。

2.2 计算区域

本文使用商业软件FLUENT 6.3.2®对所设计的流化过程进行计算机模拟研究，物理模型的建立及网格的划分是在其前处理器Gambit程序中进行的。另外基于流化床宽度与颗粒直径之比达到79，远大于20的原因，为了便于计算，本文将流化床简化为二维模型。图3为狭缝型分布板流化床的物理模型，传统多孔型分布板与此类似。物理模型的横向长度和轴向高度分别为285和700 mm。初始时静置床层高度H0为200 mm，固体颗粒体积分数为0.6，气体分布板下方设有高度为100 mm的气体分布室，用以保证气体由床层底部均匀通入流化床内，流化床内无任何内构件。

2.3 边界条件

气体进口为速度入口（velocity inlet），出口为压力出口（pressure outlet），床体壁面及分布板板面设为无滑移壁面边界条件（non-slip wall）。

在流化床进气口（流化床底部），气体流量从120 m3/h增加到220 m3/h，每次增加10 m3/h，则有

式中U为气体表观气速，m/s；Q为气体流量，m3/h；L为流化床长度，mm；W为流化床宽度，mm。可得气体入口速度由0.615逐渐增加到1.128 m/s。气体速度仅垂直于进气面向上，经过气体分布室后均匀地通过狭缝型分布板。在入口处，固体颗粒的体积分数为0。

图3 狭缝型分布板流化床物理模型Fig.3 Physical model of slotted gas distributor fluidized bed

出口边界设为压力出口边界条件，大小为一个标准大气压（绝对压强101 325 Pa），在出口处，各项梯度均为0，即满足

式中T为温度，℃；ν为黏度，Pa·s；ρ为密度g/cm3；ε为空隙率，无因次。

2.4 核桃壳颗粒的物理特性

试验过程中所用物料为粒径（筛分直径）2～2.8 mm的核桃壳颗粒，为了简化计算，模拟过程中将颗粒等效为直径2.4 mm的球形颗粒。颗粒的密度[29]和最大松填充体积分数用浸液法测得，颗粒黏度采用颗粒动力学理论模型进行处理，从理论上推导颗粒相黏性特性及颗粒相应力方程[30-31]。流化气体为常温（25℃）下的空气，气固两相的相关物性参数见表1。

表1 核桃皮颗粒及流化气体的物性参数Table 1 Parameters for walnut shell particles and fluidizing gas

2.5 求解控制

由于所研究的问题属于气固两相流，本文选用欧拉多相流模型来计算两相的动力学行为[32]。选用非稳态隐式求解器，标准κ-ε湍流模型，采用压力速度耦合的SIMPLE算法进行求解计算。时间步长设置为0.0001 s，动量方程、湍动能以及湍流耗散均采用二阶迎风格式进行离散[33]。

2.6 数学模型验证

本文通过比较模拟和试验结果以验证模型的精度。验证试验条件为：狭缝型分布板流化床，静置床层高度约200 mm，核桃壳颗粒粒径2～2.8 mm，气体流量从120 m3/h逐渐增大到220 m3/h，每次增加10 m3/h。图4所示为狭缝型分布板流化床内床层压降及床层膨胀率随气速变化的模拟值与试验值对比情况。由图4可知，随着气速的增大，床层压降先不断增大后维持相对平稳，在固定床状态，由于颗粒充填的关系试验值略大于模拟值，进入流化状态后，模拟值与试验值基本一致。在表观气速约为0.77 m/s后，床层开始松动，之后随着表观气速的增大，床层膨胀率也会不断增大。床层压降及床层膨胀率随气速变化的模拟值与试验值的误差均在8%以内，表明模拟值能够反映床层压降随气速的变化规律并预测床层膨胀高度的演变趋势。在对传统多孔分布板流化特性进行模拟研究时，只是床体结构发生变化，并不影响模型的选择及其计算的精度，故该结论也适用于传统多孔型分布板。

图4 床层压降及床层膨胀率随气速变化的试验值与模拟值对比Fig.4 Experimental value and simulation value comparison of bed pressure drop and bed expansion radio with superficial gas velocity

3 模拟结果及分析

本节主要比较在表观气速为1.128 m/s下，核桃壳颗粒在狭缝型和多孔型分布板流化床内的流化特性的数值模拟结果，主要从床层压降、床层膨胀率、颗粒相体积分数及气固两相的速度等方面进行对比分析，以探讨狭缝型分布板在提高颗粒流化性能的作用和机理。其中，颗粒体积分数为流化床单位体积内颗粒所占体积比例。

3.1 床层压降波动

图5所示为表观气速U=1.128 m/s时流化5～14 s（取样频率为0.1 s）内不同分布板流化床内床层压降随时间的变化情况。进气5 s后，2种分布板流化床内固体颗粒均进入了稳定的流化状态。由图5可知，2种分布板流化床的床层压降均随时间进行不规律的周期波动，且平均床层压降均在1 250 Pa左右，但狭缝型分布板流化床内床层压降的波动振幅要大于传统分布板流化床。在5～14 s内，传统多孔型分布板流化床床层压降波动约为5.5个周期，而狭缝型分布板流化床内床层压降波动约为7.5个周期，即狭缝型分布板内颗粒的波动频率更高。流化床床层压降波动主要是因为床内气泡的产生、并聚和破碎等过程对床层压降产生周期性的影响，如图6a所示。狭缝型分布板流化床内气泡的运动更激烈，因而狭缝型流化床压降波动频率和幅度大。

图5 不同分布板流化床内床层压降波动Fig.5 Pressure drop fluctuations of different fluidized beds

3.2 颗粒相体积分数分布

图6a、6b表示表观气速为1.128 m/s时进气9～11 s 内2种分布板流化床内颗粒相体积分数（颗粒浓度）的瞬时分布云图。颗粒相体积分数较低的区域就意味着气体相体积分数较高，即有气泡正在通过该区域。由图6a、6b可看出流化床内气泡形成、并聚和破裂等过程。气泡一般都在分布板上方形成，多为共生，即在同一时刻的相同床层高度生成多个气泡，气泡在上升过程中将周围颗粒吸入气泡并带动颗粒向上运动（床层中的气泡均含有一定量的颗粒），小气泡逐渐并聚成大气泡，并最终在床层表面发生破裂。结合图5可知，气泡形成、并聚和破裂等过程引起了床层压降的波动。图5中，在9～11 s内，狭缝型分布板流化床的床层压降有2个较明显的波动周期，图6a、6b中可以看到狭缝型分布板流化床内2个完整的气泡生成、并聚和破裂过程，而此时传统孔板流化床的床层压降和气泡运动过程都不是很明显。当气泡在床层表面破裂时，床层压降处于压降波动曲线的波谷，如狭缝型分布板流化床在9.6和10.2 s时，传统多孔分布板在9.8 s时。此后随着新的气泡产生，床层压降又会迅速的上升，如此反复，随着气泡的形成及破裂，床层压降发生着周期性的变化，但变化幅度和频率有所不同。

图6c、6d表示表观气速为1.128 m/s时2种分布板流化床内不同床层高度上的颗粒体积分数（颗粒浓度）的横向分布情况（5～14 s内的平均值），其中H(mm)为床层高度。结合图6a、6b可知，颗粒浓度随床层高度的增加逐渐减小，在低床层区域（如H=100 mm处），颗粒浓度随时间变化的平均值与初始浓度差距不大，但在一些区域由于气泡的产生，颗粒平均浓度在横向位置有所波动。在床层中高部（如H=200 mm处），在某些时刻会出现明显的稀相和密相区分，如狭缝型分布板9.8～10.2 s内，气泡通过区域的颗粒体积分数会明显下降。颗粒平均浓度低于初始浓度，且在横向位置有所波动，但狭缝型分布板的波动幅度要小于传统多孔型分布板，说明在5～14 s内，颗粒在狭缝型分布板流化床内混合的更均匀。在床层高度为300 mm处，传统多孔型分布板流化床内几乎没有颗粒存在了，但狭缝型分布板流化床内还可以看到小量的颗粒，且颗粒集中在床体中心位置处，这说明狭缝型分布板流化床内颗粒能达到的最大高度要高于传统多孔型分布板，即狭缝型分布板的床层膨胀率更大，与试验结果一致。

图7表示的是表观气速为1.128 m/s时两种分布板流化床内不同位置处颗粒相体积分数（颗粒浓度）随时间的波动情况，其中X(mm)为床层横向位置。由图可知，在低床层区域（如H=100 mm处），靠近壁面的位置（X/L=0.15）处，传统多孔型分布板流化床内的颗粒浓度几乎不随时间发生变化，而狭缝型分布板流化床内颗粒浓度会随着时间进行波动；床层中心部位（X/L=0.5处）处，狭缝型分布板和传统多孔型分布板流化床内的颗粒浓度都在进行着周期性的波动，传统多孔型分布板的波动频率大，但狭缝型分布板流化床内的波动幅度大。在床层中高（如H=200 mm处）区域，靠近壁面位置（X/L=0.15）处，两种分布板流化床内的颗粒浓度都在进行着周期性的波动，且狭缝型分布板流化床内得波动幅度更大；床层中心部位（如X/L=0.5处）与低床层区域波动情况类似，即狭缝型分布板和传统多孔型分布板流化床内的颗粒浓度都在进行着周期性的波动，传统多孔型分布板的波动频率大，但狭缝型分布板流化床内的波动幅度更大。以上分析表明，传统多孔型分布板流化床内颗粒浓度的变化主要集中在床体中心区域，而狭缝型分布板流化床内颗粒浓度的变化比较分散。相比于传统多孔型分布板，狭缝型分布板有利于流化床内靠近壁面区域颗粒的流化，使床内颗粒浓度的变化更加均匀，减少靠近壁面区域死角和滞留区的形成。

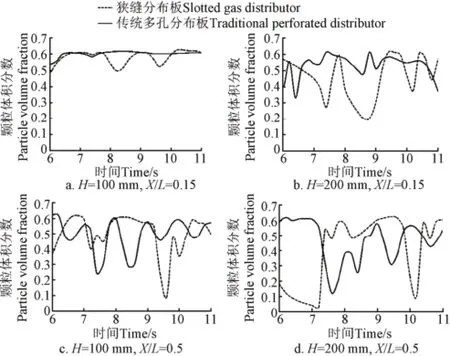
图7 不同分布板流化床内不同位置处颗粒相体积分数随时间的波动情况Fig.7 Fluctuation of particle volume fraction of different positions in different fluidized beds

3.3 气固两相速度分布情况

以分布板为基准，对表观气速为1.128 m/s时气固两相瞬时速度分布情况进行了分析，如图8所示。

图8a给出了9 s（9 s时两种分布板流化床内的床层压降都接近波峰）时不同分布板流化床内颗粒在各个位置上的速度矢量图。由图8a可知，在床层底部（分布板上方），颗粒相的速度矢量方向总体向上，在床层表面处及床体壁面附近，颗粒相的速度矢量方向总体向下，颗粒的流型呈现出一种湾流的特征，包含多个回流，这有利于颗粒相与气体相之间更好的混合[33]。此时，在狭缝型分布板流化床内可以清晰的看到4个小的环流，分布在床层的四个角上，而传统多孔型分布板流化床内则有所不同，流化床内以床层横向中心位置为对称轴形成两个对称的较大环流。环流中心区域一般为气泡通过区，颗粒体积分数较低，而此时图6a、6b中9 s时环流位置处在狭缝型分布板流化床内中可以看到4个气泡，传统多孔型分布板流化床内可以看到2个气泡，两图观察到的情况相符。

图8b给出了9 s时不同分布板流化床内气体在各个位置上的速度矢量图。由图8b可知，气体流经分布板之后，狭缝型分布板的V型气流通道结构限制了气流向四周扩散，因而形成气流喷射，高速气流向上运动并带动床内固体颗粒实现流化。而在多孔分布板流化床内，气流通过圆孔后，向四周扩散，造成速度下降。因此，相比于传统多孔型分布板，狭缝型分布板的V型结构更有利于气流的集束，使气体通过狭缝后垂直向上运动，气流向上穿透能力高。狭缝型分布板的气流集束向上运动，一方面使得在流化床底部区域就形成小气泡（如图6a、6b），对颗粒床进行扰动和混合，同时在床层中部小气泡合并形成大气泡，更能松动颗粒床，提高床层膨胀率；另一方面，在靠近流化床壁面处，气流集束向上运动使得壁面压迫作用相对较弱，多孔板上气流分布均匀（如图8b)，随着气泡运动而形成4个小环流，床层流化更均匀。与狭缝型对比，多孔板上气流过早扩散，一方面，气泡在流化床中部形成，气泡扰动床层作用不如狭缝型；另外，壁面压迫作用较强，使得气流向流化床床层中心集聚，造成两个大环流，均匀性也不如狭缝型。

图8 流化9 s时不同分布板流化床内气固两相各位置上的速度矢量图（U=1.128 m·s-1）Fig.8 Velocity vectors distribution of particle and gas phase at t=9 s for different gas distributors（U=1.128 m·s-1）

4 结论

本文针对用标准角钢制作的狭缝型气体分布板，以核桃壳为试验物料，对设置狭缝型分布板和传统多孔型分布板时核桃壳颗粒（2～2.8 mm）的流化动力学特性进行试验和模拟对比分析。结果表明：

1）床层压降及床层膨胀率随气速变化的模拟值与试验值的误差均在8%以内，表明模拟值能够反映床层压降随气速的变化规律并预测床层膨胀高度的演变趋势。

2）狭缝型分布板比传统多孔分布板提高床层膨胀率约5%，降低最小流化速率约8%。

3）相比于传统多孔型分布板，狭缝型分布板流化床压降波动频率和幅度较大，床层膨胀率更高。床内颗粒浓度的变化比较分散，有利于流化床内靠近壁面区域颗粒的流化，减少靠近壁面区域死角和滞留区的形成。

4）狭缝型分布板的“V”型气流通道结构，使得气流易于集束向上运动，形成大气泡对床层造成扰动，从而增大床层压降波动幅度，提高床层膨胀率，并在流化床内形成4个小环流，促进气体相和颗粒相之间的混合，使得核桃壳颗粒流化均匀。

[1] Geldart D. Types of gas fluidization[J]. Power Technology, 1973, 7: 285－292.

[2] Philippe E, Juray D W. Drying of Biomass Particles: Experimental study and comparison of the performance of a conventional fluidized bed and a rotating fluidized bed in a static geometry[J]. Drying Technology, 2013, 31(2): 236－245.

[3] Pichet N, Vladimir I K. Combustion of palm kernel shell in a fluidized bed: Optimization of biomass particle size and operating conditions[J]. Energy Conversion and Management, 2014, 85(9): 800－808.

[4] Beheshti S M, Ghassemi H, Shahsavan M R. Process simulation of biomass gasification in a bubbling fluidized bed reactor[J]. Energy Conversion and Management, 2015, 94: 345－352.

[5] Ku X K, Li T, Løvås T. CFD–DEM simulation of biomass gasification with steam in a fluidized bed reactor[J]. Chemical Engineering Science, 2015, 122: 270－283.

[6] 范晓旭，贤建伟，初雷哲，等. 生物质鼓泡流化床和循环流化床气化对比试验[J]. 农业机械学报，2011，42(4)：96－99. Fan Xiaoxu, Xian Jianwei, Chu Leizhe, et al. Comparison of bubbling fluidized bed and circulating fluidized bed in gasification of biomass[J].Transactions of the Chinese Society for Agricultural Machinery, 2011, 42(4): 96－99. (in Chinese with English abstract)

[7] 冯飞，沈来宏，肖军，等. 适宜增压流化床操作参数提高生物质热气化气合成甲烷效率[J]. 农业工程学报，2015，31(2)：241－245. Feng Fei, Shen Laihong, Xiao Jun, et al. Improving methane production efficiency from biomass product gas via pressurized fluidized bed system[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(2): 241－245. (in Chinese with English abstract)

[8] 柳善建，易维明，柏雪源，等. 流化床生物质快速热裂解试验及生物油分析[J]. 农业工程学报，2009，25(1)：203－207. Liu Shanjian, Yi Weiming，Bai Xueyuan, et al. Experimental study on biomass fast pyrolysis in fluidized bed and analysis of bio-oil[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2009, 25(1): 203－207. (in Chinese with English abstract)

[9] 杨国华，陈清如，梁春城. 宽分布大颗粒振动流化床流体力学研究[J]. 中国矿业大学学报，1996，25(4)：109－114. Yang Guohua, Chen Qingru, Liang Chuncheng. Study on fluid mechanics of vibrated fluidized bed of wide-sizing large particles[J]. Journal of University of Mining & Technology, 1996, 25(4): 109－114. (in Chinese with English abstract)

[10] 李晓光，徐德龙，肖国先，等. 大颗粒气固流化床的流化特性[J]. 西安科技学院学报，2003，23(4)：425－429. Li Xiaoguang, Xu Delong, Xiao Guoxian, et al. Characterization of gas-solid fluidization with large-particle[J]. Journal of Xi’an University of Science and Technology, 2003, 23(4): 425－429. (in Chinese with English abstract)

[11] Hilal N, Ghannam M T, Anabtawi M Z. Effect of bed diameter, distributor and inserts on minimum fluidization velocity[J]. Chemical Engineering and Technology, 2001, 24(2): 161－165.

[12] 王萍，王书强，孙玉森，等.流化床反应器物料沉积原因分析及结构改进[J]. 齐鲁石油化工，2002，30(1)：68－69. Wang Ping, Wang Shuqiang, Sun Yusen, et al. The reason analysis of material deposition in a fluidized bed reactor and its structure improvement[J].Qilu Petrochemical Technology, 2002, 30(1): 68－69. (in Chinese with English abstract)

[13] Włodzimierz C. Novel Gas Distributor for Fluidized Bed Drying of Biomass[J]. Drying Technology, 2009, 27(12): 1309－1315.

[14] Sachin V J, Arun S, Mujumdar, et al. Design of an efficient gas distribution system for a fluidized bed dryer[J]. Drying Technology, 2009, 27(11): 1217－1228.

[15] 李占勇，潘波，高新源，等. 脉动气流辅助流化下双组分颗粒的混合特性研究[J]. 农业机械学报，2015，46(3)：247－253. Li Zhanyong, Pan Bo, Gao Xinyuan, et al. Particle mixing and segregation of binary mixture in fluidized beds with additional pulsating air flow[J]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(3): 247－253. (in Chinese with English abstract)

[16] Li Z Y, Kobayashi N, Hasatani M. Characteristics of pressure fluctuations in a fluidized bed of binary mixtures [J]. Journal of Chemical Engineering of Japan, 2005, 38(12): 960－968.

[17] Assari M R, Basirat T H, Saffar A M. Numerical simulation of fluid bed drying based on two-fluid model and experimental validation[J]. Applied Thermal Engineering, 2007, 2(27): 422－429.

[18] Kawaguchi T, Tanaka T, Tsuji Y. Numerical simulation of two-dimensional fluidized beds using the discrete element method (comparison between the two-and three-dimensional methods)[J]. Power Technology, 1998, 96(2): 129－138.

[19] Tsuji Y, Tanaka T, Yonemura S. Cluster patterns in circulating fluidized beds predicted by numerical simulation (Discrete particle model versus two-fluid model)[J]. Power Technology, 1998, 95(3): 254－264.

[20] Sharma S D, Pugsley T. Three-Dimensional CFD model of the deaeration rate of FCC Particles[J]. AIChE Journal, 2006, 52(7): 2391－2400.

[21] Ahuja G N, Patwardhan A W. CFD and experimental studies of solids hold-up distribution and circulation patterns in gas-solid fluidized beds[J]. Chemical Engineering Journal, 2008, 143(1/2/3): 147－160.

[22] 李晓伟，刘建坤，王贵路，等. 升温方式对中试鼓泡流化床气化过程的影响[J]. 农业工程学报，2015，31(5)：275－279. Li Xiaowei, Liu Jiankun, Wang Guilu, et al. Effect of heating style on gasification process of pilot scale bubble fluidized bed[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(5): 275－279. (in Chinese with English abstract)

[23] 郭飞强，董玉平，景元琢，等. 生物质流化床气化反应过程数值模拟[J]. 农业机械学报，2013，44(4)：127－130，183. Guo Feiqang, Dong Yuping, Jing Yuanzhuo, et al. Numerical simulation of biomass gasification in fluidized bed[J]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(4): 127－130, 183. (in Chinese with English abstract)

[24] Yang W C. Hand book of Fluidization and Fluid-Particle Systems[M]. chap3.NewYork: Published by CRC Press, 2003.

[25] Vikrant V, Johan T P, Niels G D, et al. Bubble formation at a central orifice in a gas–solid fluidized bed predicted by three-dimensional two-fluid model simulations[J]. Chemical Engineering Journal, 2014, 245(1): 217－227.

[26] Goldschmidt M J V, Kuipers J A M. Hydrodynamic modeling of dense gas- fluidized bed using the kinetic theory of granular flow[J]. Chemical Engineering Science, 2001, 56(1): 571－578.

[27] Wang S, Liu G D, Lu H L, et al. CFD simulation of bubbling fluidized beds using kinetic theory of rough sphere[J]. Chemical Engineering Science, 2012, 71(26): 185－201.

[28] Li Z Y, Su W G, Wu Z H, et al. Investigation of flow behaviors and bubble characteristics of a pulse fluidized bed via CFD modeling[J]. Drying Technology, 2010, 28(1): 78－93.

[29] 郑志峰. 核桃壳树脂化基础研究[D]. 哈尔滨：东北林业大学，2006. Zheng Zhifeng. The basic study on resinification of walnut shell [D]. Harbin: Northeast forestry university, 2006. (in Chinese with English abstract)

[30] 苏伟光.欧拉-欧拉法脉动流化床运动行为模拟[D]. 天津：天津科技大学，2006. Su Weiguang. Euler-Euler Method Simulating Pulsed Fluidized Bed Behaviors [D]. Tianjin: Tianjin University of Science and Technology, 2006. (in Chinese with English abstract)

[31] 沈志恒. 循环流化床颗粒团聚作用的气固两相流动数值模拟[D]. 哈尔滨：哈尔滨工业大学，2010. Shen Zhiheng. Numerical simulation of gas-solid two-phase flow with cluster effect in circulation fluidized bed [D]. Harbin: Harbin institute of technology, 2010. (in Chinese with English abstract)

[32] 李源，杨菁，管崇武，等. 基于CFD的养殖污水净化内循环流化床反应器结构优化[J]. 农业工程学报，2014，30(22)：44－52. Li Yuan, Yang Jing, Guan Chongwu, et al. Optimization for structure of internal loop fluidized bed reactor based on computational fluid dynamics[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(22): 44－52. (in Chinese with English abstract)

[33] Sun D，Wang J Z，Lu H L, et al .Numerical simulation of gas-particle flow with a second-order moment method in bubbling fluidized beds [J]. Power Technology, 2010, 199(3)：213－225.

Fluidization effect of walnut shell particles in fluidized bed with slotted gas distributor

Li Zhanyong1,2, Wang Shaotie1, Wang Juan1, Zhang Jianguo1,2
(1. College of Mechanical Engineering, Tianjin University of Science and Technology, Tianjin 300222, China; 2. Tianjin Key Laboratory of Integrated Design and On-line Monitoring for Light Industry & Food Machinery and Equipment, Tianjin 300222, China)

Gas distributor is a key component in fluidized beds. Various gas distributors for practical application have been successfully developed and studied in depth. Fluidization of coarse particles is still a challenge for good gas-solid contacting. In this study, a slotted gas distributor with simple structure was proposed for the fluidized bed processing coarse particles. The fluidization characteristics of the Geldart D type large particles (2-2.8 mm walnut shell) were investigated experimentally in a 285 mm × 190 mm × 700mm fluidized bed with the slotted gas distributor whose opening rate was 5.6%. The experimental results were compared with the ones obtained from the traditional perforated distributor. It was found that the bed expansion ratio increased by about 5% and the minimum fluidization velocity reduced by about 8% when using the slotted gas distributor, indicating that the slotted gas distributor had better fluidization characteristics for the large-sized particles. To explain the better fluidization performance of the slotted gas distributor, a computational fluid dynamics (CFD) model was developed based on the Eulerian-Eulerian model, the particle kinetic theory, the standard k-ε turbulence model and the SIMPLE algorithm. The CFD model was used to simulate the behaviors of the gas particle flow in the fluidized bed of walnut shell particles with slotted gas distributor or traditional perforated distributor, and the results of experiment and simulation were agreed well. The simulations were conducted under such operation conditions: The physical two-dimensional model of the rectangular fluidized bed was 285 mm × 700 mm with slotted gas distributor or traditional perforated distributor in which the opening rate was 5.6%. Particles packed in the fluidized bed had the volume fraction of 0.6 and the height of the bed was 200 mm. The superficial gas velocity of inlet was selected as operation parameter, which ranged from 0.615 to 1.128 m/s. The simulation results were compared on the bed pressure fluctuations due to bubble formation, the coalescence and eruption, the maximum bed expansion radio, the transient particle volume fraction distribution, the gas/particle velocity vector distribution and so on between the fluidized beds of these two distributors. It was observed that small bubbles first formed close to the gas distributor, coalesced when rising up, and finally erupted near the bed surface, which resulted in periodic fluctuations of bed pressure with different amplitudes and frequencies. Compared with the traditional perforated distributor, the frequency and amplitude of the bed pressure drop fluctuation caused by the slotted gas distributor were bigger and the bed expansion ratio was higher. The change of the particle concentration in the bed was scattered in the fluidized bed with slotted gas distributor, which was beneficial to the fluidization of particles near the bed wall. Also, the dead zone and recirculation area formed near the wall area were reduced. The V-shaped structure of the slotted gas distributor generated strong upward flow jets. The strong jets could deeply reach the material particle bed and easily bring the formation of bigger bubbles. The bigger bubbles caused more intensive disturbance inside the material bed, and thereby the bed pressure drop fluctuation and the bed expansion ratio were improved. Four small circulations were observed to form within the fluidized bed with slotted gas distributor, which was beneficial to the better mixing of gas and particle. Therefore, coarse particles of walnut shell can be well fluidized with the slotted gas distributor. The study provides a reference for the design and selection of fluidized bed distributor in the process of coarse particle processing in fluidized bed.

fluidization; models; design; gas distributor; coarse particles; simulation

10.11975/j.issn.1002-6819.2016.09.032

TH69; TS04

A

1002-6819(2016)-09-0225-08

李占勇，王少铁，王 娟，张建国. 狭缝型分布板流化床提高核桃壳颗粒的流化效果[J]. 农业工程学报，2016，32(9)：225－232.

10.11975/j.issn.1002-6819.2016.09.032 http://www.tcsae.org

Li Zhanyong, Wang Shaotie, Wang Juan, Zhang Jianguo. Fluidization effect of walnut shell particles in fluidized bed with slotted gas distributor[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(9): 225－232. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2016.09.032 http://www.tcsae.org

2015-10-09

2016-03-19

天津市人才引进与科技合作计划国际科技合作项目（14RCGFGX00850）；国家农业科技成果转化项目（2014GB2A100526）

李占勇，男，博士，教授。研究方向：干燥、流态化、热解技术及设备。天津 天津科技大学，300222。Email：zyli@tust.edu.cn