嵌入式轨道钢轨焊接不平顺安全限值研究*

邓永权 凌 亮 肖新标 金学松

(西南交通大学牵引动力国家重点实验室,610031,成都∥第一作者,博士研究生)



嵌入式轨道钢轨焊接不平顺安全限值研究*

邓永权 凌 亮 肖新标 金学松

(西南交通大学牵引动力国家重点实验室,610031,成都∥第一作者,博士研究生)

为调查嵌入式轨道的槽型轨焊接不平顺的安全控制限值及焊接不平顺现代对有轨电车及嵌入式轨道动力作用的影响,建立现代有轨电车/嵌入式轨道耦合动力学模型。计算模型中,现代有轨电车简化为多刚体动力系统，嵌入式槽型轨被视为连续弹性支承基础上的Timoshenko梁,整体道床用三维实体有限元单元模拟,钢轨填充材料用三维粘弹性弹簧-阻尼单元模拟,嵌入式道床板底部的致密混凝土底座及路基简化为等效的弹簧-阻尼单元。基于动力学仿真计算,以GB 5599-1985规定的车辆动力学性能指标为评定准则,对槽型轨焊接不平顺的安全限值进行详细分析。计算结果表明,对于短波波长小于0.2 m的焊接不平顺,1 m范围内槽型轨轨顶面容差的建议控制限值为0.2 mm;对于短波波长大于0.2 m的焊接不平顺,1 m范围内槽型轨轨顶面容差的建议控制限值为0.3 mm。

现代有轨电车; 嵌入式轨道; 焊接不平顺; 轨道不平顺; 控制限值

Author′s address State key Laboratory of Traction Power,Southwest Jiaotong University,610031,Chengdu,China

随着我国城市规模和人口的急剧膨胀,现代有轨电车已成为国内部分城市解决交通堵塞的一种重要的绿色公共交通工具。有轨电车一般行驶于市区内,部分线路区段与道路车辆共享路权,通过采用装有槽型轨的嵌入式轨道结构,实现与道路交通共享路权。

新型嵌入式轨道的槽型轨与道床的连接方式不同于传统的轨道结构中的离散扣件连接方式,它是在混凝土整体道床中设置一个凹槽,钢轨放置在凹槽内,以高分子弹性材料敷设至钢轨的轨头下方将钢轨固定。这一方面大大降低了由于传统离散支承的不平顺性引起的轨道结构振动,另一方面实现了与道路交通的共用路面,因此特别适用于城市有轨电车线路轨道[1-2]。由于现代有轨电车工程在我国刚刚起步,国内针对现代有轨电车与嵌入式轨道结构相互作用及动力特性的研究几乎是空白。基于此,结合我国的工程实际,研究适用于现代有轨电车及其轨道工程相关的重要技术及制定相关标准,对现代有轨电车在我国的快速发展非常重要。

钢轨焊接不平顺是一种常见的轨道几何不平顺,严重的焊接不平顺会引发较大的轮轨冲击作用力,影响车辆与轨道部件的疲劳寿命,甚至可能威胁到车辆的运行安全。国内外学者针对钢轨焊接不平顺的形成和发展机理及防治措施进行了许多有意义的研究工作[3-6]。

到目前为止,国内外钢轨焊接接头平直度验收标准大多是以1 m范围限制最大容差[7-9],比如《铁路轨道设计规范》限制1 m范围内钢轨轨顶面最大容差为0.3 mm,铁建设13号《京沪高速铁路设计暂行、高速铁路轨道施工暂行规定》、TB/T 163.2《焊接接头第一部分：通用技术条件》、法国TGV、韩国京釜高速铁路均建议1 m直尺范围内钢轨轨顶面容许容差为0.2 mm。但上述标准均未对焊接区0 m以下短波不平顺的限值进行规定。

大量的现场调研发现,钢轨焊接区的钢轨伤损现象仍然大量存在(特别是在城市地铁线路上)。焊接区同时也伴随剧烈的轮轨冲击、扣件弹条断裂、轨下胶垫压溃老化、轨枕和轨道板断裂等问题[5]。

此外,目前国内还缺少针对槽型轨焊接不平顺的控制限值标准。嵌入式轨道的结构形式及其所承载的列车载荷与传统的有砟轨道或板式轨道均有较大的差异,故其动力特性及轨道不平顺控制标准也应有所差别。

本文基于现代有轨电车/嵌入式轨道耦合动力学计算,以GB5599—1985规定的车辆动力学性能指标为评定准则,对嵌入式轨道中的槽型轨焊接不平顺的安全限值进行分析,以供嵌入式轨道几何不平顺控制标准制定的参考。

1 动力学计算模型

基于车辆/轨道耦合动力学理论及有限元分析方法[10-11],建立刚柔耦合的现代有轨电车/嵌入式轨道耦合动力学模型,如图1所示。

图1 现代有轨电车/嵌入式轨道耦合动力学模型

图1模型中,三车铰接的现代有轨电车简化为多刚体动力系统,由3个车体、3个转向架构架、2个摇枕、4个传统轮对、2个独立轮组及4个独立车轮共18个刚体组成。每个车体、构架和传统轮对考虑纵向、横向、竖向、侧滚、点头(旋转)和摇头6个方向的自由度。每个摇枕仅考虑摇头自由度,每个轴桥轮组考虑7个自由度,其中2个独立车轮与轴桥共用纵向、横向、竖向、侧滚和摇头5个方向的自由度,而独立车轮的旋转自由度是独立的,整个车辆子系统共有76个独立自由度。

车间铰接机构采用动力学约束建模,车间减振器采用空间非线性阻尼单元模拟。嵌入式轨道由槽型轨、高分子填充材料、轨道板及路基组成。

槽型轨被视为连续弹性支承基础上的Timoshenko梁,整体道床用三维实体有限元单元模拟,钢轨与轨道板间的高分子填充材料用均匀分布的三维粘弹性弹簧-阻尼单元模拟,嵌入式道床板底部的致密混凝土底座及路基简化为等效的弹簧-阻尼单元。

车辆与钢轨间通过非线性的轮轨关系耦合,轮轨空间动态接触几何关系的求解采用一种新型轮轨空间接触几何关系计算模型[10]。

轮轨法向力的计算采用Hertz非线性弹性接触理论求解;而轮轨蠕滑力的计算,先以Kalker线性蠕滑理论计算,轮轨间蠕滑达到饱和后,采用Shen-Hedrick-Elkins理论进行非线性修正[12]。车辆/轨道耦合界面激励模式采用“跟踪窗户”模型[13]。

2 数值计算与结果分析

钢轨连续焊接有效地降低了接头处的轮轨冲击力,从而延长了车轮和钢轨的使用寿命。但由于焊接接头处的焊接材料强度、硬度和微观结构与母材间存在一定的差别,加上焊接钢轨前两端钢轨未对齐,以及手工打磨焊接部分不平所引起的钢轨表面不平顺等原因,线路的焊接接头部分仍然是钢轨表面不平顺的主要形式。

根据日本铁路(JR)对新干线的统计调查以及我国原铁道部科学研究院对焊缝不平顺的观察[7],钢轨焊接区普遍存在如图2所示的焊接接头不平顺形式,其特点是由三段余弦函数构成,可表示为如下位移函数:

(1)

式中:

t——车辆通过不平顺所用时间；

v——车辆运行速度；

δ1,δ2——分别为钢轨焊接接头长波和短波波深,长波波长为1 m；

λ——焊接接头短波不平顺的波长。

为分析嵌入式钢轨焊接不平顺的安全控制限值,首先分析焊接接头不平顺波长及幅值对现代有轨电车/嵌入式轨道耦合系统动力学性能的影响。车辆经过钢轨焊接不平顺位置时,轮轨冲击主要由图2所示短波钢轨焊接不平顺引起,故此处主要分析钢轨焊接接头短波不平顺的波长及幅值对现代有轨电车动力学性能的影响。

图2 焊接不平顺输入模型

计算中车辆和轨道主要参数详见表1[14]和表2。钢轨采用59R2槽型轨,轨面预设有1∶40轨底坡,轨距为1435 mm。考虑直线轨道结构,线路计算长度为300 m,焊接不平顺位于线路标100 m处。焊接不平顺长波波长设为1 m,幅值选为0.1 mm,考虑短波波长λ=0.01～0.50 m,波深δ2=-0.5～+0.5 mm,波深为负值表示上凸型焊接不平顺,波深为正值表示下凹型焊接不平顺;取现代有轨电车最高运行速度v=70 km/h,不考虑常规轨道几何随机不平顺的影响。

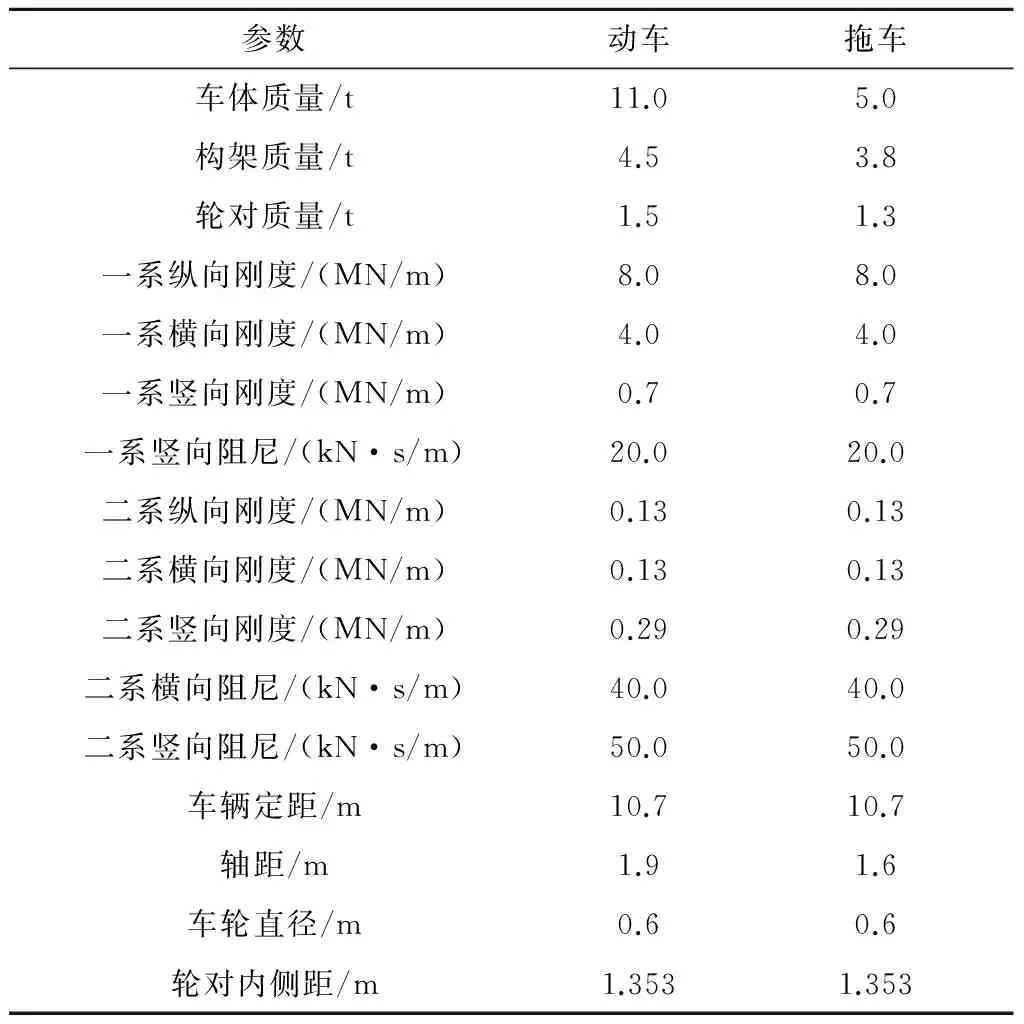
表1 车辆基本参数

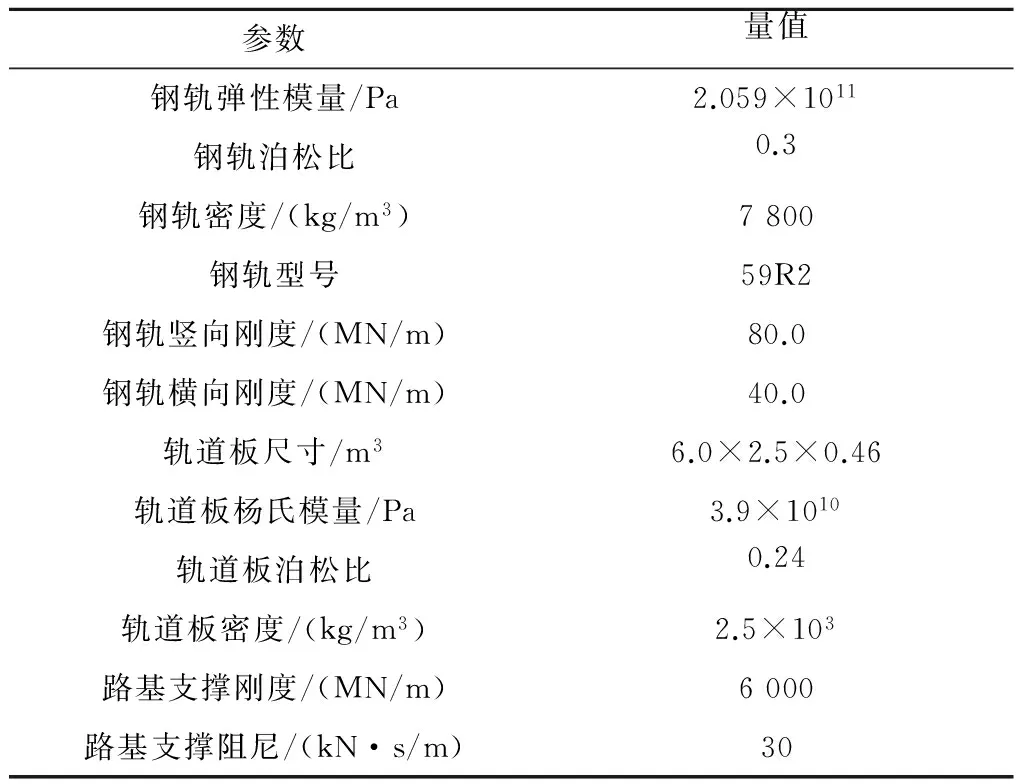
表2 轨道基本参数

图3～图6给出了轮轨横向力、轮轨竖向力、脱轨系数、轮重减载率四项安全性指标随焊接接头波长及和波深的变化规律。由于焊接接头不平顺主要表现为轨面短波几何不平顺,其对车辆的运行平稳性及乘坐舒适性影响不大,故此处未给出车辆运行平稳性指标随焊接接头波长及和波深的变化规律结果。由图3～图6可知:

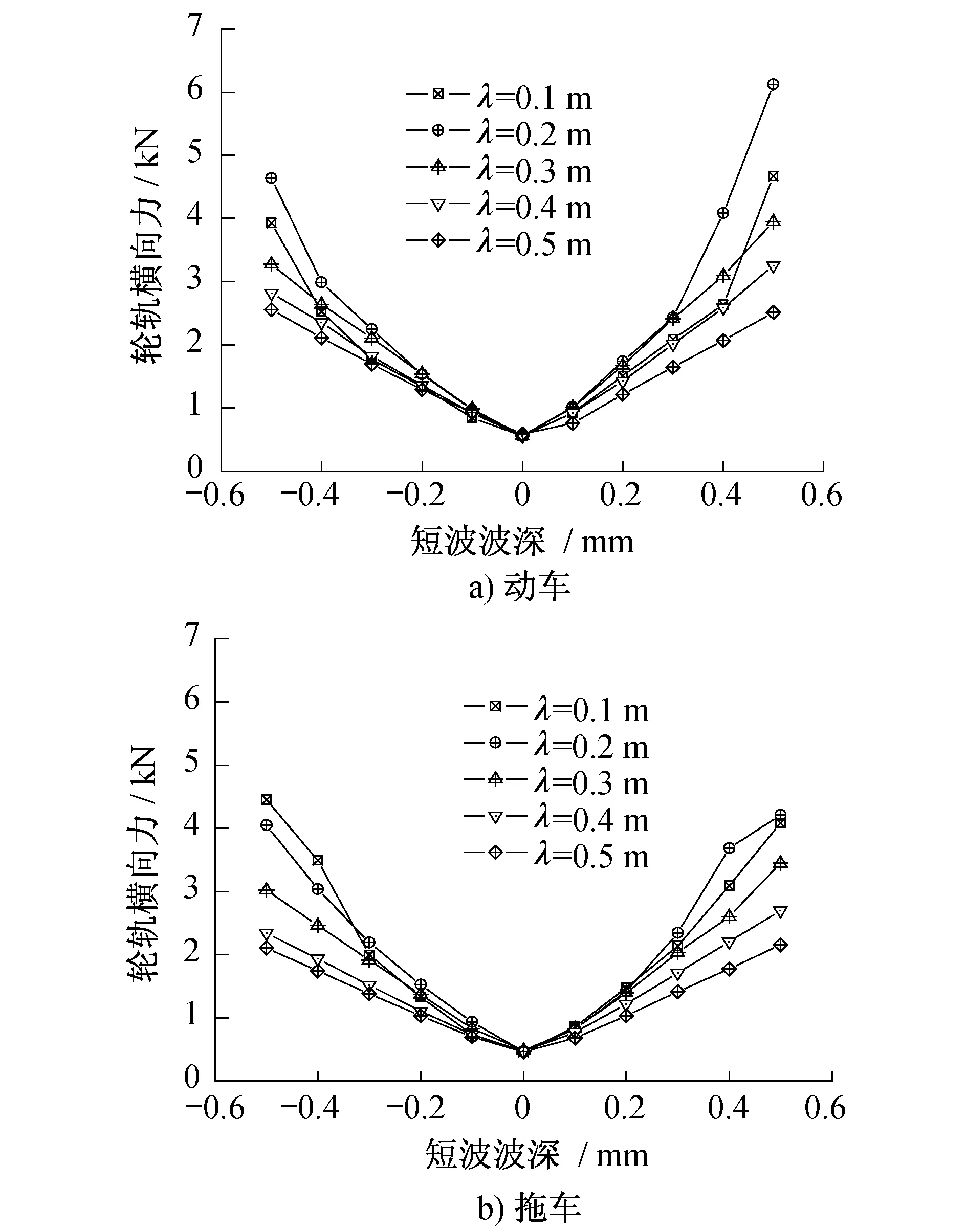
图3 钢轨焊接不平顺短波波长和波深对轮轨横向力的影响

图4 钢轨焊接不平顺短波波长和波深对轮轨竖向力的影响

图5 钢轨焊接不平顺短波波长和波深对脱轨系数的影响

图6 钢轨焊接不平顺短波波长和波深对轮重减载率的影响

(1) 随着焊接接头不平顺波长的不断增加,轮轨横、竖向作用力及脱轨系数和轮重减载率两项车辆运行安全性指标均迅速减小。特别是当焊接接头波长小于0.3 m时,上述四项动力响应指标随波长的变化尤为明显。由此可知,在钢轨焊接接头现场施工和打磨焊接接头时应尽量避免出现波长小于0.3 m的焊接接头不平顺。

(2) 焊接不平顺波深对轮轨相互作用及车辆运行安全性影响明显,焊接接头波长较短时(小于0.3 m),轮轨横向力、轮轨竖向力、脱轨系数、轮重减载率四项动力响应指标与钢轨焊接接头波深呈现出明显的非线性关系;波长较长时,焊接接头不平顺所引起的轮轨冲击载荷及安全性指标响应随波深的增加而几乎成线性增大。

(3) 车辆参数对焊接不平顺激励下有轨电车动力学响应影响显著,动车和拖车动力学响应指标随钢轨焊接不平顺波长和波深的变化规律差异明显;由于动车轴重高于拖车,故动车的轮轨力响应较拖车大,而拖车的安全指标响应明显低于动车。

(4) 嵌入式钢轨焊接不平顺对车辆减载影响最为显著,四项安全性指标中,轮重减载率对钢轨接头波长和波深变化最为敏感。当焊接不平顺短波波深大于0.4 mm时,最大轮重减载率达到1.0,即出现轮轨分离现象。由此可知,嵌入式钢轨焊接不平顺的安全控制限值可由轮重减载率的动态响应及其安全限值确定,如图6所示。

由图3～图6的分析可知,在当前考虑的钢轨焊接不平顺波长和波深范围内,只有轮重减载率的最大值超过其安全限值(GB 5599—1985规定的允许限度值为0.6),而轮轨横向力、轮轨竖向力、脱轨系数三项动力响应指标均未超出各自的安全限值[15]。上述结果也表明,焊接不平顺作用下,现代有轨电车动力响应指标中轮重减载率对钢轨不平顺波长和波深变化最为敏感,嵌入式钢轨焊接不平顺的安全控制限值可由轮重减载率的动态响应及其安全限值确定。

由图7可知,对于短波波长λ=0.1～0.2 m的下凹型复合焊接不平顺,现代有轨电车拖车轮重减载率响应所确定的安全限值约为0.2 mm;对于短波波长λ=0.3 m的下凹型复合焊接不平顺,现代有轨电车拖车轮重减载率响应所确定的安全控制限值约为0.34 mm。

基于图7所示方法,可确定任意波长下嵌入式轨道钢轨焊接不平顺的安全控制限值,如表3所示。

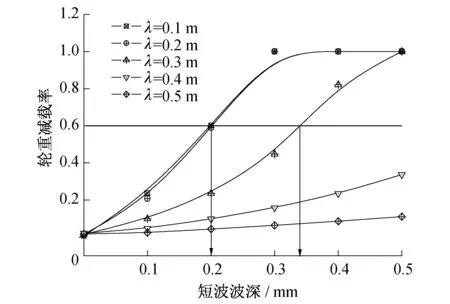
图7 钢轨焊接不平顺安全控制限值分析

表3 不同波长下焊接不平顺建议控制限值

表3中,波深为+表示下凹型焊接不平顺,波深为-表示上凸型焊接不平顺。值得注意的是,表3的建议值也考虑了不同的车辆载重状态(重载和空载)、不同的行车速度、不同车辆参数(动车和拖车)、焊接不平顺控制限值工程应用的可行性及数值计算的误差等因素的影响。

3 结论

基于车辆/轨道耦合动力学理论及有限元分析方法,建立了一种现代有轨电车/嵌入式轨道耦合动力学模型。基于动力学仿真计算,对嵌入式轨道焊接不平顺激励下现代有轨电车的动力响应进行系统分析。其主要结论如下:

(1) 焊接不平顺波长和波深及车辆参数均对现代有轨电车的动力学响应影响显著。

(2) 现代有轨电车动力响应指标中,轮重减载率对钢轨接头波长和波深变化最为敏感,嵌入式轨道焊接不平顺的安全控制限值可由轮重减载率的动态响应及其安全限值确定。

(3) 针对本文计算的嵌入轨道结构及车辆参数,对于不同短波波长的焊接不平顺,给出了1 m范围内槽型轨轨顶焊接不平顺的安全限值。

值得注意的是,基于动力学性能的焊接不平顺控制限值与车辆和轨道的参数密切相关,而本文计算所得的嵌入式焊接不平顺安全限值仅仅基于本文所考虑的计算条件。对于嵌入式轨道焊接不平顺控制标准的制定,则需考虑众多的现代有轨电车车辆类型、嵌入式轨道类型及不同的线路条件。本文所提出的焊接不平顺控制限值计算方法可为今后制定槽型轨焊接不平顺控制标准时提供一种理论参考方法及技术手段。

[1] ESVELD C.Modern railway track [M].Zaltbommel:MRT Productions,2001.

[2] Parsons Brinckerhoff,INC.Track Design Handbook for Light Rail Transit.Second Edition [R].Washington,D.C:TCRP,2012.

[3] 金学松,沈志云.轮轨滚动接触疲劳研究的最新进展[J].铁道学报,2001(2):92.

[4] ZHAI W M,CAI C B,WANG Q C,et al.Dynamic effects of vehicles on tracks in the case of raising train speeds [J].Rapid Transit,2001,215(F2):125.

[5] 李琦.提高钢轨气压焊焊接接头平顺的探讨[J].铁道建筑,2002(12):34.

[6] 周清跃,张银花,陈朝阳,等.秦沈客运专线钢轨的焊接及相关问题 [J].铁道学报,2003(25):114.

[7] 肖广文.钢轨焊接接头伤损分析[D].成都:西南交通大学,2009.

[8] 中华人民共和国原铁道部铁路轨道设计规范:TB 10082—2005/J448—2005[S].北京:中国铁道出版社,2005.

[9] 蔡志鹏,赵海燕,鹿安理,等.钢轨焊接接头平直度的影响因素[J].中国铁道科学,2011(1):20.

[10] 翟婉明.车辆-轨道耦合动力学[M].3版.北京:科学出版社,2007.

[11] 凌亮,肖新标,吴磊,等.地震波频谱特性对高速列车动态脱轨行为的影响[J].工程力学,2013(1):384.

[12] SHEN Z Y,HEDRICK J K,ELKINS J A.A comparison of alternative creep force models for rail vehicle dynamic analysis [J].Vehicle System Dynamics,1983,12(1-3):79.

[13] XIAO X B,LING L,JIN X S.A study of thederailment mechanism of a high speed train due to an earthquake [J].Vehicle System Dynamic,2012,50(3):449.

[14] 李明,戴焕云,丁磊.70%低地板轻轨车建模及动力学分析[J].交通运输工程学报,2004(2):49.

[15] 中华人民共和国铁道部.原铁道车辆动力学性能评定和试验鉴定规范:GB 5599—1985[S].北京:中国标准出版社,1986.

On the Safety Criterion of Welding Irregularities on the Embedded Rail TrackDENG Yongquan, LING Liang, XIAO Xinbiao, JIN Xuesong

In order to investigate in the safety criterion of rail welding irregularities on the embedded rail track and its effects on the dynamics of tram and embedded rail track, a coupling tram vehicle-embedded rail track dynamic model is established. In this model,the tram vehicle is simplified as a multi-rigid-body system with nonlinear suspension characteristics, the grooved rail are modelled as Timoshenko beams with continuous support, while the slabs are modelled with 3D solid finite elements, the filling material that connects the rail and slabs and the elastic subgrade beneath the slabs are assumed to be uniformly viscoelastic elements. The detailed dynamics simulation makes an investigation into the safety criterion of rail welding irregularities on the embedded rail track based on the national railway vehicle dynamics standards (GB5599-85).The numerical analysis shows that the safety limit value of the grooved rail welding irregularities is 0.2 mm in 1m when its wavelength is less than 0.2 m, and the safety limit value is 0.3 mm when its wavelength ranges from 0.2 m to 1 m.

modern tram; embedded rail track; rail welding irregularities; safety criterion

U 213.2+13

10.16037/j.1007-869x.2016.05.007

2014-06-19)

*中央高校基本科研业务资助(2682013BR009)