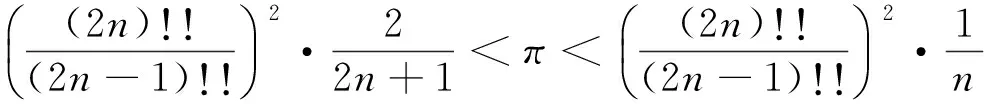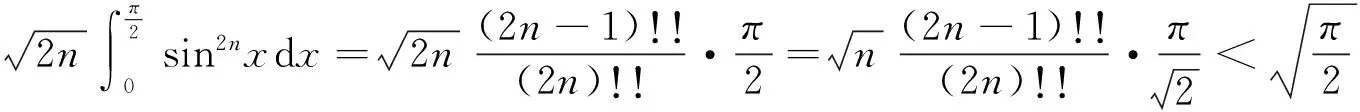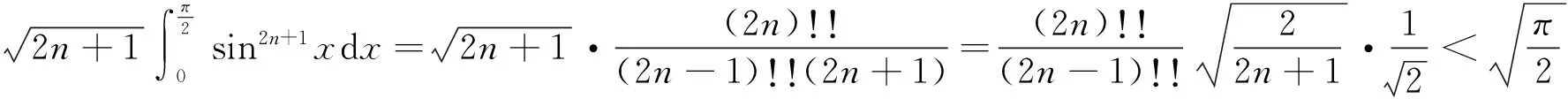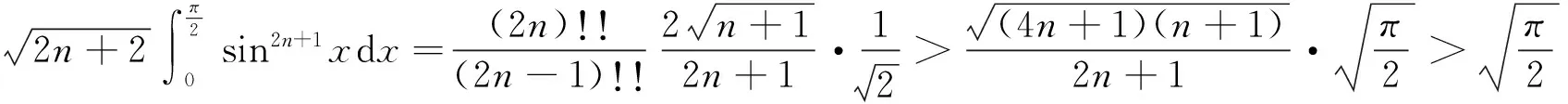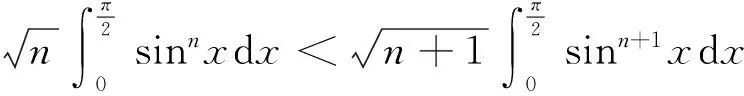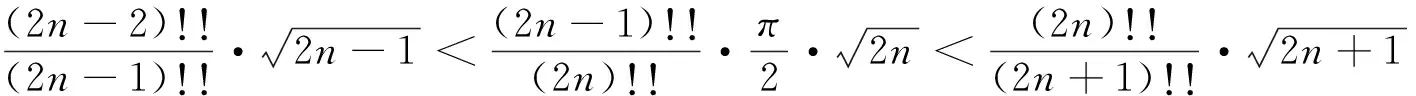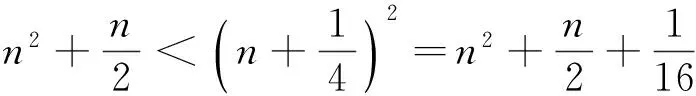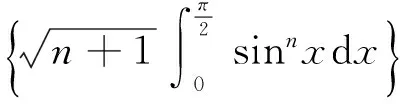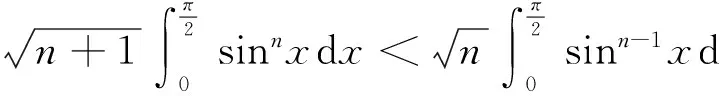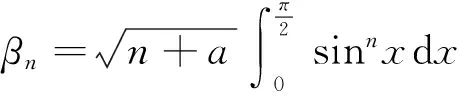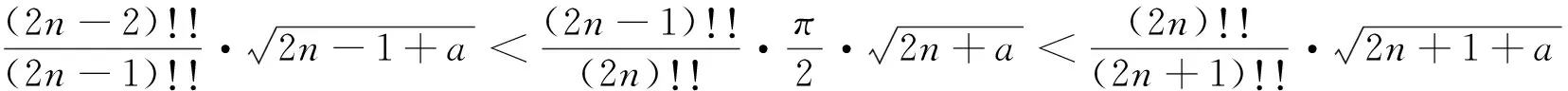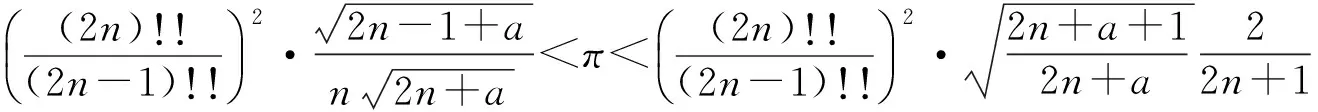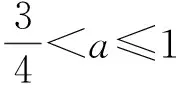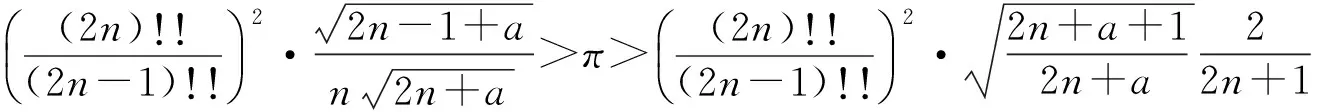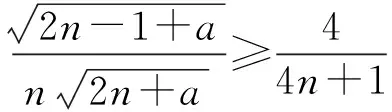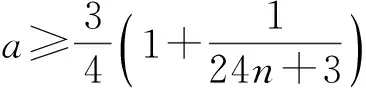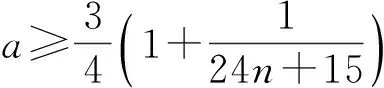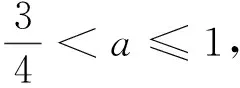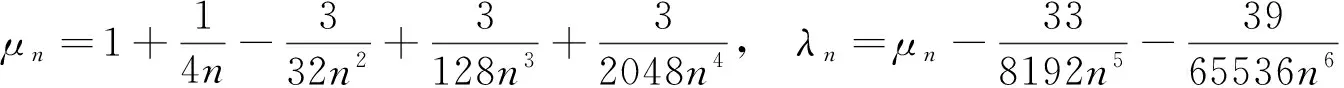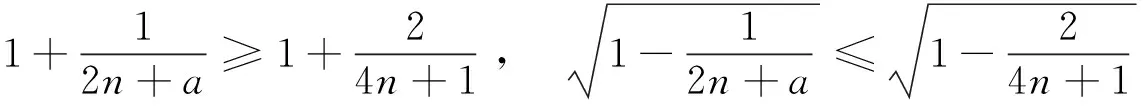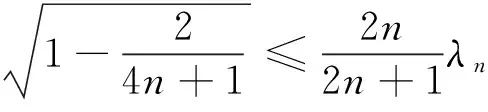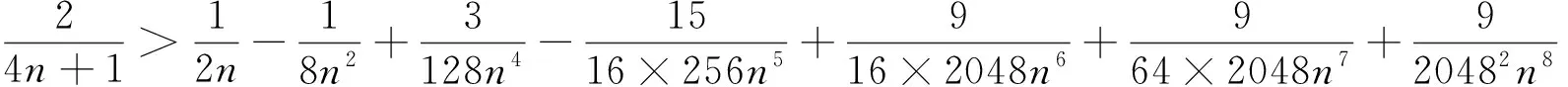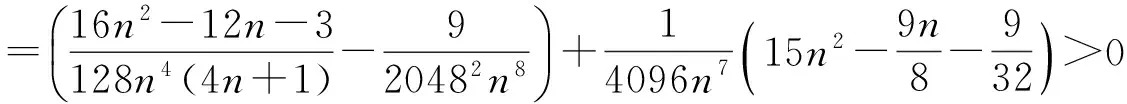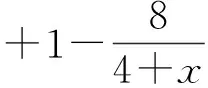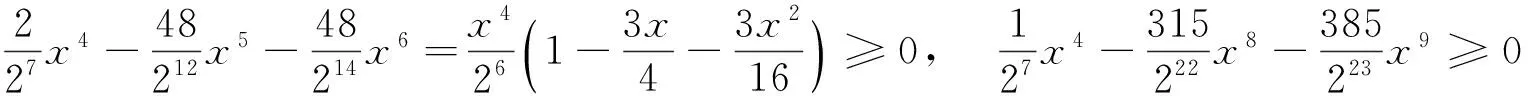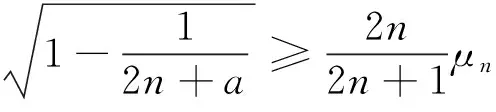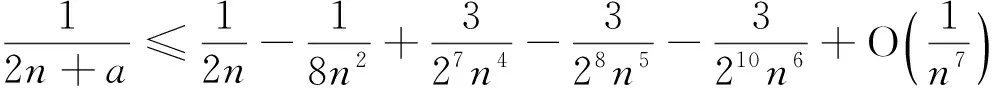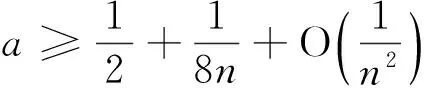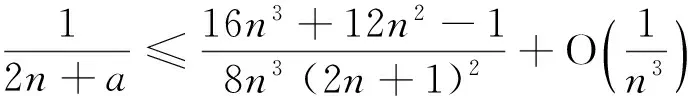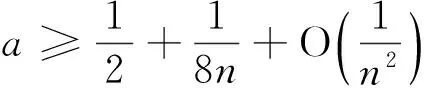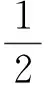与Wallis不等式有关的两个数列的单调性

黄永忠，刘继成

(华中科技大学数学与统计学院， 武汉430074)



与Wallis不等式有关的两个数列的单调性

黄永忠，刘继成

(华中科技大学数学与统计学院， 武汉430074)

利用Wallis 不等式正面回答了《大学数学》 2016, 32(1)：101-104文末提出的猜想，并证明了该猜想的一个推广形式.

Wallis不等式； 单调数列； 夹挤原理

1 问题的提出

文献[1]证明了数列

(1)

的奇数项子列和偶数项子列分别为单调递增数列，数列

(2)

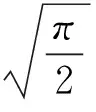
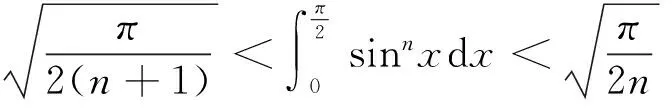
(3)

该文献最后提出猜想：数列(1)为严格单调递增的，数列(2)为单调递减的.本文利用Wallis 不等式对该问题给出正面的回答，并给出文献[1]中所有结论的简化证明.最后，我们证明数列

当0≤a≤1/2时是严格递增的，当1/2

2 结果及证明

回顾基本等式(见文献[2]P230)

(4)

及Wallis 不等式(见文献[2]P231)

(5)

文献[3]得到如下加强版本的Wallis 不等式

(6)

我们将用(5)和(6)来证明本文的结论.

证 由(4)的第一个等式及(6)的第二个不等式可得

由(4)的第二个等式及(5)的第一个不等式可得

因此

由(5)的第一个不等式可得

由(6)的第二个不等式可得

综上，不等式(3)成立.

即要证

亦即要证

由(6)式知第一个不等式成立.

即要证

第一个不等式与前面一样，第二个不等式可由

及(6)式知结论成立.

由定理1、定理2的结论，以及单调收敛定理知，数列(1)和数列(2)都存在极限.事实上，由不等式(3)和夹挤原理立即可得下面的推论.

接下来, 秉承定理2的证明思路将数列(1)和(2)的严格单调性推广到较一般的结论.

定理4 定义

也即证明

(7)

容易直接验证(由2n+a关于a单增知, 仅需验证a=1/4情形)

(8)

由(6)式的第二个不等式及(8)式知，(7)式的第二个不等式成立. 同样，容易直接验证

由(6)式的第一个左边不等式知，(7)式的第一个不等式成立.

(9)

因为

解得

(10)

解得

(11)

(12)

其中

所以由(12)式, 仅需对正整数n分别证明

(13)

和

(14)

对(13)式两边平方, 整理后得到

于是上式左边减去右边, 有

由此得证(13)式.(14)式由下列推算得到

其中

f(x)

因为在区间[0,1]上

所以在区间[0,1]上，有

因此, 定理得证.

证 由定理4的证明过程知, 我们仅需要证明(9)式成立.由(12)式, 仅需分别证明

(15)

和

(16)

经计算，由(15)式平方后得到

于是

(17)

同理，由(16)式平方后得到

由此得到

(18)

[1] 杨天虎，岳志明.两个极限相等的有趣数列[J].大学数学, 2016, 32(1)：101-104.

[2] 华东师范大学数学系. 数学分析(上册)[M].4版.北京：高等教育出版社， 2010.

[3] Gurland J. On Wallis’ formula [J]. Amer. Math. Monthly, 1956, 63(9):643-645.

[4] 周玲.数论中切比雪夫不等式的一点补充[J].大学数学, 2013, 29(6)：39-43.

[5] Lin L. Further refinements of Gurland’s formula[J]. Journal of Inequalities and Applications, 2013, 2013(48): 1-11.

The Monotonicity of Two Sequences Associated with Wallis Inequality

HUANGYong-zhong，LIUJi-cheng

(School of Mathematics and Statistics, Huazhong University of Science and Technology, Wuhan 430074, China)

By using the Wallis inequality, we give a positive answer to a conjecture of the paper published in the journal of the "College Mathematics" 2016, 32 (1):101-104, moreover we obtain a general version of the conjecture.

Wallis inequality; monotone sequence; squeezing principle

2016-04-07； [修改日期]2016-04-26

湖北省教学研究项目(2013052)； 华中科技大学教学研究项目(2015067)

黄永忠(1965-),男，博士，副教授，从事数学分析课程教学研究.Email:huangyz@hust.edu.cn

刘继成(1976-),男，博士，教授，从事数学分析课程教学研究.Email: jcliu@hust.edu.cn

O178

C

1672-1454(2016)05-0076-05