学绩测验分数分布形态及其应用研究*

余 水

(贵阳学院 教育科学学院, 贵州 贵阳 550005)



学绩测验分数分布形态及其应用研究*

余 水

(贵阳学院 教育科学学院, 贵州 贵阳 550005)

从分数分布的偏态系数和峰度系数出发，探讨测验分数分布的类型及其内涵，进而研究分数分布形态的应用现状。研究发现：关于学绩测验分数的分布状态，目前存在对偏态分布概念混淆不清、简单否定偏态分布、盲目遵从正态分布等严重的使用误区。研究结论：盲目遵从分数正态分布可能导致教育的失败。在一般的基于合格测验目的的学绩测验中，应该努力避免出现分数的正偏态分布，理性接受合理的负偏态分布。最后对相关研究的发展趋势进行了简要分析。

学绩测验；分数分布 ；正偏态；负偏态

1 引言

学绩测验，也叫学业成就测验，即学生学习效果的测验，也就是关于学校教学目标的考试[1]169。学校里平时组织的各类考试都属于学绩测验。学绩测验的结果即测验分数，也就是通常意义上说的考试分数，是各级教育行政管理部门、学校教学管理者，以及教师等评价某学科、某课程教学质量的一个重要参考指标。根据经典测验理论和项目反应理论的基本原理，依照学绩测验分数来评价教学质量的工作，主要涉及：测验分数分布的形态、测验的信度、测验的效度，以及测验的难度、区分度等的计算与分析等等。其中，学绩测验分数的总体分布形态可以直观地反映出教学的整体情况。但大多数评价者在分析或评价测验分数的时候，出现过度依赖正态分布理论，且常常以是否正态分布来评价教学的成功或失败。例如：若一个班某门课程期终考试分数呈正态分布，往往被管理者、督学者，甚至教师本人认可；相反,如果某课程测验分数呈现偏态分布(正偏态或负偏态)，该课程的教学往往会被认为存在问题。从教育的根本目的出发，盲目地遵从正态分布、简单否定偏态分布是不正确也是不合理的，对教育、教师、学生均存在许多的不公平。本研究拟从测验分数分布形态的统计指标出发，探讨如何正确认识学绩测验分数的分布形态，并进一步科学合理地指导教学评价过程，最终促进教育测量与评价学的进一步发展。

2 学绩测验分数分布形态的主要统计指标

教育测量学中所说的“测验分数”，也就是统计学中所说的“数据”。分析与统计数据的时候，首当其冲的一个重要概念就是“次数”或“频数”，即某一个数据出现的频次，一般记为f。不同数据的频次的整体情况就是常说的次数分布。检验这个次数分布是否正态分布的方法指标有：皮尔逊偏态量数法、峰度系数法[2]。

2.1 皮尔逊偏态量数

根据数据的平均数与中数、众数的距离，皮尔逊提出一个偏态量数计算公式如下：

偏态系数(SK)用来衡量次数分布是否对称。当SK=0时，表明次数分布图形是左右对称的，次数分布为正态分布；SK﹥0时，表明次数分布图形中右侧有较长尾部，次数分布为正偏态；当SK﹤0时，表明分布图中左侧有较长尾部，次数分布为负偏态。

2.2 峰度系数

峰度系数计算方法如下：

综上，数据次数分布的形态基本由偏态系数和峰度系数就可以确定。在峰度系数一定的情况下，数据的次数分布情况见图1：

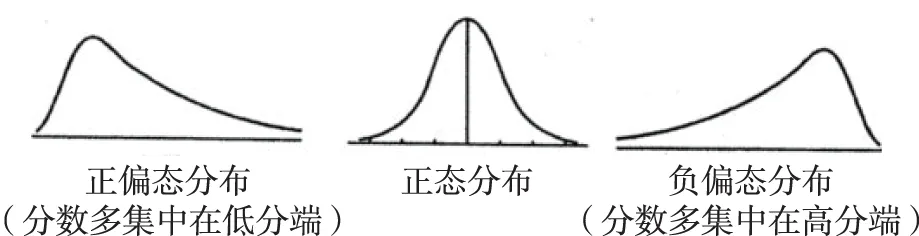
图1 数据次数分布的三类形态示意图Fig.1 Graph of Three kinds of Distribution

2.3 数据次数分布形态在学绩测验中的应用

在教育或心理测量中，经常需要讨论测验难度对测验分数分布的影响。一般来说，在不考虑被试样本特征、教师教学质量、评分标准、评分者心理等因素的前提下，测验的难度会直接影响测验分数的分布情况。具体而言就是：当测验项目的真实难度偏高的时候，正确回答试题的人数就越少，测验分数就越集中在低分端，样本总体的分数分布就越呈现正偏态分布；当测验项目的真实难度偏低的时候，正确回答试题的人就越多，测验分数就越集中在高分端，样本总体的分数分布就越呈现负偏态的分布[1]231；当整个测验的整体难度适中，比如通过率=0.50的时候，样本总体的分数分布就越接近正态分布，即高分和低分都是少数人，大多数人的分数集中在中等水平。因此，除了根据测验整体难度解释测验分数分布形态外，还应该结合被试样本的基本特征、教师教学能力或水平、评分因素等进行综合分析，为学绩测验分数分布的解释提供更多的相关信息，以最终提高教学的综合质量。

3 学绩测验分数分布形态的使用现状

3.1 正偏态与负偏态概念的混淆

在实际工作中，有很多教师不知道正偏态或负偏态的概念；即使在高校里，不知道测验分数分布正偏态或负偏态真正涵义的教师也为数不少，就连从事教育、心理专业课程教学的教师也不甚知之。所以，不同教师在给学生讲授正偏态或负偏态相关知识的时候，出现了不同的解释，影响了学生对科学知识的理解。

另外，还有高校专业课程的教材也出现了类似的错误。比如：某应用心理学专业教材《心理测量学》中，关于难度与测验分数分布的原文如下：“……当测验题目过难(即P值过小)时，大部分被试得分会较低，因此被试分数主要集中在左侧低分端，从而使测验分数呈负偏态分布；当测验题目过易(即P值过大)时，大部分被试得分会较高，因此被试得分主要集中在右侧高分端，从而使测验分数呈现正偏态分布……”[3]。这部分知识恰好将正偏态与负偏态的情况弄反了。再如，题为“教考分离试卷的评价与分析”(2011)的研究中，其计算的偏度系数为-0.772，表明分数分布呈负偏态分布，但是接着却解释为“表明多数学生成绩分布在低分端，提示试题偏难”[4]，同样将负偏态的真实含义弄错了。类似错误还见于朱伟民(2006)[5]关于实用试卷成绩统计分析的研究中。

第三，由于网络的普及与便利，很多教师备课时喜欢在百度网页上查找参考资料。不幸的是，关于测验分数的偏态分布，百度网页上也出现了错误。如：“某次测验总分的分布呈负偏态，说明测验整体难度偏难”[6]。再如，百度百科观点“难度水平的确定要考虑及格率，防止损伤学生的自尊心；难度水平的确定还要考虑对分数分布的影响，一般以正偏态为前提，有时候正偏态分布有利于激发学生的学习积极性”[7]，此处“偏态”的正确表述应该是“负偏态”。

出现以上错误的原因，追究起来，还是因为对相关知识的理解停留在“一知半解”的水平，缺乏对科学知识进行深入探究的精神、人云亦云、或是不分良莠地胡乱吸收造成的。

3.2 对测验分数正偏态或负偏态分布的简单否定

作为教育工作者，每一次考试结束后的主要工作就是对考试分数进行分析，以此了解与把握自己教学过程中出现的瑕疵或存在的不足，为下一步努力改进教学方法总结经验，提升教学质量。但在实际工作中，有不少教师，甚至业内有经验的专家、教育管理者等在评价学生学绩测验分数的时候，对分数分布的偏态分布(正偏态或负偏态)现象很不能理解。认为测验分数出现了非正态分布就是有问题的，一定要求整改或查找原因。他们认为，之所以出现偏态分布，肯定是教学的哪一个环节没有做好或者没有达标。如，最近某高校教学质量评估中心对一个地方院校的考试试卷进行评估的时候，直接以“分数分布属于偏态分布”为由，要求地方院校查找原因并进行整改，让考试分数的分布恢复正态分布。

3.3 对正态分布的盲目遵从或过度强调

与上述对偏态分布的简单否定类似的错误是：学生的学绩测验分数分布必须呈正态分布或近似正态分布，主要表现为对测验分数正态分布的盲目遵从或过度强调。如戴培东(1998)[8]在题为“考试分析方法的应用研究”中这样强调正态分布：“……我们认为这次考试近于正态分布，均数为72.5分，离散度和峰度正常，但稍呈负偏态分布。”再如吴明新等(1999)[9]研究指出：“正态分布能够真实反映学生的实际知识、能力水平。若出现正、负偏态分布，就必须从教学大纲、教材内容及命题方面寻找原因……”。再如张云松(2009)[10]题为“综合评价试卷质量分析方法”的研究中，虽然对试卷进行了知识点覆盖面、题量、难度系数、区分度等方面的分析，但也流露出强调正态分布的痕迹。

在心理学中，人类的智力分布的确是正态分布，但不能想当然地认为学生的学绩测验分数也应该归于正态分布。因为影响学生学绩测验分数分布的因素有很多，绝不仅仅受智力因素影响。更严重的是，盲目遵从正态分布，往往会带来意想不到的不良后果。例如，过度追求学生的学绩测验分数的正态分布，会因为忽视学生的真实学习能力而打击部分学生的积极性，影响教学质量的提高；也会人为地套用正态分布而导致测验失去真正的意义。

盲目遵从分数正态分布，强行规定差生，就是要抹杀掉这些学生的任何努力，打上“注定不能合格”的烙印。从这个角度来看，学生学绩测验分数的正态分布实质上反映了教育的失败[11]。布卢姆也说：“我们甚至可以断言: 成绩的分布接近正态分布时, 说明我们的教育是不成功的”。[12]

4 学绩测验分数分布的合理使用

4.1 正确理解学绩测验分数的分布形态

首先是测验的目的决定了测验的分数分布形态。诸如高考这样的选拔性学绩测验，为了便于甄别和选拔，可以增加测验的总体难度，使得学生之间的得分差距拉大，也就是近正态分布。但是，对于各学段内(包括大学)的半期考试、单元测试、期末考试等，则属于合格测验，仅仅是考核学生对所学知识的掌握程度是否达到要求，并不需要拉开学生之间的差距，反而更希望学生的测验分数能呈现负偏态分布，甚至是极明显的负偏态分布。比如某实验学校的某实验班在某门课程的期末考试分数就集中在90分以上，说明该班学生达到优秀的水平，也证明教学实验是成功的，教学是有效的。

其次是测验的真实难度会影响分数的分布。在其他因素均恒定的前提下，难度越大，测验分数自然越低，分数分布极有可能呈偏向左侧低分的正偏态分布，比如奥林匹克数学竞赛测验的分数基本上属于正偏态分布。

第三，其他影响分数分布的因素还有测验样本的同质性或异质性、样本大小等。比如在大学里的期末考试，假如一个20人的班级，期末考试就很难得到正态分布的测验结果。

所以，一刀切地追求学生学绩测验分数正态分布，不仅不可能完全做到，而且其体现出来的是一种错误的教育观念。

4.2 学绩测验分数偏态分布的科学认识

学绩测验分数的偏态分布主要有两种：正偏态与负偏态。所谓正偏态，就是测验分数大多数集中在低分端。学绩测验分数出现正偏态的可能原因有：教师或学生对教学缺乏应有的积极性、教学目标设置过高、测验难度偏高等。例如，某院校某课程的期末考试，连续几届的学生都大面积不及格。当事老师解释说，不是因为我出题偏难了，是因为本课程难度很高，知识很深，学生无法掌握其要领，所以考试分数都不高，而且很多大学的这门课程考试结果都是这样的。从这个老师的解释中，至少可以发现该老师存在以下问题：没有遵循因材施教的理念、明显的教师中心主义、不关注学生学习结果的教书匠风格等。因此，对于大多数的、限于合格测验目的的学绩测验，要尽量避免分数出现正偏态分布。

所谓负偏态，是指测验分数大多数集中在高分端的情况。一般而言，如果学生整体学习能力比较整齐，且都有较好的学习动机与学习态度，那么在一般的合格水平测验中，该批学生的测验分数一定会呈负偏态分布。有研究(张国才，2002)[13]指出，合理的负偏态分布在于两个前提条件：一是教学目标具有合理的难度，二是考试试题具有合理的难度。根据合理的教学目标设计的合理的试卷是成绩负偏态的合理前提。也就是说，只要满足上述两个条件，即使测验分数出现负偏态分布也是合理的。持同样观点的还有李凯丽(2008)[14]在其题为“人体解剖学考试试卷分析与评价”的研究中认为，根据测验的信度、总分的标准差、试卷难度、试题区分度等的分析结果，认为本次测验分数虽然呈负偏态分布，但是该试卷质量是良好的, 成绩的负偏态分布具有其合理性。还有很多其他研究都倾向于认为：学绩测验分数呈负偏态分布，将有利于激发学生的学习积极性。

4.3 将来的研究趋势

在教育实践中，因为学绩测验的分数会受到学科性质、测验环境、教师心理和学生心理等多方面因素的交互作用而导致分数分布出现不同的形态。既不能简单否定学绩测验分数负偏态分布的价值和意义，也不能完全丢掉学绩测验分数正态分布的选拔与甄别功能。出于学绩测验的不同目的，合理追求测验分数相应的分布形态，是必须且科学的。在实际工作中，要明确认识到测验分数正态分布与偏态分布的各种利弊表现，并在此基础上对两者加以有效整合，不断提高学绩测验的真实性和实用性，以促成全体师生形成正确的测验观，促进教育的向前发展。例如李金波等人(1998)[15]关于项目难度与被试能力分布最佳匹配的研究中提出：学生能力为正态分布时，其测验项目难度分布的最佳匹配是正态分布；若考生能力为正偏态分布时，则其测验项目难度分布的最佳匹配也是正偏态分布；若考生能力分布为负偏态分布时，则其测验的项目难度分布的最佳匹配也是负偏态分布。

当前，我国教育正处于继续推进改革的进程之中，改革学绩测验分数的评定方式或许可以避免不同分数分布形态所固有的弊端。可以作为将来进一步考虑的测验分数评定形式有：标准分数、等级评定等。例如李翔等人(2011)[16]关于考试成绩分布函数的研究中提出：制定一个合理的成绩分布的要求，然后根据这样的要求构造出标准成绩分布函数，这样的分布是负偏态的，满足实际情况，但是它必须能有效地控制不同分数段的人数，具有一定的区分力度。再根据考试成绩的排名，利用考试成绩标准分布函数换算成相对应的分数。再如张志莉(2011)[17]的关于正态分布在考试成绩评定中的应用研究里提出：运用统计概率相对标准的方法评定成绩的等级，从而能准确评定每个学生在集体中相对位置的高低，便于实事求是地衡量学生的真实水平。

5 研究结论

研究发现，关于学生学绩测验分数的分布状态，目前存在对偏态分布概念混淆不清、简单否定偏态分布、盲目追求正态分布等使用误区。盲目遵从分数的正态分布，不仅不可能完全做到，且其严重后果将直接导致教育的失败。在一般的基于合格测验目的的学绩测验中，应该努力避免出现分数的正偏态分布；同时，理性接受合理的负偏态分布。学绩测验分数的正态分布与偏态分布各有利弊，整合二者优势或者采用新的分数评定方法是将来一段时间内的发展趋势。

[1]朱德全，等.现代教育统计与测评技术[M]. 重庆：西南大学出版社，2003.

[2]张厚粲，等.现代心理与教育统计学[M].北京：北京师范大学出版社，2009：166-167.

[3]戴海琦.心理测量学[M].北京：高等教育出版社,2010：67.

[4]罗汀，黄淑芸.教考分离试卷的评价与分析[J].基础医学教育，2011(11):991-994.

[5]朱伟民.适用试卷成绩统计分析[J].中国教育技术装备，2006(5)：13-15.

[6]百度作业帮.负偏态分布[EB/OL](2014-10-09)[2015-11-28]http://www.zybang.com/question/80a081e05effc9869706024769c95104.html.

[7]百度百科.试题难度系数[EB/OL] [2015-11-28]http://baike.baidu.com/link?url=RpWChoBai9Clcb-GFZ8N05IYvyG7IfMU9DyPwTY9PGJ5qyg0WjQG4X_l7ugbNFUnedo3Ck_oGpoR3BK-bwJ1w_ .

[8]戴培东.考试分析方法的应用[J].中医教育，1998(4)：24-26.

[9]吴明新，宋涟钟.论考试成绩的统计与分析[J].江苏商业管理干部学院学报，1999(3)：80-82.

[10]张云松.综合评价试卷质量分析方法[J].数理统计与管理，2009(2)：232-236.

[11]蒋波.正态分布的使用误区及影响因素[J].浙江教育科学， 2006(4):26-27.

[12](美)布卢姆.教育评价[M].邱渊，等，译.上海：华东师范大学出版社, 1987：74.

[13]张国才.学生学习成绩负偏态分布的合理性[J].江苏高教，2002(2)：74-76.

[14]李凯丽.人体解剖学考试试卷分析与评价[J].医学教育探索， 2008(7)：679-681.

[15]李金波，王权.项目难度与被试能力分布最优匹配的模拟研究[J].心理学报，1998(2)：197-202.

[16]李翔，冯珉，等.考试成绩分布函数特点研究[J].中国科学技术大学学报，2011(6)： 531-534.

[17]张志莉.正态分布在考试成绩评定中的应用[J].呼伦贝尔学院学报，2011(5)：111-113.

Research On the Distribution and Its’ Application of Achievement Test Score

YU Shui

(Guiyang University Institute Educational Science，Guizhou Guiyang 550005，China)

Began with the Skewness and Kurtosis coefficient of achievement test score, the type and connotation of score distribution, and its’ present situation for application have been studied. Some error for the concept of skewness, simple negation to skewness and false applications with normal distribution have been found. The study suggests that the excessive apply of normal distribution may lead to the fail of education. The negative skewness of test score can be accepted rationally, and the positive skewness must be prevented for some usual test aimed at qualified standard.Finally, some developments has been investigated on score distribution.

Achievement Test; Distribution; Positive Skewness; Negative Skewness

2015-11-17

贵阳学院重点课程“教育与心理统计测量学”建设项目基金(项目编号：20135104)。

余 水(1976-)，男，贵州贵阳人，副教授、硕士。主要研究方向：教育与发展心理学。

G449

A

1673-6125(2016)01-0031-05