基于动态网络的链接分析与预测研究

杨 磊，李臣龙

(1．安徽工程大学 计算机与信息学院，安徽 芜湖 241000；2．安徽工程大学 计算机应用技术重点实验室，安徽 芜湖 241000)



基于动态网络的链接分析与预测研究

杨 磊1,2，李臣龙1,2

(1．安徽工程大学 计算机与信息学院，安徽 芜湖 241000；2．安徽工程大学 计算机应用技术重点实验室，安徽 芜湖 241000)

复杂网络通过新节点和新链接的增加而随着时间快速演化，使用网络的静态特征难以产生精确的链接预测。通过分析动态网络特征，结合张量分解，提出了一种新的基于动态网络的链接预测方法，并应用于真实的复杂动态网络数据集中对未来链接进行分析预测，实验演示了该方法的优点和效果，取得了较好的预测结果。

链接预测；动态网络；张量分析；局部路径

随着在线社交平台和信息网络的增长，复杂静态网络研究在社交网络、信息网络等多方面已经有了大量的研究，并取得了很多成果，但这些研究仅仅关注复杂网络单个快照的静态图属性，缺少网络演化的动态信息[1-2]，而动态网络的影响扩散过程与静态网络有很大不同。现实世界中几乎所有复杂网络都具有某种动态性，其中个体之间的交互随时间推移而不断发生变化。由于链接预测的挑战，通过分析网络中大量节点的增加或减少，抽取随着时间改变的动态信息对于解决链接预测问题是必要的。

动态网络是一种随着时间演化的特殊网络，表示复杂网络在不同时刻的快照，分析每个时刻网络的演化情况，是动态网络研究的重点。目前动态网络研究还处于起步阶段，国内外很多研究人员针对动态网络的各种问题进行探索，很多问题的提出及研究方法都源于静态网络。然而，基于动态网络的时序特点，动态模式挖掘不是各时刻快照上的简单叠加，动态网络在最短路径、聚集系数等指标的全局及局部时序度量方面与静态指标度量有很大区别[2]。Shan 等人[3]依据所考察网络相邻时刻拓扑结构变化不太大的特点，用网络变化增量方式考察每个时刻的社团结构信息，李艳梅等人[4]针对动态信息网络中异常结构演化过程，通过角色定义刻画网络的结构特征，提出了角色演化异常的概念，并给出了基于模式挖掘的角色演化异常发现算法。大多数动态网络模型是基于平均节点度的增长函数[5-6]，在链接预测方面有许多广泛的应用，如基于过去浏览历史预测一个网络冲浪者在一个特定的日子或许会访问的Web页面，预测计算机网络故障的模式，预测一个旅行者在一个特定的月份将要飞往的地方。科学家合作网络是典型的动态网络，随着新作者的加入和原作者间新的合作关系的产生而不断变化，通过研究以前T年的科学会议出版数据，预测作者将会在T+1年在哪次会议发表论文。

本文利用张量分解理论[7]，结合局部路径指标链接预测方法[8]，通过分析包括时间维在内的三维张量网络链接结构，提出了一种动态网络的链接分析预测方法，新的方法应用于真实的动态网络数据集中进行实验分析及评价，并与共同邻居(CN)、Katz指标方法以及EVtCF[9]进行比较参考，取得了较好的实验结果。

1 问题描述

定义1.1(动态网络) 对于无向网络图G(V，E)，其中V是节点集合，E是节点间边的集合，集合{GT，t=1, 2, …, T}是一个动态图，Gt是t 时刻网络拓扑图，GT+1= (V, ET+1)，ET+1是时刻T+1上图的边集。图1是网络在不同时刻的状态变化，节点a和节点b比其他节点活跃，随着时间变化而不断产生新的链接。

图1 网络节点在不同时刻的状态示例

定义1.2 (动态网络链接预测) 给定T时刻动态网络图{ GT, t=1, 2, …, T}，链接预测的问题是推断出下一时刻T+1的图GT+1=(V,ET+1)，其中ET+1是T+1时刻的边集。

为了观察链接关系在时间上的演化趋势，动态网络链接数据可以组织成一个三阶张量。通过分析三维张量链接结构，把时间定义为单独的一维，相应时间t上Z的矩阵切片表示为Zt，通过分析Z的链接结构来预测T+1时刻上的链接。定义一个M*N*T大小的张量如下：

2 张量分析

张量分析首先出现在心理测验学科和化学统计学中，近几年被其他学科领域广泛采用，包括数据挖掘和图分析。张量作为高维数据( 多维数组) 的一种数学表示，一阶和二阶张量分别称为向量和矩阵，张量的阶为三或者更高则称为高阶张量，一个N阶张量是n个矢量空间的乘积。比较典型的张量分解方法有Tucker分解方法、CP分解方法、HOSVD 分解方法等，CP模型在可解释性、解的唯一性和参数的确定方面更有优势。

一个张量Z是由一系列切片组成，每个切片相当于沿着时段T上的邻接矩阵。一个三维CP张量Z可以表示秩1张量之和形式，如图2所示，即向量ak，bk，ck间的外积与权重λk相乘之后的连加和：

(1)

图2 三阶张量的CP分解

其中∘ 表示外积，k为秩1要素的数量，k=1, …, K。λk∈R+，ak∈RM，bk∈RM，ck∈RM，每个被加数λk(ak∘ bk∘ ck)为一个要素，每个向量为一个因子，每个因子矩阵成为来自秩1要素的向量的组合。向量ak，bk，ck进行标准化，假定||ak||=||bk||=||ck||=1，则λk包含了第k个分量的权重。

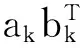
(2)

3 链接预测方法

3.1 三维张量转化二维矩阵

首先把数据存入张量Z，则切片Zt(i, j)表示时间段[tD, (t+1)D]上顶点对i和j之间的链接状态，如果在时间D上链接存在，则为Zt(i, j)=1，否则为0。张量是由一系列Z1到ZT间的邻接矩阵组成，其中下标为时段。为了把数据转换为矩阵X，引入权重θ∈(0, 1)，链接结构考虑时间越近的邻接矩阵，权重越大，则得到公式：

(3)

本文链接预测方法考虑了具有时间因素矩阵中捕获的时间趋势的多重网络快照，其中时间趋势由张量分解获取，采用Holt-Winters方法[10]用来获取张量的时间序列数据。时间序列数据由xt表示，st为x的下一个输出值。序列在时间t=0开始，指数平滑法的最简单形式如下表达式：

s1=x0

st+1=axt+(1-a)st

(4)

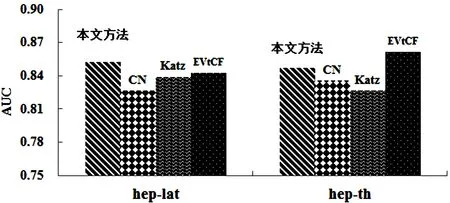
a为平滑因子(0

st+1=axt+(1-a)st=axt+a(1-a)st-1+(1-a)2st-2= axt+a(1-a)st-1+a(1-a)2st-2+…+(1-a)ts0

(5)

从方程3和5可以推导出，预测向量Zt+1用公式表示为：

Zt+1=aZt+a(1-a)Zt-1+a(1-a)2Zt-2+…+(1-a)tZ0

(6)

Zt+1为加权二维矩阵，Zt+1(i,j)表示节点i和j在T+1时刻的链接关系。

3.2 局部路径链接预测

基于路径的链接预测相似性指标有LP指标(Local Path，局部路径)、Katz指标等。LP是在共同邻居指标的基础上考虑三阶邻居的贡献，比CN视野更广，提供了较好的精度和复杂度平衡，是一个比全局测量复杂度相对更低的局部测量。定义如下：

Si,j=A2+εA3

(7)

其中Si, j表示节点i和j相似度分数，值越大，则节点间存在链接可能性越大。A为网络的邻接矩阵，A等价于前文3.1节中的Zt+1，A(i, j)则为节点i和j在时间t+1时刻的链接关系。当节点i和j之间存在链接，则Ai,j=1，否则为0。(A3)xy等于节点x和y间长度为3的不同路径数量。ε是一个可调节参数，用于控制三阶路径的作用，取值为接近于0的很小数字，通过调节ε的值可以获取最高精确度的最优值，对于不同的网络，最优值取值不同。当ε=0而且x和y不是直接链接时，此测量方法退化为CN。

4 实验与评价

4.1 数据集

为了验证所提出的动态网络链接预测算法的性能，本文采用两个合著关系网络数据集作为实验数据，分别是hep-lat(high energy physics-lattice)和hep-th(High Energy Physics-Theory)，数据集来自于大型的科技论文数据库e-print arXiv1，这种网络关系数据广泛地应用于复杂网络的动态结构研究，实验结果与CN、AA以及EVtCF链接预测算法进行对比。每个作者作为一个节点，两个作者之间若有论文合作关系则建立一条边，则表示有链接存在。实验抽取了1992～2010年间的合著关系数据，以年为粒度建立合著网络。相关数据信息如表1所示。

表1 合著关系网络

对数据集使用移动窗口切片方法，把数据划分成训练集和测试集，其中每个训练集包含T=10年的数据，相对应的测试集包含接下来的T+1年也就是第11年数据。训练集中仅保留那些至少10篇出版物的作者(也就是平均下来每年一篇)，每条论文合著记录表示两个作者在相应时间点存在链接。

4.2 实验结果与分析

实验使用Matlab 2012a软件，Intel Core i5-4560处理器，32G内存。实验使用AUC[9](Area Under the Receiver Operating Characteristic Curve)指标来衡量算法精确性，从动态科技论文合著网络中抽取不同时刻数据构成不同规模的网络，每次选取T=10年的数据作为训练集，以T+1年数据为测试集数据计算1次AUC值，然后时间窗口往后移动一年，进行下一次AUC值计算，最后对所有AUC值取平均作为对应时间窗口T取值的链接预测方法的AUC值。

根据训练集上初步测试以及文献资料，设定参数θ=0.2，ε=0.01，本文方法和其他经典算法CN、Katz、EVtCF对比实验结果如上图3所示。从图3可以看出，本文方法在hep-lat数据集上表现最好，在hep-th数据集上表现仅次于EVtCF算法。

图3 链接预测实验效果

5 结论

本文主要针对静态网络忽视网络演化趋势信息的问题，提出了一种基于动态网络的链接预测方法，采用张量分析及Hold-Winters方法，结合局部链接预测方法，以两个真实动态网络数据集进行了实验，实验结果表面，新算法在预测精度方面有所提高。当然，随着复杂网络的高速发展，复杂网络随着时间而不断演化发展趋势及预测仍有待更进一步的深入研究。

[1]陈小强，周丽华，程超，等．动态网络中稳定社区发现[J]．小型微型计算机系统，2015，36(9)：1977-1981．

[2]高琳，杨建业，覃桂敏．动态网络模式挖掘方法及其应用[J]．软件学报，2013，24(9)：2042-2061．

[3]Shan B, Jiang S X, Zhang S, et al. IC: Incremental algorithm for community identification in dynamic social networks[J]. Journal of Software, 2009(20): 184-192.

[4]李艳梅，李川，唐常杰，等．动态信息网络中的角色演化异常及其发现[J]．计算机科学与探索，2015，9(3)：321-329．

[5]李晓东，崔丽娟．大学生网络交往动机与网络行为特点关系研究综述[J]．安徽科技学院学报，2011，25(1)：104-106．

[6]AGGARWAL C, SUBBIAN K. Evolutionary network analysis: a survey[J]. ACM Computing Surveys, 2014, 47(1): 1-35.

[7]ZHAO Qi-bin, ZHANG Li-qing, CICHOCKI A. Bayesian CP factorization of incomplete tensors with automatic rank determination[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(9): 1751-1763.

[8]LUE L, JIN Ci-hang, ZHOU Tao. Similarity index based on local paths for Link prediction of complex networks[J]. Physical Review E, 2009, 80(4): 1-9.

[9]Mangal D, Sett N, Singh S R, et al. Link prediction on evolving social network using spectral analysis[C]. Advanced Networks and Telecommunications Systems (ANTS), 2013 IEEE International Conference on. IEEE, 2013: 1-6.

[10]MASMOUDI M, EL B K, LOUKIL A, et al. Real-Time prediction of RTT based on Holt-Winters method for Internet-BasedTeleoperation[J]. International Review on Computers and Software(IRECOS), 2015, 10(1): 72-79.

(责任编辑：李孟良)

Research On Link Analysis and Prediction Based On Dynamic Network

YANG Lei1,2，LI Chen-long1,2

(1．Coll. of Comp. Info., Anhui Polytechnic University, Wuhu 241000，China;2．Key Laboratory of Computer Application Technology, Anhui Polytechnic University, Wuhu 241000, China)

Complex networks evolve rapidly over time by adding new nodes and new links, and it is difficult to get an accurate prediction by using the static characteristics of networks. By analyzing the dynamic characteristics of the networks, according to the tensor factorization theory, a new method of link prediction based on dynamic network is proposed, which is applied to the real complex dynamic network data for link analysis and prediction, The experiment demonstrates the advantages and effectiveness of this method, which achieves good prediction performance.

Link prediction; Dynamic network; Tensor factorization; Local path

2016-04-16

安徽省高等教育提升计划省级自然科学研究一般项目(TSKJ2015B20)；安徽工程大学计算机应用技术重点实验室开放基金项目(JSJKF201515)；安徽工程大学校青年基金项目(2009YQ040)。

杨磊(1982-)，男，安徽省临泉县人，硕士，讲师，主要从事数据挖掘研究。

TP391

A

1673-8772(2016)05-0062-05