光学元件挠性支撑结构广义建模及优化设计

曹玉岩，王志臣，周 超，范 磊，韩西达，张耀祖

(中国科学院 长春光学精密机械与物理研究所，吉林 长春 130033)



光学元件挠性支撑结构广义建模及优化设计

曹玉岩*，王志臣，周 超，范 磊，韩西达，张耀祖

(中国科学院 长春光学精密机械与物理研究所，吉林 长春 130033)

建立了挠性支撑结构的力学模型及优化设计模型，以使光学元件挠性支撑结构同时满足元件定位的刚度要求和温度适应性的柔度要求，同时给出了相应的建模方法。考虑挠性支撑结构是由圆周对称分布的挠性单元组成的，故将挠性单元简化为超静定梁结构，应用虚功原理推导了挠性单元的径向及切向刚度。然后，假设光学元件为刚性体，根据力平衡条件及变形协调条件，推导了挠性支撑结构的整体刚度，并引入修正因子补偿了刚体假设带来的误差。最后，以挠性支撑结构总变形能为目标函数，推导了同时考虑挠性支撑结构几何构形及参数的协同优化设计模型，通过引入了整型变量将结构整体刚度简化为整型变量和离散刚度的线性组合，从而使优化模型中不含有谐波函数项。基于数值仿真和实验对结构刚度模型进行了验证，结果显示：实验、仿真和理论计算结果一致。此外，以透镜支撑为例，验证了挠性支撑结构的优化设计方法，有限元分析结果表明，透镜面形精度较初始设计提高了23%。

光学元件；挠性支撑结构；广义模型；超静定；变形能；优化设计

1 引 言

挠性结构已广泛应用于多个领域，如光学设备[1]，陀螺仪[2]，传感器及驱动器[3]，微位移定位平台[4]。挠性结构得以广泛应用主要由于其具有以下优点：(1)具有很高的重复精度；(2)低摩擦性；(3)容易加工制造且成本相对较低。

光学元件的面形精度决定了光学系统性能，而光学元件的安装和定位结构又是保证面形精度的关键因素。在光学设备中，挠性结构主要用于光学元件的支撑与定位结构[5-7]。光学元件，尤其是大口径的元件，需要非常复杂的挠性支撑定位结构来保持元件的位置及面形精度[8-9]。这是因为挠性结构在某些自由度上具有一定的柔度，容许该自由度上有少量可控的相对位移，在其它方向上则具有较大刚度。在环境温度变化时，光学元件及其支撑组件将产生变形，热变形系数的不匹配将导致出现接触应力，接触应力将直接影响光学元件的面形，甚至造成破坏，而挠性结构的柔度可以有效地减小这部分接触应力[10-13]。

尽管挠性结构具有以上优点，但挠性支撑结构的建模非常复杂，尤其是多个挠性元件同时作用时。赵磊等[10]设计了光刻投影物镜中透镜的支撑结构，轴向采用的是多点挠性支撑结构，支撑中的弹性片简化为悬臂梁模型，但未深入分析弹性片数目对面形精度的影响。李宇轩等[14]针对空间遥感器大口径主反射镜提出了Cartwheel型双轴柔铰的三点挠性支撑结构，柔铰的参数采用无量纲设计方法确定。尽管通过此方法确定的参数可以满足设计要求，但无法确定此参数是否为最佳参数。曹乃亮等[15]提出将NiTi记忆合金丝复合于柔性件周边，借助预应变产生的拉应力来降低柔性件根部的应力集中问题，将柔性件切口等效为弯扭组合的梁结构，根据NiTi合金丝的本构方程设计了两种复合方案，采用有限元软件进行分析。

挠性支撑结构功能包括两个方面：(1)定位，即要求支撑结构具有一定的刚度，使得光学元件处在不同姿态时，能够保持其光轴位置不变；(2)协调变形，即当存在温度梯度时，支撑结构要有一定挠性来协调因热变形系数不匹配带来的变形偏差。挠性结构的这两方面功能是矛盾的，因为如果要保持位置不变，挠性件刚度应尽可能大，若为协调变形，则挠性件柔度应尽可能大。为平衡上述矛盾，需要根据挠性支撑结构的数学模型及使用要求，对各个参数进行优化，进而得到合理方案。为此，本文提出了一种挠性支撑结构的广义模型，该模型适合于多种类型的挠性支撑结构。在力学模型的基础上，提出了一种用于同时优化挠性支撑结构几何构形和参数的模型。模型中通过引入整型变量将挠性支撑结构整体刚度表达为整型变量与离散刚度的线性组合，从而简化模型优化的复杂程度。从数值仿真和实验角度对整体刚度模型进行验证，此外，以420 mm口径的透镜为例，进行了挠性支撑结构的优化设计，并应用有限元软件分析了优化设计前后透镜表面面形精度。

2 挠性支撑结构力学建模

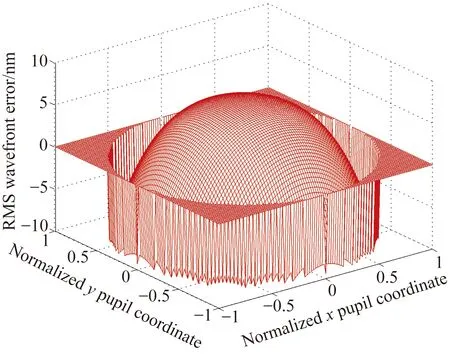
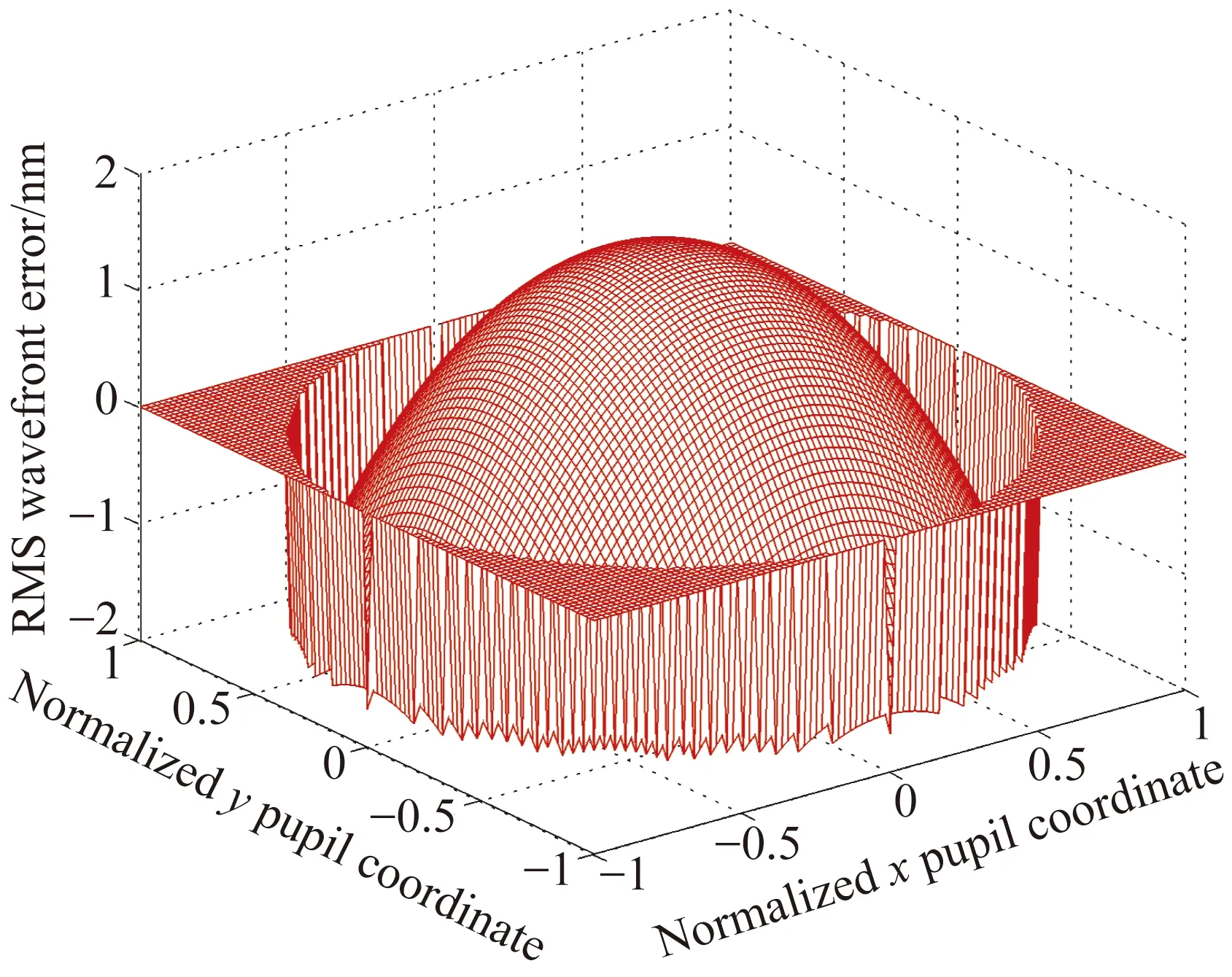
挠性支撑结构如图1所示。由图1可知，光学元件的边缘被粘接在多个相同的均匀分布的挠性单元上。相比传统刚性支撑结构，挠性支撑结构具有很多优点：(1)在受到冲击、振动及温度应力等影响后，光学元件的位置及共轴精度不会受到影响，因为挠性元件具有变形可恢复的特点；(2)当温度变化导致光学元件与其它结构变形不一致时，挠性结构可明显减小温度应力，因为挠性构件在光学元件热变形方向上具有较大柔度。以Φ110 mm透镜为例，温度变化为30 ℃时，传统刚性支撑与挠性支撑两种情况下，透镜上表面的变形如图2所示，其中刚性支撑情况下透镜下面形峰-谷值(PV)和均方根面形(RMS)分别为16.34 nm和4.12 nm，挠性支撑情况下透镜面形的PV和RMS分别为3.23 nm和0.82 nm。从图2中可以看出挠性支撑情况下透镜面形明显优于刚性支撑。此外，还可根据光学元件尺寸将该挠性支撑结构设计为不同的几何构形，以满足接触点处的最大应力要求，如图3所示。

尽管挠性支撑结构具有上述优点，但由于其存在挠性环节，使得光轴处于水平位置时会产生一定的偏移，且整个支撑组件的谐振频率要低于刚性支撑。为了合理设计该结构，需要研究光轴偏差、谐振频率与结构参数及几何构形的关系，进而使设计满足性能指标要求。

图1 挠性支撑结构概念

(a)刚性支撑

(b)挠性支撑

Fig.2 Deformation of top surface of lens under rigid and flexure mounting respectively

(a)三挠性单元

(b)四挠性单元

(c)五挠性单元

(d)六挠性单元

2.1 挠性单元刚度分析

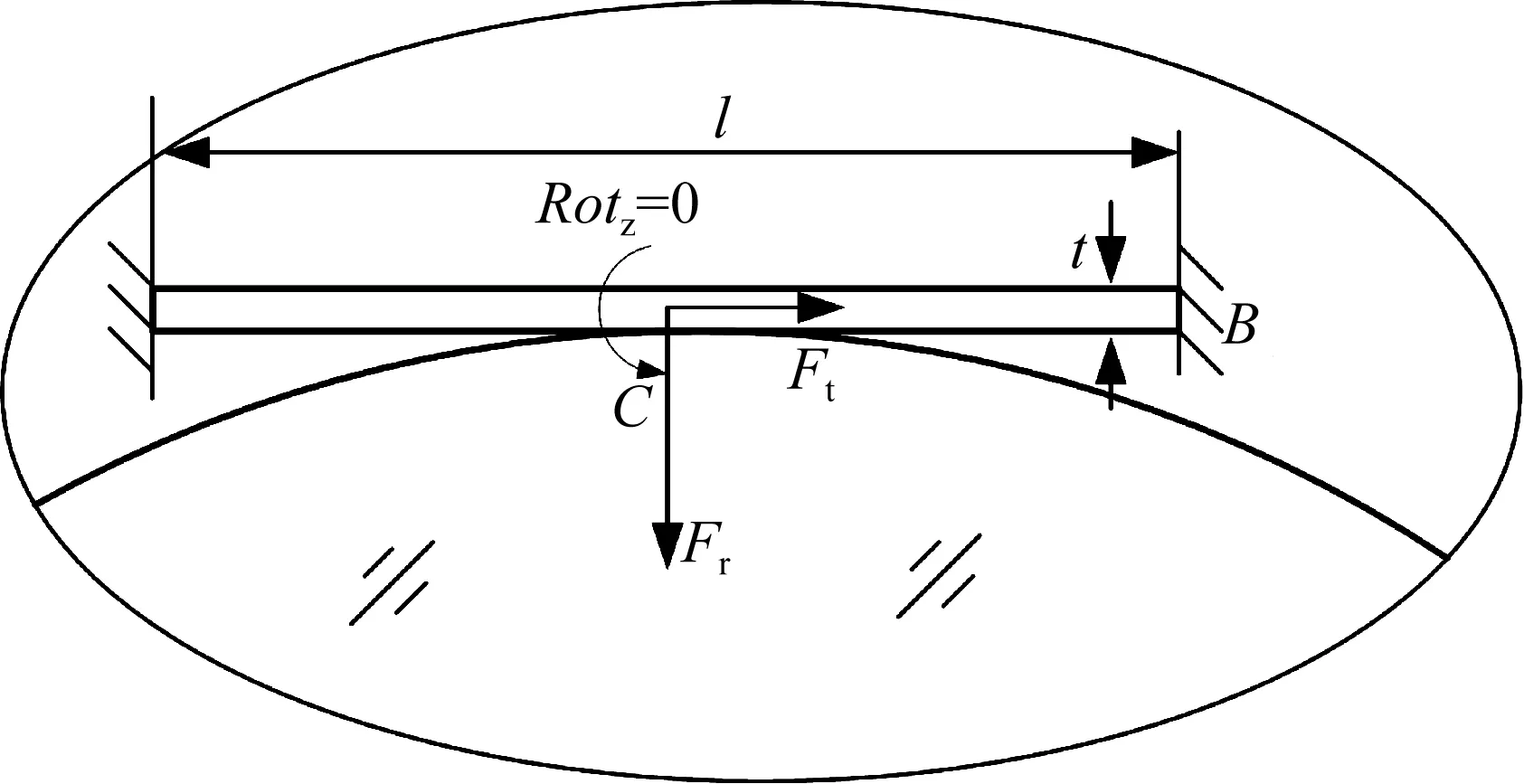
图1所示的挠性支撑结构中，关键部分为对称分布的挠性单元，如图4(a)所示。图4(b)为其等效模型。对于图1所示挠性支撑结构，Yolder[5]将其简化为弹簧结构，如图5所示，每个挠性单元具有径向和切向刚度。将挠性单元简化为两个方向上的弹簧虽是合理的，但在挠性单元与光学元件结合点处存在约束不足的问题，使得其等效刚度要小于实际模型刚度。为此，本文采用悬臂梁等效，如图4(b)所示，在结合点处增加了转动约束ROTz=0，使得结构成为超静定形式。挠性单元结构参数包括：有效长度l，厚度t，面内宽度b。

(a)挠性单元

(b)等效模型

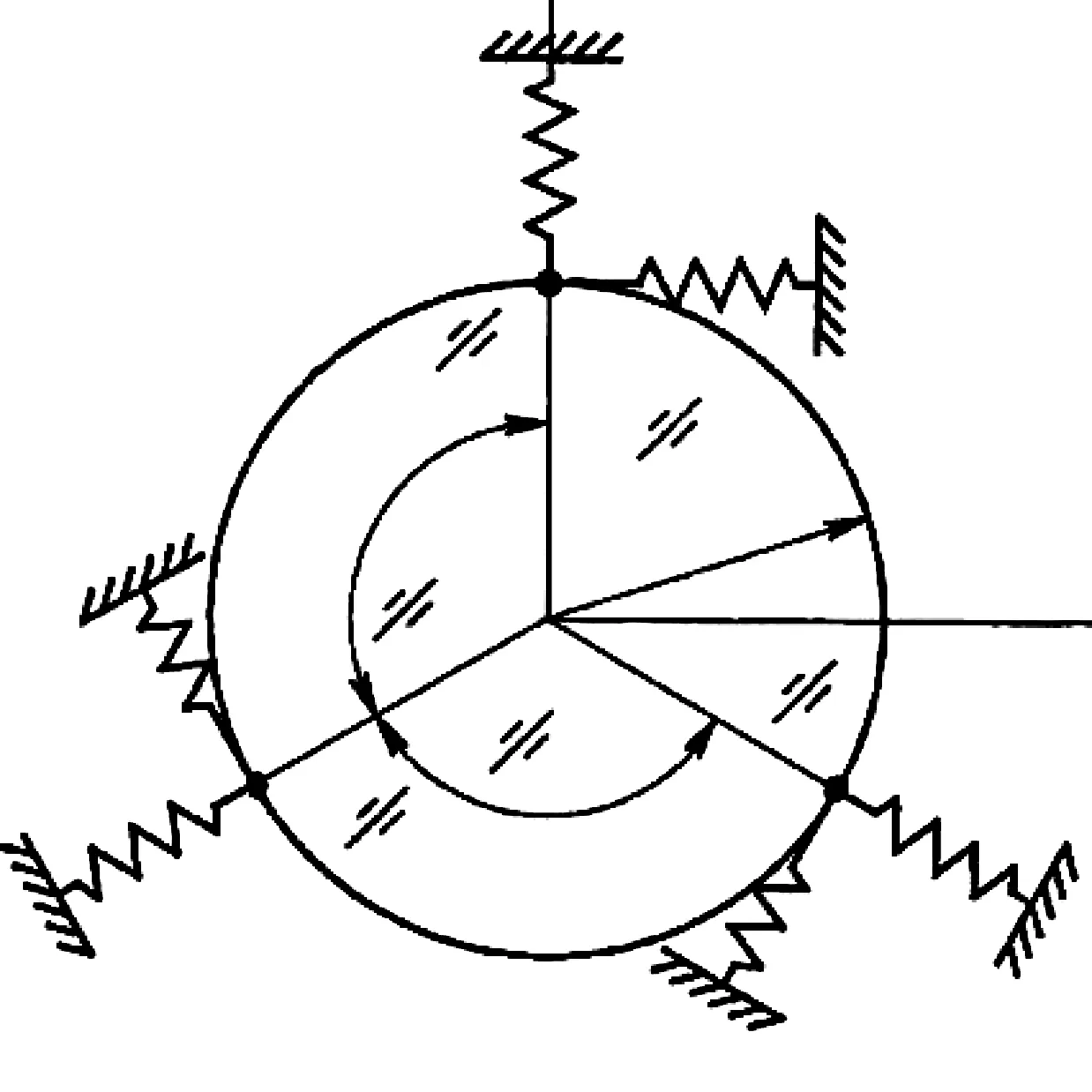
图5 挠性支撑的弹簧模型

解除图4(b)所示超静定梁上的连接点B和C的约束，其等效静定结构如图6所示，其中Xi(i=1，2，3，4)为未知广义力，Fr为径向力，Ft为切向力。

挠性单元的切向刚度Kt可以直接由下式得到：

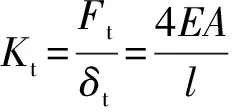
(1)

式中：δt为C点处的切向位移，E为弹性模量，A为截面面积。

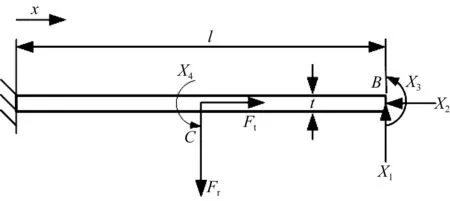
图6 超静定梁的等效静定结构

由图6可知，由径向力Fr和未知力Xi引起的悬臂梁截面上的弯矩为：

(2)

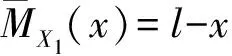
(3)

(4)

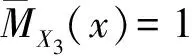
(5)

(6)

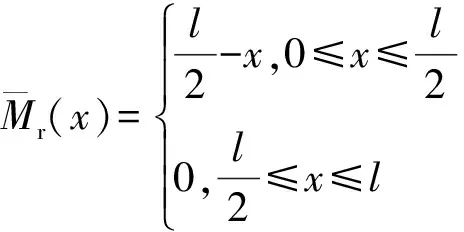
(7)

根据虚功原理，在C点处由Fr和Xi引起的位移分别为：

(8)

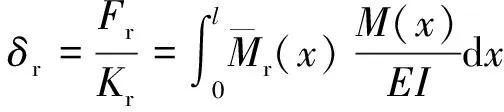
(9)

由B点和C点处位移边界条件，结合式(8)和(9)可得：

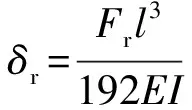
(10)

(11)

挠性单元的最大弯曲应力为：

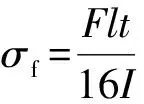
(12)

2.2 挠性支撑结构整体刚度分析

按挠性单元的悬臂梁等效模型，将图3所示的挠性支撑结构等效为如图7所示的模型，若其安装时存在夹角α，其受力分析和位移分析结果如图8所示。模型中考虑了几何构形的因素，即挠性单元数量对刚度的影响。图8中Fi表示连接点Pi处挠性件受到的外力，可将其分解为径向力和切向力Fir和Fit，Fiy为Fi的竖向分力，δir和δit分别表示连接点Pi处的径向位移和切向位移，δiy表示竖向位移，δix表示横向位移，n为挠性单元的数目i=1，2，…，n。

图7 挠性支撑结构等效模型

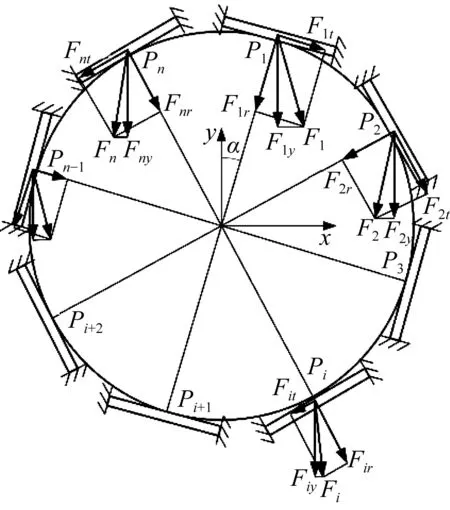
(a)力分析

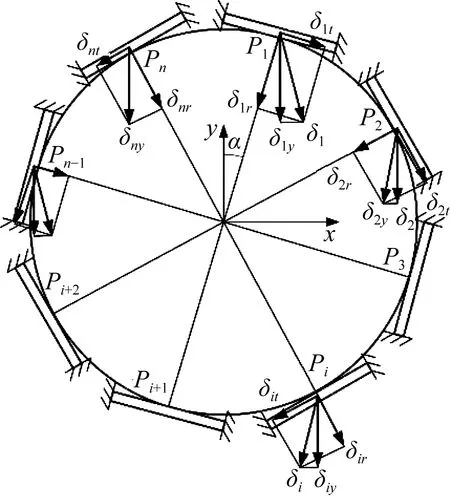
(b)位移分析

根据几何关系，竖向分力Fiy(i=1，2，…，n)可表示为：

(13)

根据竖向力平衡关系，即：

(14)

式中G为光学元件的重力。

竖向位移δiy可表示为：

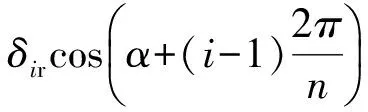
(15)

由于重力方向竖直向下，挠性支撑结构连接点Pi处将仅有竖向位移，即：

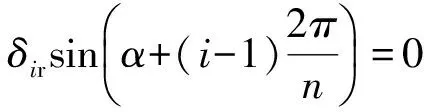
(16)

根据式(16)知，δir和δit的关系可表示为：

(17)

与光学元件相比，挠性支撑整体具有一定的柔度，因此在推导光学元件整体刚度时，可假设光学元件为一刚性体，则连接点Pi处的位移δiy均相等，即：

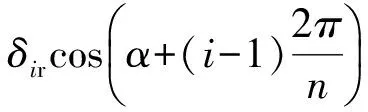
(18)

由式(16)和(17)得：

(19)

由式(1)知，每个连接点Pi的径向位移和切向位移同样满足胡克定律，即：

Fir=Krδir，Fit=Ktδit.

(20)

由式(14)，(18)～(20)得：

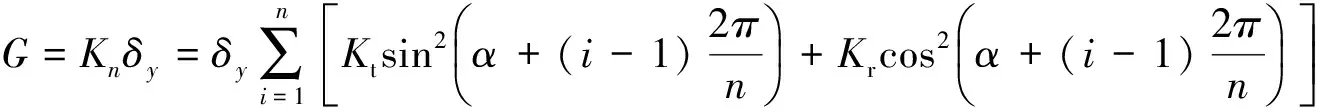
(21)

挠性支撑结构的整体刚度为：

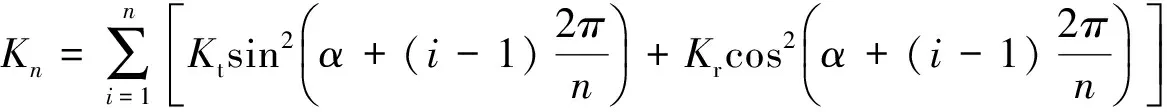
(22)

将式(1)和(11)代入式(22)得：

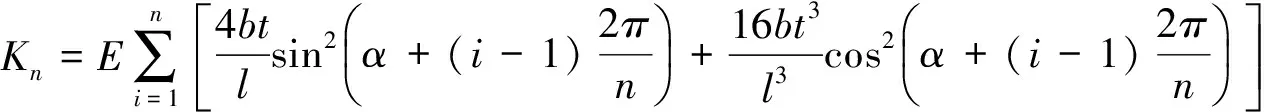
(23)

从式(23)可看出，该挠性支撑结构的整体刚度是弹性模量E，厚度t，宽度b，长度l，挠性单元数目n及安装角度α的函数，即：

Kn=F(E，b，t，l，n，α).

(24)

这里要说明，尽管刚度表达式(23)是按竖向位移推导而来，但其具有一般性，即其它方向的刚度可以通过改变α值得到。

此外，若考虑到光学元件或其他构件自身的变形，则挠性支撑结构的整体刚度小于由式(24)表示的刚度。为此，在整体刚度模型，即式(24)中引入了修正因子λ，即：

Kn=λ·F(E，b，t，l，n，α)，

(25)

式中：λ大小由与挠性元件相连构件的刚度决定，完全刚性时λ=1。

作为特例，b=8，t=0.5，l=20，λ=1，材料为65 Mn，整体刚度Kn随安装角度α及挠性单元数目n的变化曲线如图9所示。

从图9中可以看出，随安装角度α变化挠性支撑的整体刚度保持不变。而保持参数不变情况下，随着连接点数目增多，整体刚度增大。

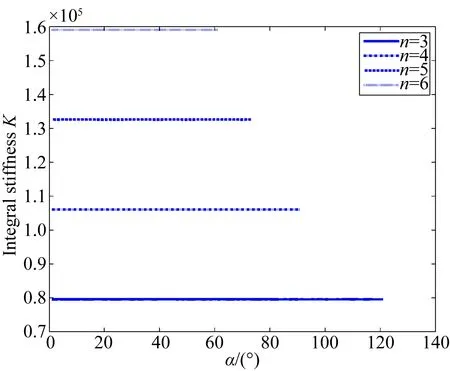
图9 整体刚度与安装角度及连接点数目关系

Fig.9 Relationship between integral stiffness with mounting angle and the number of connecting points

3 考虑几何参数及构形的挠性支撑结构优化设计

对于一个光学元件，如透镜或反射镜，设计挠性支撑结构，涉及选择合适的材料，确定其最佳构形及几何参数，以满足光学指标要求。

以往的研究主要是先假定一种初始构形，然后优化几何参数，若得到的几何参数不符合工程应用实际，则改变其构形，重复上述过程。然而，这样的优化并不能保证几何构形及参数的最佳匹配。为此，本文提出了一种几何构形及参数协同优化的设计方法。通常，挠性支撑结构材料选择热胀系数较小的铟钢，其设计一般需要满足以下条件：光轴水平放置时，光轴的偏移量要尽可能小，每个挠性单元的最大应力要满足其强度条件，每个连接点处的应力要满足光学材料的强度条件，此外，面形精度要尽可能高。

根据式(23)和上述设计要求知，该挠性支撑结构的一般模型可表达为：

minΦ(E,b,t,l,n)

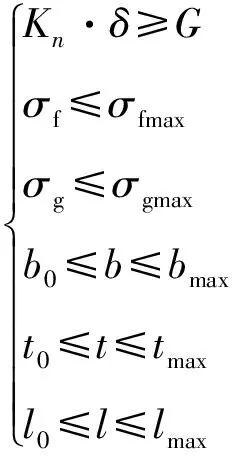
(26)

式中：Φ为目标函数，可根据需要选择不同指标作为目标函数，σf和σfmax分别为挠性单元的应力和其材料的最大许用应力，σg和σgmax分别为连接点处应力及光学材料的许用应力，b0，t0，l0，bmax，tmax，lmax分别为b，t，l的最小值与最大值。

由于挠性单元数目n无法加工为任意数目，且非整数的连接点数也无意义，因此n仅能取整数值。由式(23)表达的刚度模型是非常复杂的谐波函数，此类函数的优化非常困难。仔细观察发现，若n取为整数值，则刚度表达式(23)也变为与n相对应的离散值，为此，在优化模型中引入0-1型整数变量xi(i=n0，n1，…，nmax)来简化刚度表示式(23)。

首先引入径向刚度系数Krn和切向刚度系数Ktn，将式(23)表达为：

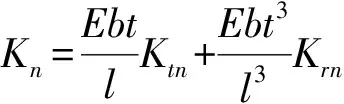
(27)

式中：Krn，Ktn为由n确定的常数。

然后利用设计变量xi(i=n0，n1，…，nmax)，将挠性支撑结构整体刚度表示为：

xn1Kn1+…+xnmaxKnmax，

(28)

式中：设计变量xi取值为0或1，有且仅有一个xi取值为1，其余为0。

利用式(28)，优化模型(26)可重新表达为：

minΦ(E,b,t,l,xi)

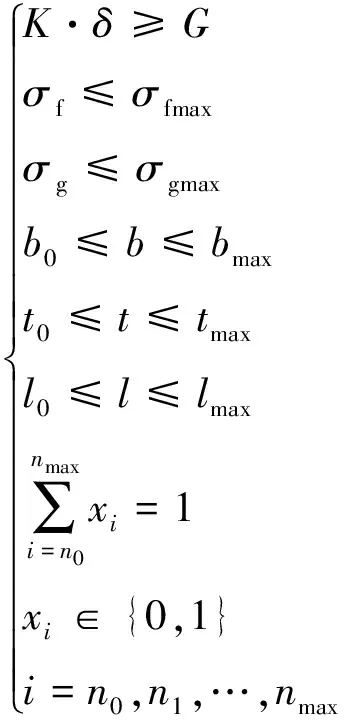
(29)

式(29)中不含有谐波函数，简化了模型的复杂性，使求解过程变得简单。本文采用Lingo软件整数和实数混合规划程序完成上述模型的求解计算。

4 数值模拟与实验测试

为了验证提出的挠性支撑结构的力学模型及设计挠性支撑结构几何构形及参数的协同优化算法，进行了如下数值仿真及实验。

4.1 挠性支撑结构整体刚度仿真与实验

以3个挠性单元情况为例，对挠性支撑结构进行仿真和实验测试。挠性支撑结构试验件和有限元模型如图10所示，结构参数如表1所示。这里，挠性支撑与实际中用于支撑光学元件的结构有一些差别，主要为了方便测试其刚度。测试内容包括：(1)在结构一侧施加拉力，拉力大小由力传感器监视，采用直线光栅尺测量输出位移，根据位移随力的变化曲线得到结构整体刚度，图11所示x轴方向；(2)转动挠性支撑结构，使其具有一定的安装角度，测试其它方向上的刚度，验证结构刚度与安装角度的关系，图11所示y向和Ⅰ及Ⅱ方向。实验测试装置如图12所示，其中测力传感器精度为0.1 N，光栅尺的测量精度为0.1 μm。

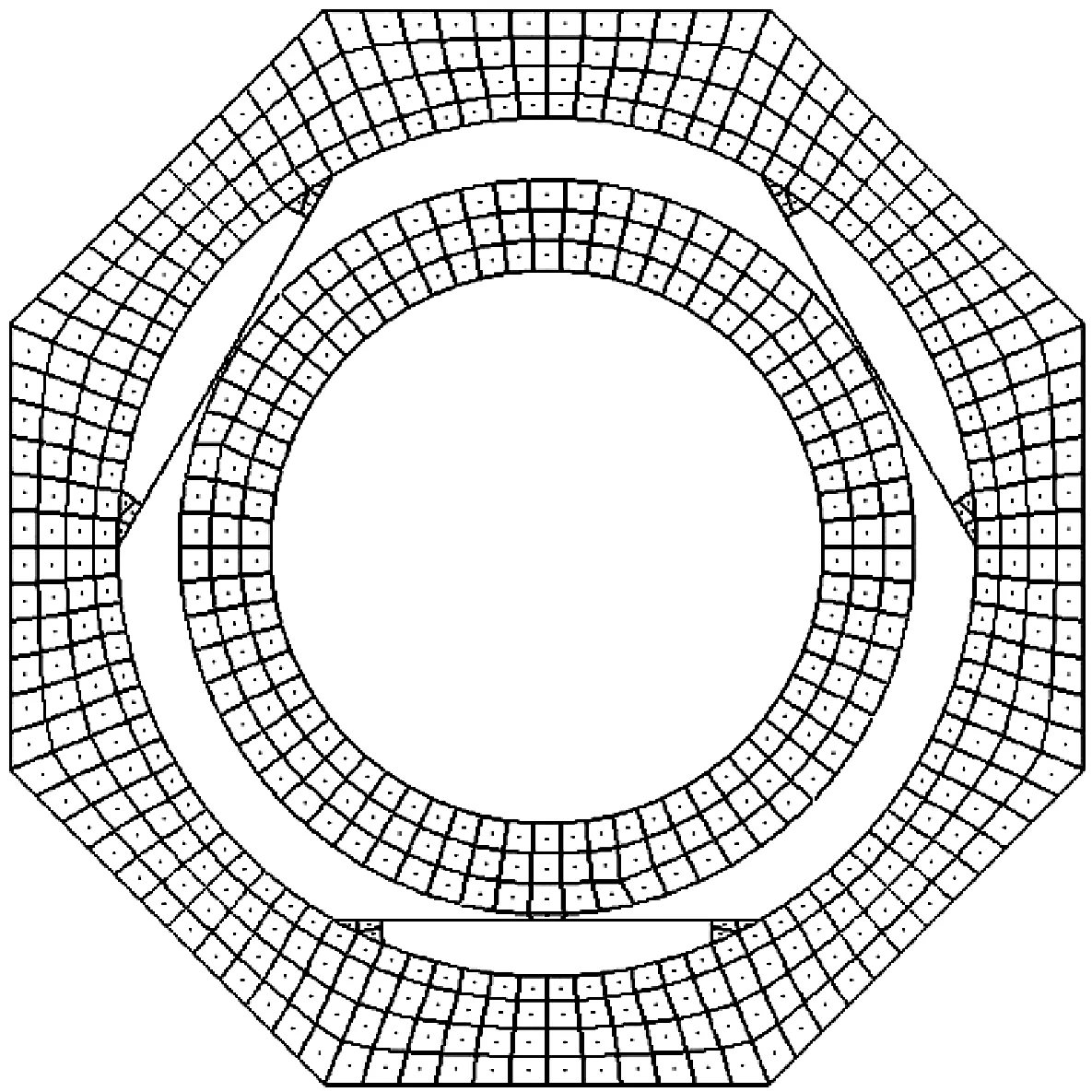
图10 挠性支撑结构件及其有限元模型

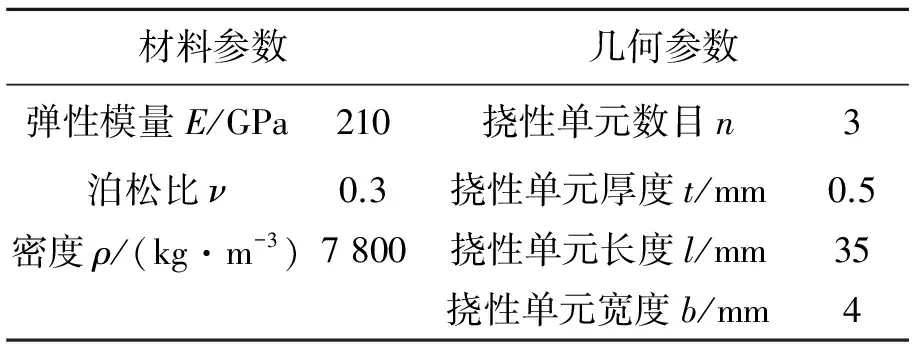
材料参数几何参数弹性模量E/GPa210挠性单元数目n3泊松比ν0．3挠性单元厚度t/mm0．5密度ρ/(kg·m-3)7800挠性单元长度l/mm35挠性单元宽度b/mm4

图11 刚度测试方向

图12 实验测试装置

分别对挠性结构件x轴，y轴和Ⅰ方向施加0～400 N的作用力(Ⅱ方向与Ⅰ方向反对称)，间隔为20 N，并在有限元模型及本文推导的理论模型上施加同样的力，测量和计算得到的数据如表2～4所示。

表2 试验件x向刚度测试数据

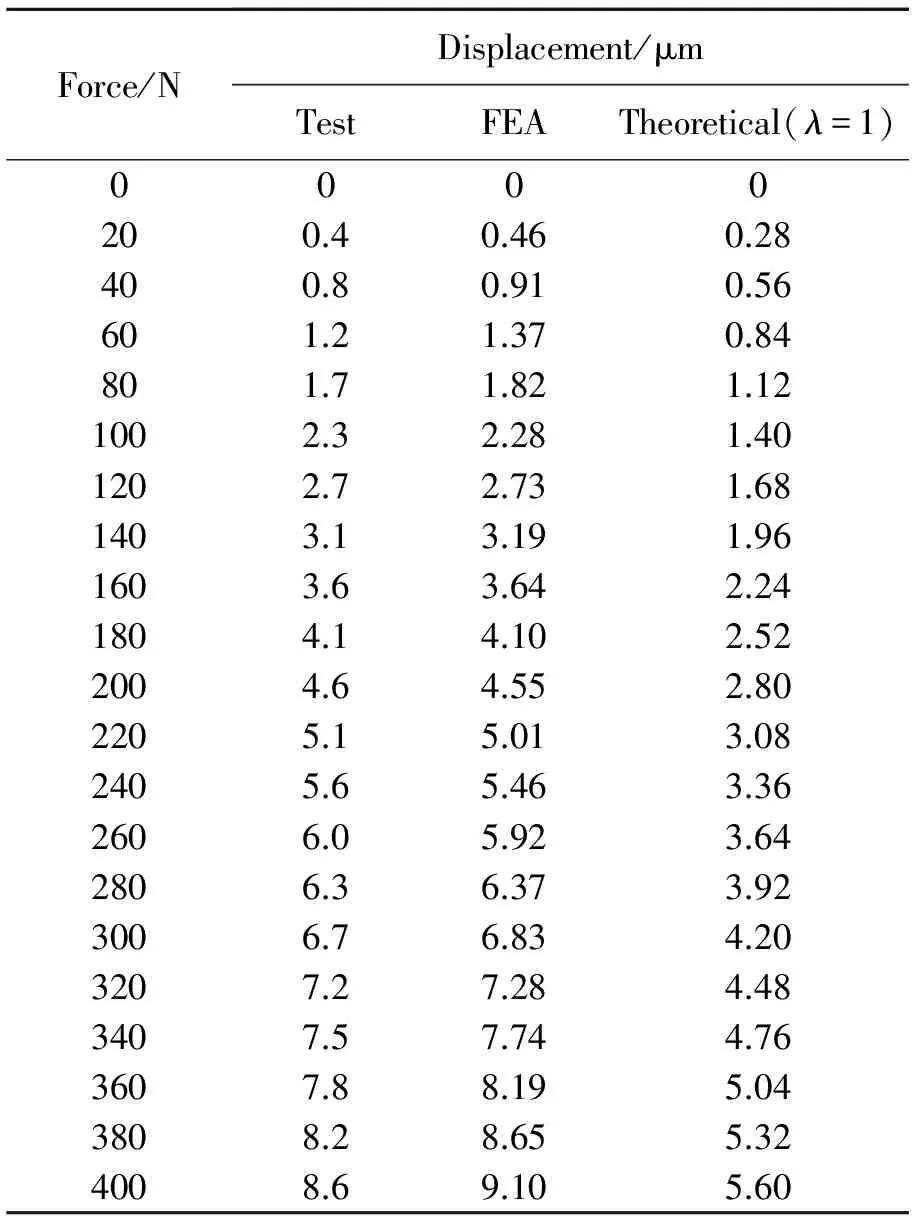
表3 试验件y向刚度测试数据

表4 试验件Ⅰ向刚度测试数据

应用最小二乘法分别对3个方向上刚度测试得到的离散位移数据进行线性拟合，得到的拟合结果、数值仿真及理论计算结果如图13～15所示。

从图13～15可以看出，3个方向上位移测试数据与有限元仿真数据吻合的非常好。然而，从图13～15中还可以看出，由整体刚度模型(23)(即修正因子λ=1)计算得到的结果明显小于实测及有限元仿真结果，其原因在于推导式(23)时，假设除挠性单元外其余部分为刚体，而试验件的外框架并非理想刚体，因此实际挠性支撑结构的整体刚度低于理论计算结果。通过比较发现，当修正因子λ=0.65时，3个方向上的理论结果与实验及仿真结果完全吻合。

此外，从3个方向的测试数据可看出，3个方向上的位移数据基本一致，证明此挠性件在各个方向上的刚度是一致的，与本文推导的理论模型结论一致。

图13 x方向数据结果

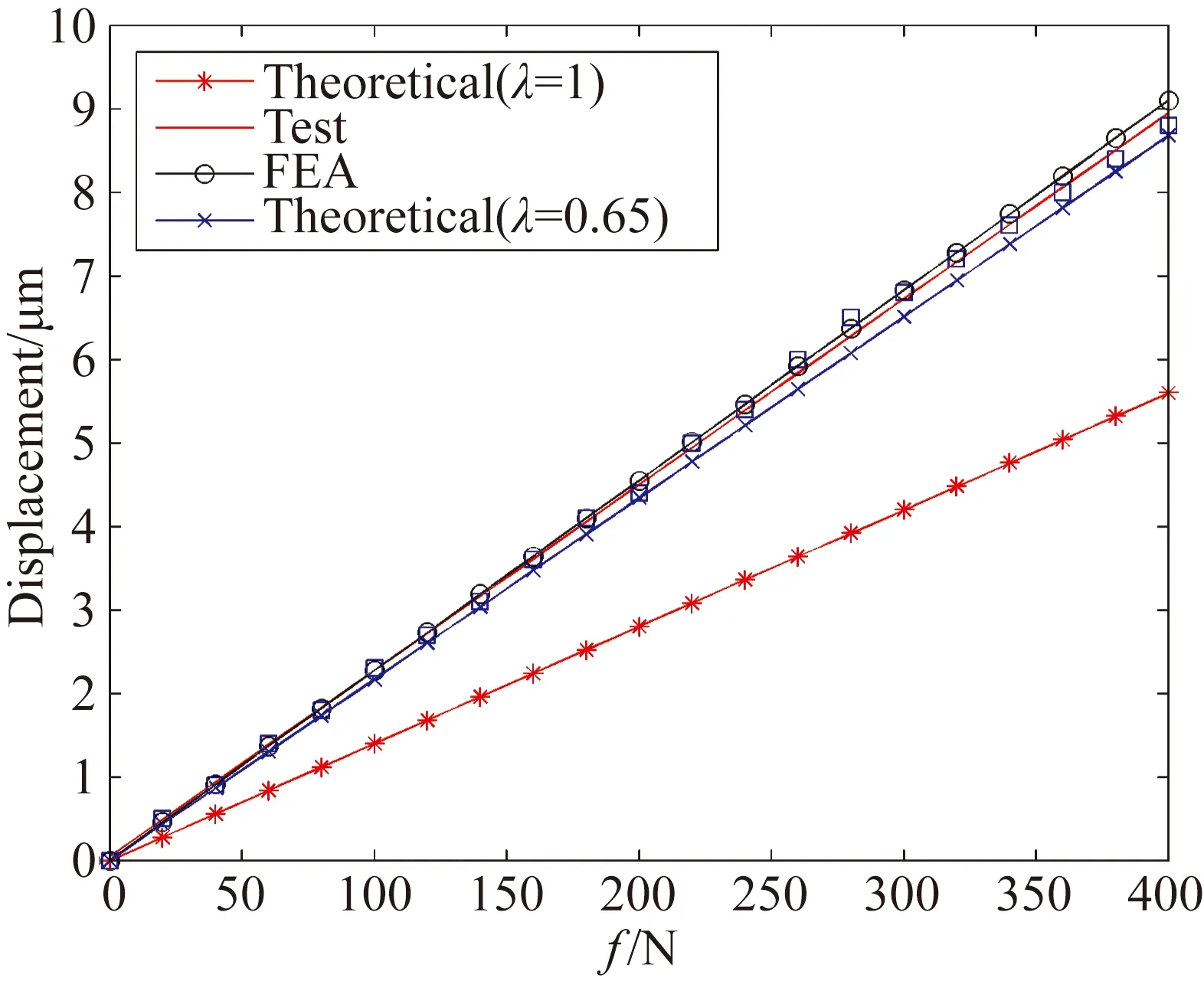
图14 y方向数据结果

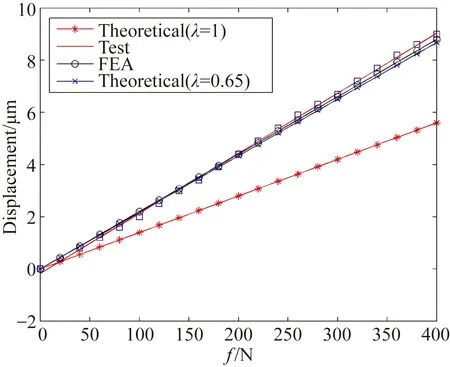
图15 Ⅰ方向数据结果

4.2 挠性支撑结构的优化设计

以透镜支撑为例，透镜的结构参数如表5所示，设计该透镜的挠性支撑结构，使其面形精度达到最优，且在不同仰角位置光轴晃动量小于0.5 μm。由于透镜面形精度很难用解析式表达，通常是采用有限元方法计算其变形，然后通过曲面拟合得到面形精度值[16-17]，这使得优化模型时无法直接利用面形精度作为目标函数或约束条件，而只能采用间接的方法。已有研究表明，面形精度随透镜与挠性单元作用力的增大而变差，但并未考虑挠性单元数目的影响。为此，本文以挠性支撑结构的总变形能作为目标函数，这样能够同时考虑挠性单元与透镜的相互作用力及挠性单元数目对面形精度的影响，材料选取铟钢4J32，参数如表6所示，将光轴位移作为约束条件，则优化模型可表达为：

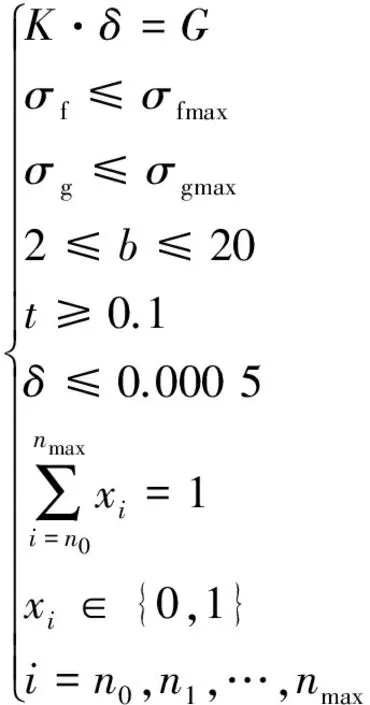
(30)

式中：δT是温差为ΔT是透镜的径向变形，挠性件几何参数约束由加工能力决定，这里为简化模型取l=35 mm。

表5 透镜参数

表6 铟钢材料参数

以3个挠性连接点情况为初始设计，首先调整挠性支撑结构参数，即厚度t和宽度b使得光轴水平时，光轴偏移满足要求，并以此为初始设计参数。应用本文提出的优化模型即式(30)对透镜挠性支撑结构进行优化，确定最佳的挠性单元数目及结构参数。

针对初始和最优情况下的结构参数，分别建立相应的有限元模型，并分析在环境温差为50 ℃时，透镜上表面的变形，其中有限元分析在PATRAN/NASTRAN软件中实现。然后，分别对得到的变形数据进行拟合，除去刚体位移项，计算透镜表面的面形误差RMS值。由于理想的温差环境及在此环境下检测透镜面形需要的实验条件非常复杂，在此仅对其进行了数值仿真分析。

初始设计参数与最佳设计参数如表7所示，其中面形误差RMS值为透镜上表面面形，初始和最优情况下透镜的变形如图16(彩图见期刊电子版)所示。

表7 初始及最佳参数

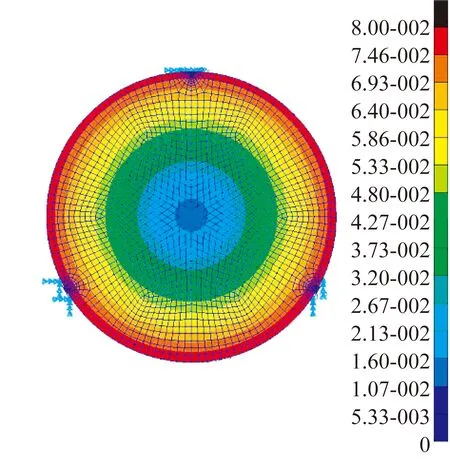
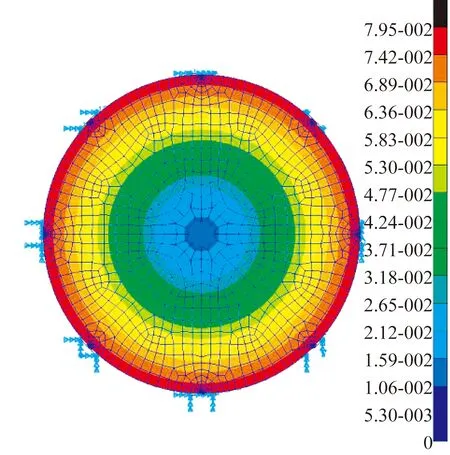
图16 初始情况和最佳情况下透镜变形云图

模型的优化目标函数为环境存在温差ΔT时挠性件的总变形能，从表7可以看出，最优情况下的变形能及面形误差均小于初始3个连接点情况，表明挠性件变形能可以反映透镜的面形误差，以此为目标函数来简化优化模型是合理的。此外，通过有限元分析得到的透镜面形误差RMS值可以看出，通过优化透镜的面形精度提高了23%。

5 结 论

本文针对光学元件挠性支撑结构设计中刚度和柔度要求之间的矛盾，建立了光学元件挠性支撑结构的力学模型及优化设计模型。根据挠性支撑结构的特性，将各个挠性单元简化为超静定的梁，并推导了挠性单元的径向及切向刚度。假设光学元件为刚性体，根据力平衡条件及变形协调条件，推导了挠性支撑结构的整体刚度，并引入了修正因子补偿由刚体假设带来的误差。以挠性结构总变形能为目标函数，推导了同时考虑挠性支撑结构几何构形及参数的协同优化设计模型，模型中通过引入了整型变形将结构整体刚度简化为整型变形和离散刚度的线性组合，从而使优化模型中不含有谐波函数项。从数值仿真和实验角度对整体刚度模型进行验证，实验结果与仿真及理论计算结果吻合的非常好。此外，透镜挠性支撑结构优化设计结果表明，通过优化，透镜面形精度较初始设计提高了23%。

[1] SCHWERTZ K， BURGE J.FieldGuidetoOptomechanicalDesignandAnalysis[M]. Washington USA： SPIE Press， 2012.

[2] PAROS J M， WEISBORD L. How to design flexure hinge [J].MachineDesign， 1965， 37(1)：151-157.

[3] CAI K H， TIAN Y L， WANG F J，etal.. Development of a piezo-driven 3-DOF stage with T-shape flexible hinge mechanism [J].RoboticsandComputer-IntegratedManufacturing， 2016， 37(2)：125-138.

[4] XU Q. Design， testing and precision control of a novel long-stroke flexure micropositioning system [J].MechanismandMachineTheory， 2013， 70：209-224.

[5] YOLDER P R.Opto-MechanicalSystemsDesign[M]. Third ed. Washington： CRC Press， 2006.

[6] YOLDER P R.MountingOpticsinOpticalInstruments[M]. Second ed，Washington：SPIE Press，2008.

[7] FATA R， KRADINOV V， FABRICANT D. Flexure mounts for high-performance astronomical lenses [J].Proc.SPIE， 2006，6269，doi：101117/12.672634.

[8] 范磊， 张景旭， 吴小霞， 等. 大口径轻量化主镜边缘侧向支撑的优化设计[J]. 光学 精密工程，2012，20(10)：2207-2213. FAN L， ZHANG J X， WU X X，etal.. Optimum design of edge lateral support for large aperture lightweight primary mirror [J].Opt.PrecisionEng.， 2012， 20(10)： 2207-2213.(in Chinese)

[9] 陈夫林， 张景旭， 吴小霞，等. 620 mm薄镜面的主动支撑结构及面形校正[J]. 光学 精密工程，2011，19(5)：1022-1029. CHEN F L， ZHANG J X， WU X X，etal.. Supporting structure of 620 mm thin primary mirror and its active surface correction [J].Opt.PrecisionEng.， 2011， 19(5)： 1022-1029.(in Chinese)

[10] 赵磊，巩岩. 光刻物镜中透镜高精度支撑结构的设计及分析[J]. 光学学报，2012，32(9)：0922001-0922009. ZHAO L， GONG Y. Design and analysis for the high-precision lens support structure of ojective lens for lithography [J].ActaOpticaSinica， 2012， 32(9)： 0922001-0922009.(in Chinese)

[11] 倪明阳，巩岩. 光刻投影物镜光学元件运动学支撑结构的设计与分析[J]. 中国光学，2012，5(5)：476-484. NI M Y， GONG Y. Design and analysis of kinematic lens positioning structure in lithographic projection objective [J].ChineseOptics， 2012， 5(5)： 476-484.(in Chinese)

[12] 马磊，曹佃生，刘承志. 大口径透镜多点柔性支撑结构设计与分析[J]. 光电工程，2015，42(5)：88-94. MA L， CAO D SH， LIU CH ZH. Design and analysis on multi-points flexible supporting structure of large-aperture lens [J].Opto-ElectronicEngineering， 2015， 42(5)： 88-94.(in Chinese)

[13] 赵磊， 彭海峰， 于新峰，等. 具有整体径向挠性的光学元件多点均匀支撑结构[J]. 光电工程，2015，42(10)：43-48. ZHAO L， PENG H F， YU X F，etal.. Lens support structure of multi point equal supporting with wholly radical freedom [J].Opto-ElectronicEngineering， 2015， 42(10)： 43-48.(in Chinese)

[14] 李宇轩， 陈雪， 张雷，等. 大口径空间反射镜Cartwheel型柔性铰链支撑设计[J]. 光学学报，2014，34(6)：0622003-0622009. LI Y X， CHEN X， ZHANG L，etal.. Design of Cartwheel flexural support for a large aperture space mirror [J].ActaOpticaSinica， 2014， 34(6)： 0622003-0622009.(in Chinese)

[15] 曹乃亮， 徐宏， 辛宏伟， 等. 基于NiTi合金丝的反射镜柔性支撑结构的应力补偿[J]. 光学 精密工程，2012，20(10)：2161-2169. CAO N L， XU H， XIN H W，etal.. Stress compensation of flexible supporting structures for mirrors using NiTi shape memory alloy [J].Opt.PrecisionEng.， 2012， 20(10)： 2161-2169.(in Chinese)

[16] 曹玉岩， 王志， 周超，等. 压电智能反射面静态形状控制与作动器位置优化[J]. 航空学报，2015，36(2)：527-537. CAO Y Y， WANG ZH， ZHOU CH，etal.. Static shape control of piezoelectric smart reflector and optimization of actuators placement [J].ActaAeronauticaetAstronauticaSinica， 2015， 36(2)： 527-537.(in Chinese)

[17] 王志， 曹玉岩， 周超，等. 柔性压电智能反射面的静态形状控制[J]. 光学 精密工程，2014，22(10)：2715-2724. WANG ZH， CAO Y Y， ZHOU CH，etal.. Static shape control of flexible piezoelectric smart reflectors [J].Opt.PrecisionEng.， 2014， 22(10)： 2715-2724.(in Chinese)

曹玉岩(1986-)，男，吉林大安人，助理研究员，2009年、2012年于西安电子科技大学分别获学士、硕士学位，主要从事结构有限元理论、结构振动控制技术研究。E-mail：yuyan_cao@126.com

王志臣(1980-)，男，黑龙江大兴安岭人，副研究员，主要从事望远镜光机结构设计研究。E-mail：zcwang911@163.com

(本栏目编辑：马 健)

(版权所有 未经许可 不得转载)

General modeling and optimal design of flexure supporting structure for optical components

CAO Yu-yan*， WANG Zhi-chen， ZHOU Chao， FAN Lei， HAN Xi-da， ZHANG Yao-zu

(Changchun Institute of Optics， Fine Mechanics and Physics，ChineseAcademyofSciences，Changchun130033，China)

A mechanical and a parameter optimization model for flexure support structure of optical components were proposed to allow the flexure structure meet simultaneously the requirements of the stiffness for optical component position and the compliance for temperature adaptability。Meanwhile， the corresponding modeling method was investigated. As this flexure structure was consisted of several identical flexure parts， it was simplified into an indeterminate beam structure， and the radical stiffness and tangential stiffness were derived using the virtual work principle. Then， by assuming optical components for the rigid body， the whole stiffness of the flexure support structure was derived based on the force equilibrium and its compatible deformation， and the correction factor was introduced to compensate the error caused by the rigid assumption. Finally， the total strain energy of the flexure structure was taken as the objective function， and the collaborative optimization model was derived considering the geometrical pattern and parameters simultaneously. By introducing the integral variables， the whole stiffness of the structure was simplified into a linear combination of the integral variable and discrete stiffness， and the harmonic terms were eliminated. The whole stiffness model was verified by the simulation and experiment， and the experiment results are highly in agreement with the simulation results. A lens mounting was taken for an example， the optimization method of the flexure mounting structure was verified. The finite element simulation results show that the surface precision of the lens has been improved by 23%.

optical component； flexure mounting structure； general model； indetermination； strain energy； optimization design

2015-12-23；

2016-02-04.

国家自然科学基金资助项目(No.11403023)

1004-924X(2016)11-2792-12

TH703；TP273

A

10.3788/OPE.20162411.2792

*Correspondingauthor，E-mail：yuyan_cao@126.com