双层规则随机网络上伴随意识衰败的模型分析∗

安江波，赵爱民

(山西大学数学科学学院，山西太原030006)

双层规则随机网络上伴随意识衰败的模型分析∗

安江波，赵爱民∗

(山西大学数学科学学院，山西太原030006)

考虑双层网络的SAIS模型，其中警觉者由于意识衰败可能成为易感者。用逼近Markov过程的方法推导基于个体的伴随意识衰败的信息传播SAIS模型。在规则随机网络下，分析了模型的动力学行为.证明了伴随意识衰败，信息传播的SAIS模型的第二阈值消失。

复杂网络;意识衰败;SAIS模型;阈值

近年来，研究人类对传染病的反应是一个非常重要的话题[1]，并且引起了大量的关注[2-7]。这个话题关注的不仅是怎样模拟疾病存在时人类的反应，而且模拟这些反应如何影响疾病本身的传播。一般情况，对于疾病的传播，人类的反应可以分为三类:1)改变个体的状态。例如，免疫直接导致个体从易感状态到恢复状态而没有经历染病状态。2)改变传染病模型的参数。例如，个体可能选择戴面具从而降低了染病率[7]。3)改变接触网络的拓扑结构。例如，个体可能减少或者改变与潜在染病者的接触[2]。Polett等人发展了基于人群(population-based)的模型，易感者面对传染病可能有两种行为:一种是不受传染病影响保持以前的生活方式；另一种是对传染病有警觉，做好防护措施。例如减少与外界的接触[8]。Funk等人证明了对疾病有意识的个体数量的增加能减少疾病爆发的概率[4]。

这些基于人群的模型适合于均匀混合的个体，进而关于异质网络的结论被提出[9]。Pastor等人在无标度网络上研究疾病的传播[10]。基于个体(individual-based)的传染病模型被提出，接触网络用通用图表示，每一个节点表示一个个体，边表示接触。已经证明，复杂网络上的SIS模型的疾病传染强度的阈值等于接触图谱半径的倒数[11-12]。

Sahneh在文[13]中考虑了信息对疾病传播的影响，将易感者分为易感者和警觉者(有意识的易感者)。易感者与染病者接触时，可能被传染成为染病者；也可能未被疾病传染，但可能获得一些与疾病有关的信息而成为警觉者。警觉者与染病者接触可能被传染，成为染病者；染病者恢复后都成为易感者。Sahneh假设信息与疾病的传播路径相同，即信息只能通过接触而传播，从而建立了单层网络上的SAIS模型，得出疾病传染强度的两个阈值，并分析了疾病在阈值之间的传播动力学性态。得出信息的传播导致了疾病传染强度第二阈值的产生。

疾病信息的获得有两个基本来源。一个来源是通过实际接触网络，另一个是通过社交网络信息传播(例如微信，QQ)。在文[13]的基础上Sahneh在文[14]中考虑疾病信息的传播，进而建立了重叠网络上的疾病与信息传播的SAIS-ID动力学模型，并给出疾病传染强度的第二阈值的表达式。

David Juher等人在文[15]同样考虑单层网络的SAIS模型，在此基础上引入意识衰败，随着时间警觉者会成为易感者，作者考虑的网络是规则随机网络，也就是网络所有节点有相同的度，而每个节点的邻居是随机选择。同样证明单层网络的SAIS模型存在第二阈值，伴随意识衰败的SAIS模型会导致第二阈值消失。

本文结合文[14][15]，考虑伴随意识衰败的SAIS-ID模型，首先给定一个重叠网络，一层为接触层，疾病在接触层中传播；另一层为信息层，信息通过非接触的方式(如:电子邮件，社交网络等)或与染病者日常接触的方式(如:生活，工作等)进

1 模型的建立

1.1 网络结构

1.2 建立模型

考虑网络中总节点数为N，每个节点可以为三种状态的一种:S“易感者”，I“染病者”，A“警觉者”(有意识的易感者)。 令 X t()＝表示t时刻网络节点的状态，若节点i在t时刻是染病者，记xit()＝e1，若为警觉者xit()＝e2，若为易感者xit()＝e3。

伴随意识衰败的SAIS-ID模型中，疾病与意识在双层网络中的传播规则为:在接触层，易感者与染病者接触时，可能被传染成为染病者的概率为β0；也可能未被疾病传染，但可能成为警觉者的概率为λ0；警觉者与染病者接触并被传染成染病者的概率为β0a(0＜β0a＜β0)；染病者恢复为易感者的概率为δ；警觉者成为易感者的概率为δa；在信息层，由于信息传播，易感者与染病者在虚拟网络中接触并成为警觉者的概率为μ0。

记mi≜[pi，ai，si]T，其中pi，ai，si分别表示节点i为染病者，警觉者，易感者的概率，即。于是，对于充分小的Δt，有:

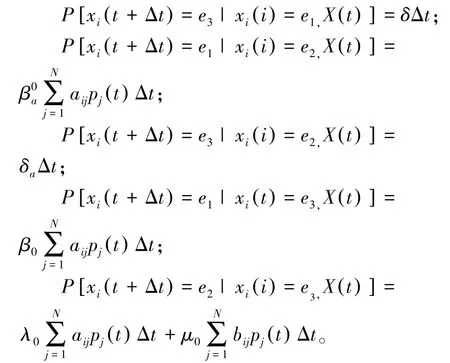
从而，由全概率公式得:

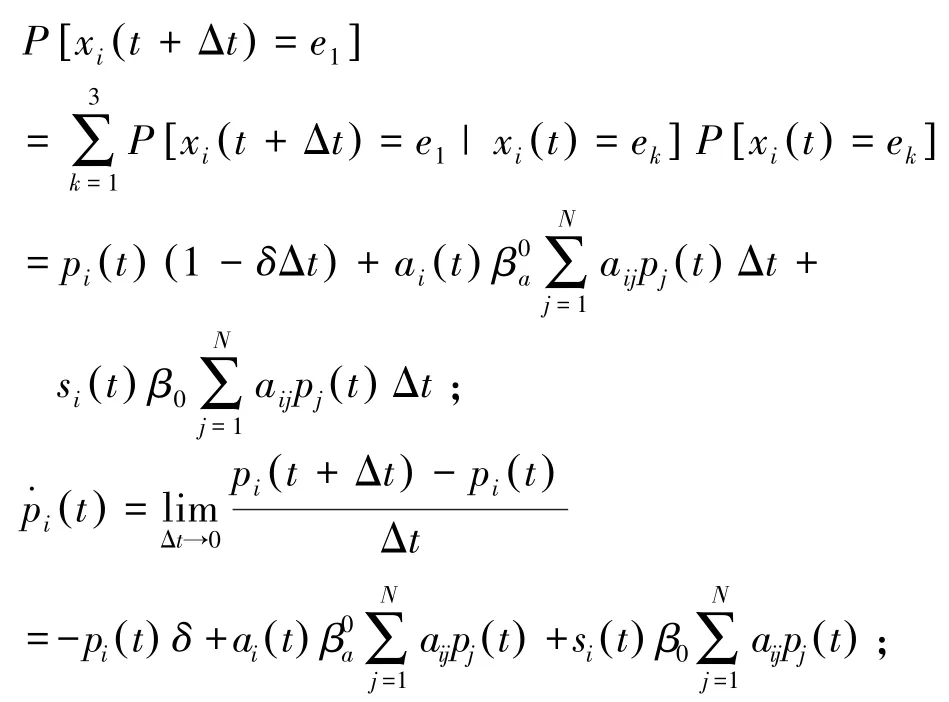
同理可得:

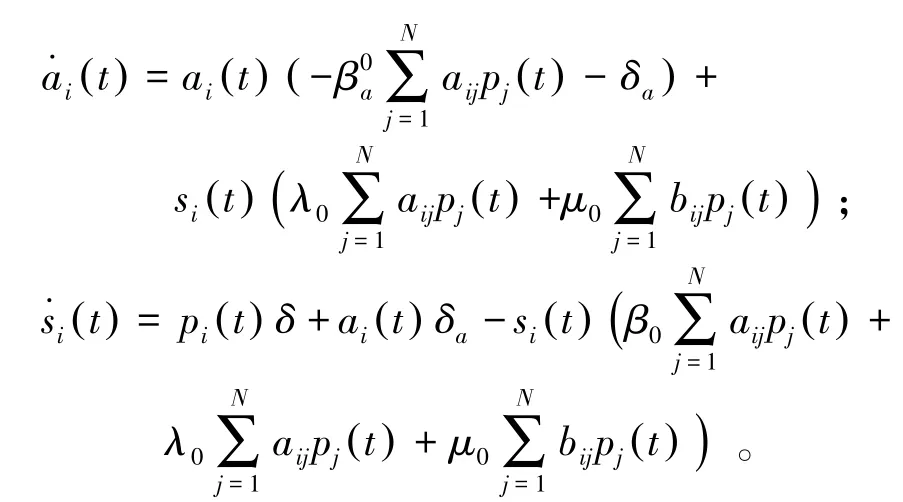
因此，mi随时间变化的微分方程如下:

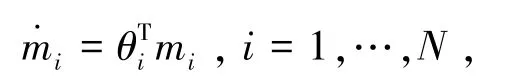
其中

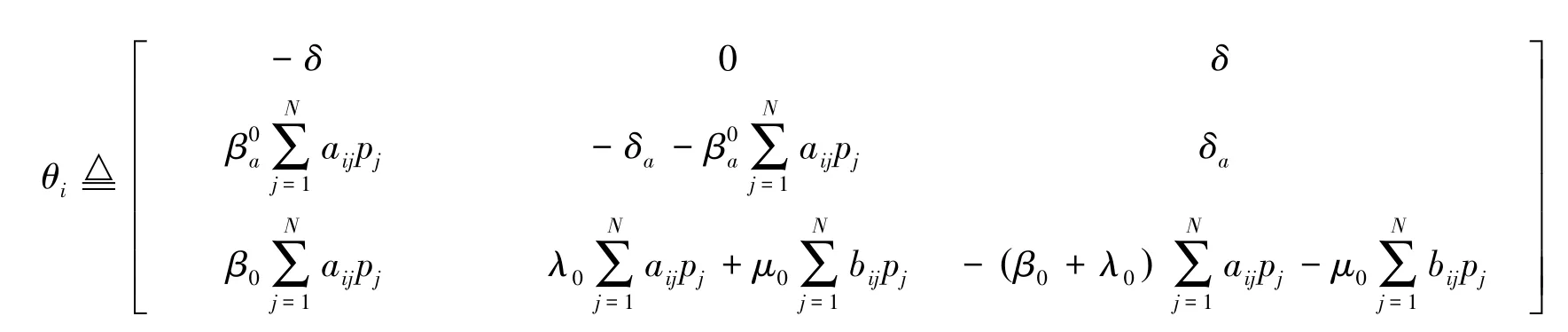
是无穷小量转移矩阵。因为pi+ai+si＝1，因此模型为:

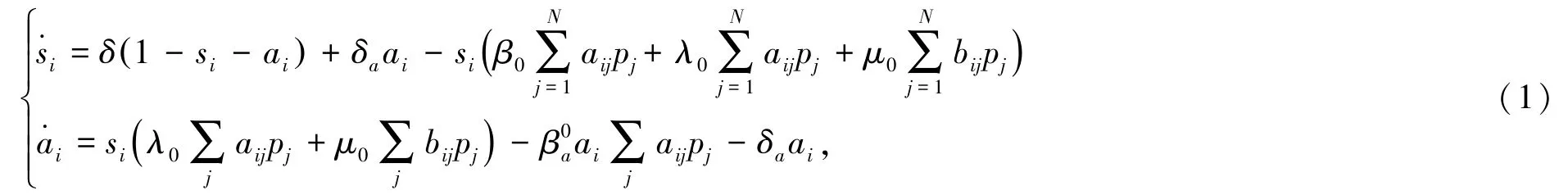
2 模型分析

下面在规则随机网络上进行分析。此时节点随机连接，所有节点的度都相同。记k1为接触层每个节点的度，k2为信息传播层每个节点的度。

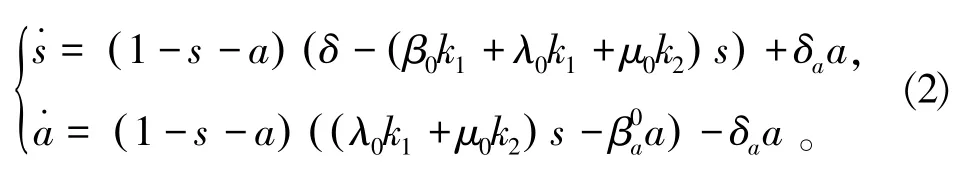
(0，1)且s0+a0≤1，考虑微分方程:易知(2)存在唯一解满足初始条件。由解的存在唯一性定理可知，2，…，N的唯一解。在规则随机网络上，模型(1)就转化为模型(2)，为了方便起见，记β＝k1β0，βa＝。则模型(2)可写成:就是模型

(1)满足初始条件

2.1 没有意识衰败情形

首先我们考虑模型没有意识衰败情形，即(3)中δa＝0的情形，此时模型为；

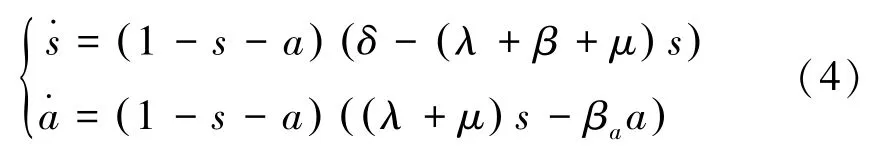
显然，直线段a+s＝1上的点都是(4)的平衡点，而且 都 是 无 病 平 衡 点。记 E ＝，L ＝。易知E是系统的正不变集。由问题的实际意义，只需在正不变集E上考虑系统(4)即可。

直接计算可知系统(4)还有一个平衡点

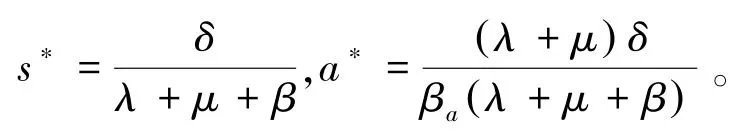
从而系统(4)有地方病平衡点的充要条件为: s∗+a∗＜1。

注意到，当u＝0时模型(3)就退化为文[15]中的模型，利用文[15]的结论，可得:

定理1 假设βa，β，λ，μ，δ＞0且βa＜β，系统(4)解的全局行为为以下情况的一种:

(b)若βa＜δ＜β，

(ii)μ＜μ∗时，存在地方病平衡点s∗，(a∗)，地方病平衡点局部渐近稳定。

(c)若δ＜βa，s∗，(a∗)为全局渐近稳定。注 与文[15]相比，考虑了信息可以通过信息网络层传播，更符合实际意义。增加信息层警觉意识有利于降低地方病平衡点出现的可能，降低疾病爆发的最终规模。

当β≤δ或δ＜βa时，警觉意识不起作用。因为当β≤δ时，恢复率比易感者的染病率大，疾病不会爆发，与警觉意识无关；当δ＜βa时，恢复率比警觉者的染病率小，疾病一定爆发；当βa＜δ＜β时，此时警觉意识起作用，如果易感者以较大的概率成为警觉者，从而降低染病的风险。

2.2 意识衰败的情形

下面考虑模型(3)中δa≠0的情形。

易得(1，0)为系统(3)的无病平衡点。集合E，L同2.1。易知L是系统(3)的正不变集，当t→∞，轨迹每一点 a，s( )∈L趋于无病平衡点，E是系统(3)的正不变集。

同样利用文[15]的结论，可得:

定理2 假设βa，β，λ，μ，δ＞0，βa＜β，若δ≥β，则系统(3)在正不变集E区域没有异于无病平衡点的平衡点，无病平衡点全局渐近稳定。

定理3 假设βa，β，λ，μ，δ，δa＞0，βa＜β，若δ＜β，则系统(3)在正不变集E内部存在唯一一个平衡点，且全局渐近稳定。

注:当δ＜β时，与模型(4)相比，模型(3)地方病平衡点全局渐近稳定，此时疾病第二阈值消失。

3 模拟

本文主要是伴随意识衰败SAIS-ID模型，我们模拟β＞δ时系统(4)的相图(图1)与系统(3)的相图(图2)比较。取δa＝0.05。

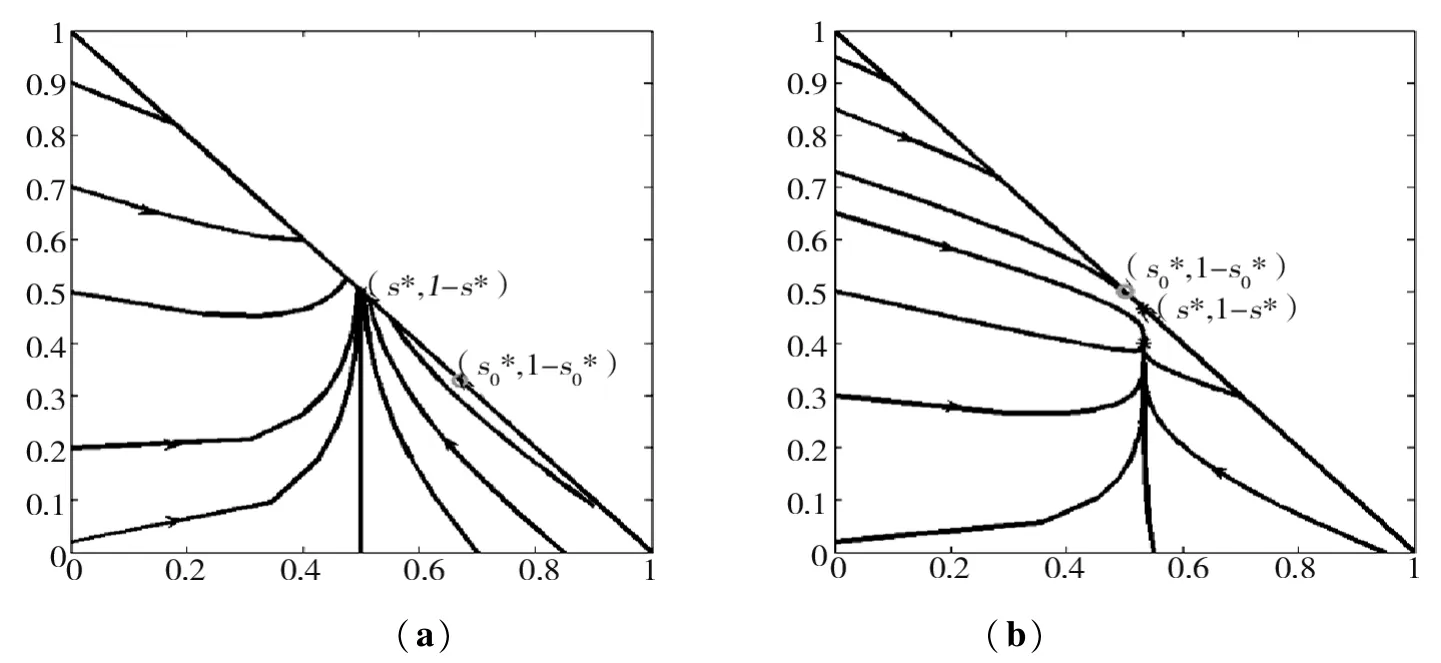
图1 图中(a)(b)参数分别为

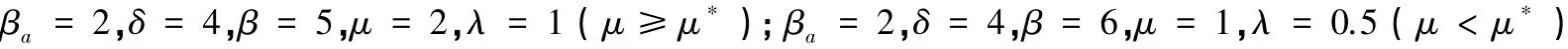
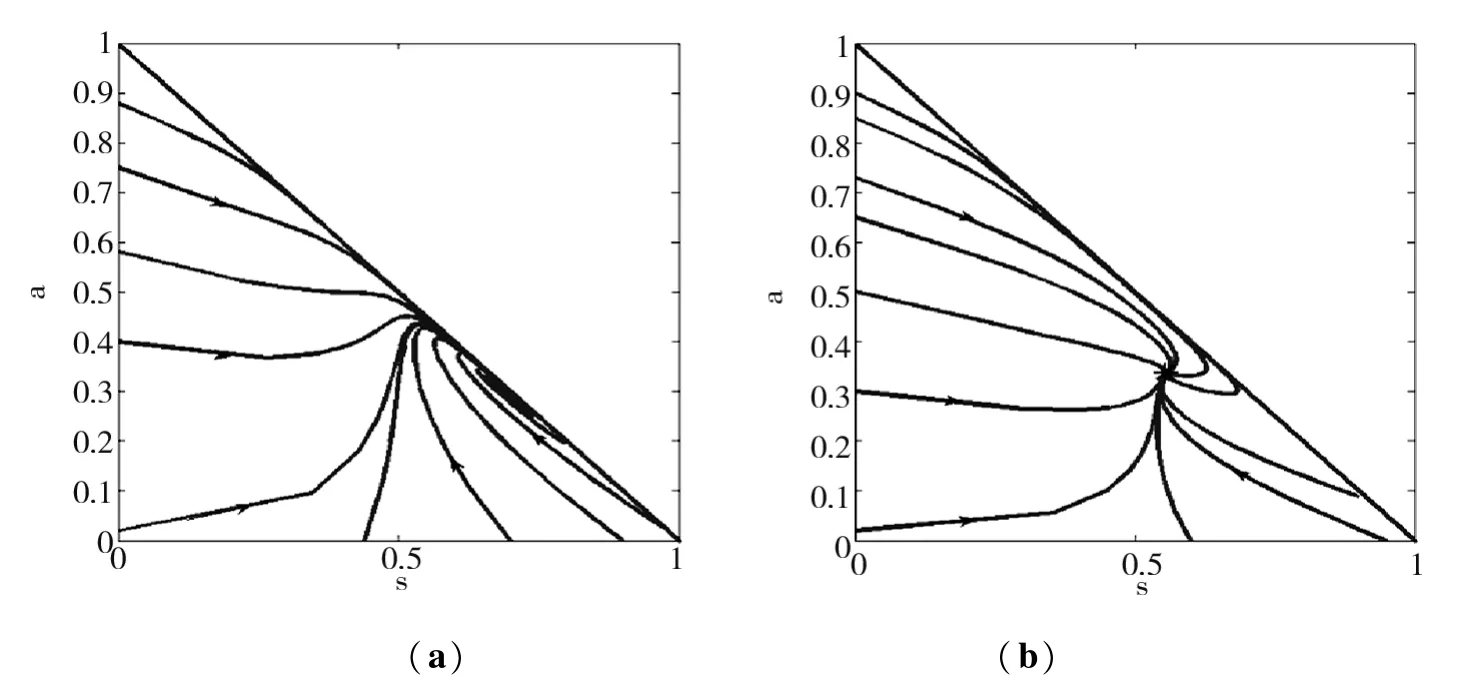
图2 图中(a)，(b)参数分别为

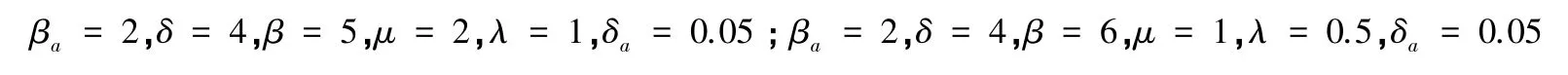
从图2(a)中可以看出，地方病平衡点接近a+ s＝1的边界，也就是对应于疾病爆发；(b)图中所有的轨迹趋于E内的地方病平衡点。

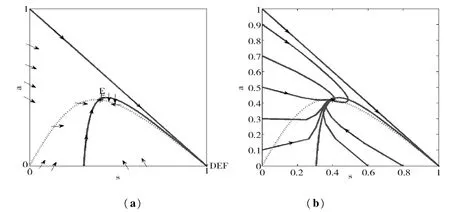
图3 图(a)系统(3)的向量场β＞δ，图(b)系统(3)的相图

从图3中可以看出当β＞δ时，系统(3)只有唯一一个地方病平衡点，且是全局渐近稳定。

在图4中(o)βa＝2，δ＝4，β＝6，μ＝1，λ＝2，(+)βa＝2，δ＝4，β＝6，μ＝1，λ＝0.5。这些初值相同，s(0)＝0.9，a(0)＝0。(△)与(+)参数相同，初值不同，s(0)＝0.05，a(0)＝0.85。从左图可以看出+与△不能趋于相同的值，因为(s∗，a∗)不是全局稳定，右图看出由于小的意识衰败，+与△趋于相同的值，因为(s∗，a∗)是全局渐近稳定，但需要更长的时间达到稳定状态。

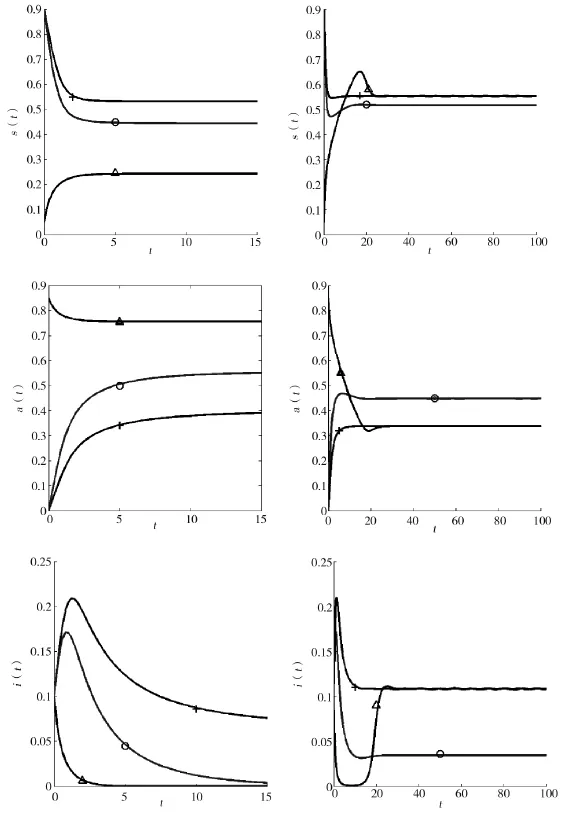
图4 典型的时间演化过程的解系统(4)(左图)和系统(3)(右图)，δa＝0.05

[1]N.Ferguson.Capturing human behaviour[J].Nature，2007，446 (7137):733-733.

[2]Funk S，SalathéM，Jansen V A A.Modelling the influence of human behaviour on the spread of infectious diseases:a review[J]. Journal of the Royal Society Interface，2010，7(50):1247-1256.

[3]S.Kitchovitch，P.Lio.Risk perception and disease spread onsocialnetworks[J].Procedia Computer Science，2010，1(1):2339-2348.

[4]Funk S，Gilad E，Watkins C，et al.The spread of awareness and its impact on epidemic outbreaks[J].Proceedings of the National Academy of Sciences，2009，106(16):6872-6877.

[5]S.Funk，E.Gilad，V.Jansen.Endemic disease，awareness，andlocal behavioural response[J].Journal of Theoretical Biology，2010，264(2):501-509.

[6]I.Kiss，J.Cassell，M.Recker，et al.The impact of information transmission on epidemic outbreaks[J].Mathematical biosciences，2010，225(1):1-10.

[7]S.Tracht，S.Del Valle，J.Hyman，etal.Mathematicalmodeling of the effectiveness of facemasks in reducing the spreadof novel influenza a(h1n1)[J].PloSONE，2010，5(2):e9018.

[8]PolettiP.Human behavior in epidemicmodelling[D].Petersburg: University of Trento，2010.

[9]Y.Moreno，R.Pastor-Satorras，A.Vespignani.Epidemic outbreaks in complex heterogeneous networks[J].The European PhysicalJournal B-Condensed Matter and Complex Systems，2002，26(4):521-529.

[10]Pastor-Satorras R，Vespignani A.Epidemic dynamics and endemic states in complex networks[J].Physical Review E，2001，63(6):066117.

[11]Wang Y，Chakrabarti D，Wang C，et al.Epidemic spreading in real networks:An eigenvalue viewpoint[C]//Reliable Distributed Systems，2003.Proceedings.22nd International Symposium on.IEEE，2003:25-34.

[12]P.Van Mieghem，J.Omic，R.Kooij.Virus spread in networks [J].Networking，IEEE/ACM Transactions on，2009，17(1): 1-14.

[13]Sahneh，F.D.，Scoglio，C.Optimal information dissemination in epidemic network[C]//Decision and Control(CDC)，2012 IEEE 51st Annual Conference.New York:IEEE，2012.

[14]Sahneh，F.D.，Chowdhury，F.N.，Brase，G.，et al.Individualbasedinformation dissemination in multilayer epidemic modelin [J].Math.Model.2014，9(2):136-152.

[15]David Juher，Istvan Z.Kiss.Analysis of an epidemic model with awareness decay on regular random network[J].Journal of Theoretical Biology，2015，365:457-468.

(责任编辑:曾 晶)

Analysis of A SAIS Epidem ic M odel w ith Awareness Decay on Regular Random Overlay Network

AN Jiangbo，ZHAO Aimin∗

(School of Mathematical Sciences，Shanxi University，Taiyuan 030006，China)

A SAISmodel on overlay network was considered where an alert individualmightgo to the susceptible state with awareness delay.Individual-based information disseminationmodel with awareness delay was derived through themethod of approximation Markov process.Under the regular random network，the dynamic behavior of themodel was analyzed.Furthermore，the disappearance of the second epidemic threshold was proved with awareness delay on information dissemination SAISmodel.

complex network；awareness decay；SAISmodel；threshold

O175

A

1000-5269(2016)04-0019-06

10.15958/j.cnki.gdxbzrb.2016.04.04

2016-05-10

国家自然科学基金资助项目(11471197)；山西省自然科学基金资助项目(2014011005-1)

安江波(1989-)，女，在读硕士，研究方向:生物动力系统，Email:918030392＠qq.com.

∗通讯作者:赵爱民.Email:zhaoam＠sxu.edu.cn.行传播。两层网络具有相同的节点，但不同层的连边具有不同的含义。用逼近Markov过程的方法推导基于个体的伴随意识衰败的SAIS-ID模型。分析模型时考虑的是规则随机网络，同样证明了伴随意识衰败，信息传播的SAIS模型的第二阈值消失。