Koranyi单位球面上的一类特殊算子∗
2016-12-19王振华张为元李艳艳
王振华,张为元,李艳艳
(咸阳师范学院数学与信息科学学院,陕西咸阳712000)
Koranyi单位球面上的一类特殊算子∗
王振华,张为元∗,李艳艳
(咸阳师范学院数学与信息科学学院,陕西咸阳712000)
针对海森堡型群无界域上的一类Dirichlet方程的求解问题,构造了一个线性算子,并研究了它的紧性以及特征值和特征向量。
嵌入定理;紧算子;特征值和特征向量
在无穷维Banach空间中,紧算子是一类特殊的线性算子,其性质类似于有限维空间中的矩阵,因此关于线性方程解的结果可以推广到含紧算子的线性偏微分方程中去。紧算子在偏微分方程理论的研究中起着核心的作用。
1995年,Birindelli[1]在Rn中的有界域M上定义了一个算子是的解,并证明了T1是一个紧算子;2001年,Birindelli[2]在海森堡(Heisenberg)群上推广De Giorgi猜想[3]的过程中证明了如下结果:令Ω′⊂S1H⊂Hn,如果算子 T2∶L2(Ω′)→ L2(Ω′),u(φ)=T2f是 Dirichlet方程的解,那么T2是一个紧算子,并且T2具有正的特征值和正的特征向量。
本文基于Birindelli[2]的成果,将上述结果推广到了海森堡型群上。下面海森堡型群的定义是Kaplan在文献[4]中引入的。
若对任意ξ2∈V2,|ξ2|=1,映射J(ξ2)∶V1→V1是正交的,则称G是一个Heisenberg型群。G上的度量函数为

G上的群运算法则为

G中的Koranyi单位闭球为

1 由极坐标导出算子T
首先我们引入海森堡型群上的极坐标概念(文献[5][6])。
ρ(δλ(x,y))=λρ(x,y),θ∈∂BG(e,1)。设光滑函数u∶∂BG(e,1)→R,在∂BG(e,1)上定义微分算子:

并且


其中ai=Xi(ρ),bj=ρYj(ρ),^Ri,^Sj是Xi,Yj在S1G上的切分量,且满足

由(1),(3)计算得到

,引进下列算子

因为在S1G上存在特征点[7],^Ri是Xi在S1G上的投射,所以在S1G上具有形如ξ0=(0,…,1,…,0)的特征点,对任意的f,g∈L2(Ω,dθ),我们定义f,g的内积为
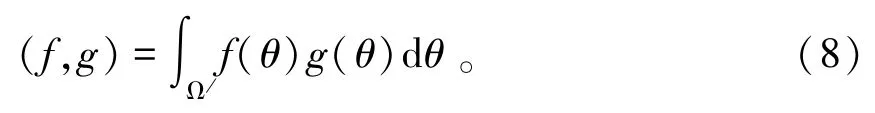
设B0是C∞0(Ω)关于‖u‖B0的闭包,‖u‖B0可表示为

定义算子
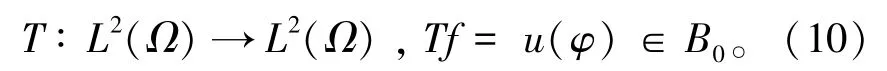
这里的u是下列边值问题

的解,T的紧性条件是求解上述边值问题的必要条件。下面我们将证明T是一个紧算子。
2 T的紧性
在这一节,我们证明(10)式定义的T是一个紧算子。
定义2 设A,E是Banach空间,设T∶A→E线性;若在E中是紧集,则称T是紧算子,其中B0是A中的单位闭球。
引理1[7]设ξ=ξ1+ξ2=,设e=(0,…,1,...,0)为G中的单位元,则下列结论成立:
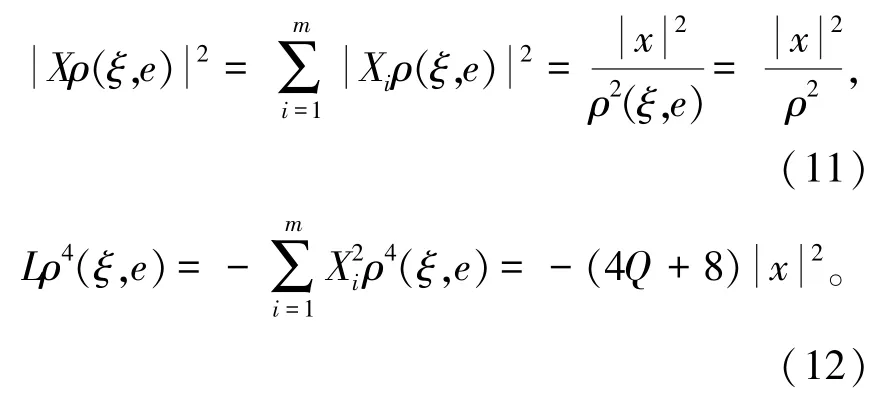
引理2[5]对任意的u,v∈,下列公式成立

定理1 算子T在L2(Ω)上是紧的。
证明 因为

将上式代入(12)式得


由(7)、(8)和(13)式得到
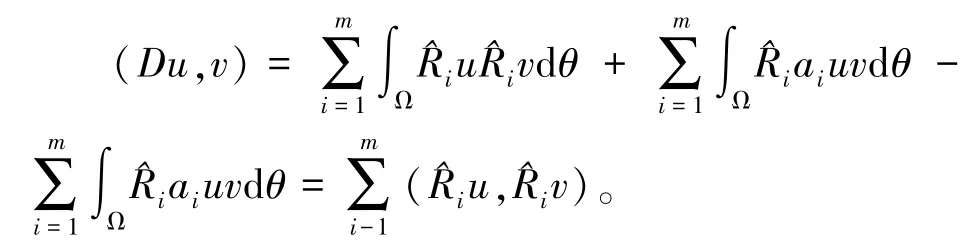

因为

所以

故a(u,v)是连续的。由Poincaré不等式可知


事实上,类似文献[9]中命题3.1(a)的证法,我们选择使得,则有=-Q,由文献[5][6]我们知道在Ω上存在一个非零Radon测度,使得 G上的 Haar测度 d V0=ρQ-1dρdθ。因为u∈C20(Ω),并且u∶∂BG(e,1)→R,所以




最后,我们来验证T是线性的。令f1,f2∈L2(Ω),则f1,f2满足

由(10)式知

再令

当u~∈Ω时,必有

所以


因此T是线性的。
3 T的特征值和特征函数
在上一节,我们针对海森堡型群上的一类边值问题,给出了一个算子T,并且证明了T是一个紧算子。在这一节,我们将进一步研究紧算子T的特征值与特征向量。
引理3[10](Krein-Rutman定理)令Γ⊂L2(Ω)是L2(Ω)中正函数的锥,若T是紧的线性映射,使得T(Γ)⊂Γ,且存在φ∈Γ和ρ>0满足Tφ-ρφ∈Γ,则存在T的一个特征值μ0和与之对应的特征函数u0∈Γ,使得T(u0)= μ0u0,这里μ0=r(T)>0。
引理4[11]P是无界域M上的一个次临界算子,φ∈C(M)是方程Pu=0在M∗1上的一个正解,。如果在M中Pv=f≥0,f∈C(M),,那么在M中v≥0。
定理2 T存在正的特征值和特征函数。
证明 由引理3知,证明的关键是找到满足Tφρφ∈Γ的φ∈Γ及ρ>0。我们令Ω′⊂Ω使得Ω′⊂Ω1⊂Ω,Ω1的边界上没有特征点。我们选择φ≠0,φ∈Γ∩L∞,φ的支集Ζ包含在Ω′中。
由T的定义以及引理4知函数υ=Tφ满足
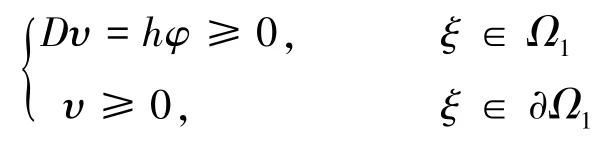
再由强极大值原理可知

所以φ≤‖φ‖L∞。 于是

故

即
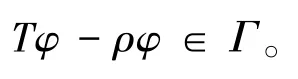
所以φ和ρ满足引理3的条件,又因为T是紧算子,所以由引理3可知:T存在一个正的特征值μ0=r(T)>0及与μ0对应的正特征函数u0∈Γ,使得T(u0)=μ0u0,定理2得证。
4 总结
本文利用极坐标在更广泛的海森堡型群上证明了算子T的紧性,而T的紧性对研究海森堡型群上的一类边值问题的解意义重大。而且进一步证明了紧算子T具有正的特征值和特征向量,该性质将帮助我们研究海森堡型群中无界域上的De Giorgi猜想。
[1]Birindelli I.Hopf’s Lemma and Anti-maximum Principle in General Domains[J].J.Diff.Equations,1995,119:450-472.
[2]Birindelli I,Prajapat J.One dimensional symmetry in the Heisenberg group[J].Annali della Scuola Normale Superiore di Pisa,2001,3:1-17.
[3]Berestycki H,Hamel F,Monneau R.One-dimensional symmetry of bounded entire solutions of some elliptic equations[J].Duke Math.J.,2000,103(3):375-396.
[4]Kaplan A.Fundamental solutions for a class of hypoelliptic PDE generated by composition of quadratic forms[J].Trans.AmerMath Soc.,1980,258:147-153.
[5]Balogh Z M,Tyson JT.Polar coordinates on Carnot groups[J]. Math Z.,2002,241(4):697-730.
[6]Balogh Z M,Tyson J T.Potential Theory in Carnot groups[J]. AMSSeries in Contemporary Mathematics,2003,320:15-27.
[7]Garofalo N,Vassilev D N.Regularity near the characteristic set in the nonlinear Dirichlet problem and conformal geometry of sub-Laplacians[J].Math Ann,2000,318:453-516.
[8]韩军强,钮鹏程.H型群上的偏微分方程[M].西安:西北工业大学出版社,2009:23-28.
[9]Jerison D S.Boundary regularity in the Dirichlet problem for Lbon CR manifolds[J].Comm.Pure.Appl.Math.,1983,36:143-181.
[10]Dong Y.Holder Regularity forWeak Solutions to Divergence From Degenerate Quasilinear Parabolic Systems[J].JMath Anal Appl,2014,410(1):374-375.
[11]Y.Pinchover.Maximum and anti-maximum principles and eigenfunctions estimates via perturbation theory of positive solutions of elliptic equations[J].Math Ann,1999,314:555-590.
(责任编辑:曾 晶)
A Special Operator Defined on Koranyi Unit Sphere
WANG Zhenhua,ZHANGWeiyuan∗,LIYanyan
(School of Mathematics and Information Science,Xianyang Normal University,Xianyang 712000,China)
For a type of boundary-value problem defined on the unbounded domain of Heisenberg type group,a linear operator was constructed,and its compactness,eigenvalue and eigenvector were studied respectively.
embedding theorem;compact operator;eigenvalue and eigenvector
O175.3
A
1000-5269(2016)04-0012-04
10.15958/j.cnki.gdxbzrb.2016.04.02
2015-12-20
国家自然科学基金(11526174);陕西省自然科学基金项目(2015JM1015);陕西省教育厅专项科研项目(2013JK0578);校内项目(06XSYK250;201202012)
王振华(1974-),男,讲师,研究方向:基础数学,Email:mail_wangzhenhua@126.com.
∗通讯作者:张为元,Email:ahzwy@163.com.
