基于多元回归分析的多因子选股模型

黄宏运，王 梅，朱家明

(1.安徽财经大学 金融学院，安徽 蚌埠 233000；2.安徽财经大学 统计与应用数学学院，安徽 蚌埠 233000)



基于多元回归分析的多因子选股模型

黄宏运1，王 梅，朱家明2

(1.安徽财经大学 金融学院，安徽 蚌埠 233000；2.安徽财经大学 统计与应用数学学院，安徽 蚌埠 233000)

针对股票选取的多因子问题，利用MATLAB软件建立股票的基本面指标(市净率、市盈率、资产负债比率等)、技术面指标(当日涨幅、10日涨跌比率ADR、10日相对强弱指标RSI、当日K线值、10日乖离率BIAS、当日OBV和30日RSV等)对相对收益率的多元线性回归模型，并对所建立模型的多重共线性和异方差性进行了适当的检验和改进以给出一个更加合理科学的多因子选股模型．

股票因子；多元回归分析；广义逐步回归；多重共线性；MATLAB

伴随着我国经济的高速发展和资本市场的不断扩展，广大个人与机构投资者对于股票选取方法的需求呈现出日益增长的趋势．由于股票选取的方法有多种，如结合基本面分析、结合技术指标分析等等，为了更多地融入影响股票选取的因子，现今基于因子分析的选股方法越来越受到大家的欢迎．事实上，多因子选股模型是应用比较广泛的一种选股模型，其基本原理就是采用一系列的因子作为选股标准，满足这些因子的股票则被买入，不满足的则卖出．通常来说，多因子选股模型有两种判断方法，一是打分法，二是回归法．

1 数据来源与相关假设

本文的数据来源主要为上海和深圳证券交易所以及同花顺数据中心，数据的格式为2937行11维，分别代表2937只股票和影响每只股票相对收益率的10项影响因子(第11列为对应股票的相对收益率)，为了消除数据数量级与量纲差异对回归模型的影响，对数据进行了适当的归一化处理．为了问题和数据的处理方便，有以下几点假设：①假设所获取的数据真实、准确和可靠．②假设对数据进行的四舍五入不会对回归结果产生影响.③假设短期选取的股票池对于市场来说有效．

2 多元线性多因子选股模型

2.1 研究思路

由于影响股票选取的因子众多，为了综合考虑基本面指标[1]、技术面指标[2]等一级指标中二级因子，分别从各项一级指标中选取了几项具有代表性的二级因子，具体包括市净率、市盈率、资产负债比率、当日涨幅、10日涨跌比率ADR、10日相对强弱指标RSI、当日K线值，10日乖离率BIAS、当日OBV和30日RSV等(后文为了阐述的方便简称各项因子为因子1、因子2、因子3等等)．为了使收益率的衡量更加具有可比性，引入虚拟的被解释变量相对收益率，具体将近期收益率表现出明显上升趋势的股票的相对收益率定义为1，表现出明显下降趋势的股票的相对收益率定义为-1，而表现出横盘震荡或整理状态的股票的相对收益率定义为0．

2.2 研究过程

(1)模型建立.首先以相对收益率为被解释变量建立十个影响因子的多元回归模型[3]，具体模型结果如表1所示.

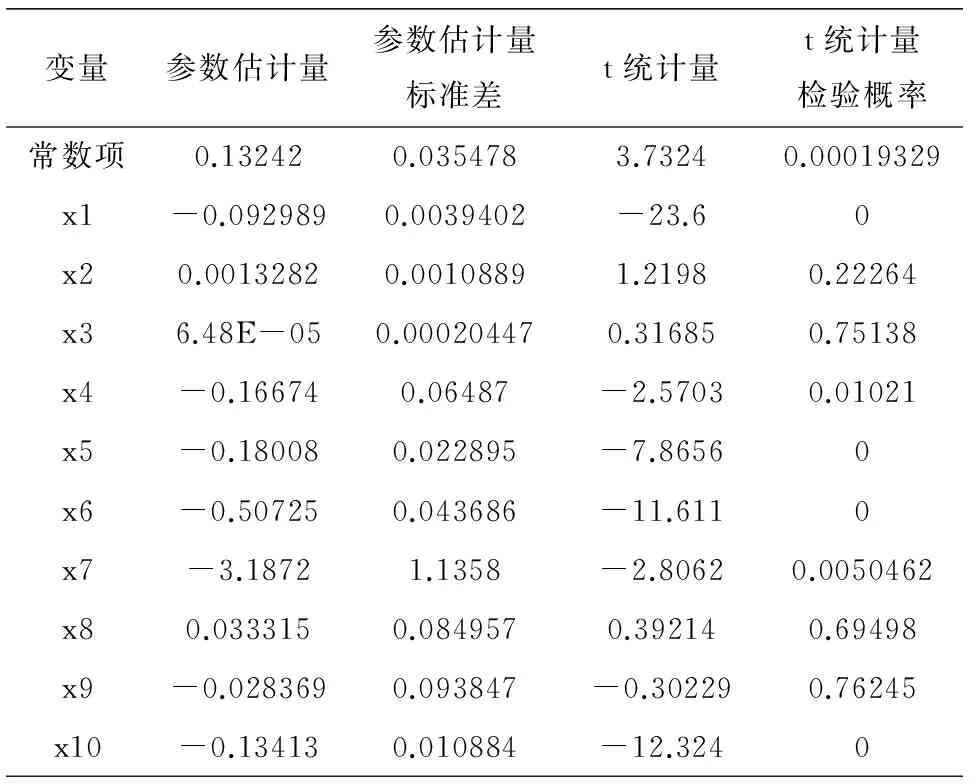
表1 多元回归模型

模型的可决系数R2=81.9%，说明整体股票因子对相对收益率[4]的拟合精度并不是太高，由表1可以看出，在置信度为0.05的水平下，因子x1、x4、x5、x6、x7、x10对于相对收益率的影响显著，也进一步说明再利用上述十项因子实现回归选股时，应对市净率[5]、当日涨幅、10日涨跌比率ADR、10日相对强弱指标RSI、当日K线值和30日RSV予以优先考虑或赋予较多的权重计算相对收益率的大小．

从上述回归模型的结果可以看出，其他四项因子并没有通过显著性检验，但这不表明这些因子对于相对收益率的影响不重要，这主要是由于股票因子之间具有相同的变化趋势，而这无疑会导致回归模型存在严重的多重共线性问题．以下首先利用各因子之间的相关系数对变量之间存在的多重共线性进行检验，然后利用广义线性逐步回归法对模型中的多重共线性问题进行改进．

(2)模型改进.利用MATLAB软件绘制出各因子之间的相关系数热图如图1、图2所示．

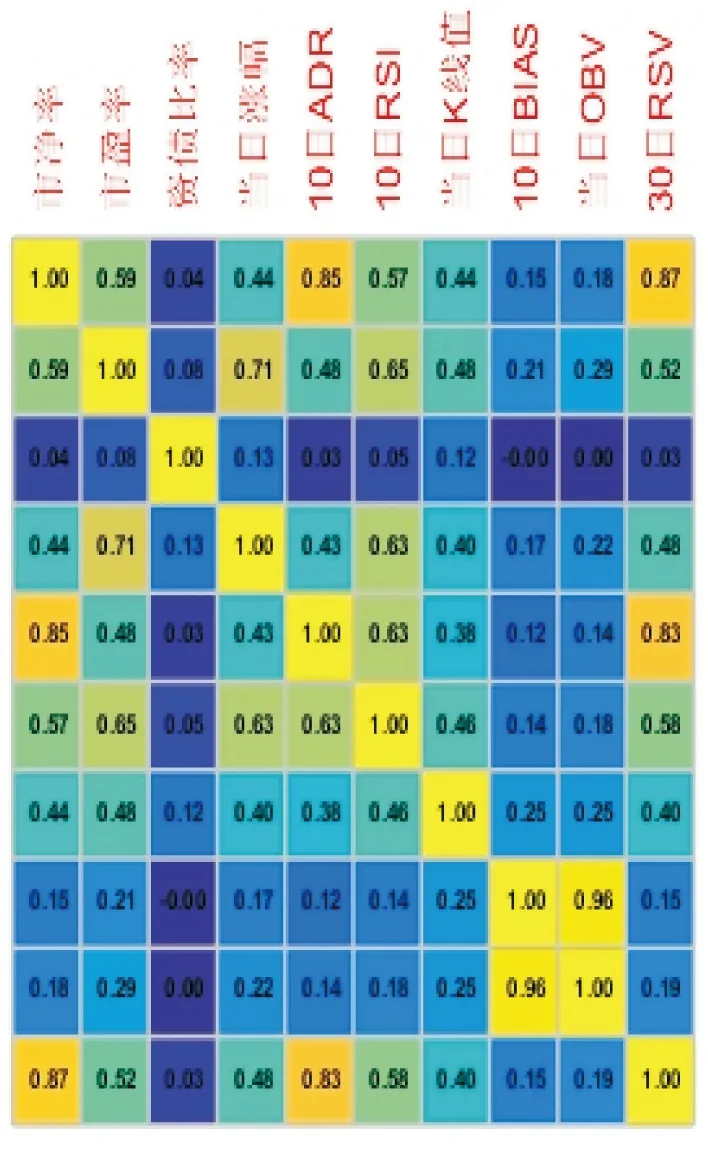
图1 因子相关系数矩形

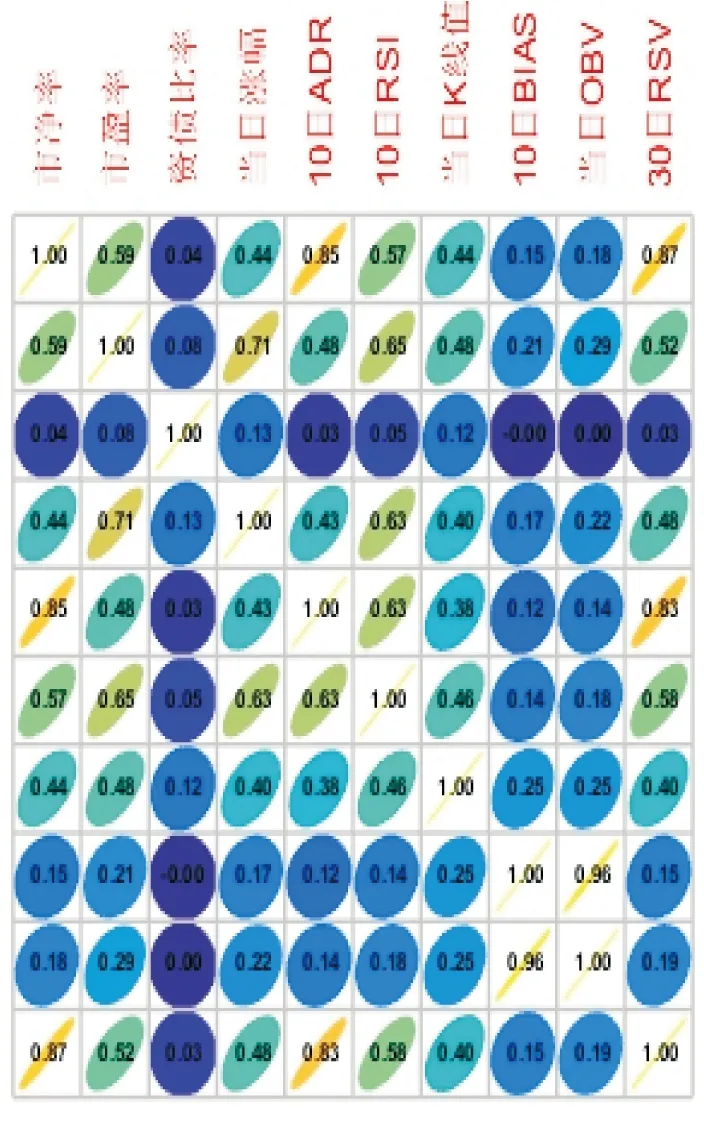
图2 因子相关系数椭圆

从图1、图2可以发现，模型的各因子之间存在着较多的多重共线性问题，如x1与x5、x10，x5与x10,x8与x9等．对于回归模型中存在的多重共线性问题，通常有如下几种处理方法：①剔除不显著变量，此方法可能会导致剔除显著变量进而导致模型的设定误差．②增大样本容量，此方法适用于样本数据较少的情形．③变换模型形式，如采取差分法、对数变换法等重新建立回归模型，此方法可能会导致模型的误差项序列相关，进而违背线性回归模型的相关假设．④逐步回归法，此修正方法的基本思想是先用因变量对每一个所考虑的自变量作简单回归，然后以对因变量贡献最大自变量所对应的回归方程为基础，再逐个引入其余的自变量．

由于逐步回归法不仅可以将统计上不显著的自变量剔除，最后保留在模型中的自变量之间多重共线性不明显，而且对因变量有较好的解释贡献，所以选择逐步回归法对原有模型进行改进．

为了尽量使模型的拟合精度得到提高，首先将样本数据中的一些异常值与离群点剔除，具体结果如图3、图4所示．

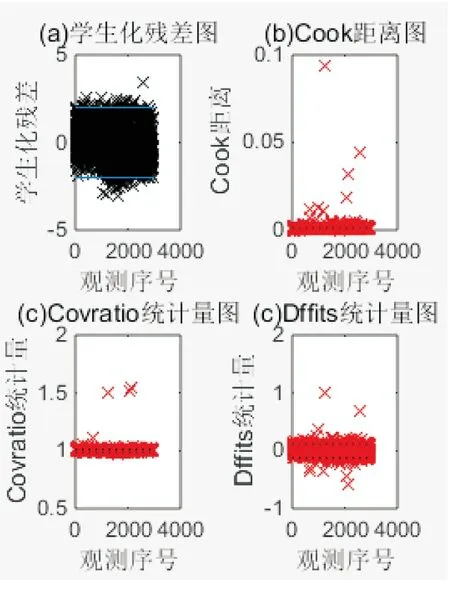
图3 异常值检验

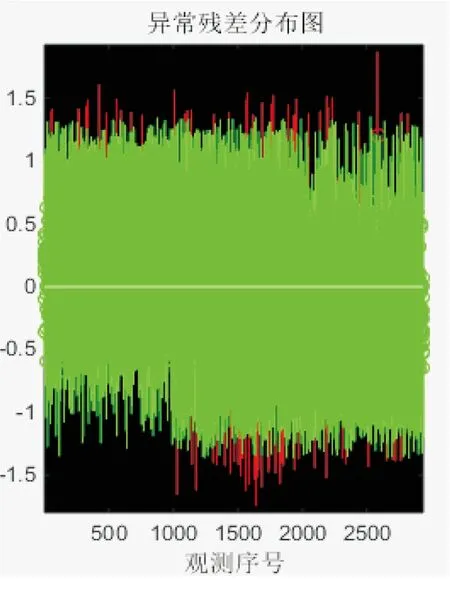
图4 异常值残值分布图

将图2、图3中异常值剔除后，利用广义逐步回归法得到的模型结果，如表2所示．

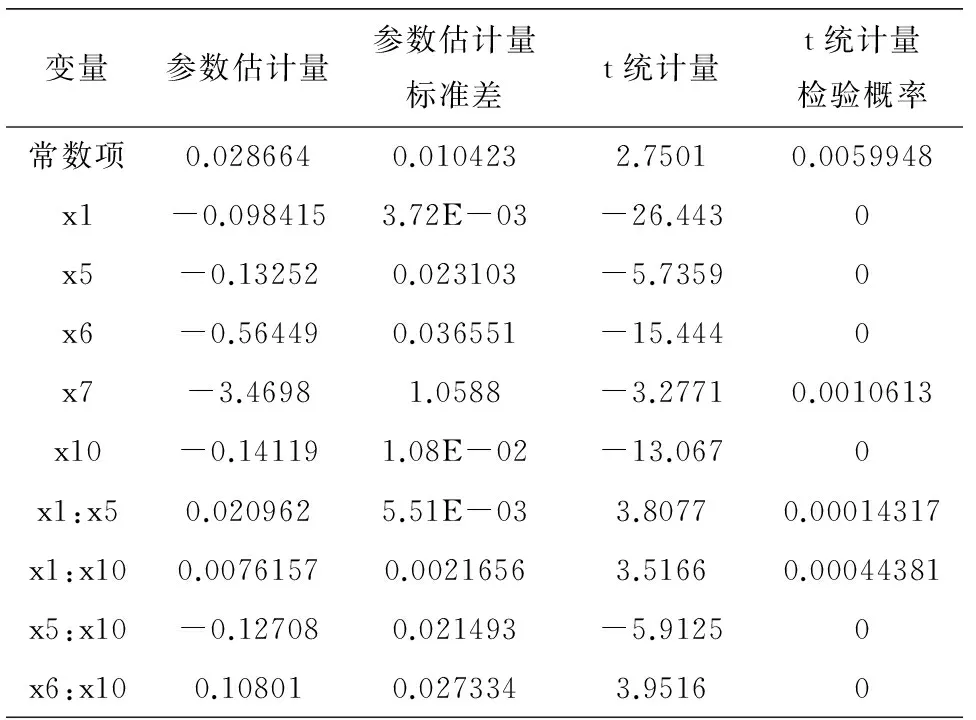
表2 广义逐步回归模型

改进后模型的可决系数R2=92.5%,说明剔除变量后的剩余股票因子对相对收益率的拟合精度得到显著提高，由表2可以看出，利用广义逐步回归法建立模型的t统计量均通过检验(置信水平为0.05)，说明因子x1、x5、x6、x7、x10对于相对收益率的影响显著，并且给出了上述因子交叉项x1x5、x1x10、x5x10和x6x10对于相对收益率的影响关系．

(3)模型应用.利用改进后的模型选取部分样本数据进行检验得到回归结果残差分析如图5、图6所示．

从图5可知，以相对收益率为衡量标准所选股票被明显地分为三部分，其中位于最上面那一部分的股票即对应相对收益率最高的个股，而位于最下面那一部分的股票对应为相对收益率最低的个股，位于中间部分的股票即相对收益率处于最高与最低之间的个股，可以看出，利用上述建立的多因子选股模型可以很好地根据因子因素区分这些股票的相对收益率高低，这对投资者在实际的选股过程中无疑

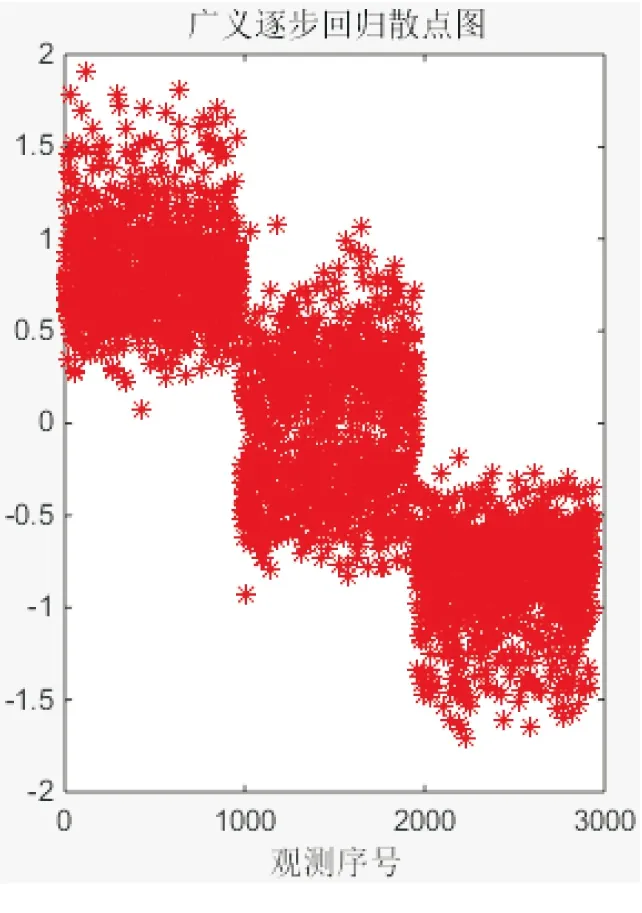
图5 回归预测结果

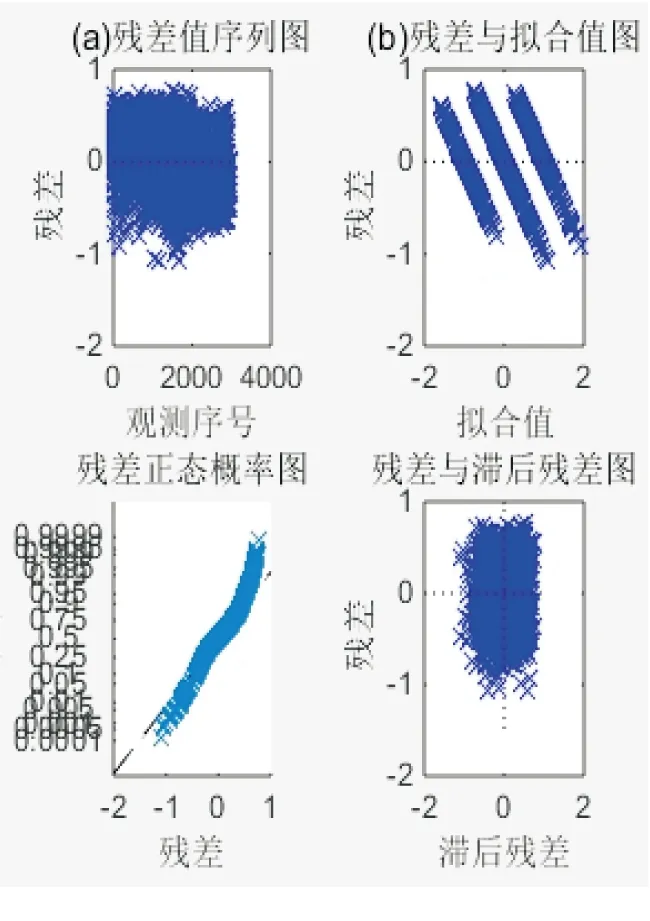
图6 残差分析图

提供了很好的借鉴．从图6可知，实际值与预测值之间的残差项符合正态分布，且基本上可以认为残差项满足无自相关和同方差假定．

3 结论

本文利用多元回归分析理论建立了相对收益率对十项股票因子市净率、市盈率、资产负债比率、当日涨幅、10日涨跌比率ADR、10日相对强弱指标RSI、当日K线值、10日乖离率BIAS、当日OBV和30日RSV的多因子选股模型，不仅对现实中的优质选股问题提供了一定的借鉴方法，而且可以将上述模型进行推广运用到公司财务预警、水质污染评估、土地储备风险评估等各个领域．

[1]张铁涛,周红.财务报表分析[M].北京:清华大学出版社,2012.

[2]康凯彬.从零开始学操盘[M].北京:中国纺织出版社,2015.

[3]戴明强,宋业新.数学模型及其应用[M].北京:科学出版社,2015.

[4]李健.金融学[M].北京:高等教育出版社,2014.

[5]戴国强.货币银行学[M].上海:上海财经大学出版社,2012.

(责任编辑:陈衍峰)

10.13877/j.cnki.cn22-1284.2016.08.014

2016-03-12

国家自然科学基金资助项目“随机动力系统的非一致指数二分性及其数值模拟”(11301001)

黄宏运,安徽合肥人,安徽财经大学金融学院在读；李晓杰,女,安徽阜阳人；朱家明,安徽泗县人,副教授.

F064.1、O129

A

1008-7974(2016)04-0044-03