转捩模型在翼型气动性能预测中的应用研究

张瑞民，时晓天

(中国航天空气动力技术研究院 第二研究所，北京 100074)



转捩模型在翼型气动性能预测中的应用研究

张瑞民，时晓天

(中国航天空气动力技术研究院 第二研究所，北京 100074)

边界层转捩位置的准确预测对于提高飞行器气动性能的预测精度具有重要意义。选取与k-ωSST湍流模型相耦合的γ-Reθt模型，以零压力梯度平板为研究对象，通过求解基于有限体积法的雷诺平均N-S方程验证该模型自动捕捉流动转捩的准确性；将该模型应用于传统有压力梯度的NACA 0012翼型的流场特性和气动性能的研究中，并与原始k-ωSST模型的计算结果及全湍流试验数据进行比较。结果表明：远场边界距离对翼型阻力系数有较大的影响；与无转捩模型相比，γ-Reθt转捩模型对翼型阻力系数的预测精度有一定程度的提高；对于二维模型，γ-Reθt转捩模型难以捕捉翼型表面的三维效应和非定常分离特性。

转捩；湍流；翼型；平板；气动特性

0 引 言

在航空航天领域，关于层流边界层向湍流边界层转捩的研究，始终是研究的热点和难点。转捩的起始位置和长度对粘性阻力、壁面传热以及边界层分离特性具有强烈的影响。例如，在民用运输机中，摩擦阻力占总阻力的50%[1]，而边界层内层流的摩擦阻力却比湍流的摩擦阻力小得多[2]。因此，开展有关边界层转捩预测的研究对于飞机、宇宙飞船、旋翼桨叶和风轮机叶片的设计工作具有重要意义。

目前，已成功应用于边界层流动转捩数值模拟的方法包括直接数值模拟、大涡模拟、en方法、低雷诺数湍流模型和γ-Reθt转捩模型。其中，γ-Reθt模型是由R.B.Langtry等[3]发展的一种基于经验关系、只依赖于流场当地变量的两方程转捩模型，它与k-ωSST湍流模型相耦合，利用应变率雷诺数代替动量厚度雷诺数来触发转捩，避免了积分边界层厚度问题。

γ-Reθt转捩模型[4-5]集合了转捩经验关系式和低雷诺数湍流模型的优势，能够适应现代CFD的发展，在工程中得到了广泛应用。Niels N.Sørensen[6]补充了前期未公布的经验关系；S.Medida等[7]和杜磊等[8]分别将γ-Reθt模型与S-A湍流模型相结合，并进行了耦合模拟验证；C.Seyfert等[9]基于γ-Reθt模型，发展了可处理横流不稳定的转捩模型；张玉伦等[10]开展了模型的标定、应用以及改进工作；肖良华等[11]将γ-Reθt模型应用于高升力构型的数值模拟中；伍斯等[12]将γ-Reθt模型应用于不同类型的翼型边界层转捩预测；乔磊等[13]针对γ-Reθt模型模拟航空外流转捩时存在湍流区摩擦力系数二次异常跃升问题进行了研究和改进。

本文在上述研究的基础上，首先以零压力梯度平板为研究对象，验证γ-Reθt模型捕捉流动转捩的准确性；然后利用γ-Reθt模型预测典型的有压力梯度的NACA 0012翼型表面的边界层转捩位置，并给出该翼型在不同攻角下的阻力系数，进而得到有意义的结论。

1 数值方法

1.1 转捩模型方法

γ-Reθt转捩模型包含间歇因子γ和转捩动量厚度雷诺数Reθt的两个输运方程。间歇因子用来描述边界层流动为层流或湍流的状态，并控制转捩点下游湍动能生成项的开启。间歇因子无量纲输运方程的守恒形式[14]为

Pγ-Eγ

(1)

Pγ=ca1FlengthρS(γFonset)0.5(1-ce1γ)

(2)

Eγ=ca2FturbρΩγ(ce2γ-1)

(3)

式中：ρ为气流的密度；μ为层流黏性系数；μt为湍流黏性系数；S为应变率的模；Ω为涡量的模；Flength为转捩区的长度；Fonset用来控制Pγ的开启；Fturb则用来在边界层外和粘性底层关闭Eγ。Flength是经验关联函数，是转捩动量厚度雷诺数Reθt的函数。

F.R.Menter等[14]认为转捩动量厚度雷诺数(Reθt)是当地湍流度Tu和压力梯度因子λθ的函数，完整的经验关联公式为

Reθt=E(Tu)·F(λθ)

(4)

(5)

(6)

(7)

式中：U为当地速度；θ为动量厚度；s为流线的弧长；F(λθ)为压力梯度的影响。

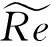
(8)

(9)

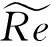
γ-Reθt转捩模型中两个输运方程的作用是获得间歇因子γ，使用间歇因子来修正标准k-ωSST模型中k方程的生成项、破坏项和混合函数[3]，而后与湍流模型联合来模拟转捩过程。

1.2 控制方程

流场计算采用基于压力和速度耦合的SIMPLE算法来求解定常可压缩N-S方程，即

div(ρUφ)=div(Γφgradφ)+Sφ

(10)

式中：Γφ为扩散系数；Sφ为源项；φ为通用项。

边界条件选用压力远场和无滑移壁面边界条件，方程的离散采用有限体积法，为了保证计算求解的稳定和收敛，所有方程的对流项采用二阶迎风格式，扩散项采用中心差分格式。

1.3 湍流模型

选用k-ωSST两方程湍流模型，运动方程为

Gk-Yk+Sk

(11)

Yω+Dω+Sω

(12)

式中：Gk、Gω分别为k和ω的生成项；Yk、Yω分别为由湍流引起的k和ω的耗散项；Γk、Γω分别为k和ω的有效扩散系数。

其中，

(13)

μt=ρk/{ωmax[1/α*,SF2/(α1ω)]}

(14)

式中：α1为常数；F2为混合函数。

在高雷诺数下，间歇系数α*=1，此时流动为湍流，若考虑低雷诺数转捩的影响，间歇系数α*的表达式为

(15)

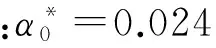
2 算例与分析

2.1 零压力梯度平板

以零压力梯度平板为研究对象，对所采用的模型模拟转捩流动的能力进行验证。网格划分和边界条件如图1所示，沿平板流向布置270个网格节点，沿法向布置100个节点，且物面法向第一层网格距离为1.0×10-5m，保证y+≤1.0，法向增长率为1.1。计算条件如表1所示。

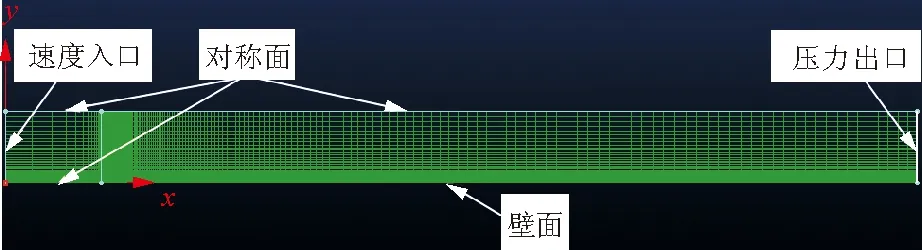
图1 计算网格和边界条件

在四种不同的入口来流条件下，平板表面摩擦力系数的模型预测结果与测试数据的对比如图2所示。

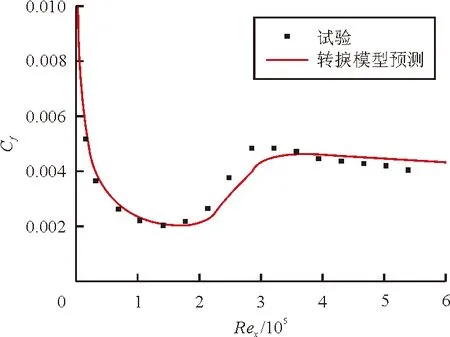
(a) T3A

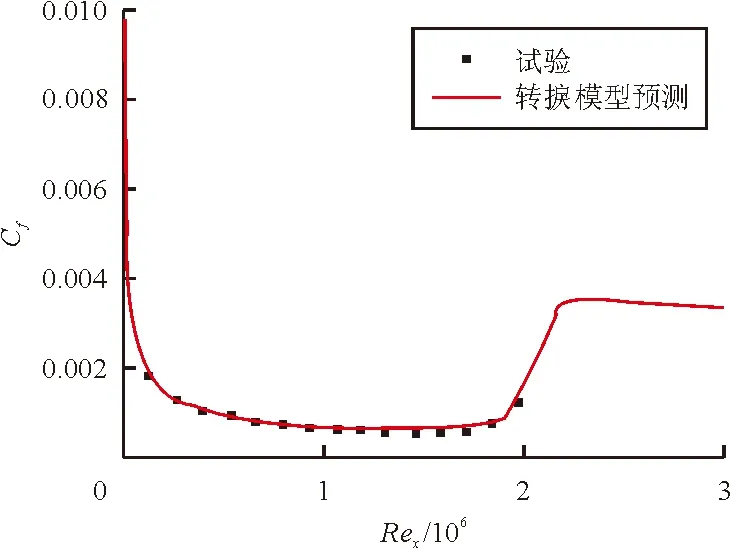
(b) T3A_

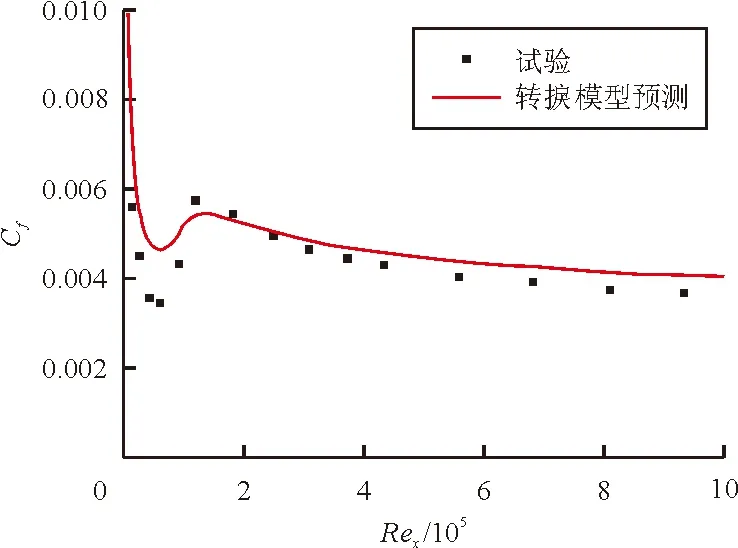
(c) T3B

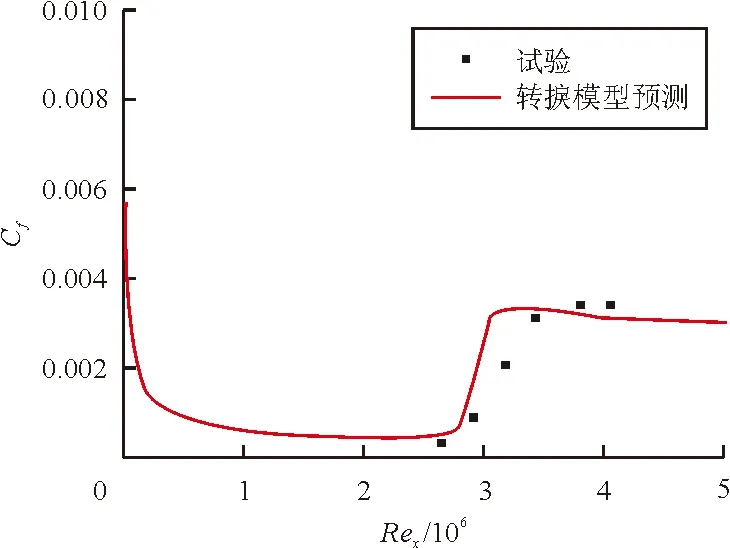
(d) S&K

从图2可以看出：模型预测结果与测试数据符合较好，随着入口来流湍流度的增加，转捩位置逐渐移向更低的雷诺数。

2.2 有压力梯度的NACA 0012翼型

以有压力梯度的NACA 0012翼型为研究对象，选取2.1节已验证过的转捩模型，预测不同攻角下翼型上、下表面的边界层转捩位置，并对该翼型的流场特性和气动性能进行分析。

采用转捩模型的目的是提高阻力计算的精度，高升力翼型的远场边界距离对气动特性，尤其是阻力特性影响显著[15]，该结论对NACA 0012翼型同样适用，因而选择不同的远场边界对NACA 0012翼型的阻力特性进行研究。基准网格如图3～图4所示，远场边界距离翼面为弦长c的20倍。计算采用压力远场，翼面边界为固壁边界，采用无滑移边界条件。壁面第一层网格厚度为1.0×10-5m，保证y+≤1.0，法向增长率为1.1。来流计算条件：Ma=0.3，Re=3×106；湍流参数的取值：k=(0.001×U∞)2，ω=k/μt，μt=0.009μ。

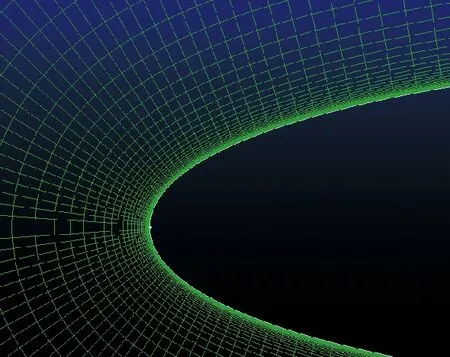
图4 局部放大图

8°攻角下不同远场条件下的翼型阻力系数如表2所示，可以看出：阻力随着远场边界的扩大单调减小，接近200c后开始收敛；与试验测试值相比，误差从22.77%逐渐减小到4.95%。因此，在后续的研究中，远场边界采用弦长的200倍。

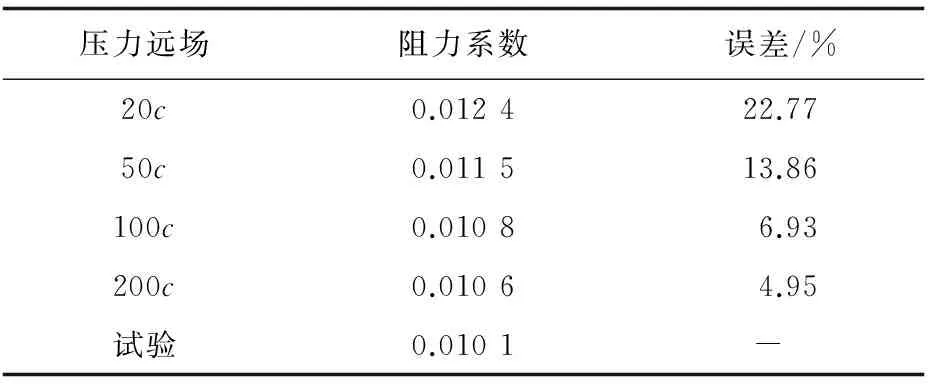
表2 不同远场边界条件下的阻力系数

NACA 0012翼型在不同攻角下壁面边界层的转捩位置将分别通过间歇因子云图和摩擦力系数图给出。0°、3°、5°、8°攻角下的间歇因子云图如图5所示，白色圆圈表示转捩发生的位置，转捩因子从0逐渐跃升到1标志着转捩开始发生；x、y分别表示翼型坐标点沿轴向和法向的距离；c表示翼型的弦长。相应的摩擦力系数分布图如图6所示。转捩发生位置的预测结果与试验数据的对比如表3所示。

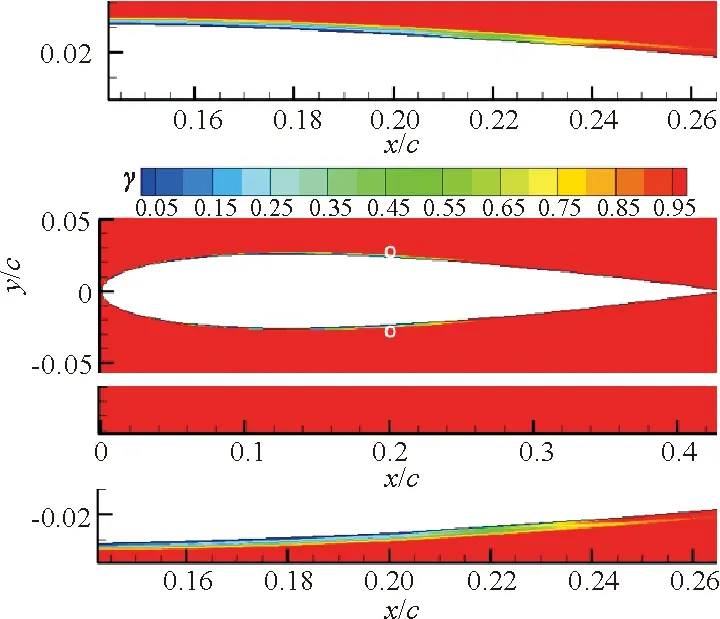
(a) 攻角为0°

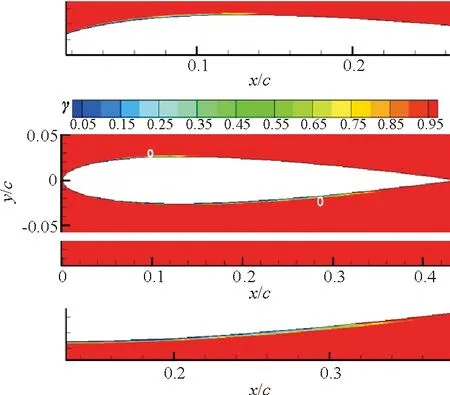
(b) 攻角为3°

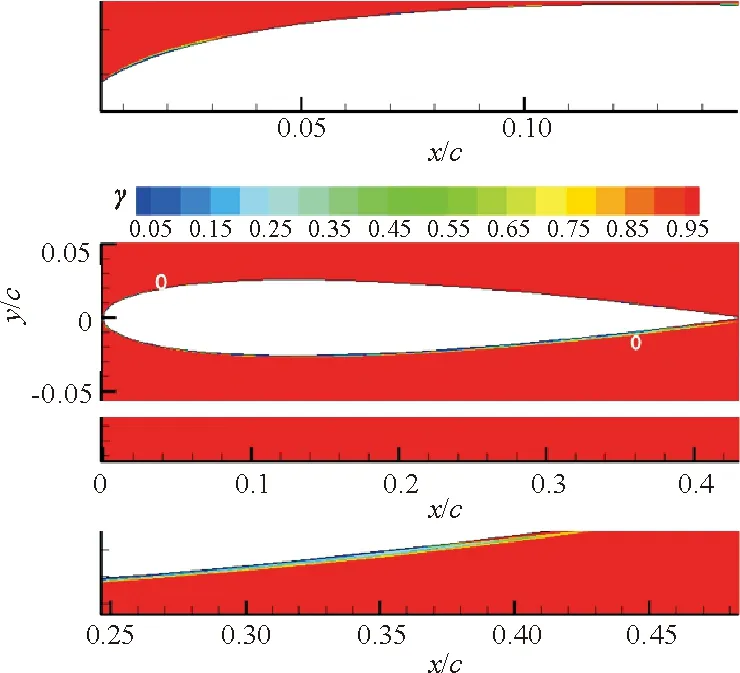
(c) 攻角为5°

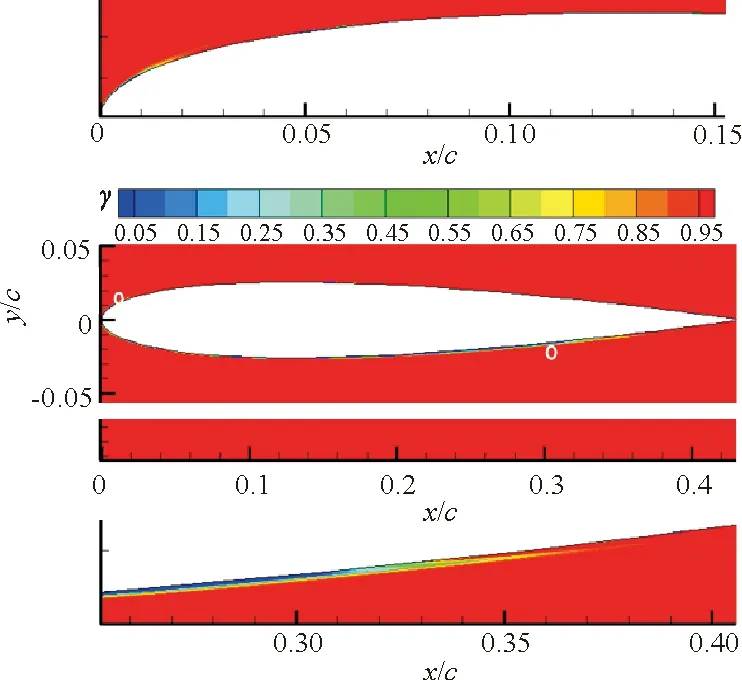
(d) 攻角为8°

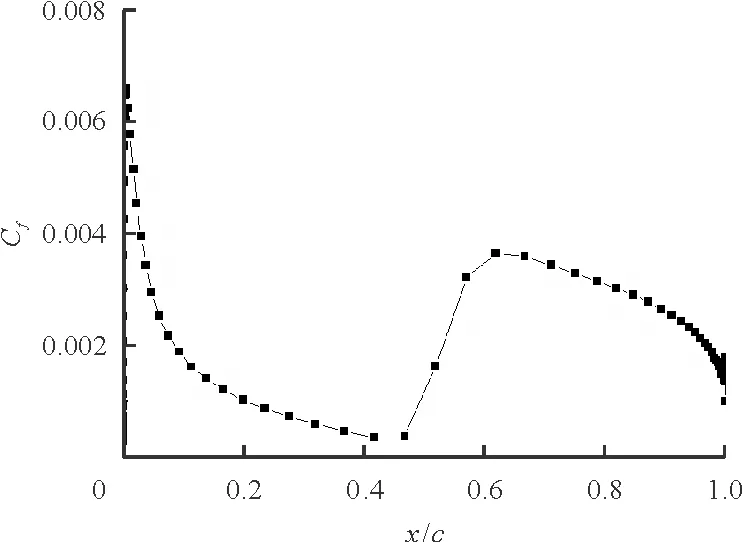
(a) 攻角为0°

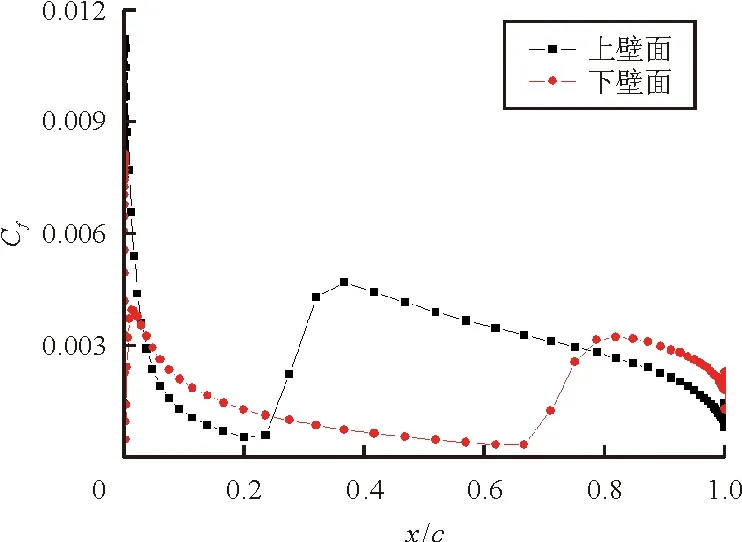
(b) 攻角为3°

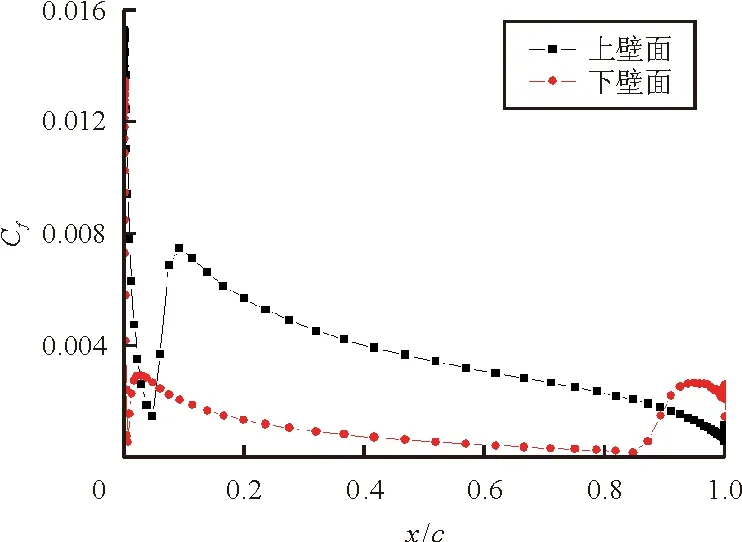
(c) 攻角为5°

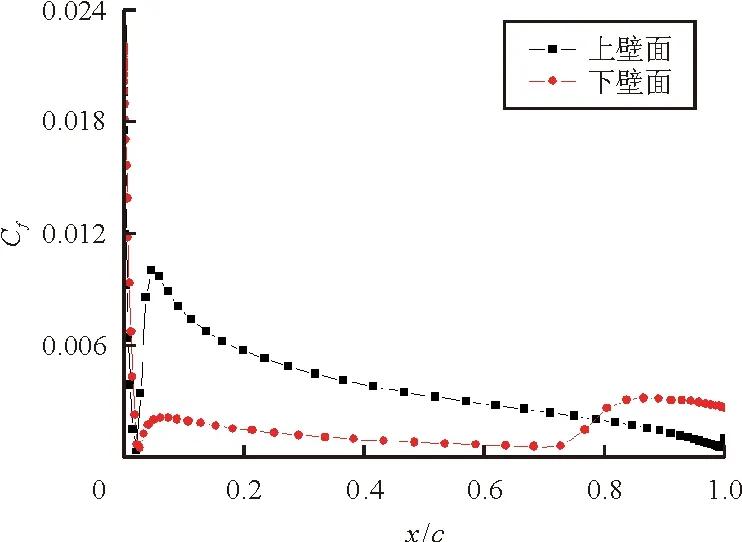
(d) 攻角为8°

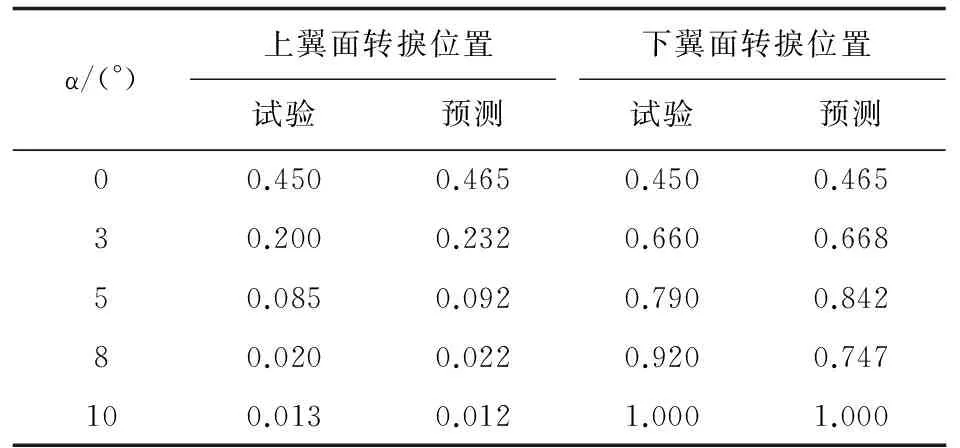
α/(°)上翼面转捩位置下翼面转捩位置试验预测试验预测00.4500.4650.4500.46530.2000.2320.6600.66850.0850.0920.7900.84280.0200.0220.9200.747100.0130.0121.0001.000

从表3可以看出：除8°攻角下的翼型下表面外，模型预测的转捩起始位置与试验数据吻合较好。

不同攻角下翼型上、下表面的压力系数分布如图7所示。

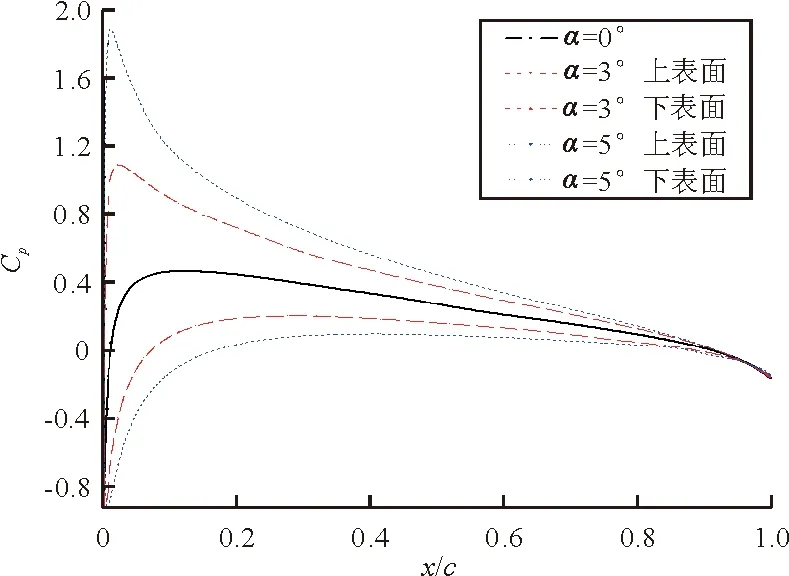
图7 不同攻角下翼型表面的压力系数分布图

从图7可以看出：当翼型攻角逐渐增大时，翼型上表面的顺压梯度区减小，逆压梯度区的压力梯度增加，导致流动提前转捩；而下表面的顺压梯度区逐渐增大，逆压梯度区的压力梯度减小，从而推迟了转捩的发生。因此，当攻角逐渐增大时，翼型上表面的转捩起始位置逐渐前移，下表面的转捩起始位置逐渐靠后，这也与表3中给出的结果完全相符。

数值计算得到的阻力系数的结果如图8所示。

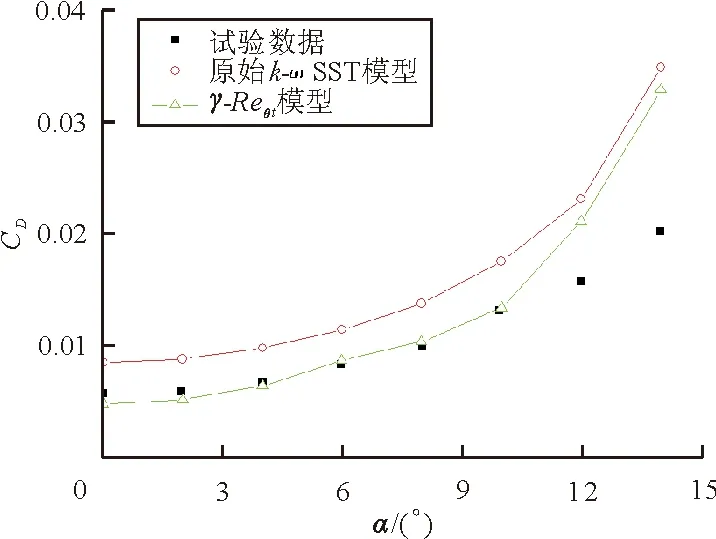
图8 翼型阻力系数随攻角的变化

从图8可以看出：当迎角小于12°时，翼型的阻力系数与试验数据[16]吻合得很好；当迎角等于12°或者更大时，与原始无转捩k-ωSST模型的预测结果相比，阻力系数仍有一定程度的提高，但与试验值相比，本文的计算结果偏大，原因可能是所采用的数值方法对于大攻角下阻力系数的预测准确度还不够。

3 结 论

(1)γ-Reθt转捩模型能够较好地捕捉零压力梯度平板的转捩位置和转捩发展过程。

(2) 远场边界距离对翼型阻力系数有较大影响，故在开展气动特性研究之前应进行细致地对比分析和选择。

(3)γ-Reθt转捩模型能够较好地预测有压力梯度的NACA 0012翼型的转捩位置和气动特性，且与无转捩模型相比，其阻力系数的模拟精度有一定程度的提高。

(4)γ-Reθt转捩模型尚不完善，二维模型无法准确地捕捉翼型表面的三维效应和非定常分离特性，在今后的工作中仍需进一步研究。

[1] Joslin Ronald D. Aircraft laminar flow control[R]. USA: NASA Langley Technical Report Server, 1998.

[2] Green J E. Laminar flow control-back to the future?[C]. AIAA-2008-3738, 2008.

[3] Langtry R B, Menter F R. Correlation-based transition modeling for unstructured parallelized computational fluid dynamics codes[J]. AIAA Journal, 2009, 47(12): 2894-2906.

[4] 孟德虹, 张玉伦, 王光学, 等.γ-Reθt转捩模型在二维低速问题中的应用[J]. 航空学报, 2011, 32(5): 792-801. Meng Dehong, Zhang Yulun, Wang Guangxue, et al. Application ofγ-Reθttransition model to two-dimensional low speed flows[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(5): 792-801.(in Chinese)

[5] 王刚, 刘毅, 王光秋, 等. 采用γ-Reθt模型的转捩流动计算分析[J]. 航空学报, 2014, 35(1): 70-79. Wang Gang, Liu Yi, Wang Guangqiu, et al. Transitional flow simulation based onγ-Reθttransition model[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(1): 70-79.(in Chinese)

[7] Medida S, Baeder J D. Application of the correlation-based gamma-Rethetat transition model to the Spalart-Allmaras turbulence model[C]. AIAA-2011-3979, 2011.

[8] 杜磊, 宁方飞. 基于S-A湍流模型和间歇因子输运方程的转捩流数值模拟[J]. 航空动力学报, 2015, 30(10): 2450-2461. Du Lei, Ning Fangfei. Numerical simulation of transition flows based on S-A turbulence model and intermittency transport equation[J]. Journal of Aerospace Power, 2015, 30(10): 2450-2461.(in Chinese)

[9] Seyfert C, Krumbein A. Correlation-based transition transport modelling for three-dimensional aerodynamic configurations[R]. AIAA-2012-0448, 2012.

[10] 张玉伦, 王光学, 孟德虹, 等.γ-Reθt转捩模型的标定研究[J]. 空气动力学学报, 2011, 29(3): 295-301. Zhang Yulun, Wang Guangxue, Meng Dehong, et al. Calibration ofγ-Reθttransition model[J]. Acta Aerodynamica Sinica, 2011, 29(3): 295-301.(in Chinese)

[11] 肖良华, 肖志祥, 王丽莎, 等. 高升力多段机翼的转捩预测研究[J]. 中国科学: 物理学·力学·天文学, 2012, 42(3): 271-281. Xiao Lianghua, Xiao Zhixiang, Wang Lisha, et al. Transition prediction of high-lift wing[J]. Scientia Sinica: Physica, Mechanica & Astronomica, 2012, 42(3): 271-281.(in Chinese)

[12] 伍斯, 高正红. 翼型几何模型对边界层转捩预测精度的影响[J]. 航空工程进展, 2015, 6(3): 287-296. Wu Si, Gao Zhenghong. Influence of airfoil geometry model on boundary layer transition prediction accuracy[J]. Advances in Aeronautical Science and Engineering, 2015, 6(3): 287-296.

[13] 乔磊, 白俊强, 华俊, 等.γ-Reθt转捩模型的改进和验证[J]. 航空动力学报, 2015, 30(10): 2488-2497. Qiao Lei, Bai Junqiang, Hua Jun, et al. Improvement and verification ofγ-Reθttransition model[J]. Journal of Aerospace Power, 2015, 30(10): 2488-2497.

[14] Menter F R, Langtry R B, Likki S R, et al. A correlation-based transition model using local variables-part Ⅰ: model formulation[J]. Journal of Turbomachinery, 2004, 128(3): 413-422.

[15] Rumsey C L, Ying S X. Prediction of high lift: review of present CFD capability[J]. Progress in Aerospace Sciences, 2002, 38(2): 145-180.

[16] Johansen J, Soacut J N. Prediction of laminar/turbulent transition in airfoil flows[J]. Journal of Aircraft, 2015, 36(4): 731-734.

(编辑：马文静)

Research on Application of Transition Model in Prediction of Airfoil Aerodynamic Characteristics

Zhang Ruimin， Shi Xiaotian

(The Second Research Institute, China Academy of Aerospace Aerodynamics, Beijing 100074, China)

It is of important significance for improving the prediction accuracy of aircraft aerodynamic performance to predict the transition position of the boundary layer accurately. Selecting theγ-Reθtmodel coupled withk-ωSST turbulence model and taking no-pressure-gradient plane as an example, the capability of this model for trapping flow transition automatically is verified. Then the model is applied to study the flow characteristics and aerodynamic performance of NACA 0012 airfoil with pressure gradient, the results from which are compared with the computational results from originalk-ωSST model and the test data of complete turbulence model. The study shows that far-field boundary has a great impact on airfoil drag coefficient. Compared to no-transition model,γ-Reθttransition model is of some improvement on predicting airfoil drag coefficient. It is difficult forγ-Reθttransition model to simulate 3-d airflow field and separate characteristics of 2-d model.

transition; turbulent flow; airfoil; plane; aerodynamic characteristics

2016-06-15；

2016-06-29

时晓天,xxtshi@163.com

1674-8190(2016)04-426-07

V211.3

A

10.16615/j.cnki.1674-8190.2016.04.005

张瑞民(1980-)，男，博士，高级工程师。主要研究方向：非定常空气动力学、非线性飞行动力学、飞行器结冰模拟、动力学仿真等。

时晓天(1981-)，男，博士，高级工程师。主要研究方向：空气动力学、计算流体力学。