反比例函数研究提升思维水平和解题能力
2016-12-17江苏省扬州市广陵区头桥中学225109
江苏省扬州市广陵区头桥中学(225109)
孙 静●
反比例函数研究提升思维水平和解题能力
江苏省扬州市广陵区头桥中学(225109)
孙 静●
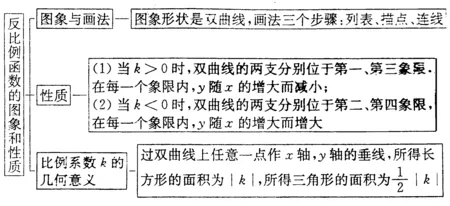
反比例函数一般可表示为y=k/x(k是常数k≠0).反比例函数解析式也可写成y=kx-1的形式,自变量x的取值范围是x≠0的一切实数,函数值取值范围也是x≠0的一切实数反比例函数的图象是双曲线,它有两个分支,这两个分支分别位于第一第三象限或第二第四象限,它们关于原点对称,由于自变量x≠0函数值y≠0,因此它的图象与x轴y轴都没有交点,即双曲线的两个分支无限接近坐标轴,但永远与坐标轴不相交.本文对反比例的图象与性质,反比例函数与一次函数的图象的综合应用,反比例函数图象与有关面积问题举例探讨,供读者参考.
双曲线;反比例图象性质;反比例系数K的几何意义
一、反比例函数的图象与性质
A.y2 C.y1 解析1(性质法) 当k<0时,反比例函数的图象在第二、第四象限,且在每个象限内,y随x的增大而增大,此题中需要注意的是(x1,y1),(x2,y2),(x3,y3)不在同一象限内,因为k=-m2-1=-(m2+1)<0,所以函数图象在第二、第四象限内,所以y2>y1>0.因为x3>0,所以(x3,y3)在第四象限内,所以y3<0,所以y3 比较函数值的大小时,在同一分支上的点可以通过比较其横坐标的大小来判断函数值的大小,不在同一分支上的点,依据与x轴的相对位置来进行函数值大小的比较.特殊值法简单直接,图象法形象、直观,是解决此类题目的常用方法. (1)求反比例函数和一次函数的解析式; (2)根据图象写出使得反比例函数的值大于一次函数的值的x的取值范围. 分析 (1)由点N可求出反比例函数的解析式,进而可求出点M的坐标.由N,M两点可求出一次函数解析式. (2)由y=k/x的图象与y=ax+b的图象的交点进行分析,找到y=k/x的图象在y=ax+b的图象的上方时对应的x的取值范围即可. ∵A,B两点坐标为A(0,2),B(0,-2) ∴AB=4. G632 B 1008-0333(2016)21-0034-01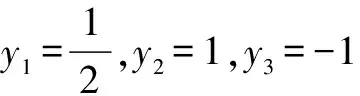
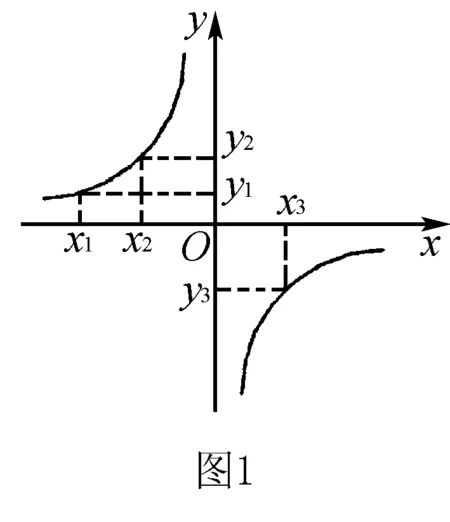

二、反比例函数与一次函数的图象的综合应用
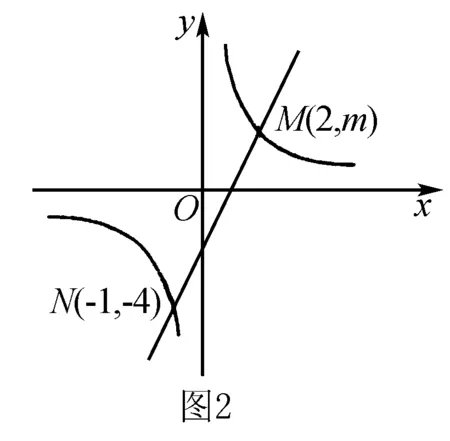

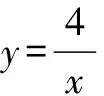
三、反比例函数图象与有关的面积问题
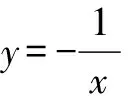

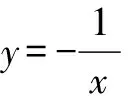
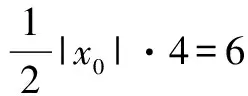
四、重点内容小结