一道高考题的解法探究

雷 波

(重庆市巴南区教师进修学校，401320)



○解题研究○

一道高考题的解法探究

雷 波

(重庆市巴南区教师进修学校，401320)

2016年全国高考数学卷Ⅱ第20题是一道关于椭圆的问题.它除了考查直线和椭圆的基础知识外,还考查了函数与方程的思想、数形结合的思想、分类与整合的思想、化归与转化的思想、特殊与一般的思想.其参考答案也是解析几何的通性通法,但从极坐标和参数方程的角度还有三种不同解法.现把题目和三种不同解法提供如下,供同行参考.

(1)当t=4,|AM|=|AN|时,求∆AMN的面积;

(2)当2|AM|=|AN|时,求k的取值范围.

解法1 (从极坐标的角度)

设椭圆E的顶点A为极点,AO为极轴(O为原直角坐标系原点)建立极坐标系,可得椭圆E的极坐标方程为

∵ tan θ1=k,

(1)当t=4,|AM|=|AN|时,由椭圆的对称性知k=1,

(2)当2|AM|=|AN|时,有

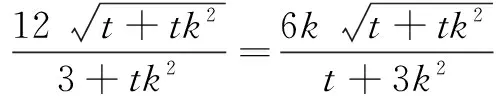
即 t(k3-2)=6k2-3k.

解法2 (从参数方程角度)

将椭圆E的方程化为参数方程

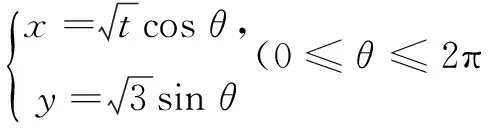
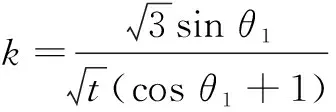
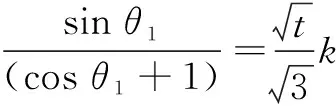
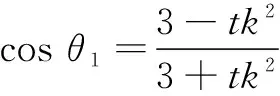
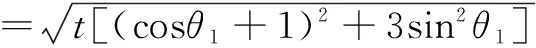
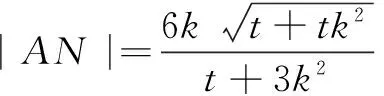
以下解法与解法1相同.

解法3 (从变换的角度)

则椭圆E变换为单位圆

x′2+y′2=1；

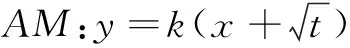
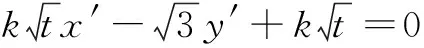
根据线段变换前后的关系,有

设圆心O′(0,0)到直线A′M′的距离为d,则由点到直线的距离公式,得

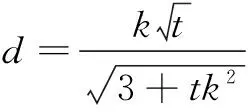
因为在圆O′中有

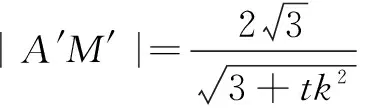
以下解法与解法1相同.