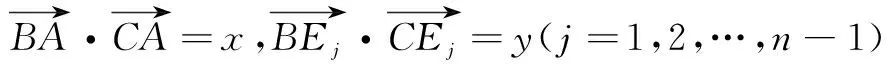一道不等式问题的微探究

汪承兵

(浙江省平湖市当湖高级中学，314200)



○数学探究○

一道不等式问题的微探究

汪承兵

(浙江省平湖市当湖高级中学，314200)

数学教育家G·波利亚曾提出,教师 “应该能够拿出一个有意义的但又不太复杂的题目,去帮助学生发掘问题的各个方面,使得通过这道题,就好像通过一道门户,把学生引入一个完整的理论领域．”

问题 已知x,y是实数,若4x2+y2+xy=1,求2x+y的最大值.

笔者在高二迎考复习时发现学生对基本不等式这一节内容掌握得不很好,表现在学生不知道怎么使用基本不等式,有些即使用了也存在着逻辑错误．本文想通过对上面这一问题的探究,发挥问题的教学功能,使学生清楚基本不等式的思维特征,系统掌握相应的知识,形成能力．

一、基本不等式解题的理论基础

当且仅当a=b时取“=”号；

变形2 a2+b2≥2ab(a,b∈R)，

当且仅当a=b时取“=”号；

当且仅当a=b时取“=”号；

变形4 4ab≤(a+b)2≤2(a2+b2)(a,b∈R)，当且仅当a=b时取“=”号.

基本不等式及其变形不仅揭示了ab、a+b、a2+b2这三者之间的关系,而且在求最值的过程中,还给我们指明了方向．

二、基本不等式解题的模型探究

模型1 找定值

注意应用基本不等式的条件:一正、二定、三相等.“一正”:使用基本不等式时,各项必须为正数;“二定”:若积为定值,则和有最小值;若和为定值,则积有最大值;“三相等”:等号能够成立．解决这类问题的关键是找定值,然而有些问题不能直接看到定值,无法运用基本不等式求解,此时我们需要通过化归思想和初等变形的手段想办法产生定值．

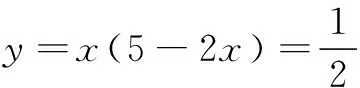
模型2 找匹配

对于本文开始的问题:求2x+y的最大值,如果还是按照模型1的思维,应该找积是定值，然而模型1积为定值,和应该有最小值，问题中是求和的最大值,逻辑上有错误;其次是已知条件4x2+y2+xy=1,既有和的形式又有积的形式,无法找到和或者积是定值，此时我们应该换一种思维,寻找条件和结论之间的联系．从条件中可以找到结论的影子(条件和结论匹配),所以将条件改写成(2x+y)2-3xy=1．我们的目标是求2x+y,所以条件中要保留2x+y；积3xy向和2x+y转化．经过思考有了下面的解法．

解法1 (基本不等式法)

∵ 4x2+y2+xy=1,

∴ (2x+y)2-3xy=1,

把2x+y看成整体,整理得

基本不等式及其变形揭示了ab、a+b、a2+b2这三者之间的关系.在解决问题时我们需要观察条件和结论是否匹配,同时结合ab、a+b、a2+b2的放缩关系,有目的地在三者之间进行转化．学生往往不注意或不容易找到基本不等式的内在逻辑联系,对于具体的问题,缺乏整体理解,致使所学知识支离破碎．问题的产生,除了与学生逻辑思维水平有关外,同样也与教师的教学有很大联系．

三、问题解决的多角度探究

受思维定势的影响,学生解决问题时只考虑用基本不等式来解,没有思考其他的方法．关于求最值范围问题,我们常用的方法:一是从函数的角度，利用函数的单调性、三角函数的有界性,利用导数;二是从不等式的角度，利用基本不等式、线性规划(数形结合);三是从方程的角度，方程根的分布、判别式等等．抓住方程、不等式、函数之间的内在联系,借助于具体的问题,形成知识组块．这种知识组块是镶嵌在解题认知结构上的明珠,是解题系统得以有效运作的枢纽.积累得越多、质量越高,那么解题者的解题能力就越强．这样,以最值范围为中心而组织起来的解题知识组块,还可以从以下角度思考:

解法2 (线性规划法)

我们知道二元二次方程4x2+y2+xy=1表示曲线,

若令w=2x+y(表示直线),则问题转换为,在4x2+y2+xy=1条件下,求w=2x+y的最值.想到线性规划,将问题转化为曲线4x2+y2+xy=1与直线y=-2x+w相切时有最值(因为x,y是实数)(如图1)，从而通过联立方程组由Δ≥0,求出w的范围．

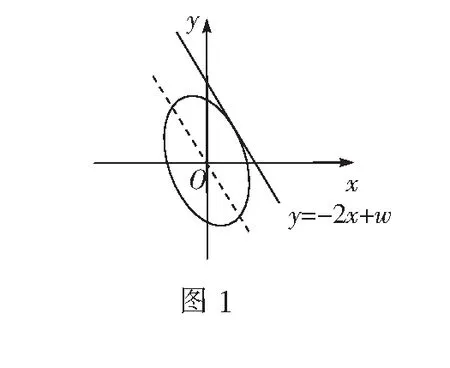
解法3 (判别式法)

与线性规划法相比较,考虑问题的角度不同,但本质上是一样的．令w=2x+y,则y=-2x+w，代入方程4x2+y2+xy=1,整理得到关于x的方程6x2-3wx+w2-1=0,由方程有根,Δ≥0,求出w的范围．

解法4 (三角换元)

由条件4x2+y2+xy=1,配方可以得到

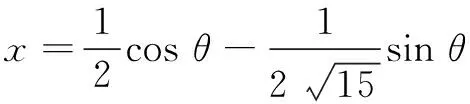
四、问题的变式探究

变式1 已知x>0,y>0,若4x2+y2+xy=1,求2x+y的最大值.

评注 条件变为x>0,y>0,利用基本不等式法是最简单的．若用线性规划法,此时二元二次方程表示的不是完整的曲线,相切能不能达到还有待进一步验证;若用判别式法,此时应考虑方程有正根的情况;若用三角换元,要考虑θ的范围问题．

变式2 已知x>0,y>0,若4x2+xy=1,求2x+y的范围.

评注 此时条件和结论之间无法匹配,基本不等式用不上．其他的三种方法可以解决,但是要结合x>0,y>0,解答的过程稍显复杂．注意到条件是二元二次方程,要求一个二元函数的最值问题,通常还有一个途径,就是消元,转化为一元函数的最值问题,再用单调性或基本不等式求解．

变式3 已知x>0,y>0,若2x+y+xy=1,求2x+y与xy的最小值．

在课堂教学中,一题多解、变式训练是常见的教学方式．教师在课堂设计时要充分发挥每道题的教育功能,深刻挖掘问题的内涵,激发学生的学习兴趣,使不同层次的学生都能够利用自己所掌握的数学知识解决问题,并逐步培养起学生主动探究的精神和创新意识．真正能够衡量和甄别学生数学能力和水平的不是对他们对静态知识的记忆、再现和简单应用,而是他们从数学活动中获得的知识出发,对静态结果知识所进行的动态理解、阐释、批判、综合和创新．

教师要能够通过一道题揭示和建立新旧知识的联系,使学生弄清知识的基本结构．在习题讲评课时不能就错论错、就题论题,而应站在更高的视角来审视问题,把题目中涉及到的基础知识和基本技能向广度和深度延伸、拓展,尽可能地构建知识间的广泛联系,从“点”出发,把“面”呈现给学生．同时通过开展一题多解、变式训练,将解决问题的相关知识进行整合,以重组和优化学生的认知结构．无结构的知识是散乱的,提取时不容易,有结构的知识则是彼此联系着的,便于记忆和迁移．