固体颗粒对直齿轮瞬态热弹流润滑的影响
2016-12-17黄兴保王优强
黄兴保, 王优强, 刘 前, 董 宁
(青岛理工大学 机械工程学院,山东 青岛 266033)
固体颗粒对直齿轮瞬态热弹流润滑的影响
黄兴保, 王优强, 刘 前, 董 宁
(青岛理工大学 机械工程学院,山东 青岛 266033)
文章建立了含有固体颗粒的直齿轮弹流润滑模型,推导了Reynolds方程,考虑了时变效应和热效应,分析了固体颗粒的形状尺寸和速度对油膜压力、膜厚以及温度的影响。结果表明:考虑固体颗粒后,颗粒所在区域的油膜压力变大,膜厚变小;移动的颗粒能够小幅度增大膜厚,但速度过大则膜厚减小;固体颗粒形状越接近球形时,油膜压力增幅变大,膜厚变小,颗粒越扁长时,油膜压力增幅变小,膜厚变大;考虑颗粒后的最小膜厚变小,最大温度升高明显;在颗粒位置处,油膜温度明显升高,静止颗粒引起的温升最小,且随着颗粒速度的增大,颗粒所在区域的最大温升位置右移,整体温度分布也随着颗粒速度的增大而变化。
固体颗粒;直齿轮;弹流润滑;时变效应;热效应
齿轮传动广泛应用于航空、航海等领域,尤其是大型机器设备的工作动力主要由齿轮提供,因此研究齿轮的弹流润滑具有重要意义。近年来,国内外关于弹流润滑的研究较多。文献[1]解决了高滑滚比条件下线接触热弹流润滑的数值解算难题;文献[2]建立了直齿轮瞬态混合润滑模型;文献[3]建立了线接触混合润滑模型,研究了混合润滑中滑动磨损的影响机制。目前关于考虑固体颗粒的研究可分为单个颗粒和颗粒流2个方向。关于单个颗粒的润滑,文献[4]研究了点接触弹流中固体颗粒对压力和膜厚的影响,但没有考虑颗粒对温度的影响;文献[5]分析了固液混合流体和表面形貌对压力和温度的影响,但没有分析固体颗粒对膜厚的影响;文献[6]研究了软颗粒变形对线接触EHD的影响,分析了软颗粒变形内部产热对油膜温度的影响,但没有考虑不同形状运动颗粒的影响。
关于颗粒流的研究也不少。文献[7]通过实验制备了MnZnFe2O4纳米磁性颗粒,从润滑油添加剂角度分析了MnZnFe2O4纳米磁性颗粒对纳米级油膜特性和成膜机理的影响,但没有分析微米级固体颗粒的运动对温度的影响;文献[8]从实验角度研究了颗粒流润滑过程中粉末层的微观破坏形式和机理,但没有探究运动颗粒对线接触EHL的影响;文献[9]研究了润滑过程中固体颗粒对低黏度润滑介质和固体颗粒含量对低黏度介质润滑特性的影响,但没有研究颗粒对压力、膜厚和温度的影响;文献[10]建立了含固体颗粒的脂润滑线接触弹流润滑模型,修正了脂润滑方程,分析了不同形状颗粒的尺寸、位置和速度对油膜压力和膜厚的影响,但没有考虑运动颗粒对温度的影响。
直齿轮弹流润滑属于无限长线接触问题,本文将考虑固体颗粒效应,修正Reynolds方程,考虑时变效应和热效应,深入分析颗粒的形状尺寸和运动速度对直齿轮润滑的影响
1 数学模型
1.1 考虑固体颗粒的Reynolds方程
含有固体颗粒的接触区弹流模型如图1所示。
(1) 区域1和区域3的润滑方程。推导过程详见流体润滑数值分析[11],整理后得到等温无颗粒的无限长线接触Reynolds方程为:
(1)
其中,p为曲膜压力;h为曲膜厚度;ρ为润滑密度;η为流体黏度;u为卷吸速度。
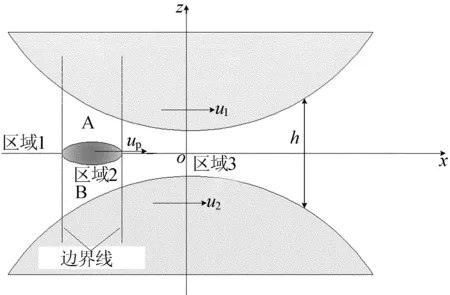
图1 含有固体颗粒的接触区弹流模型
(2) 区域2的润滑方程。区域2由A和B组成(图1),固体颗粒在z轴方向上的尺寸半长记为z0,颗粒上表面任一点的z坐标记为zp,颗粒速度为up,推导过程参考文献[11]。整理后得到等温条件下考虑固体颗粒的Reynolds方程为:
(2)
1.2 基本方程
1.2.1 Reynolds方程
考虑热效应的区域1和区域3的Reynolds方程[11]为:
(3)
考虑热效应的区域2 Reynolds方程[11]为:
(4)
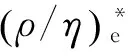
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
Reynolds方程的边界条件为:
(13)
1.2.2 膜厚方程
膜厚方程为:
(14)
1.2.3 载荷方程
在每一瞬时,油膜压力的合力必须与瞬时载荷相平衡,则有:
(15)
1.2.4 润滑油温度控制方程——能量方程
润滑油温度控制方程——能量方程[12]为:
(16)
其中,T为油膜温度;cp为流体的等压比热,对于润滑油而言,其等压比热与等容比热相差甚微,所以可以笼统地统一写成c;k为流体的热传导系数,对于润滑油,c和k均可认为是常数。能量方程(16)由4部分组成,其物理意义从左到右分别为对流换热项、热传导项、压力功项和热耗散项。
方程(16)的温度边界条件为T=T0(在u(xin,z,t)≥0及u(xout,z,t)≤0处)。
1.2.5 固体能量方程
对于时变问题,可以通过把运动的固体轮齿设想为流体的方法,经简化流体的能量方程而得到轮齿1和轮齿2的固体能量方程[12](即热传导方程),即
(17)
其中,c1和c2、ρ1和ρ2、k1和k2分别为轮齿材料1和2的比热、密度、热传导系数。在弹流理论中计算弹性变形和进行热分析时,可以把轮齿材料作为空间半无限体看待,因此轮齿材料内的空间坐标z1、z2的指向均是向上的,即与油膜中z坐标的指向相同。
1.2.6 黏度方程
润滑剂的黏度为压力和温度的函数,选用Roelands黏压黏温关系,即
(18)
其中
A3=1/(T0-138),A4=138/(T0-138),
其中,α为黏压系数;β为黏温系数。
1.2.7 密度方程
润滑剂的密度也是压力和温度的函数,本文采用Dowson-Higginson密压密温关系,即
(19)
其中,C1=0.6×10-9Pa-1;C2=1.7×10-9Pa-1;
C3=6.5×10-4K-1。
2 方程的无量纲化
为了方便求解,需要对所建立的数学模型无量纲化。无量纲化参量定义如下:
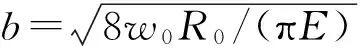
为保证润滑状态为富油状态,x方向通常取边界坐标为xin=-4.6b,xout=1.4b,b为初始载荷w0作用下的Hertz接触区半宽。
3 数值方法
压力计算采用考虑温度影响的多重网格法,膜厚计算使用多重网格积分法,温度计算采用逐列扫描技术。将齿轮的1个轮齿从啮入点到啮出点沿啮合线的全过程作为1个计算周期,把该计算周期分为Nt个瞬时进行计算。在每个瞬时,求解瞬态热弹流的过程均包括压力和温度的分别求解,压力和温度求解需交替进行。在压力计算子过程中假定温度场已知,通过解Reynolds方程求压力,应用该压力求膜厚,并调整刚体中心膜厚使压力满足载荷平衡方程。温度计算子过程中假定压力和膜厚已知,通过解油膜的能量方程和两轮齿固体的热传导方程得到温度场分布。
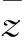
4 结果分析与讨论
载荷沿啮合线的变化如图2所示,tA、tB、tC、tD、tE为载荷时变的5个瞬时。其中,横坐标s为啮合点距固定节点的距离;纵坐标为无量纲载荷W。
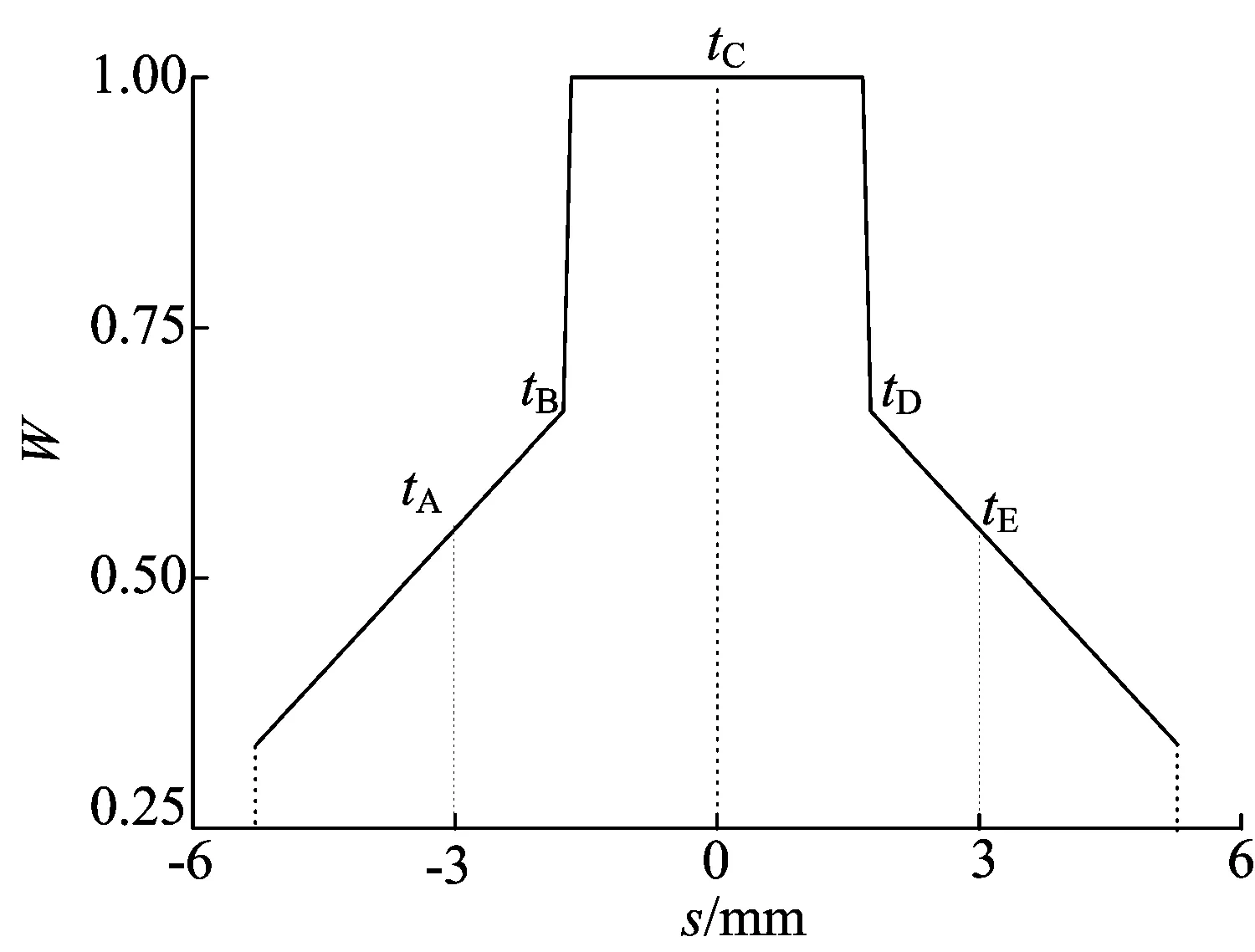
图2 载荷沿啮合线的变化
润滑相关参数见表1所列。

表1 润滑相关参数
4.1 有、无固体颗粒对齿轮润滑的影响
本文以一般椭球形固体颗粒作为分析模型。有、无固体颗粒的压力和膜厚对比如图3所示。其中,横坐标为接触区跨度,用无量纲X表示(下文同)。由图3可以看出,加入颗粒的区域2的油膜压力与无颗粒情况相比显著增大,由区域2向区域3过渡时压力减小,区域3的压力变化趋势与无颗粒情况大致相同,且略小于无颗粒情况的油膜压力。由图3还可以看出,从入口到出口的润滑油经过颗粒后膜厚明显减小,随后一直小于无颗粒情况的膜厚,且油膜颈缩处的膜厚也减小了。
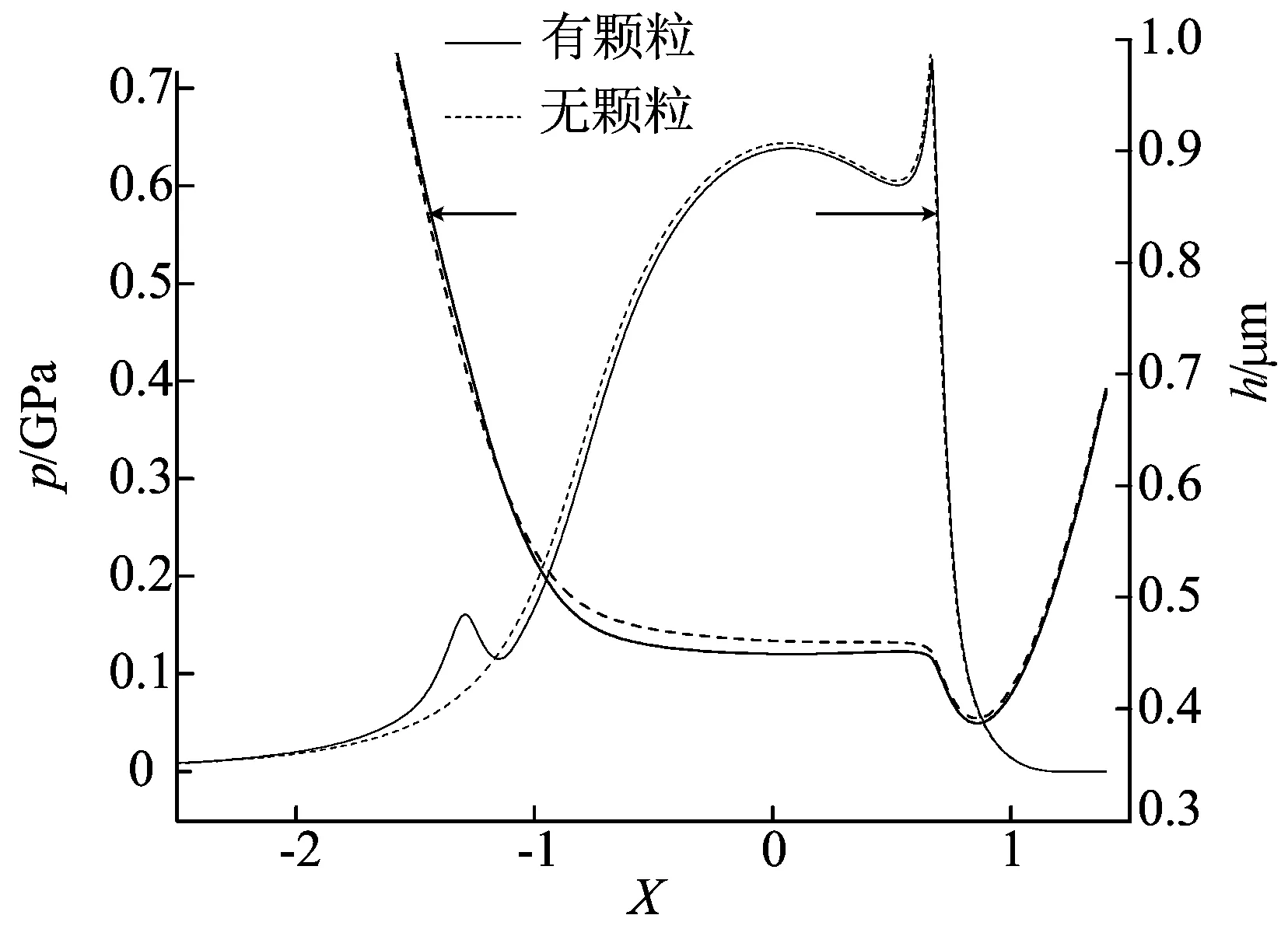
图3 有、无固体颗粒的压力和膜厚对比
4.2 不同速度的固体颗粒对齿轮润滑的影响
颗粒速度对压力和膜厚的影响如图4所示。图4a和图4b分别为不同颗粒速度下的压力和膜厚图(颗粒中心位置xC=-1.3,椭球形颗粒无量纲长半轴a=0.2,短半轴b=0.15)。
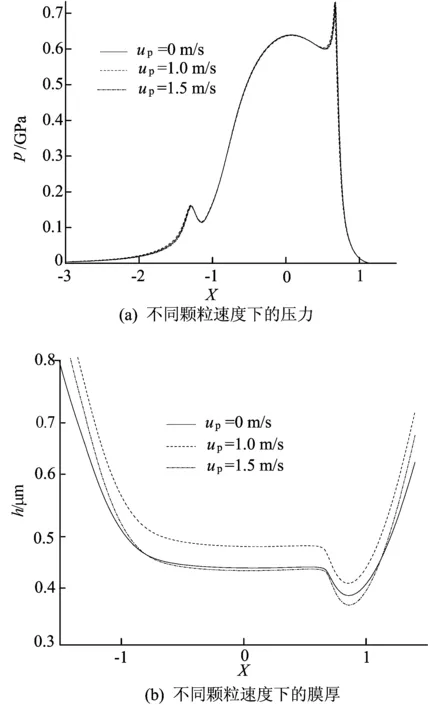
图4 不同颗粒速度对压力和膜厚的影响
由图4可知,固体颗粒速度对油膜压力几乎没有影响,但是固体颗粒速度对膜厚影响显著。当up=1.0 m/s时膜厚增大,且从颗粒位置到出口处膜厚均大于up=0时的膜厚;当up=1.5 m/s时,膜厚比up=0时的有所减小,且从颗粒位置到出口处均小于up=0时的膜厚。由此可推断合适速度的颗粒会增大润滑油膜厚,但速度过大会使膜厚减小。
4.3 不同形状尺寸颗粒对齿轮润滑的影响
本文考虑的固体颗粒为椭球体颗粒,其形状和尺寸主要由椭球的长短轴之比决定,因为研究的是直齿轮弹流润滑,属于无限长线接触问题,所以只需考虑x和z轴方向的尺寸,因此颗粒的形状尺寸主要由椭圆长短轴之比a/b决定。颗粒形状对压力和膜厚的影响如图5所示。图5a和图5b分别为不同a/b值下的压力和膜厚图(up=0,XC=-1.3)。
由图5a可知,a/b值越小,油膜压力变化越大,a/b值越大,油膜压力变化越小,当a/b值足够大时,颗粒对油膜压力的影响几乎可以忽略,也就是说片状颗粒对压力的影响很小;由图5b可知,颗粒形状尺寸对膜厚有影响,且a/b值越大,膜厚越大,a/b值越小,膜厚越小。
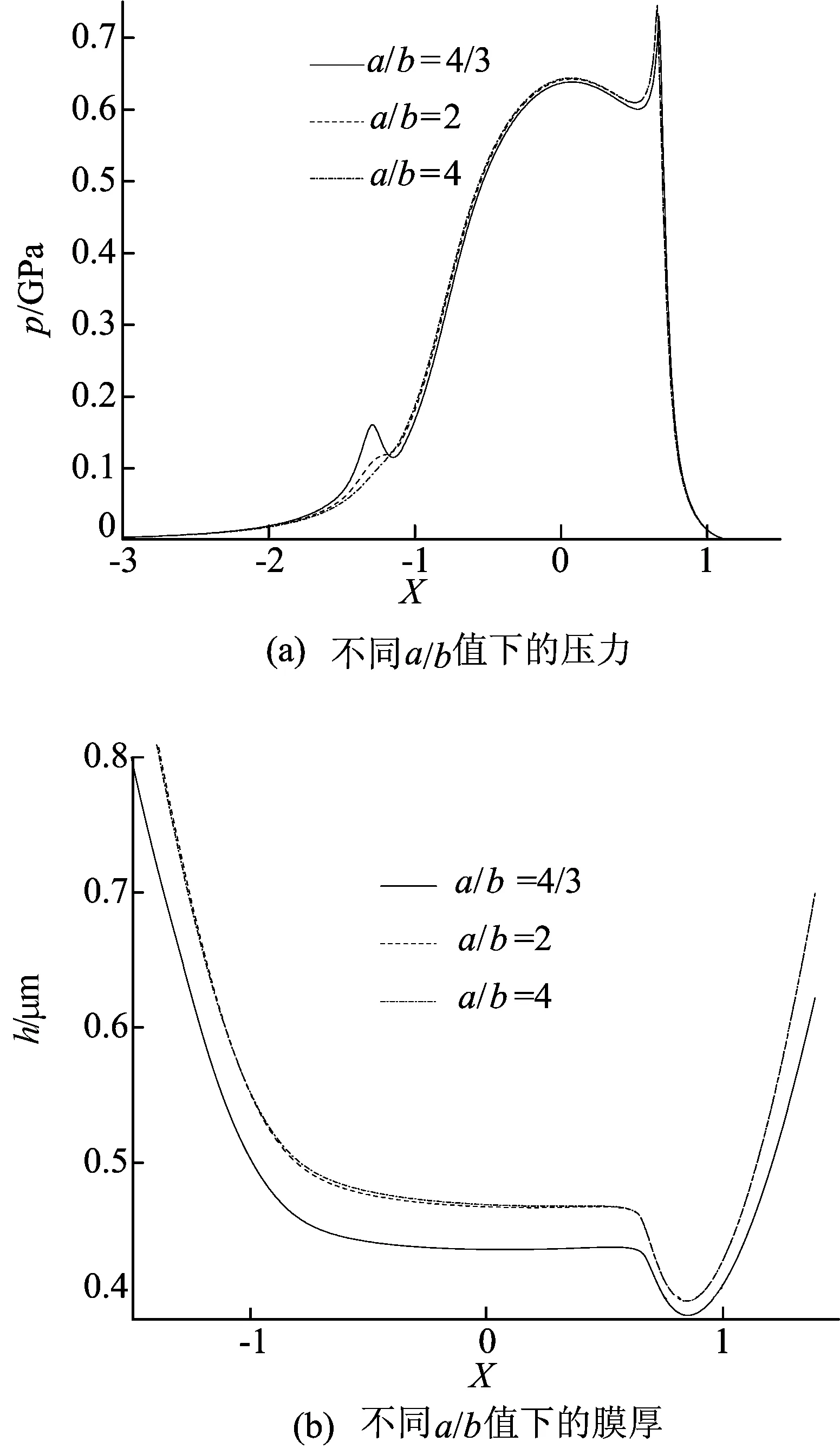
图5 颗粒形状对压力和膜厚的影响
4.4 颗粒对最小膜厚和最大温度的影响
有、无颗粒条件下的最小膜厚和最大温度分布如图6所示。
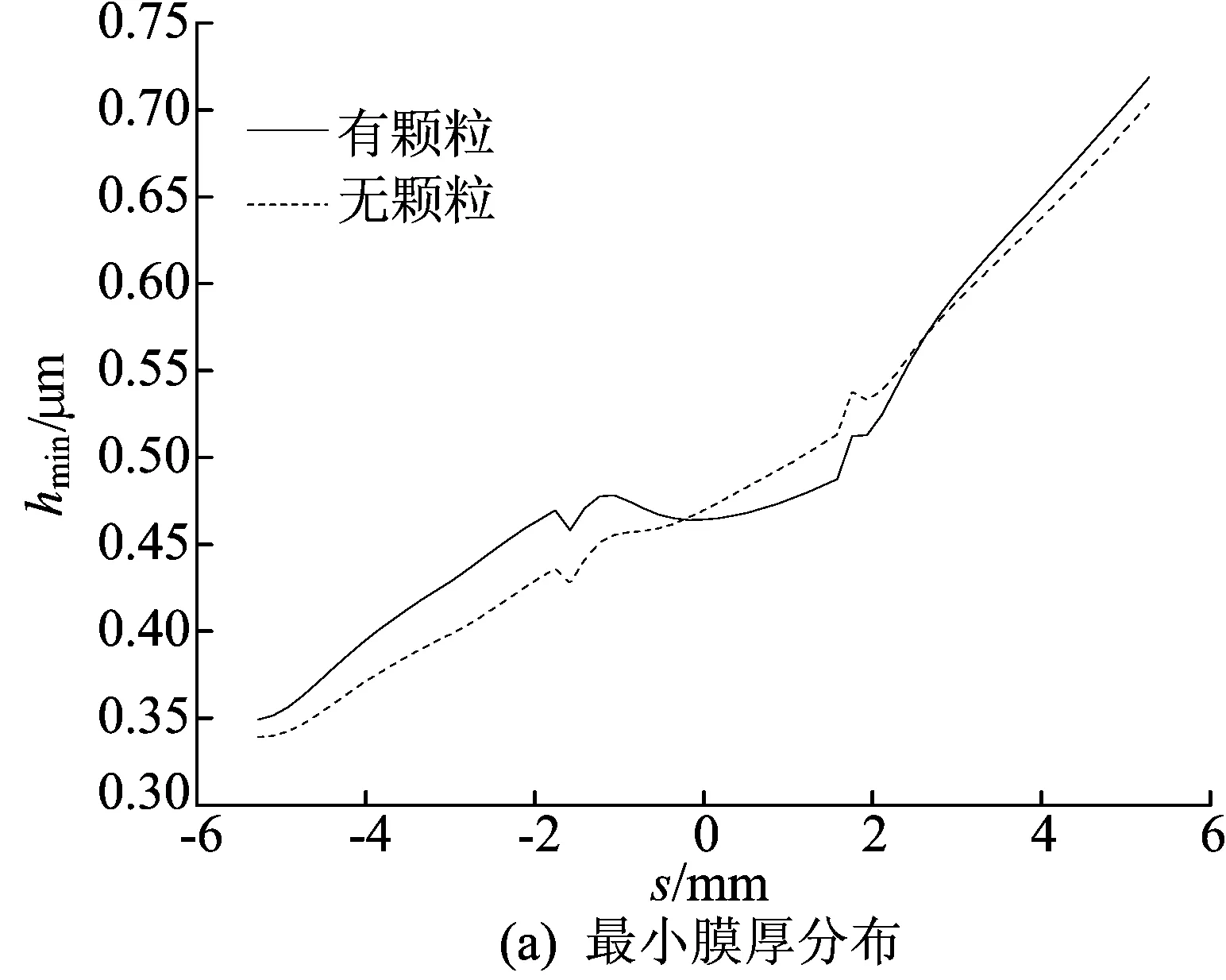
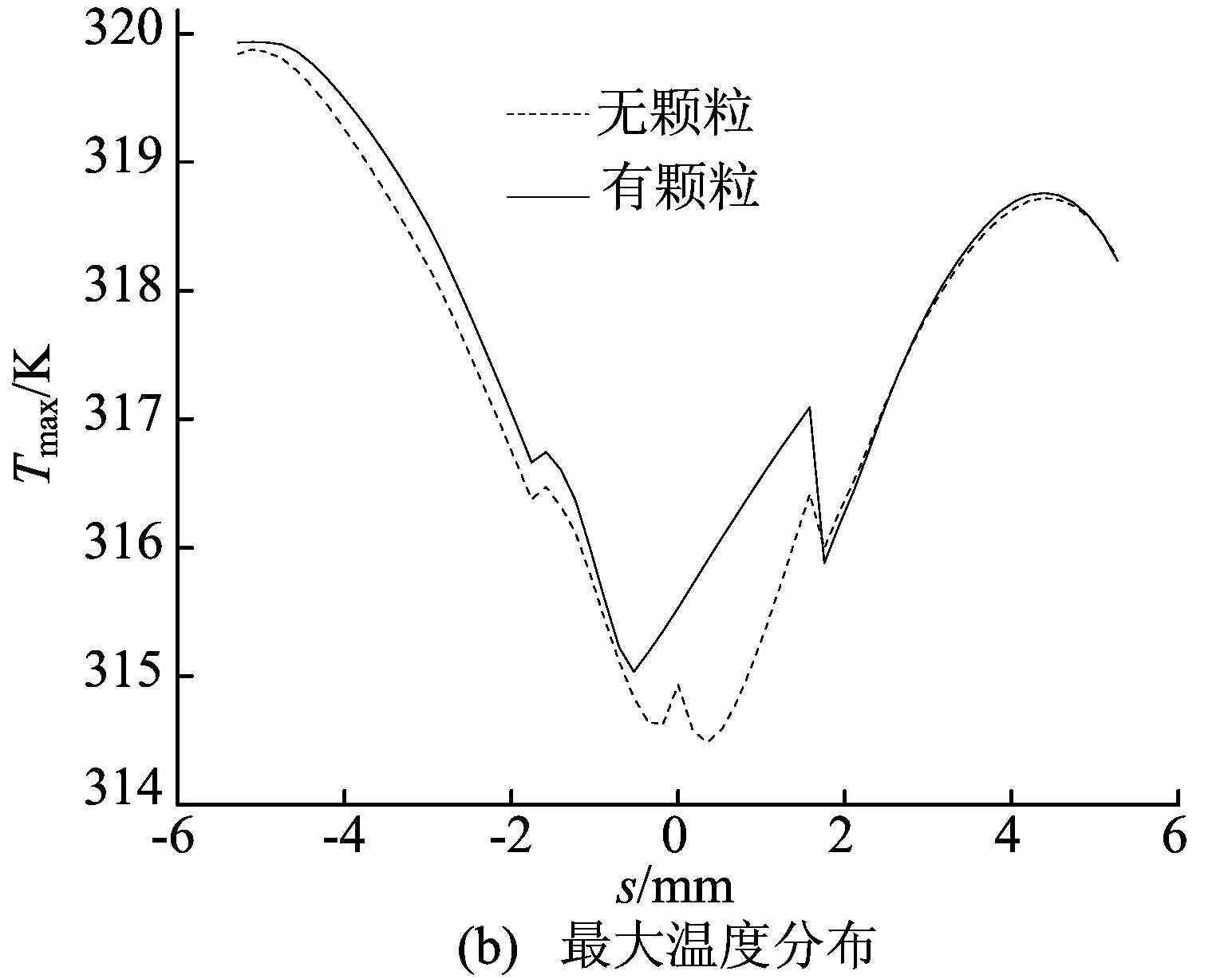
图6 最小膜厚和最大温度分布
从图6a可以看出,润滑油经过颗粒所在区域2后最小膜厚有所减小;由图6b可知,加入颗粒后的最大温度有所升高,润滑油经过颗粒所在区域2后温度明显升高。
为验证数值算例的准确性与可靠性,下面根据Dowson在1967年修正的最小膜厚经验公式[11]进行验证。
最小膜厚经验公式的无量纲形式为:
最小膜厚经验公式的有量纲形式为:
图2中tA~tE5个瞬时对应的啮合点位置依次记为1、2、3、4、5,现根据上述最小膜厚经验公式分别计算这5个啮合点位置的最小膜厚值,然后与数值算例结果进行比较,比较结果与误差见表2所列。
由表2可以看出,5个啮合点处的最小膜厚数值算例结果和经验值的相对误差均在10%以内,说明本文的数值算例结果具有较好的准确性和可靠性。
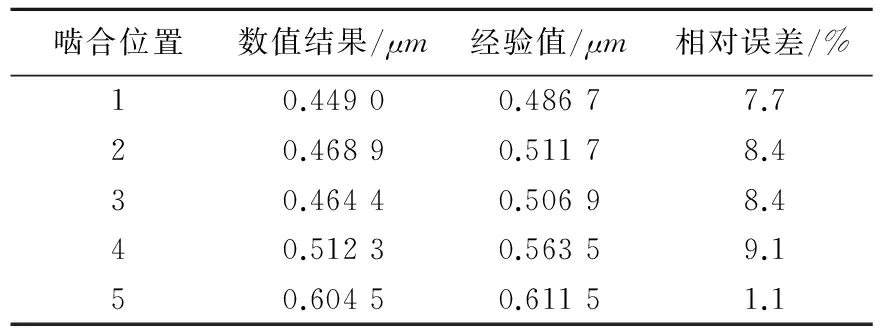
表2 最小膜厚数值结果和经验值的比较
4.5 时变对压力和膜厚的影响
瞬态压力和膜厚分布如图7所示。其中,tA、tB、tC、tD、tE分别为图2中对应的5个瞬时。由图7可知,时变效应对压力和膜厚的影响较大,压力变化明显;加入颗粒处压力增大,油膜颈缩位置向左或向右移动。
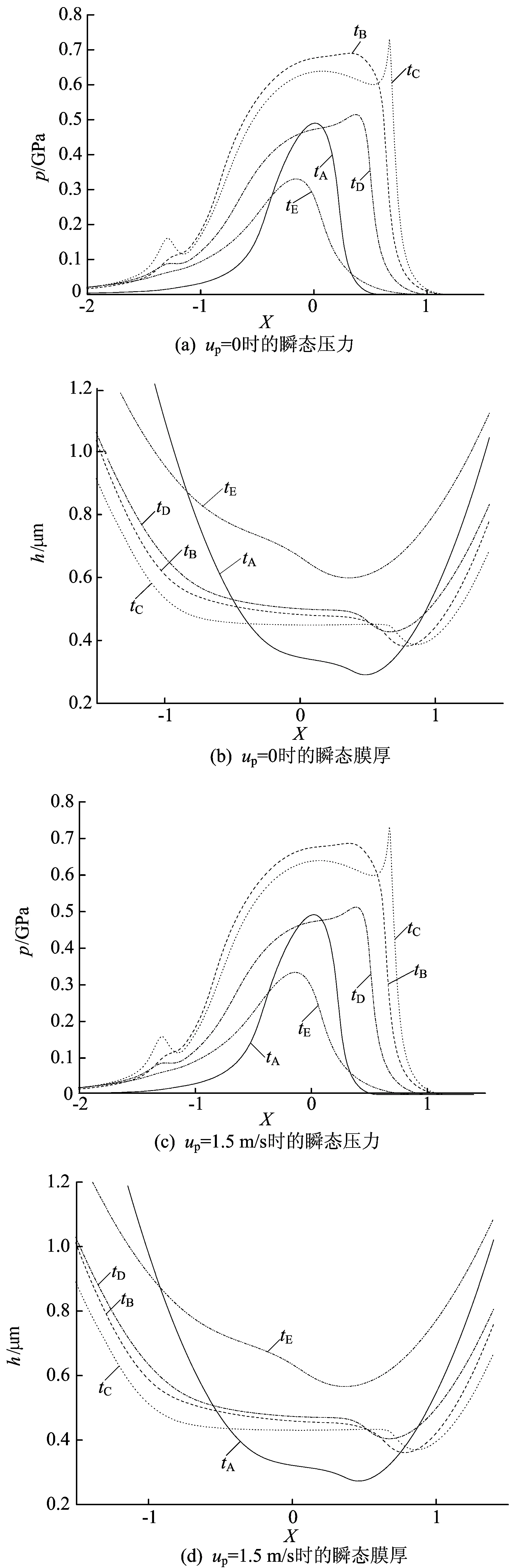
图7 瞬态压力和瞬态膜厚分布
4.6 不同速度的颗粒对温度的影响
不同速度颗粒下温度的分布如图8所示,其中,坐标均为无量纲参数。
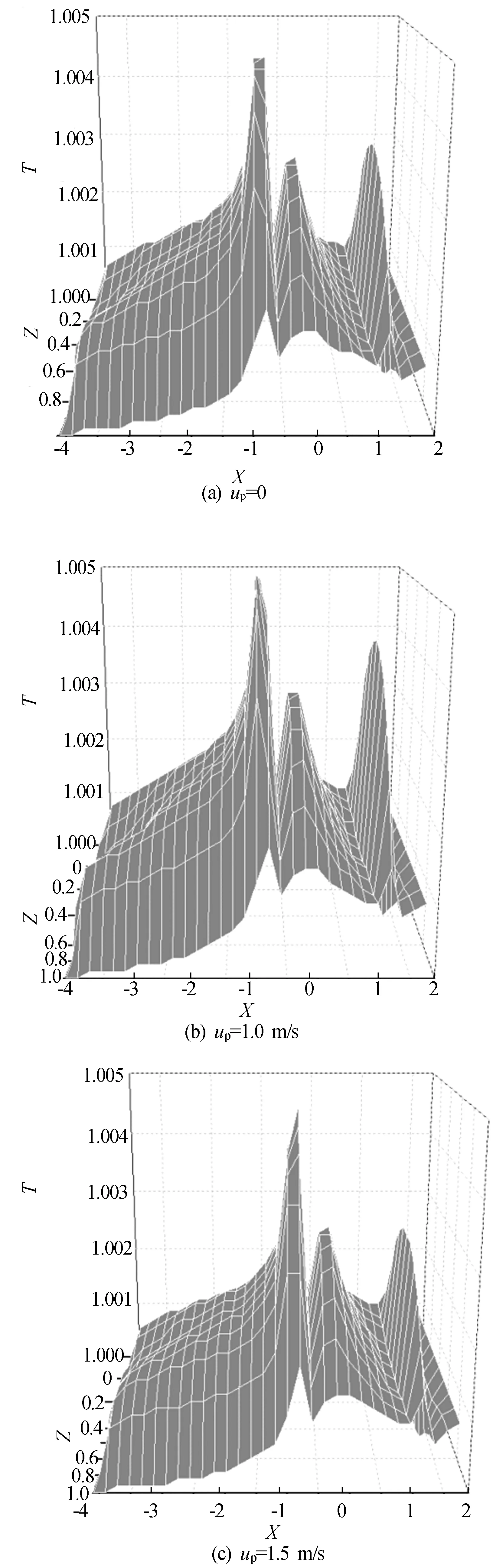
图8 不同速度颗粒下温度的分布
由图8可以看出,在加入颗粒位置处,油膜温度明显升高,甚至高于二次压力峰处的温度,故在实际齿轮跑合润滑时温度控制所参考的无颗粒情况下的温度分布偏小,容易导致润滑油温度过高而迅速失效,存在一定程度上的安全隐患;静止颗粒引起的温升最小,且随着up的增大,最大温升位置右移,整体温度分布也随着up的增大而变化,可见移动的颗粒对温度影响非常显著。因此,在齿轮跑合过程中需要实时监测润滑油中磨屑的含量,以便进行温度控制,从而保证跑合质量。
4.7 不同形状颗粒对温度的影响
不同椭圆长短轴之比a/b的温度分布三维图如图9所示。其中,坐标均为无量纲参数。
由图9可以看出,图9a中的颗粒所在区域的温升最大,图9c中的温升最小。由此可知,a/b值越小,颗粒所在区域的温升越大;a/b值越大,颗粒所在区域的温升逐渐减小;当a/b值足够大时,颗粒对区域2的温度几乎没有影响。而且不同的a/b值也影响出口处润滑油的温升,a/b值越小,出口处温升越小,a/b值越大,出口处温升越大。
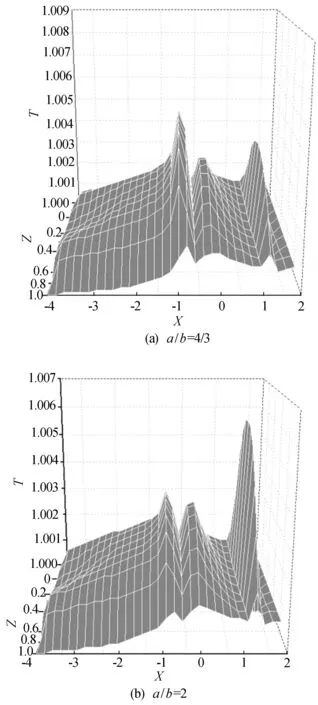
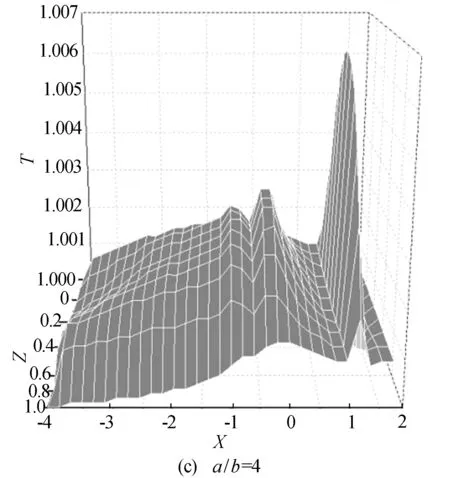
图9 不同形状颗粒的温度分布
5 结 论
(1) 考虑固体颗粒后,颗粒所在区域的油膜压力变大,膜厚变小。颗粒速度对压力几乎没影响,对膜厚有影响,移动的颗粒能够小幅度增大膜厚,但速度过大则膜厚减小。a/b值较小时,油膜压力增幅大,膜厚变小;a/b值较大时,油膜压力增幅小,膜厚变大。
(2) 加入颗粒后的最小膜厚变小,最大温度升高明显,故在进行齿轮跑合时要注意温度的控制,防止润滑油温度过高。压力和膜厚的时变效应显著,但颗粒速度对瞬态压力和膜厚分布影响不明显。
(3) 在颗粒位置处,油膜温度明显升高,甚至高于二次压力峰值处的温度,静止颗粒引起的温升最小,且随着up的增大,最大温升位置右移,整体温度分布也随着up的增大而变化。a/b值越小,颗粒所在区域的温升越大;a/b值越大,颗粒所在区域的温升逐渐减小;不同a/b值也影响出口处润滑油的温升,a/b值越小,出口处温升越小,相反,a/b值越大,出口处温升明显增大。
[1] YANG P R,Qu S Y,Chang Q Y,et al.On the theory of thermal elastohydrodynamic lubrication at high slide-roll ratios-line contact solution[J].Journal of Tribology,2001,123(1):36-41.
[2] LI S,KAHRAMAN A.A transient mixed elastohydrodynamic lubrication model for spur gear Pairs[J].Journal of Tribology,2009,132(1):011501-1-9.
[3] ZHU D,MARTINI A,WANG W Z,et al.Simulation of sliding wear in mixed lubrication[J].Journal of Tribology,2007,129(3):544-552.
[4] KANG Y S,SADEGHI F,Ai X L.Debris effects on EHL contact[J].Journal of Tribology,2000,122(4):711-720.
[5] WANG W,LIU K,JIAO M H.Thermal and non-Newtonian analysis on mixed liquid-solid lubrication[J].Tribology International,2007,40(7):1067-1074.
[6] NIKAS G K.An advanced model to study the possible thermomechanical damage of lubricated sliding-rolling line contacts from soft particles[J].Journal of Tribology,2000,123(4):828-841.
[7] 冯雪君,刘书进,晁宇.MnZnFe-2O-4纳米磁性颗粒对薄膜润滑性能的影响[J].机械工程学报,2011,47(7):116-122.
[8] 王伟,刘小君,刘焜.颗粒流润滑过程中粉末层的微观破坏形式和机理分析[J].摩擦学学报,2012,32(3):258-263.
[9] 董岑华,韩会军,段诚,等.固体颗粒对低黏度介质润滑特性的影响[J].润滑与密封,2011,36(2):4-8.
[10] 谢小鹏,彭朝林,陈树林.固体颗粒对脂润滑线接触弹流影响的数值分析[J].华南理工大学学报(自然科学版),2012,40(7):51-56.
[11] 杨沛然.流体润滑数值分析[M].北京:国防工业出版社,1998.
[12] 王优强,衣雪鹃,杨沛然.渐开线直齿轮瞬态微观热弹流润滑分析[J].机械工程学报,2007,43(11):142-148.
(责任编辑 胡亚敏)
Influence of solid particles on transient thermal elastohydrodynamic lubrication of spur gears
HUANG Xingbao, WANG Youqiang, LIU Qian, DONG Ning
(School of Mechanical Engineering, Qingdao Technological University, Qingdao 266033, China)
The elastohydrodynamic lubrication model of spur gears containing solid particles was set up. The Reynolds equation considering solid particles was deduced. Taking the time-variant effect and thermal effect into account, the influence of shape size and speed of solid particle on the oil film pressure, film thickness and temperature was investigated. The results show that considering solid particle, the oil film pressure increases and the film thickness decreases in the region where debris settles. Moving particle makes contribution to the increase of film thickness to a small extent, but if the speed of particle is too high, the film thickness may diminish. When the solid particle is more spherical, the oil film pressure increases and the film thickness decreases. When the solid particle is more prolate, the oil film pressure decreases and the film thickness increases. The minimum film thickness decreases and the maximum temperature increases significantly when considering the effect of solid particle. The oil film temperature increases evidently in the region where debris settles. The temperature rise caused by stationary particle is the minimum. The position of maximum temperature rise moves right with the increase of particle speed. The overall temperature distribution also varies with the increase of particle speed.
solid particle; spur gear; elastohydrodynamic lubrication; time-variant effect; thermal effect
2015-05-12;
2016-06-29
国家自然科学基金资助项目(51175275);青岛市科技计划资助项目(12-1-4-4-(2)-JCH)
黄兴保(1990-),男,安徽怀宁人,青岛理工大学硕士生; 王优强(1970-),男,山东沂水人,博士,青岛理工大学教授,博士生导师.
10.3969/j.issn.1003-5060.2016.11.004
TH117.2
A
1003-5060(2016)11-1456-08
