表面粗糙度对接触界面间流体流动的影响

李 皓, 刘小君, 张 彤, 刘 焜

(合肥工业大学 机械与汽车工程学院, 安徽 合肥 230009)



表面粗糙度对接触界面间流体流动的影响

李 皓, 刘小君, 张 彤, 刘 焜

(合肥工业大学 机械与汽车工程学院, 安徽 合肥 230009)

文章建立了粗糙接触界面间流动分析模型,研究了黏性流体在压力驱动状态下的流动特性。该模型将界面简化为两平板,用规则微凸体模拟表面粗糙度;定义了面积比、相对粗糙度2个物理量,并分析了它们对流动的速度、压强、壁面切应力的影响。结果表明,界面间层流阻力增加的来源是微凸体附近回流带来的较大压差阻力，用微凸体模拟粗糙度可简化实际复杂表面,通过改变微凸体的结构和分布可以分析工程中接触界面间的流动问题。

接触界面;微凸体;面积比;相对粗糙度;回流

0 引 言

液体在接触界面流动时,由于界面间隙处于微米量级,该流动属于微尺度流动。随着20世纪80年代后微机电系统(micro-electro-mechanical system,MEMS)的出现以及近来芯片设计制造的发展,微尺度流动得到了广泛关注。

随着特征尺度的减小,在宏观流动中往往被忽略的表面粗糙度已经达到了与特征尺度相同的量级,这时表面粗糙度对流动的影响便不容忽略。表面粗糙度对微尺度通道中液体流动的影响显著,是造成与很多流动阻力研究结果相悖的原因之一。目前关于微管道内流动特性的研究,不同研究者得到的实验结果差异很大。文献[1]指出,在层流状态下,3%～7%的相对粗糙度可以导致微管道内流动阻力的明显增加;而文献[2]表明,具有适当粗糙微结构的超疏水表面会出现滑移,从而降低流动阻力。可见粗糙度对于微通道流动的影响还需要更深入的研究。

由于实验的不确定性,文献[3]采用数值模拟方法研究流动问题。为了研究粗糙度对微通道流动的影响,文献[4]使用等距正方形微凸体形成不规则粗糙微通道,并使用“熵增”为参数显示粗糙度引起的流动阻力增量;文献[5]采用分子动力学与有限容积法多尺度耦合算法对粗糙微通道内的液体Poiseuille流动进行了模拟,分析了微凸体高度、分布以及几何形状对通道内流动速度和边界滑移长度的影响;文献[6]以三角形锯齿状微凸体模拟固体表面的粗糙度,采用计算流体力学(computational fluid dynamics,CFD)流固共轭传热数值研究了粗糙元间距对平行平板微通道流动的影响。结果表明，随着粗糙元间距的增大,阻力逐渐下降。

目前，关于表面粗糙度影响微尺度流动的研究逐渐扩展到与工程应用相关的试验探索和验证上,虽然研究方法各不相同,但数值模拟已经成为一种公认的重要研究手段。然而,大部分学者研究的是微管道内的流体流动状态,对于确定的微管道,其管径是定值,而实际接触界面的间隙却随工况条件而变化。因此,本文引入相对粗糙度来描述界面间隙的变化。微凸体均布在光滑平板上,上、下2块平板对称布置，把表面粗糙度简化为上、下底不同的梯形微凸体。该模型通过改变微凸体的结构和分布来模拟工程实际接触界面,用于开展界面间流动等研究。

1 数学模型

本文粗糙接触界面间流动分析模型的结构如图1所示。

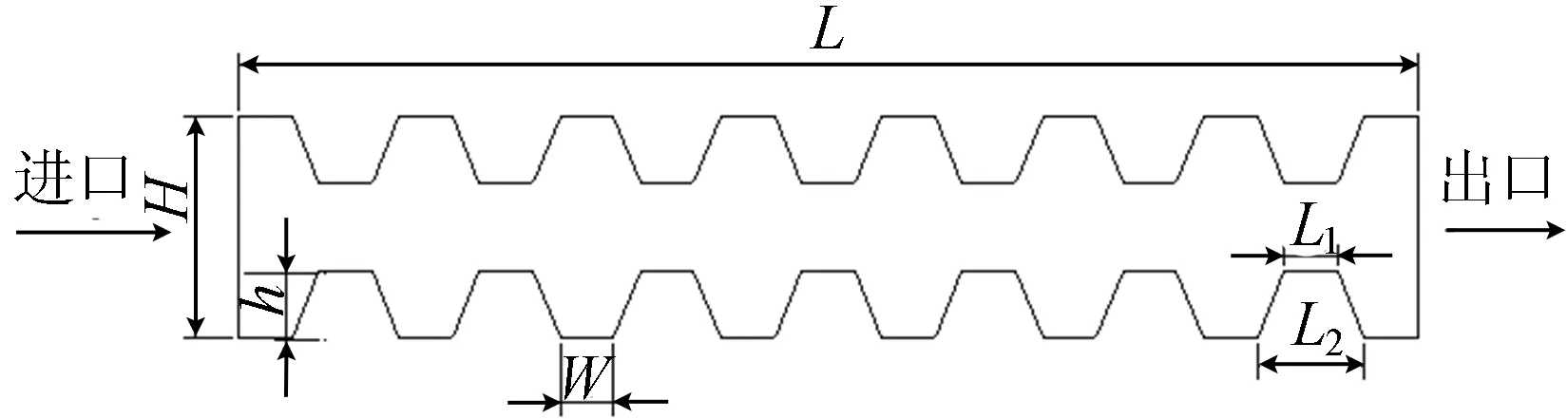
图1 模型结构

两平行平板间距H=20 μm,长度为L,宽度B=1 mm,平板的宽度远远大于它的高度,所以侧壁对整个流场的影响忽略不计。微凸体在光滑平板上均匀分布,微凸体间隔W=5 μm。设平板左右两端存在压力差p,在压力作用下,不可压缩黏性流体从左端流入,右端流出。

微凸体是由一系列上底可变的梯形组成。梯形微凸体上底长度为L1,下底长度为L2,高度为h,其中L2=10 μm,L1、h为变量。为了考虑不同微凸体的结构变化,定义面积比ε为:

(1)

面积比ε是梯形上下底长度之比,表示微凸体所占据面积的大小。当ε=0时,微凸体为三角形,所占据面积最小;当ε=1时,微凸体为矩形,所占据面积最大;ε在0～1之间变动时,微凸体为等腰梯形。面积比ε是一个无量纲参数,代表着不同微凸体的结构。为了同时考虑表面粗糙度和界面间隙的耦合影响,引入相对粗糙度σ,即

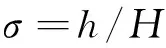
(2)

相对粗糙度σ也是一个无量纲参数,是微凸体高度与平板间距的比值,它反映了平板的粗糙程度,也从另一方面描述了界面间隙的变化。σ越大,表面就越粗糙;σ=0时,平板光滑。为了简化模型,微凸体高度h分别取2、4、6、8 μm,对应的σ取值分别为0.1、0.2、0.3、0.4。面积比ε和相对粗糙度σ分别从微凸体结构和表面粗糙程度来描述微凸体。

2 数值计算

2.1 计算方程

不可压缩黏性流体充满两平板之间区域,在压力驱动下流动。文献[1]通过实验发现,对于黏性流体在界面间的流动,连续性是可接受的,传统的流体力学方程组可以使用。对该流场列方程如下:

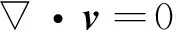
(3)

(4)

其中,v为流体速度；μ为流体动力黏度;ρ为流体密度。方程(3)为连续性方程,是质量守恒原理在流体运动中的表现形式。方程(4)为Navier-Stokes方程,是流体的运动方程式。

2.2 求解方法

采用基于有限体积法的流体计算软件Fluent对流场流力状态进行计算。考虑到流体流动的入口效应和边界层效应,在入口段和边界层进行了局部网格加密。计算过程中选择润滑油密度ρ=840 kg/m3,动力黏度μ=0.064 Pa·s;模型求解器选择压力基、显示、定常流;设置入口边界的压力为16 kPa,出口边界的压力为0;求解方程离散化时,设置压力计算方法为二级收敛,动量计算方法为二级向上收敛;控制残差在0～10-5范围内，其他保持Fluent默认设置。

2.3 网格无关性与算法验证

品质得分在54.70以上的为优质一级烤鸭，市售优质烤鸭中检测到的9种杂环胺总含量水平为5 757.02～6 859.31ng·g-1。

以ε=0.5、σ=0.3、高度为6 μm的梯形微凸体为例,进行网格无关性验证。为了考查微凸体的影响,把网格精度在x、y方向均提高1倍。计算结果显示,2套网格在Re数结果上相差1.5%。故选用第1套网格精度即可。第1套网格的示意图如图2所示。

图2 网格示意图(ε=0.5,σ=0.3)

采用上述算法和网格精度,计算与图2模型同等尺寸下的光滑壁面通道,结果与常规尺度理论分析解吻合,速度符合抛物线规律,Re数偏差也在控制范围内。

3 计算结果与分析

3.1 速度分布

当σ=0.3时,出口截面上速度vout随平板间距变化的规律如图3所示。

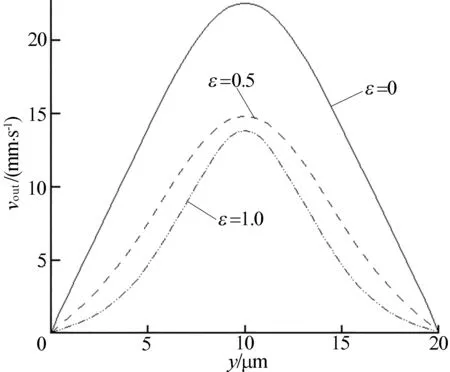
图3 出口截面速度分布

由图3可以看出，3条曲线都可以由抛物线来模拟,说明粗糙平行平板间的流动仍满足Poiseuille流运动规律。由于微凸体造成有效流通面积的减小,粗糙平板间速度数值明显减小,这说明流动是以小速度沿通道向前流动,流动过程中速度在不断下降。三角形微凸体对应的出口速度明显高于矩形和梯形,可见微凸体结构对流动的影响很大。随着ε的增大,微凸体占据的面积越大,速度急剧减小。

出口截面上的最大速度随ε、σ变化的规律如图4所示。因为出口截面上速度成抛物线规律(见图3),抛物线的顶点为出口的中点，所以最大速度出现在出口的中间位置。由图4可知，随着ε的增大,微凸体的上底长度不断增加,增大了流体与壁面的接触面积,同时,微凸体所占据的面积也不断增大,因此流体速度不断降低；σ的增大造成流体有效流通空间变小,速度也因此降低。综上可知,出口最大速度随着面积比、相对粗糙度的增大而减小。

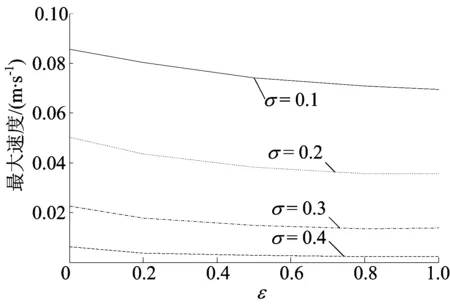
图4 出口截面最大速度随ε、σ变化的规律

3.2 压力分布

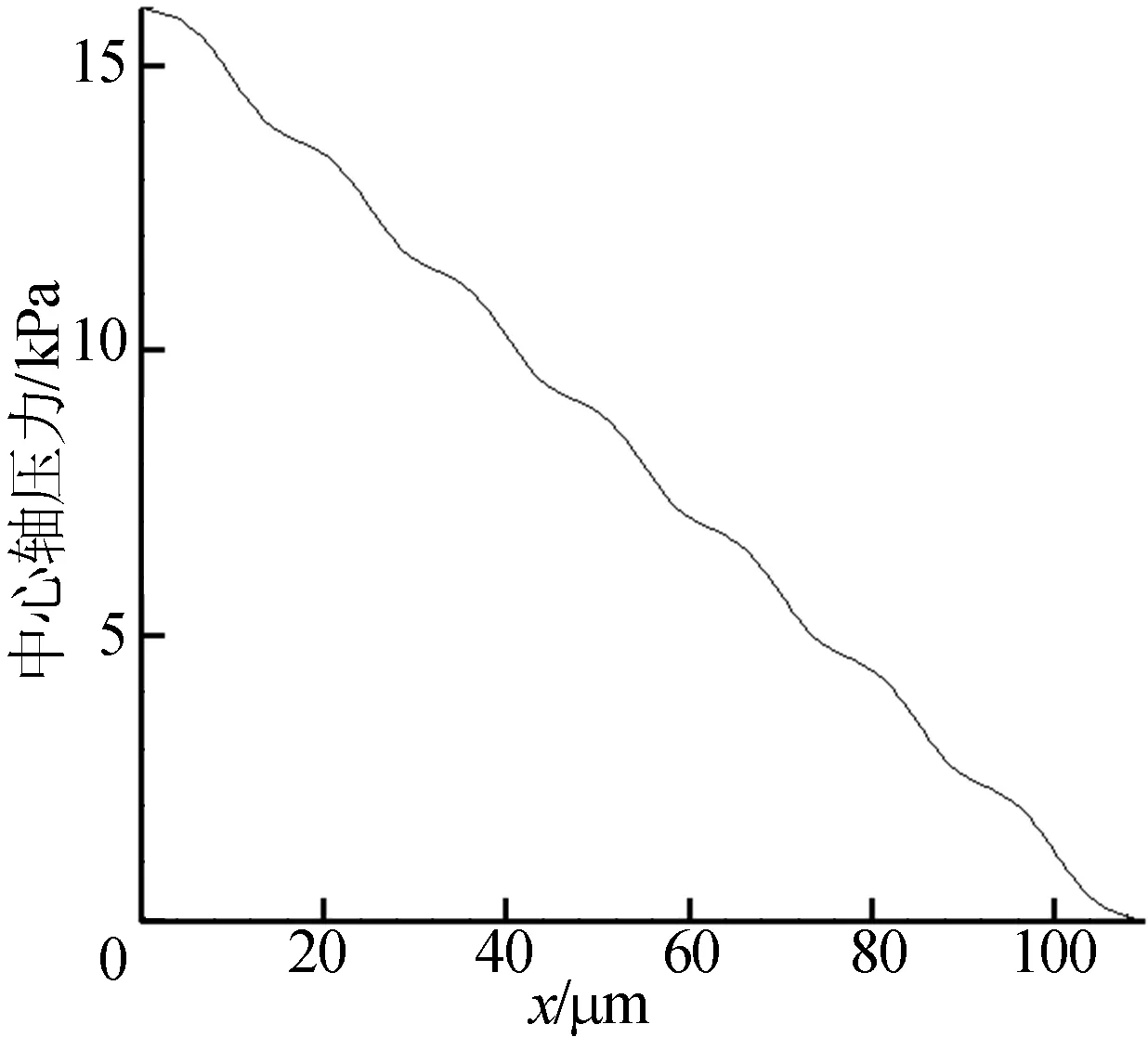
图5 界面中心轴压力(ε=0.5,σ=0.3)

对于粗糙度引起层流阻力增加的解释一直存在争议,例如，文献[7]认为表面粗糙度引起了壁面附近动量输运的增加,而文献[8]把粗糙度简化为管径的缩小。这2种说法都是从宏观角度给出的解释,本文则是从微凸体附近的流场结构来分析流动阻力增加的原因。

当ε=1、σ=0.2时,流场的速度矢量图如图6所示。由图6可以看出,微凸体附近流线发生变形,流体速度在微凸体前缘下降为0,形成停滞区,在微凸体后缘出现低速回流区。因此可以认为,微凸体前、后缘由于流动分离而产生的压差阻力造成了层流阻力的增加。

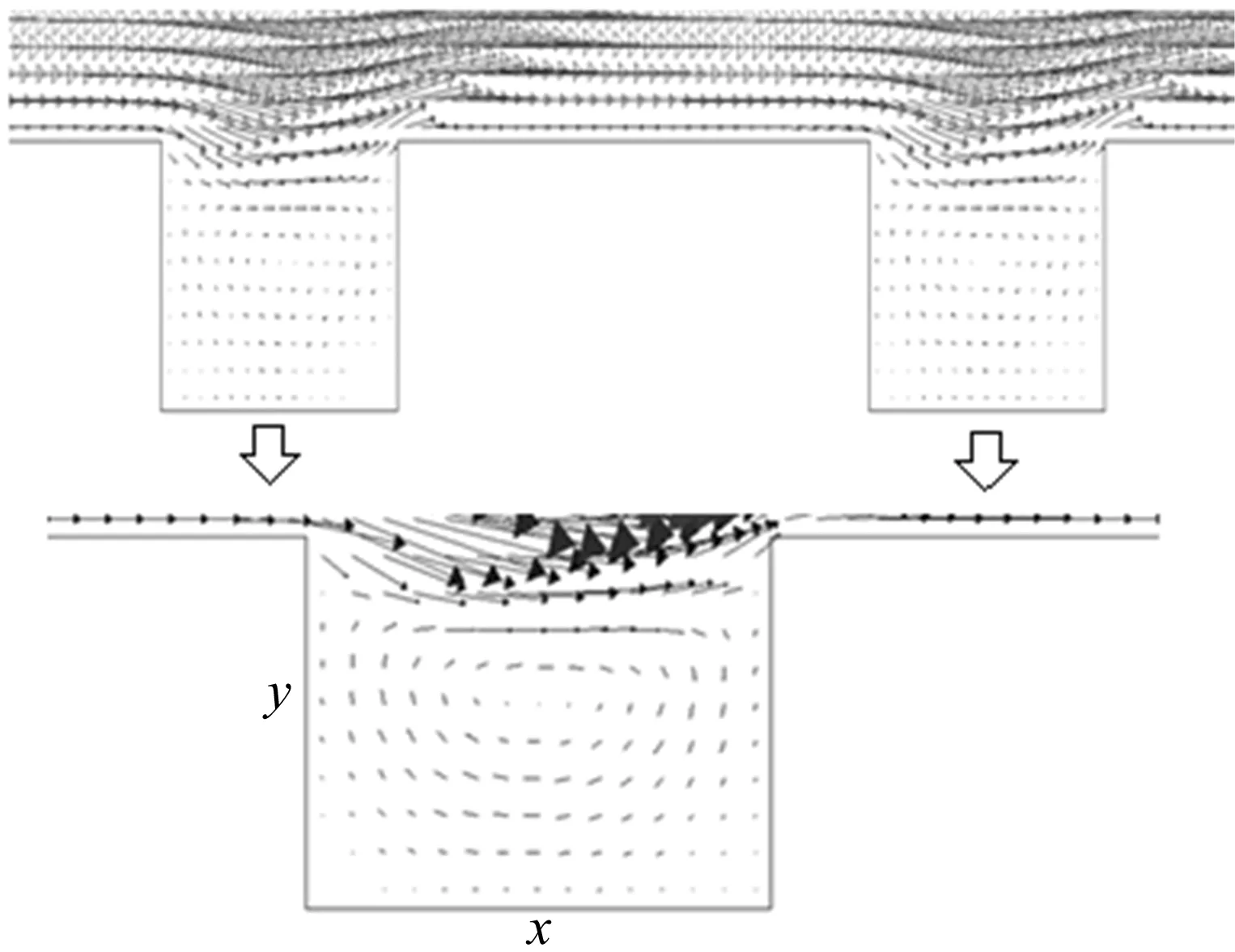
图6 局部放大的速度矢量分布(ε=1,σ=0.2)

3.3 壁面切应力分布

微凸体在两平板上均匀分布,增大了流体与壁面的接触面积。当液体黏度较大时,液体缓慢地在平板间铺展,这是壁面的粗糙度所导致的。当ε=0.5时,不同σ下壁面的切应力分布如图7所示。由图7可知，壁面切应力随微凸体波动明显,在每个微凸体处应力明显增大,而且应力增大趋势和微凸体形状保持一致,在微凸体顶端应力达到最大值。这与文献[9]的说法一致,即附加的阻力主要来自微凸体顶端。在各个微凸体处,切应力的分布基本相同,沿液体流动方向随着微凸体的波动而波动。

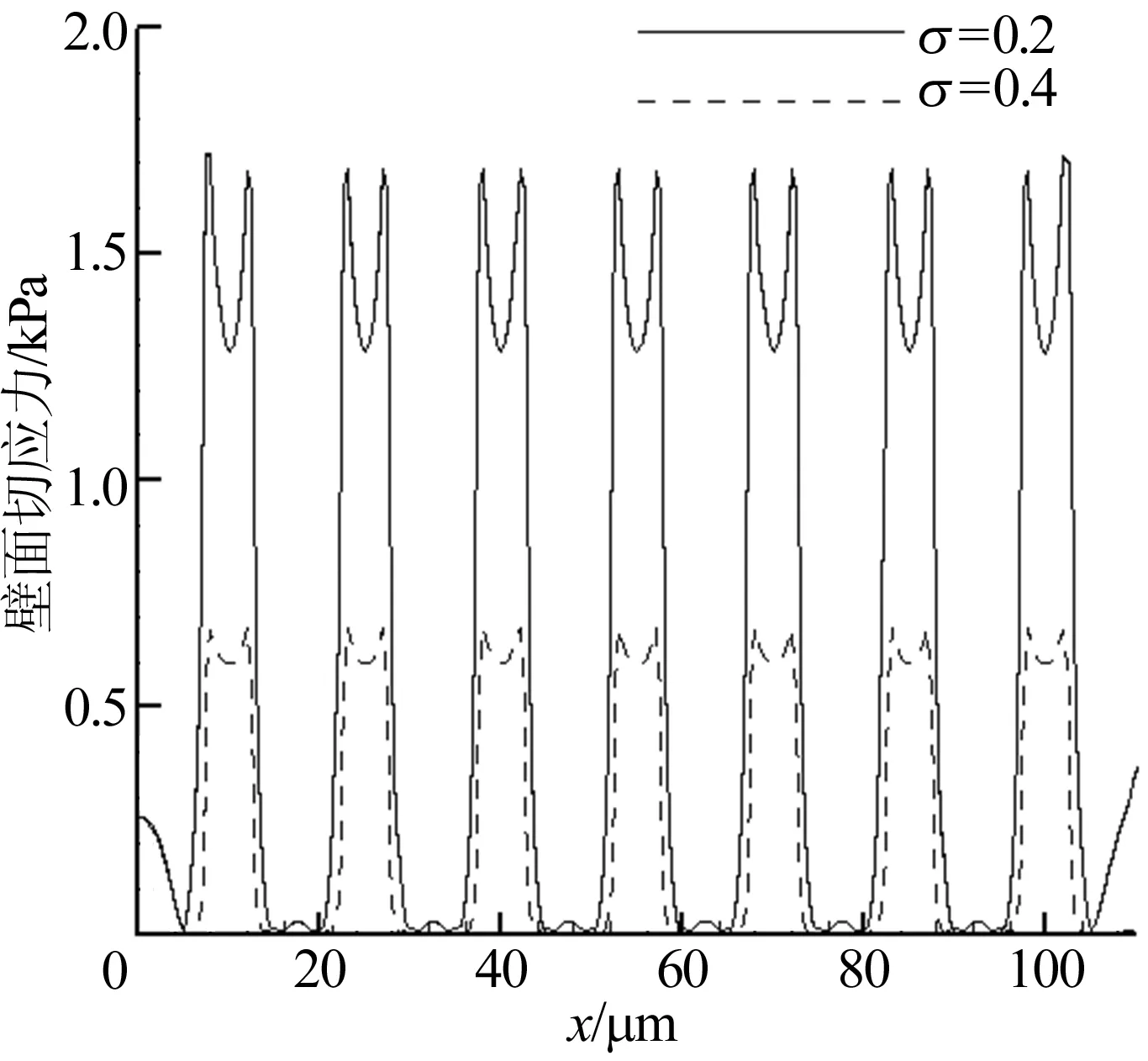
图7 壁面切应力分布(ε=0.5)

4 结 论

本文建立了粗糙接触界面间流体流动的分析模型，研究了黏性流体在压力驱动状态下的流动特性。针对不同的流动模型，重点分析了流场的速度、压强和壁面切应力的分布状态，得出了如下结论：

(1) 出口截面速度仍保持抛物线规律,并随着面积比、相对粗糙度的增大而减小。

(2) 平板中心轴压力沿流动方向波动式下降,这与微凸体的分布有很大关系;本文认为界面间层流阻力增加的来源是微凸体附近回流带来的较大压差阻力。

(3) 壁面切应力随微凸体形状而变化,在微凸体顶端达到最大值,证实了阻力主要来自微凸体顶端。

[1] 郝鹏飞,姚朝晖,何枫.粗糙微管道内液体流动特性的实验研究[J].物理学报,2007,56(8):4728-4732.

[2] 范细秋,赵晓栋,张鸿海.具有“荷叶效应”的硅基仿生表面的制备及其微摩擦性能[J].纳米技术与精密工程,2010,8(4):300-306.

[3] 沃恒洲,姚智华,王国丰,等.发动机喷嘴内部空化流动的数值模拟研究[J].合肥工业大学学报(自然科学版),2011,34(5):651-654,670.

[4] GLOSS D,HERWIG H.Microchannel roughness effects:a close-up view[J].Heat Transfer Engineering,2009,30(1/2):62-69.

[5] 殷欣,何雅玲,陶文铨,等.粗糙微通道内液体流动的多尺度耦合模拟[J].工程热物理学报,2011,32(7):1095-1098.

[6] 云和明,郭桄宇,刘智.平板微通道流动传热的粗糙元间距效应[J].机械设计与制造,2013(5):117-119.

[7] MALA G M,LI D Q.Flow characteristics of water in microtubes[J].International Journal of Heat and Fluid Flow,1999,20(2):142-148.

[8] KANDLIKAR S G.Fundamental issues related to flow boiling in minichannels and microchannels[J].Experimental Thermal and Fluid Science,2002,26(2/3/4):389-407.

(责任编辑 胡亚敏)

Effect of surface roughness on fluid flow between contact interface

LI Hao, LIU Xiaojun, ZHANG Tong, LIU Kun

(School of Machinery and Automobile Engineering, Hefei University of Technology, Hefei 230009, China)

An analysis model of the flow between rough contact interface was established in order to research the flow characteristic of pressure-driven viscous fluid between two parallel plates. In this model, the interface was simplified to two parallel plates, with the regular micro-convex body to simulate the surface roughness. Area ratio and relative roughness were established and the effect of these two physical quantities on the velocity, pressure and wall shear stress of the flow was analyzed. The results show that the reason why flow resistance increases is the large pressure resistance caused by the recirculation near the micro-convex body. Using the micro-convex body to simulate surface roughness can simplify the actual surface, and by changing the structure and distribution of the micro-convex body, the flow problem in engineering contact interface can be analyzed by this model.

contact interface; micro-convex body; area ratio; relative roughness; recirculation

2015-06-15；

2015-07-10

国家自然科学基金资助项目(51375132);高等学校博士学科点专项科研基金资助项目(20120111110026)

李 皓(1992-),女,河南襄县人,合肥工业大学硕士生; 刘小君(1965-),女,山西祁县人,博士,合肥工业大学教授,博士生导师; 刘 焜(1963-),男,陕西汉中人,博士,合肥工业大学教授,博士生导师.

10.3969/j.issn.1003-5060.2016.11.005

TH117

A

1003-5060(2016)11-1464-04