多维画法几何在多元合金相图中的应用

2016-12-16赵玉霞

滁州学院学报 2016年5期

关键词：投影图投影合金

赵玉霞

多维画法几何在多元合金相图中的应用

赵玉霞

本文根据多维画法几何的原理，应用“不等边浓度图形”阐述多元系成分表示法分析多维空间几何关系，绘制了多元系平面投影图，从而将系统成分表示法推广到七元系以上的系统。

多维画法几何；多元系相图；不等边浓度图形

多维画法几何作为图学理论的一个分支已经有很长的历史，特别是多维画法几何的理论研究，早在十九世纪40年代就开始了。但在近几十年来，越来越多的国内外学者、科学技术工作者更加关注其在科学技术领域的实际应用。用多维画法几何能够解决许多领域中多变量系统的图示表示问题，因此多维画法几何正越来越受到科技工作者的重视。在金属材料学领域里绘制金属的相图同样可以应用画法几何的原理来表示多元合金相，其中合金七元以下系统的图示法已经基本成熟[1]，但是对于合金七元以上的系统其图示方法还需要进一步研究。本文以多维画法几何为依据，通过“不等边浓度图形法”将合金系统成分图示法推广到合金七元系以上的系统，从而为绘制合金多元系相图提供新的图示方法，同时也进一步在多维画法几何实际应用。

1 多元系统“不等边浓度图形”

多元系统的成分用几何图形来表示称为浓度图形，现在用不等边图形来表示多元系的成分称为不等边浓度图形。例如，可以用不等边三角形来表示合金三元系的成分(图1所示)；用不等棱长的四面体来表示合金多元系的成分(图2所示)；四元系以上的系统其成分可用多维立体表示，其中多维立体上每一顶点表示合金一纯组元，各顶点间的间距可以不相等，因此可以用N维立体表示合金(n+1)元系统的成分。

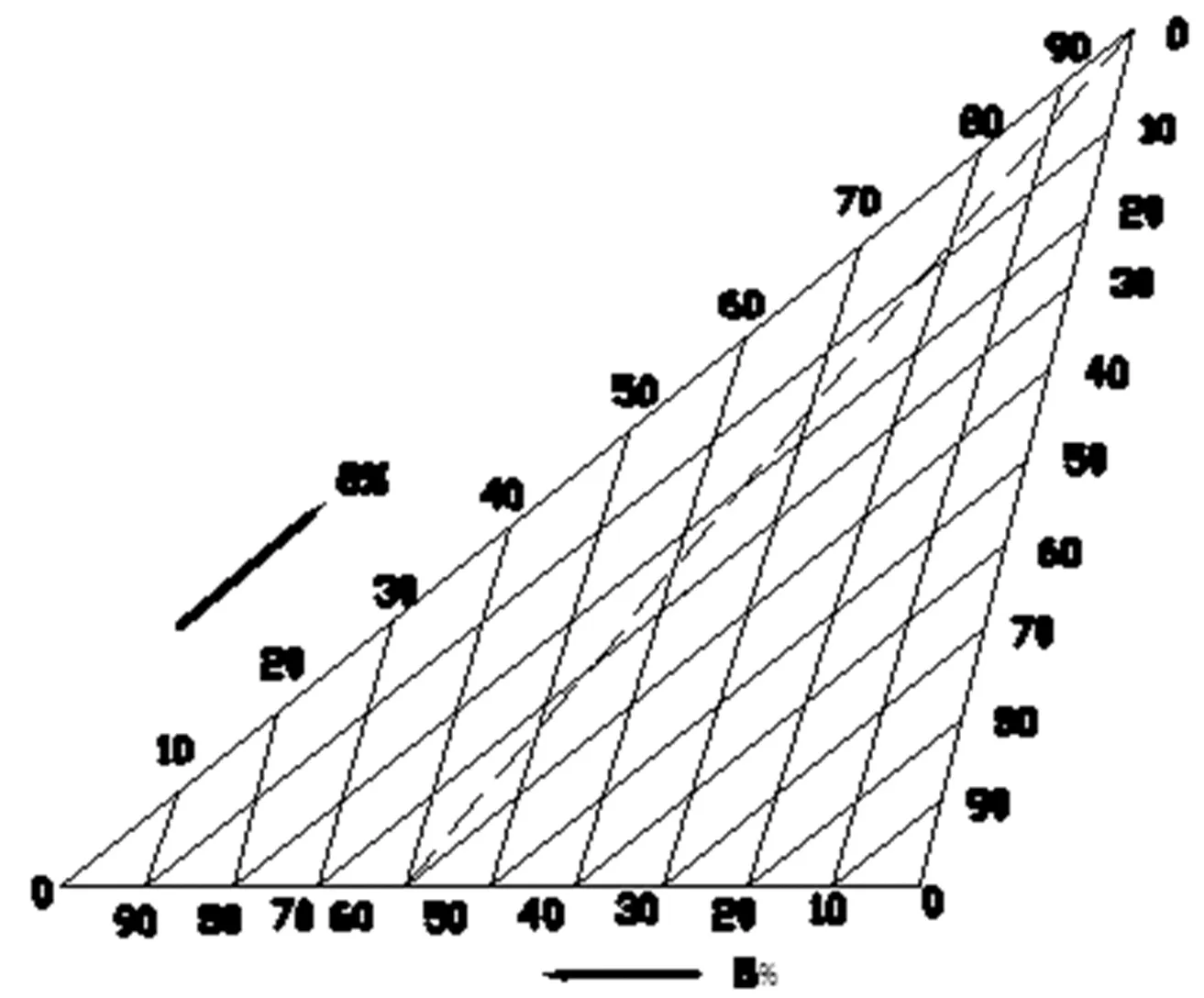
图1

图2

2 应用“不等边浓度图形”表示合金多元系成分

2.1 三元系、四元系的成分表示法

在合金三元系中将不等边浓度三角形ABC的各边100等分(图3)，每等分表示1%浓度，过 ABC中任意一点M(M点表示一个三元系)分别作各边的平行线，平行线在三角形各边所截得的线段分别表示该点各组元的浓度[2]。其中CD表示M点A组元的浓度；AE表示M点B组元的浓度；BF表示M点C组元的浓度。从图3中的几何关系还可以得出CD、AE、BF各线段表示的浓度之和必为100%。在合金四元系中可以用相似的方法，过不等棱长的四面体中任意点作各面的平行截面来表示四元系的成分。

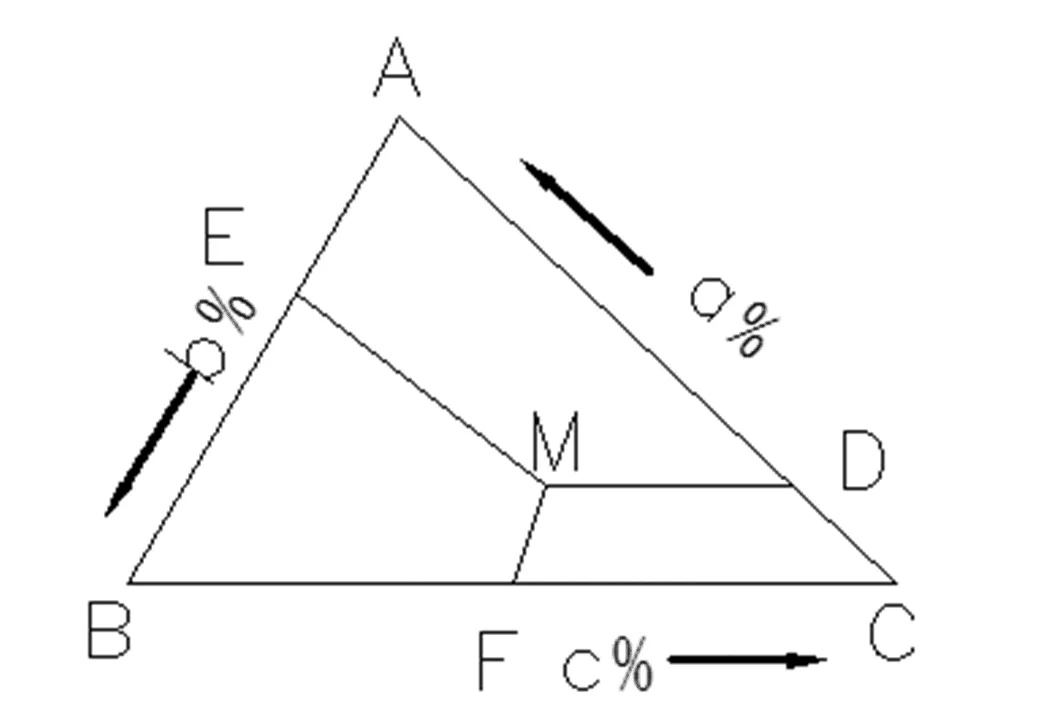
图3

2.2 十元系成分表示法

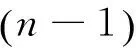
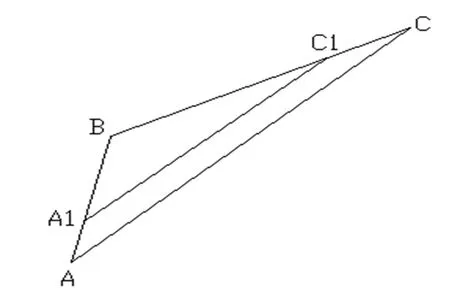
图4

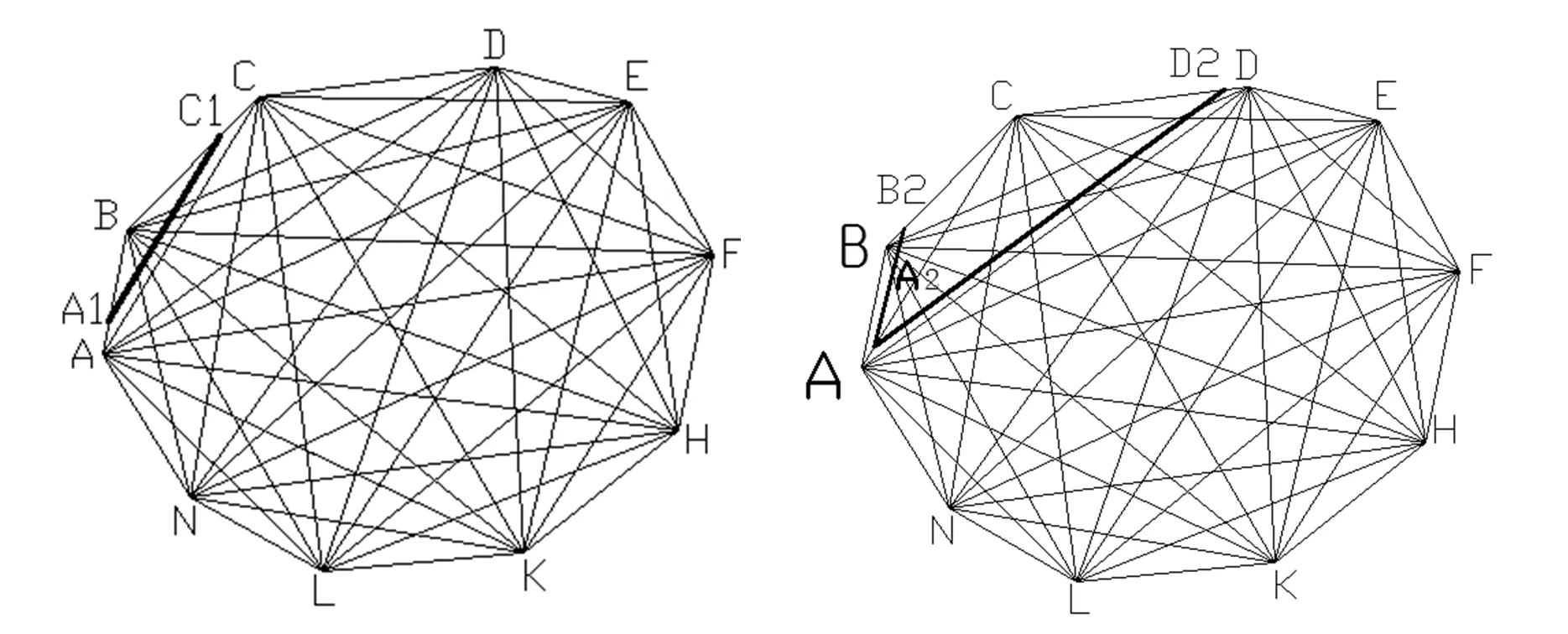
图5-1 图5-2

图5-3 图5-4

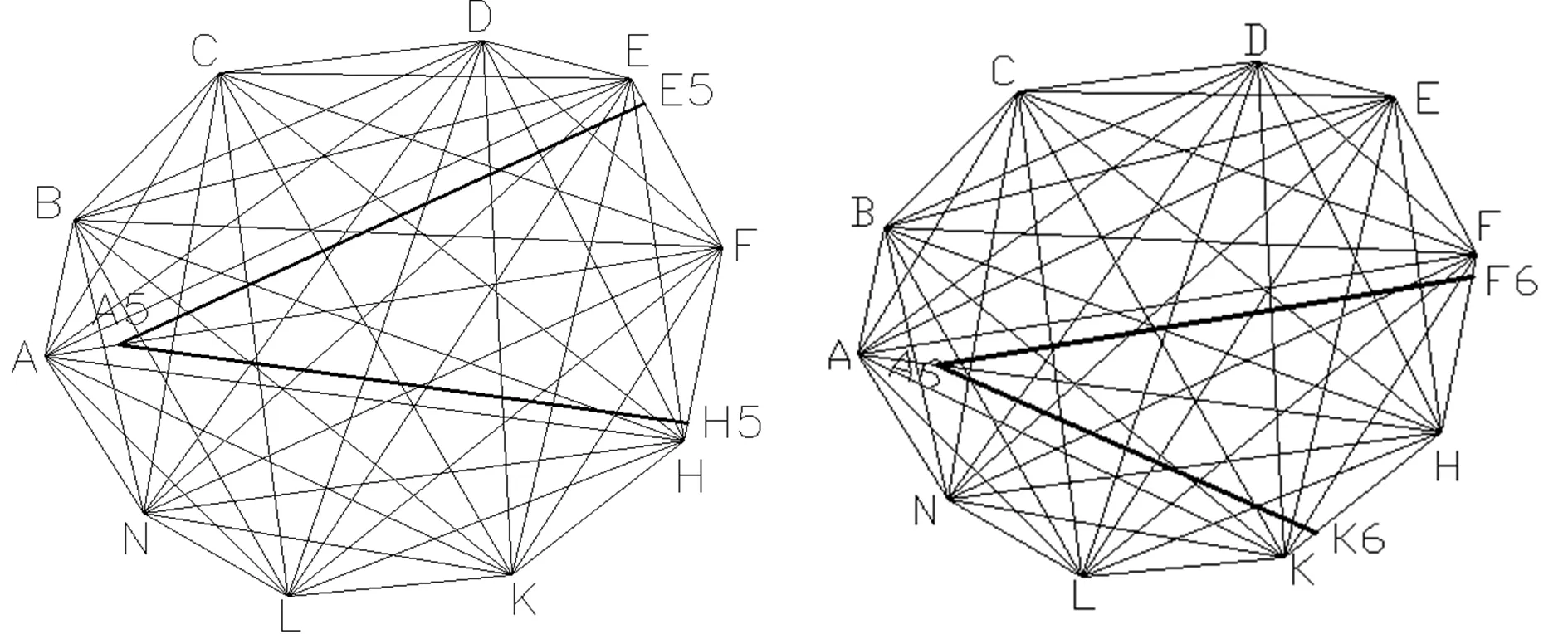
图5-5 图5-6

图5-7 图5-8

图5-9

2.3 平面投影图画法

将八个二维平面ΔABC、ΔABC、ΔACD、 ΔADE、ΔAEF、 ΔAFH、ΔAHK、ΔAKL、ΔALN按照图6进行排列，这就形成十元系的平面投影图，其中各三角形变长可取任意长度。

十元系M平面投影画图步骤如下：(图6)

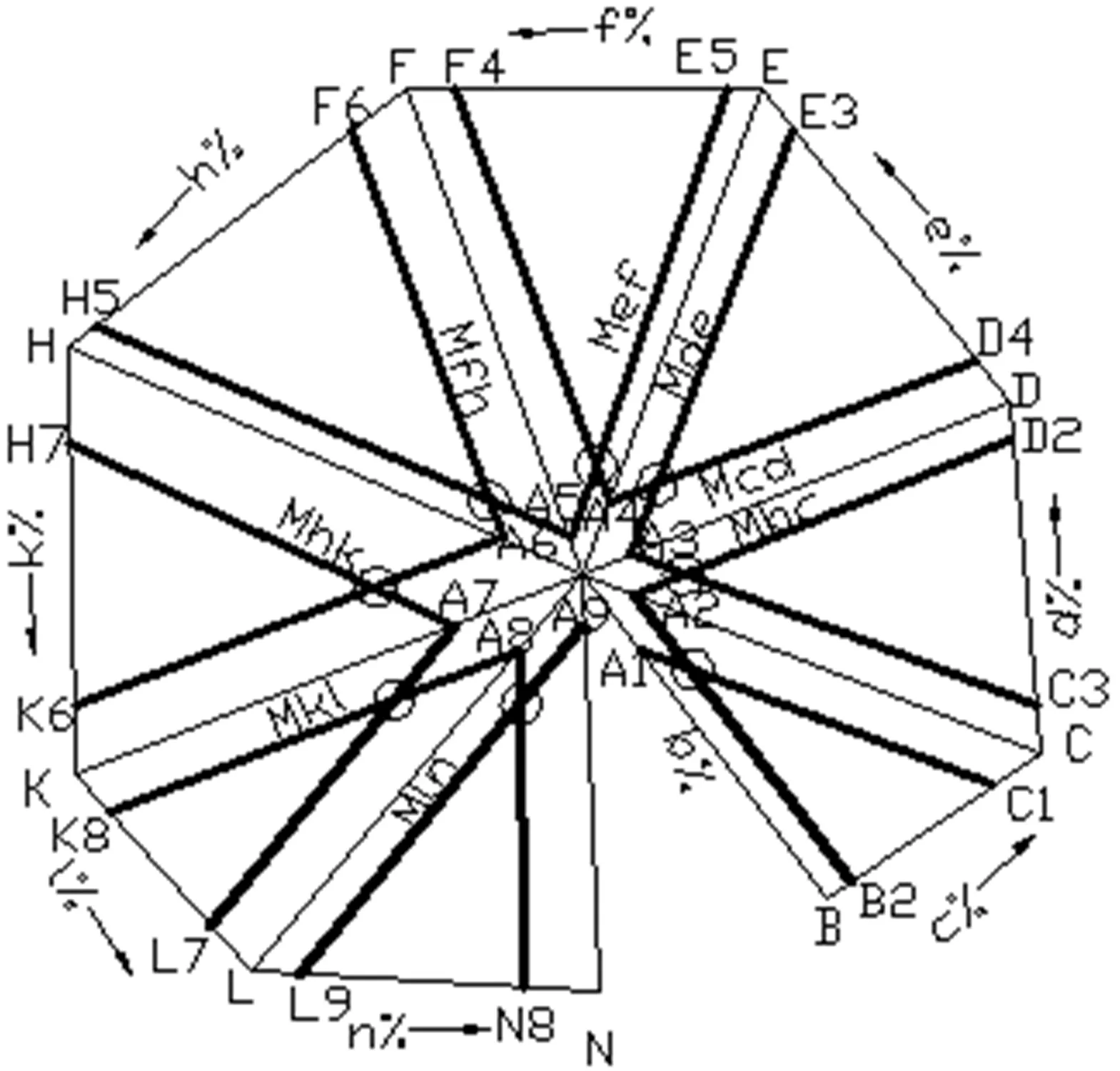
图6

在AB上截取AA1=b%，过A1作A1C1‖AC；

在AC上截取AA2=c%，过A2作A2B2‖AB，A2D2‖AD；

在AD上截取AA3=d%，过A3作A3C3‖AC，A3E3‖AE；

在AE上截取AA4=e%，过A4作A4D4‖AD，A4F4‖AF；

在AF上截取AA5=f%，过A5作A5E5‖AE，A5H5‖AH；

在AH上截取AA6=h%，过A6,作A6F6‖AF，A6K6‖AK；

在AK上截取AA7=k%，过A7作A7H7‖AH，A7L7‖AL，A7L7//AL；

在AL上截取AA8=l%，过A8作A8K8‖AK，A8N8‖AN；

在AN上截取AA9=n%，过A9作A9L9‖AL；

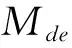
3 应用举例

已知十元合金M重20kg，分解生成两种新十元合金x和y，其中y合金重12kg，M与Y的成分如下：

合金组元%ABCDEFHKLNMab cdefhklnYaybycydyeyfyhykylynyX

其中，a+b+c+d+e+f+h+k+l+n=100，ay+by+cy+dy+ey+fy+hy+ky+ly+ny=100，求十元合金x各组元的含量。

解:(见图7)

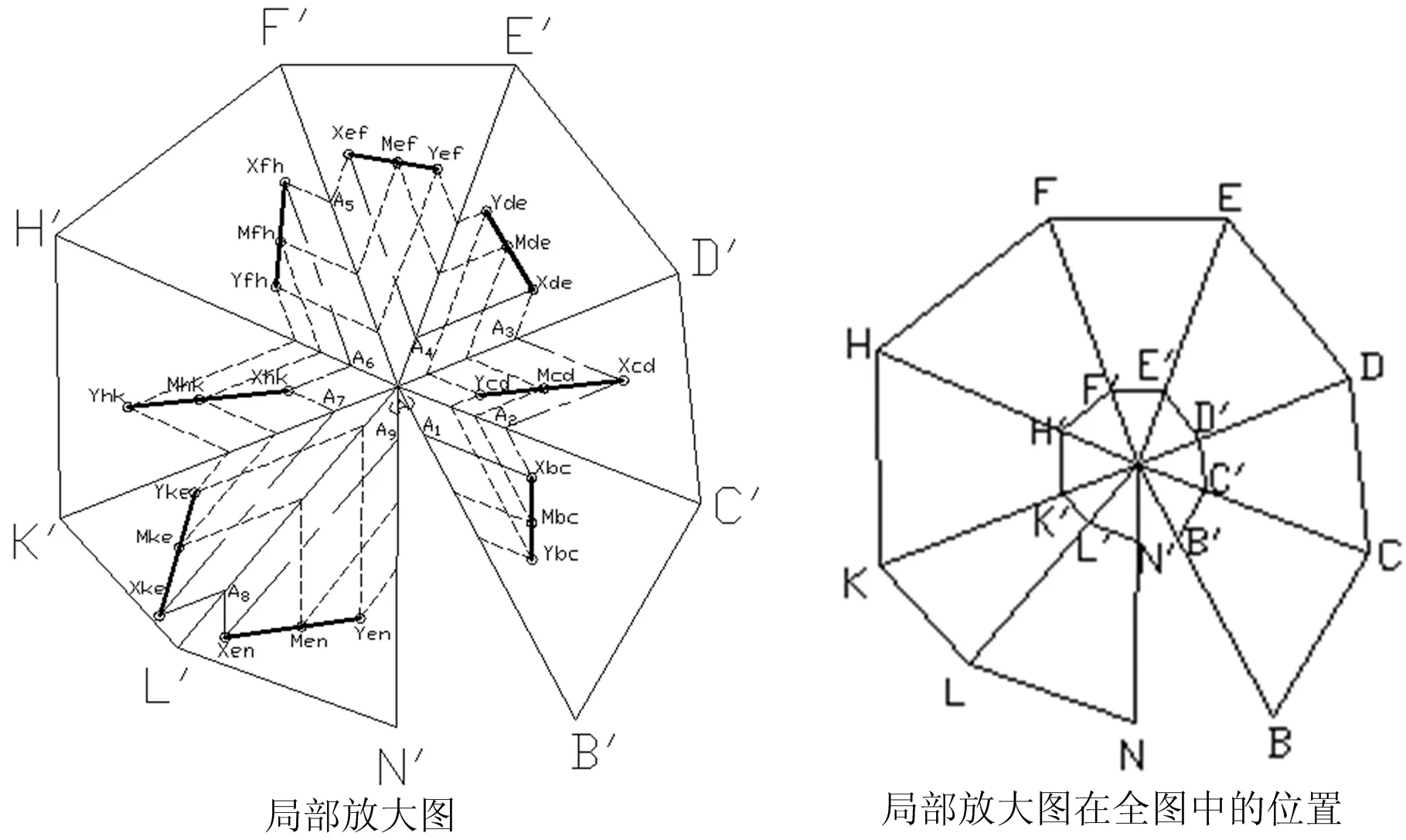
图7

第一步:根据M与Y两合金成分在平面投影图上作出M与Y的各投影点：Mbc、Mcd、Mde,、Mef、Mfh、Mhk、Mkl、Mln、Ybc、Ycd、Yde、Yef、Yfh、Yhk、Ykl、Yln.

第二步：分别连接M与Y的各对应投影点。

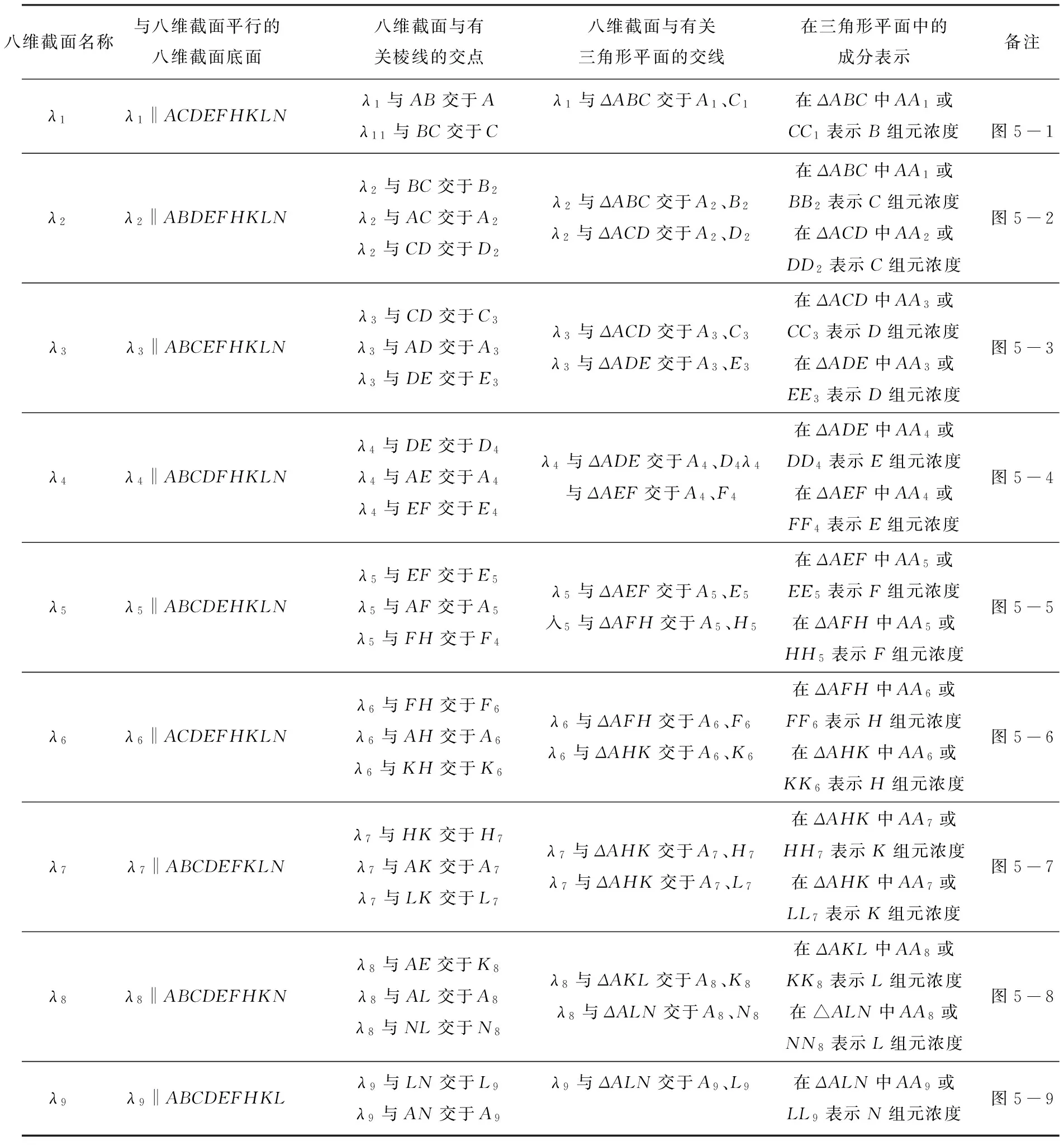
表1 过M点的八维截面一览表

第三步：根据相图杠杆定律新合金x、y的成分点必在过M点的直线上，且M点分线段xy之比与x、y的重量成反比。

式中：WM、WY、WX分别表示各十元系重量。

在平面投影图上各投影点同样服从上述杠杆定律的关系，所以新合金x与y的各投影点必在过M的相应投影点的直线上，并且M各投影点分X、Y的相应投影点连线之比与x、y的重量成反比。

在线段Yln、Mln的延长线上量取该值即得Xln点。

第四步：用同样的方法可得十元合金x的其余各投影点Xkl、Xhk、Xfh、Xef、Xde、XcdXbc.

第五步：过合金X的各投影点作相应边的平行线，即可得A1、A2、A3、A4、A5、A6、A7、A8、A9各点,分别量取AA1、AA2、AA3、AA4、AA5、AA6、AA7、AA8、AA9即得十元合金X的各组元B、C、D、E、F、H、k、L、N的百分含量(%)为：bx、cx、dx、ex、fx，hxkx，lx，nx其A组元的百分含量(%)为ax=100-(bx+cx+dx+ex+fx+hx+kx+lx+nx)。