高铁客运枢纽乘客候车时间预测模型研究

王 波，周 侃，蔡 明

（深圳市市政设计研究院有限公司，广东 深圳518029）

高铁客运枢纽乘客候车时间预测模型研究

王 波，周 侃，蔡 明

（深圳市市政设计研究院有限公司，广东 深圳518029）

为了对高铁客运枢纽乘客候车时间分析预测提供理论支撑，从探寻高铁乘客候车时间的分布特性入手，在对高铁枢纽内乘客候车时间实地调查的基础上，进行了乘客候车时间分布拟合。基于方差分析方法，对高铁枢纽内乘客候车时间影响因素进行了显著性分析，并对乘客候车时间显著性影响因素与候车时间的关系进行了探讨。利用改进的BP神经网络，构建了高铁枢纽内乘客候车时间预测模型，并利用调查数据验证了模型的有效性。分析结果表明，高铁枢纽提前购票乘客候车时间服从对数正态分布；市内出行时间、对外出行距离、对枢纽的熟悉程度、受教育水平、市内交通方式均对候车时间造成显著影响；所构建的候车时间预测模型的计算值与调查值的平均相对预测误差为11.2%，预测误差基本控制在20min以内。

交通规划；高速铁路枢纽；方差分析；神经网络；候车时间

0　引　言

我国高速铁路建设虽然起步较晚，但到目前为止已经成为世界的领跑者，无论是在速度上，还是规模上均居世界首位。随着我国高速铁路的发展，一大批高铁客运枢纽如北京南站、上海虹桥枢纽站、广州南站等如雨后春笋般陆续建成并投入使用。高铁客运枢纽一经出现便得到了社会的广泛关注，它作为多种交通方式衔接的重要节点，城市间往来的强劲纽带，无疑将集聚大量的乘客，在乘客多方式换乘中扮演着至关重要的角色。候车时间作为评价高铁枢纽服务水平和集散效率的重要指标，对其准确把握及不断优化，已经成为提高高铁枢纽服务水平的重要抓手。虽然我国在短期内积累了一些有关高铁客运枢纽设计、建设及运营管理的宝贵实践经验，但高铁客运枢纽在我国毕竟属于新生事物，有关其规划、设计、建设及管理的理论研究成果相对匮乏，有关高铁枢纽内乘客候车时间的理论研究相对不足，因此对高铁乘客的候车时间进行分析并构建其计算模型是十分必要的。

目前，乘客候车时间的相关研究已取得了一定成果，Brunetta等[1]指出乘客在机场的等候时间与出行距离有关，出行距离越长，在机场内等候的越久，且等候时间受乘客自身特性的影响，71%商务出行乘客的等候时间大于2h，而只有55%娱乐休闲出行乘客的等候时间大于2h。Tumquist[2]在研究市内公共交通车辆到达间隔对候车时间的影响时，发现随着车辆到达间隔的增大，会出现两类不同性质的乘客，一类为随机乘客，另一类为非随机乘客，前者的到达完全随机，可以认为到达时间服从均匀分布，后者的到达有一定的计划性，并通过调查验证了后者的到达服从对数正态分布。Fan等[3]指出10min的公交发车间隔为随机乘客与非随机乘客分界的发车间隔时间。Seddon等[4]对曼彻斯特地区公交乘客候车时间进行了研究，分析了乘客在公交站台的等候时间特性，建立了乘客平均等候时间与车辆到达间隔之间的回归关系模型。钟绍林等[5]对北京西站乘客的候车时间进行了调查，分析了乘客出行目的、个人属性特征、乘坐的市内交通工具等因素与候车时间的关系。何宇强、张天伟等[6,7]对我国普通铁路客运站乘客到达规律展开了分析，分析结果表明乘客的等候时间服从对数正态分布。付延冰等[8]分析了常规公交站点乘客等车过程的随机特性，根据随机过程理论推导出乘客的平均累积等车时间的计算公式，指出有效控制相邻两公共汽车离开公交站点的间隔时间并尽可能减少其波动可以缩短公交站点乘客的累积等车时间。

高铁候车时间的相关研究已引起学者们的关注和重视，但研究大多以市内常规公交和轨道交通换乘站乘客的候车时间为研究对象，且在现有的研究成果中，往往以某个因素对候车时间的影响为研究重点，缺乏多种因素影响下的高铁客运枢纽乘客候车时间量化分析方法研究。本文以高铁乘客的候车时间为研究对象，在借鉴已有相关研究成果的基础上，通过对高铁枢纽内乘客候车时间分布特性分析入手，甄别出候车时间的显著影响因素，构建提前购票乘客候车时间预测模型，并利用调查数据验证模型的有效性，为高铁枢纽设计、运营组织及服务水平优化提供参考。

1　乘客候车时间特性及其影响因素

1.1乘客候车时间分布特性分析

国外学者在研究乘客等候行为时，将乘客分为两种类型，一类乘客清楚的知道运营车辆的发车时间安排，他们往往选择一个离发车时间较近的时刻到达，以减少等候时间；另一类乘客不清楚运营车辆的发车时间，他们到达的时间较为随机。基于上述观点将乘坐高铁列车的乘客分为提前购票乘客和到站后购票乘客两类，通过问询调查发现有38.3%的乘客选择提前购票，且随着网络、手机App等查询、订票手段的不断发展完善，选择提前购票乘客的比例将会越来越高。

由于到站后购票乘客及随机乘客的到达具有很大的随机性和主观性，他们的平均等候时间可以通过式（1）[9,10]估算得到，因此本文着重对提前购票乘客候车时间进行分析。

式中：W为平均等候时间；h为平均发车间隔时间；σ为发车间隔时间的标准差。

依据国内研究现状分析可知，普通铁路枢纽的乘客候车时间近似的服从对数正态分布，其分布的概率密度函数f（t）如下：

式中：t为乘客等候时间；μ为等候时间对数的平均值；σ为等候时间对数的标准差。

参数μ和σ可以通过极大似然估计求得，估算公式如下：

通过问卷调查得到北京南站及哈尔滨西站不同候车时间对应乘客人数比例见图1。北京南站提前购票乘客的平均候车时间为61min，有80%的乘客选择在开车前80min以内到达车站。哈尔滨西客站提前购票乘客的平均候车时间为71min，有80%的乘客选择在开车前95min以内到达车站。

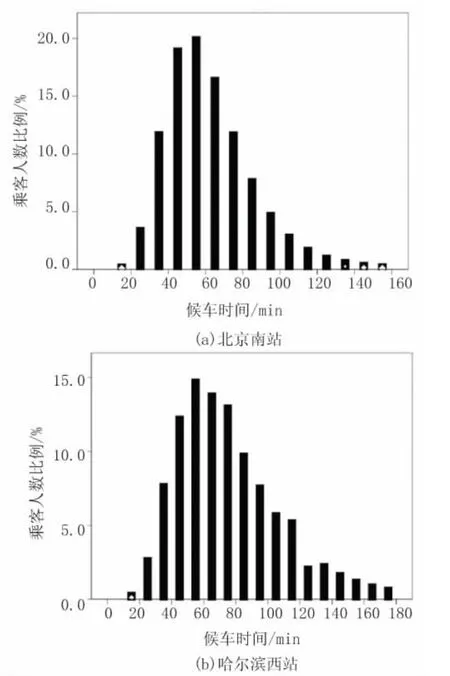
图1　乘客候车时间分布

将上述候车时间数据进行对数变换，利用柯尔莫哥洛夫-斯摩洛夫检验(K-S检验)，对变换后的数据进行正态分布检验，通过检验得出，转换后的北京南站乘客候车时间服从均值为4.112，标准差为0.357的正态分布（检验P值为0.884）转换后的哈尔滨西站乘客候车时间服从均值为4.263，标准差为0.437的正态分布（检验P值为0.731）。由此可以推断两个高铁枢纽站内提前购票乘客候车时间均服从对数正态分布。

1.2乘客候车时间影响因素筛选

高铁枢纽提前购票乘客的候车时间受出行目的、乘客年龄、对枢纽的熟悉程度等因素的综合影响[1]，论文初选乘客的性别、年龄、出行目的、市内出行时间（乘客从市内出发直至到达高铁枢纽所花费的时间）、市内交通方式（乘客到达高铁枢纽所选用的市内交通方式）、对枢纽的熟悉程度、受教育水平、对外出行距离8个因素作为高铁枢纽乘客候车时间的影响因素。通过乘客等候时间问卷调查，收集了北京南站及哈尔滨西站乘客候车时间对应的各初选影响因素的样本数据，以判断各初选因素对乘客候车时间影响的显著性。表1为利用SPSS软件对北京南站候车时间进行多因素方差分析的结果，可以看出市内出行时间、对外出行距离、对枢纽的熟悉程度、受教育水平、市内交通方式均具有统计学意义（P值小于0.05），说明它们对候车时间都具有显著性影响，而乘客年龄、乘客性别、出行目的对对候车时间的影响不显著。因此最终选取市内出行时间、对外出行距离、对枢纽的熟悉程度、受教育水平、市内交通方式作为影响乘客候车时间的5个主要因素。

表1　候车时间影响因素方差分析结果

1.3乘客候车时间影响因素分析

（1）对外出行距离对候车时间的影响 目前从北京南站出发最远抵达的城市为上海，出行里程约为1400km，从哈尔滨西站出发最远抵达的城市为大连，出行里程约为930km。由此将出行距离划分为三个等级0～500km、500～1000km及1000～1500km，不同等级出行距离对应的平均候车时间见图2。从图中可以看出随着出行距离的加长，乘客的平均候车时间也相应的加长。

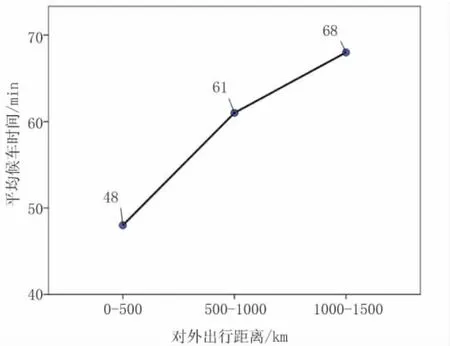
图2　出行距离与平均候车时间关系

（2）市内出行时间对候车时间的影响 通过调查得到，前往北京南站乘客的平均市内出行时间为70.8min，前往哈尔滨西客站乘客的平均市内出行时间为52.4min。图3为乘客市内出行时间与高铁枢纽内平均候车时间折线图，可以看出随着市内出行时间的增加，乘客的平均候车时间呈现出不断增加的趋势。主要原因在于，较长的市内出行时间，对应了较长的市内出行距离，出行距离的增加，加大了出行时间的不确定性，增加了乘客对市内出行时间的掌控难度，乘客往往预留的大量的富裕时间以应对这种不确定性，从而造成候车时间偏长。

图3　市内出行时间与平均候车时间关系

（3）市内交通方式对候车时间的影响 北京南站及哈尔滨西客站不同市内交通方式乘客的平均候车时间见图4，从图中可以看出步行前往枢纽的乘客的平均候车时间最短，其次为乘坐地铁到达的乘客，乘坐公交车到达的乘客平均候车时间最长，乘坐出租车和私家车到达枢纽的乘客的平均等候时间差异不明显。造成以上差异的主要原因是步行前往枢纽的乘客，其市内出行时间最容易掌控，乘客往往选择离发车时间较近的时刻前往枢纽。而地铁与出租车、私家车及公交车比较起来，最大的特点是其运行的准点率高，其市内出行时间也较容易掌控。

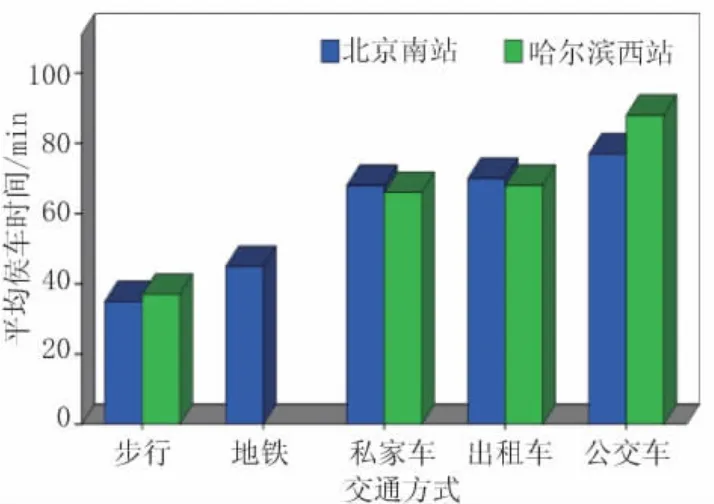
图4　市内交通方式与平均候车时间关系

（4）枢纽的熟悉程度对候车时间的影响 通过对调查数据的分析及与乘客之间的访谈发现，对枢纽的熟悉程度，也是影响候车时间的一个因素，往往对枢纽越熟悉的乘客，在其他条件相同的情况下，其候车时间往往越短。本文将对枢纽的熟悉程度分为很熟悉、较熟悉和不熟悉三个等级、不同熟悉程度的乘客的平均候车时间见图5。

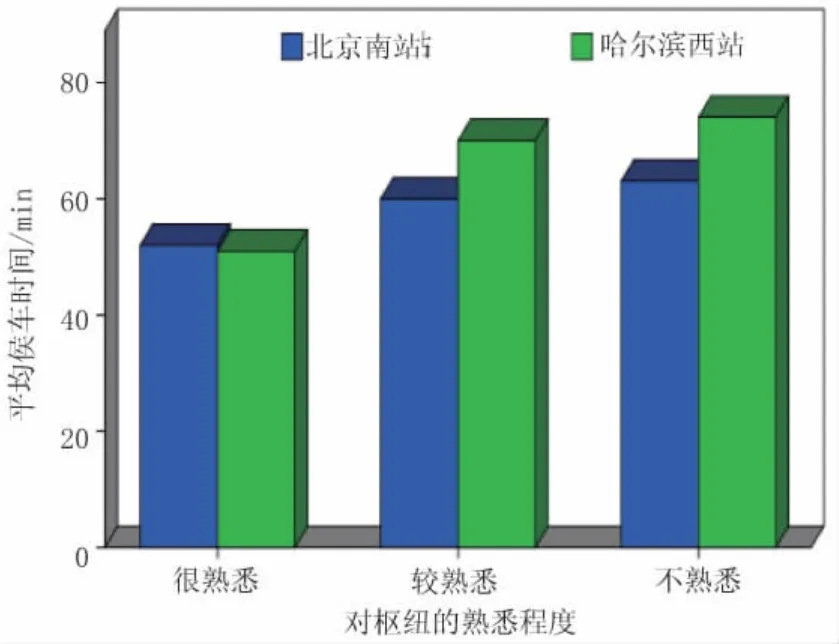
图5　对枢纽的熟悉程度与平均候车时间关系

（5）受教育水平对候车时间的影响 本文将乘客的受教育水平划分为三个等级，分别是大专及其以下、大学本科、研究生及以上。受教育水平不同的乘客对应的平均候车时间见图6。从图中可以看出随着受教育水平的提高，乘客的平均候车时间有降低的趋势，但从各组间的差异来看，受教育水平对候车时间的影响程度，明显不如论文提及的其他几个因素。

图6　不同受教育水平乘客的平均候车时间对比

2　高铁枢纽乘客候车时间预测模型

2.1预测模型选择

由于提前购票乘客候车时间受到多种因素的影响，且各种因素对其影响的叠加表现为极度的非线性，用非线性函数对提前购票乘客候车时间进行分析是十分必要的，而人工神经网络的一大特点就是非线性映射，它可以有效的解决非线性函数逼近问题，利用人工神经网络可以较为准确的拟合购票乘客候车时间与各影响因素之间的关系。因此本文选用人工神经网络作为提前购票乘客候车时间的预测模型。

2.2经典BP神经网络概述

人工神经网络具有很强的自适应、学习及抗干扰能力，人工神经网络中以BP神经网络应用最为广泛，据统计有近90%的神经网络应用是基于BP网络的[11]。

学习与训练特性是神经网络的基本特性，在BP神经网络中学习算法是误差反向传播(Backpropagation)算法[12]，该算法主要包含以下几个步骤。

第一步：对各权值wij和神经元阈值初始化，赋值为(-1，1)上分布的随机数；

第二步：随机选取第k个输入样本x（k）及对应期望输出；

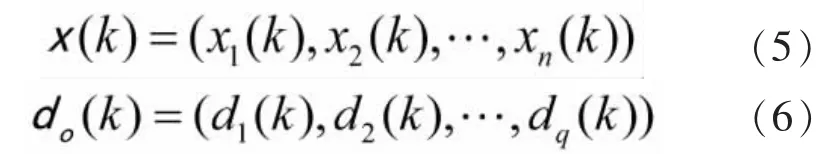
第三步：计算隐含层及输出层各神经元的输入和输出；

第四步：利用网络期望输出d0（k）和实际输出y0（k），计算误差函数E对各权值的负偏导数δ；

第五步：按照下式对各权值进行修正；

式中：wij（t+1）为调整后的权值；wij（t）为当前的权值；η为学习率；t为训练次数。

第六步：判断系统误差E其是否在允许的误差范围之内，如果在允许的误差范围之内，则结束，反之返回第二步。

2.3经典BP神经网络的不足及改进

BP神经网络的不足主要包括BP神经网络的收敛速度慢，对于一些复杂问题，BP算法需要的训练时间可能非常长；BP算法容易陷入局部极小值；通常凭借经验选择网络隐含层的层数和单元数，在一定程度上也增加了网络学习的负担，降低了网络的泛化能力。

本文主要针对BP神经网络收敛速度慢的和容易陷入局部极小值的问题进行改进，造成BP神经网络收敛速度过慢的主要原因在于，在网络不断的学习过程中，其学习率η始终保持不变，且学习率在选择上一般凭借经验，如果学习率选择过小，则模型收敛的过慢，如果学习率选择过大，则模型权值可能修正过度，导致模型震荡，反而降低了收敛效率。

因此，本文采用可变学习率的方法，来加快收敛速率，该方法的主要原理为当权值的改变真的减少了系统误差，则可以进一步增大学习率，加快收敛步伐，反之降低学习率，减少模型震荡。可变学习率η'可由式（10）表示。式中参数的典型取值为A=1.05，B=0.7，K=1.04。

为了降低BP网络产生局部极小值的可能性，在修正权值时附加一个惯性因子mc（0＜mc＜1），如公式（11）所示，使权值的调节向着误差曲面底部的平均方向变化，可以在一定程度降低BP网络产生局部极小值的可能性。

BP网络的训练误差不一定越小越好，过小的训练误差可能导致所建网络的泛化性能不足。为了提高BP网络的泛化能力，引入“提前停止”的方法，该方法将网络训练样本首先划分为训练集及验证集，其中训练集用于网络的训练，验证集用于在网络训练同时，监控网络的训练过程，在训练初始阶段，验证集形成的验证误差通常会随之网络的训练误差减小而减小，当网络开始进入过度训练时，验证误差就会逐渐增大，当验证误差达到一定程度后，网络训练将会强制提前停止，这样可以有效的控制网络的冗余性，提高网络泛化能力。

2.4基于改进的BP神经网络乘客候车时间预测

利用改进的BP神经网络对乘客候车时间进行预测，模型的输入层单元数由论文筛选的候车时间影响因素个数决定，由此输入层单元数为五个，输出层为提前购票乘客候车时间。

关于模型隐层的数量，与所要分析问题的复杂程度密切相关，目前还没有一个的公认确定方法，大多数是凭借经验确定，经验表明，对于简单的分析问题，一个隐层足够满足分析要求，当问题较为复杂时，采用双层隐层结构，有利于提高神经网络的性能。考虑到候车时间的随机性较强，且其影响因素众多，因此论文选用双层隐层结构。

关于单个隐层单元数，通常采用经验估算公式进行确定，经验估算公式见表2。根据本模型的输入单元数及输出单元数，依据经验公式，计算得到单个隐层单元数在3～13个之间较为合适，本文选取中间值8个，作为第一层隐层的单元数，当采用多层隐层结构时，第一个隐层单元数与第二个隐层单元数的比约为3∶1时[13]，可以提高网络性能，因此确定第二个隐层的单元数为3。

表2　 隐层单元数目的经验估算公式[14]

理论上讲任意连续的非多项式函数都可以作为BP网络的传递函数，但Sigmoid型函数有其自身的优点，如光滑性及方便求导，而在权值的反向传播计算过程中，要计算传递函数的导数，选用Sigmoid型函数作为传递函数可以节省计算的存储空间并提高模型的收敛速度，常用的Sigmoid型函数有logsig及tansig，因此确定第一个隐层的传递函数为logsig，第二个隐层的传递函数为tansig。为了扩大模型的输出范围，提高模型的泛化能力，确定输出层的传递函数为purelin。最终确定的候车时间神经网络预测模型结构见图7，学习算法采用改进后的BP算法。模型输入变量中分类变量的编码见表3。

图7　候车时间BP神经网络预测模型

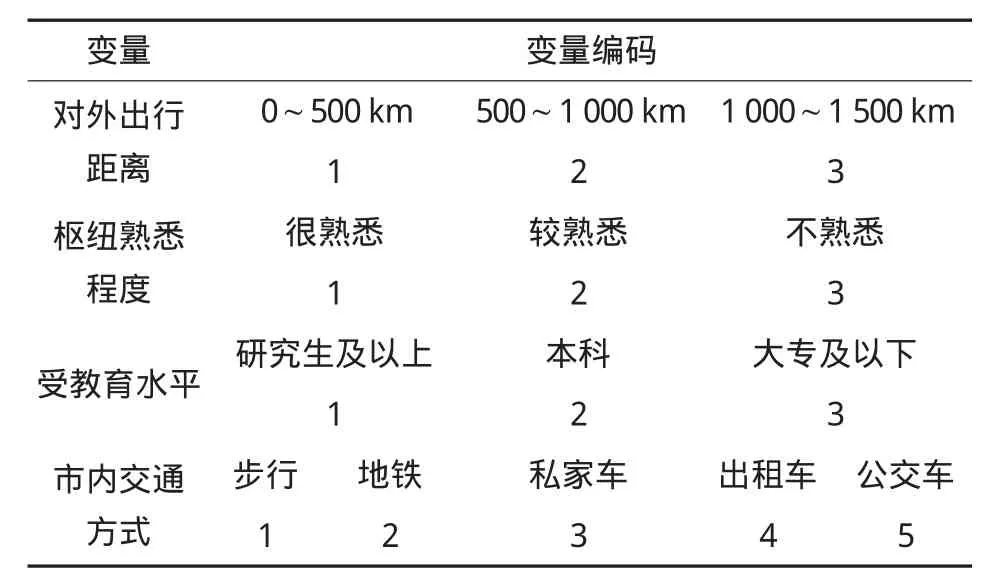
变量　变量编码对外出行距离0～500km　500～1000km　1000～1500km 1 2 3枢纽熟悉程度很熟悉　较熟悉　不熟悉1 2 3受教育水平　研究生及以上　本科　大专及以下1 2 3市内交通方式步行　地铁　私家车　出租车　公交车12　3　45

利用调查所得的北京南站720个乘客等候时间样本数据，对预测模型进行标定，随机抽取四分之三的样本用于训练，剩余四分之一的样本构成训练过程中的验证集，由于输入参数中市内出行时间与其余几个分类变量的编码在数量级上差别较大，在模型训练前首先利用matlab中的数据归一化函数premnmx[15]，对输入参数进行归一化处理。模型设定的训练步数为8000，训练期望误差为0.005，模型参数A=1.05，B=0.7，K=1.04，mc=0.9。训练过程中的训练误差与验证误差曲线见图8，从图8中可以看出在训练初始阶段，验证集形成的验证误差通常会随之网络的训练误差减小而减小，当训练步数达到4500步左右时，验证误差开始增大，训练步数达到6217步时训练强制停止，此时的训练误差为0.214。

图8　训练误差与验证误差曲线

3　候车时间预测模型验证

利用训练过后的候车时间预测模型对哈尔滨西客站336个乘客候车时间调查样本进行预测，等候时间调查结果与预测结果的对比见图9，等候时间预测误差见图10，从图9、图10中可以看出，预测结果与调查结果较为吻合，大多数预测误差在正负20min以内，平均相对预测误差为11.2%。以上结果表明，预测结果具有一定的准确性，所构建的预测模型是可行的。

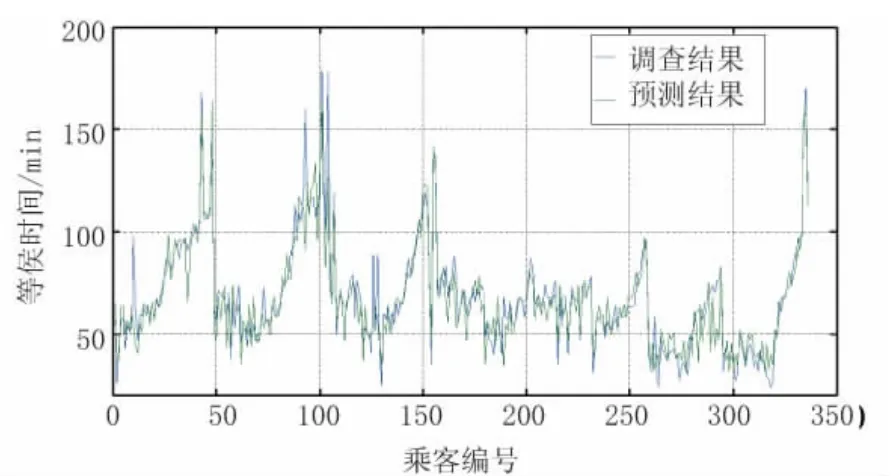
图9　等候时间预测与调查结果对比

图10　等候时间预测误差

4　结　语

（1）通过对高铁客运枢纽提前购票乘客候车时间时间分布特性的统计分析，发现乘客候车时间服从对数正态分布。

（2）利用方差分析手段分析了乘客的性别、年龄、出行目的、市内出行时间、市内交通方式、对枢纽的熟悉程度、受教育水平、对外出行距离8个因素对高铁客运枢纽提前购票乘客候车时间的影响，依据分析结果发现市内出行时间、对外出行距离、对枢纽的熟悉程度、受教育水平、市内交通方式均对候车时间影响显著。

（3）分析了传统BP神经网络模型的不足，并给出了改进方法，利用改进的BP神经网络构建了高铁客运枢纽提前购票乘客候车时间预测模型并标定了模型的参数，利用实地调查数据验证了模型的有效性。

[1]LorenzoBrunetta,LucaRighi,GiovanniAndreatta.Anoperations researchmodelfortheevaluationofanairportterminal:SLAM (simplelandsideaggregatemodel)[J].JournalofAirTransport Management,1999,5(3):161-175.

[2]Tumquist,M.A..Strategiesforimprovingreliabilityofbustransit service[J].TransportationResearchRecord,1981,818:7-13.

[3]WeiFan,RandyB.Machemehl.Characterizingbustransitwaiting times[C].ProceedingsoftheSecondMaterialSpecialtyConference oftheCanadian,2002.

[4]SeddonPA,DayMP.Buspassengerwaitingtimeingreat manchester[J].TrafficEngineeringandControl,1974,15(9):422-445.

[5]钟绍林,王修华,何宇强,等.北京西站客流集散特征调查[J].铁道运输与经济,2005,27(2):37-39.

[6]何宇强,毛保华,陈绍宽,等.铁路客运站旅客最高聚集人数计算方法研究[J].铁路学报,2006,28(1):6-11.

[7]张天伟.铁路客运站旅客聚集规律研究[J].铁路学报,2006,31(1): 31-34.

[8]付延冰,陈治亚.基于随机分析的公交站点乘客等车时间[J].系统工程,2009,27(6):119-122.

[9]WeldingP.I.Theinstabilityofaclose-intervalservice[J].Operational ResearchQuarterly,1957,8(3):133-142.

[10]OsunaE.E,NewellG.F.Centralstrategiesforanidealizedpublic transportsystem[J].TransportationScience,1972,6(1):52-72.

[11]SimonHaykin.神经网络原理[M].北京:机械工业出版社,2004.

[12]董长虹.Matlab神经网络与应用 [M].北京:国防工业出版社, 2005.

[13]王吉权.BP神经网络的理论及其在农业机械化中的应用研究[D].辽宁沈阳:沈阳农业大学,2011.

[14]飞思科技研发中心.神经网络理论与MATLAB7实现[M].北京:电子工业出版社,2005.

[15]张磊,郭莲英.MATLAB实用教程[M].北京:人民邮电出版社, 2008.

U491.6

A

1009-7716（2016）11-0114-06

10.16799/j.cnki.csdqyfh.2016.11.033

2016-07-01

王波（1974-），男，辽宁本溪人，高级工程师，从事城市交通规划研究工作。