有轨电车嵌入式轨道板温度翘曲变形量研究

易 欣 杨 刚 刘光胜

(1.广深铁路股份有限公司广州工务段,510600， 广州; 2.成都市新筑路桥机械股份有限公司,611430,成都∥助理工程师)



有轨电车嵌入式轨道板温度翘曲变形量研究

易 欣1杨 刚2刘光胜2

(1.广深铁路股份有限公司广州工务段,510600， 广州; 2.成都市新筑路桥机械股份有限公司,611430,成都∥助理工程师)

选取已铺轨并覆盖200 mm绿化土的嵌入式轨道板,对其温度梯度及高程变化进行连续24 h 观测,以研究气温变化对轨道板温度梯度及翘曲变形的影响。采用理论方法和有限元数值方法计算轨道板翘曲变形,并将计算结果与实测值进行对比分析,为嵌入式轨道的结构设计提供参考。结果表明:在24 h观测时间内,轨道板温度梯度基本为正,其最大值为10.4 ℃/m。在最大正温度梯度作用下,轨道板最大翘曲变形为0.028 0 mm。通过理论计算和数值计算得到的最大翘曲位移分别为0.019 4 mm和0.027 0 mm。二者均与现场测量结果接近,验证了温度实测数据、有限元数值计算模型及边界条件的准确性和可靠性。

有轨电车; 嵌入式轨道; 温度梯度; 翘曲变形

First-author′s address Guangzhou Track Maintenance Division,Guangzhou-Shenzhen Railway Co.,Ltd.,510600,Guangzhou,China

有轨电车嵌入式轨道结构使用高弹性的聚氨酯材料替代传统轨道的扣件系统,其钢轨完全由承轨槽内的聚氨酯材料及轨下弹性垫板固定和支撑[1]。轨道结构由59R2槽型钢轨、高分子填充材料、嵌入式轨道板、自密实混凝土、底座、路基等部分组成,其结构横断面如图1所示。

图1 轨道结构横断面图

当气温变化时,混凝土材料的导热性能差,于是轨道板面和板底之间存在温度差。温度差通常由温度梯度(轨道板温度梯度=(板面温度-板底温度)/板厚度)来表示。轨道板厚度越大,板面与板底的温度差也越大。在温度梯度荷载作用下,轨道板会发生温度翘曲变形[2-3],从而引起两个问题:①轨道板与自密实混凝土层间粘结关系破坏,层间出现离缝;②层间离缝会降低自密实混凝土层对轨道板的约束作用,从而引起轨道板横纵向几何形位发生变化。

目前，国内在高速铁路方面已有针对板式轨道翘曲变形的研究。文献[4-5]对CRTSI型轨道平板和框架板进行了温度测试,提出无论平板还是框架板,其上下表面温差最大值均发生在13—15点,温度梯度约为52.6～68.4 ℃/m。文献[6-7]对CRTSII型轨道板进行了长达半年的观测,提出轨道板板面温度、温度梯度均与气温变化规律一致,且随着轨道结构深度的增大,温度和温度梯度的波动幅度均逐渐减小；板面温度的高低决定了轨道板温度梯度的大小。

由于轨道结构形式存在差异,嵌入式轨道板温度翘曲研究不能照搬其研究成果。其差异主要有三个方面:①板厚不同。嵌入式轨道板厚260 mm，比高铁上200 mm的轨道板厚；而轨道板厚度决定了上下表面温度梯度的大小。②覆盖方式不同。嵌入式轨道板表面有200 mm的覆土,而高铁上的轨道板无覆盖；这对轨道板温度梯度的影响很大。③限位方式不同。嵌入式轨道板通过其下的自密实混凝土层和门型钢筋进行限位,而高铁上的轨道板限位则由凸型挡台或板间纵连来实现。

嵌入式轨道板是有轨电车的主要承载部件。目前，国内尚无嵌入式轨道结构设计理论。温度梯度荷载常年作用于轨道板,需通过实测温度数据导入力学模型分析对其轨道结构的影响，并据此判断其在嵌入式轨道轨道结构设计中是否作为主要作用荷载。因此,本文基于成都市有轨电车嵌入式轨道试验段的轨道板温度梯度实测结果,采用有限元法和理论解法对嵌入式轨道结构在温度梯度作用下的翘曲变形进行研究,为该轨道结构的推广应用提供理论依据。

1 轨道板温度梯度及翘曲变形观测试验

1.1 试验概况

2014年5月26日16: 00～2014年5月27日16:00,对成都市有轨电车嵌入式轨道试验段进行气温、轨道板温度梯度及温度翘曲变形的观测。试验期间天气晴朗,最高气温30.4 ℃。观测频次为1次/h。

采用温度计测量大气温度,并用测温枪测量承轨槽顶部温度。在轨道板板面和板底布置温度传感器,共布置9个测点(板面6个,板底3个)。测点布置详见图2。采用百分表对轨道板翘曲变形进行测量,并用全站仪进行校核。变形观测点具体位置如图3的点1#～6#所示。

图2 成都有轨电车轨道板测温点布置

1.2 温度梯度观测结果分析

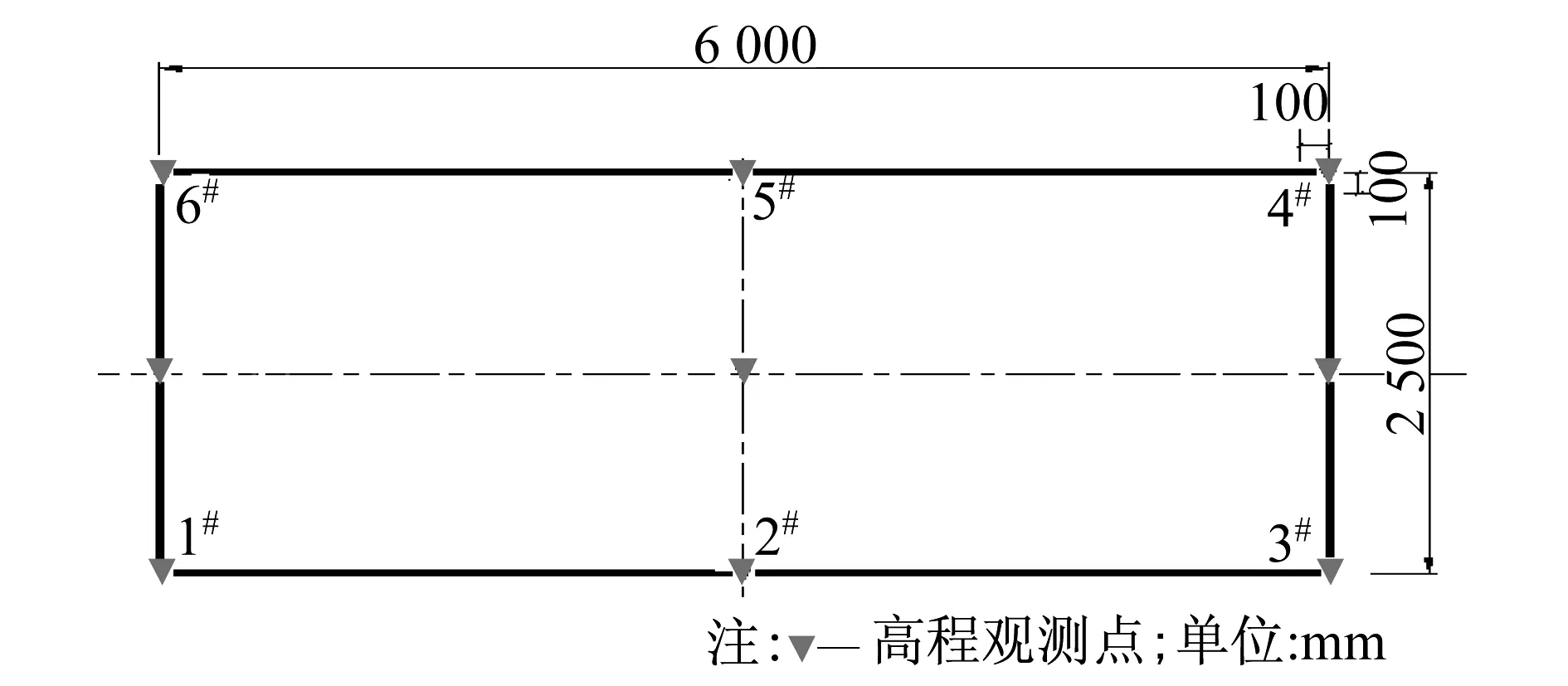
图3 轨道板翘曲变形观测点平面布置

温度和温度梯度的观测结果如图4所示。由图可知:①在24 h测试时间内,轨道板板面和板底最大温差值为2.7 ℃；仅出现正温度梯度,且其值较小,最大值仅为10.4 ℃/m。②当气温最高时,正温度梯度达到最大值；当气温最低时,正温度梯度降至最低值；变化范围为0～10.4 ℃/m。③承轨槽顶面温度变化基本与气温一致,而轨道板温度变化与气温相差较大,且其变化幅度较小。

图4 试验轨道板温度变化及温度梯度曲线

经分析，可得以下结论:

(1) 嵌入式轨道结构表面覆盖有200 mm厚的绿化填土,所测承轨槽顶面温度与其底面温度相差较大,而轨道板板面温度与承轨槽底部温度几乎相同。可见，覆盖填土对于轨道板上下表面温差起决定性作用。故计算温度梯度时,轨道板上表面温度为覆盖填土下的板面温度,而非承轨槽顶面温度。

(2) 嵌入式轨道板出现最大温度梯度(15:00—17:00)及最小温度梯度(6:00—8:00)的时间较普通裸露在大气中的板有将近2 h的延迟。普通板最大正、负温度梯度分别出现在(13:00—15:00)和4:00左右[7]。

(3) 在24 h测试时间内,轨道板基本为正温度梯度。这与高铁上板式轨道测试结果有很大的不同[5-6]。由于轨道板位于土层以下,其四周均填土夯实,并与空气相互隔绝,故自密实混凝土的水化作用和路基的散热均较缓慢。这导致轨道板温度变化速率随轨道结构深度的增加逐渐降低,从而板面和板底温度变化都很小。

1.3 翘曲变形观测结果分析

轨道板温度翘曲变形规律如图5所示。

图5 轨道板温度翘曲变化规律

由图可知,当温度梯度最大时(15:00—17:00),翘曲变形值最大,为0.028 0 mm;当温度梯度较小时(6:00—8:00),翘曲变形值接近0。轨道板产生的翘曲变形量在0～0.028 0 mm之间变化。

分析可得，在15:00—17:00时段轨道板处于正温度梯度作用,而此时，气温最大值也同时出现。由于混凝土自身的膨胀大于板角下翘值,因此试验测得的翘曲变形为正值。由此可见,轨道板的翘曲位移量很小。

2 轨道板温度翘曲变形分析

2.1 力学模型及参数

本文采用有限元法分析温度梯度作用下嵌入式轨道板翘曲位移的影响。其中，轨道板、自密实混凝土、底座板均采用实体单元模拟,其弹性模量分别为3.45×104MPa、3.25×104MPa和3.25×104MPa,泊松比均为0.20;钢轨、门型钢筋采用梁单元模拟,其弹性模量分别为2.06×105MPa和2.00×104MPa,泊松比均为0.30;高分子填充材料采用三向弹簧单元模拟,其垂向刚度为103 MPa,纵向刚度为34.2 MPa,横向刚度为41.3 MPa。轨道板长6 000 mm,宽2 500 mm,厚260 mm。轨道板下自密实混凝土层厚度为120 mm。基于现场测试结果,最大温度梯度取值为10.4 ℃/m。

模型考虑了轨道结构自重及门型钢筋对轨道板翘曲变形的影响,并假设下部基础无变形(即不考虑下部基础的变形)。根据嵌入式轨道结构本身的特点,层间关系采用全粘结。计算模型如图6所示。

图6 嵌入式轨道板理论计算模型

2.2 有限元计算结果分析

轨道板翘曲变形云图如图7所示。由图可知，嵌入式轨道板在正温度梯度作用下的翘曲变形较小,最大变形量为0.019 4 mm。

图7 轨道板翘曲变形云图(放大1 000倍)

经分析，在正温度梯度作用下,轨道板板端向下翘,板中上拱；而承轨槽顶却出现了向上的最大翘曲量。这是因为承轨槽顶直接裸露在大气中,造成承轨槽上下表面温差很大,从而引起混凝土自身的热胀位移大于其下翘值。

3 数值解、理论解和实测结果的对比分析

[11],对轨道板在温度梯度作用下的翘曲变形进行理论计算。计算温度梯度取现场实测的最大温度梯度10.4 ℃/m。

轨道板作为一种温度线弹性体,其翘曲变形量与发生变形前后的温度梯度成正比,为:

ΔL=αTnL

(1)

式中：

α——温度变形系数,根据美国阿灵顿道路试验结果可知α=0.000 01;

Tn——轨道板翘曲前后的温度梯度;

L——轨道板厚度。

将有限元计算的数值解、理论解以及现场试验得到的轨道板最大翘曲位移进行对比,如表1所示。

表1 不同方法得到的轨道板最大翘曲变形量 mm

通过表1可得以下结论:

(1) 理论解与现场试验结果基本吻合,且数值解与理论解和实测数据相差不大,二者偏差不超过5%,验证了计算结果的准确性和可靠性。

(2) 三种方法得到的翘曲位移均不足0.05 mm,远小于高速铁路普通板式轨道翘曲变形量[12]。这说明嵌入式轨道结构比普通的板式轨道结构稳定,其受到温度荷载的影响很小。

4 结论

(1) 嵌入式轨道结构表面的覆盖填土对于轨道板上下表面温差起决定性作用;在实测中气温最高的时候,轨道板板面温度和板底温度差值最大为2.7 ℃;轨道板位于土层以下,其四周均填土夯实,并与空气相互隔绝,在24 h观测时间内,轨道板基本为正温度梯度,且其值较小,最大正温度梯度仅为10.4 ℃/m。

(2) 当温度梯度最大时(15:00—17:00)时,翘曲变形值最大,为0.028 0 mm;当温度梯度较小时(6:00—8:00),翘曲变形值接近0。由于覆盖填土的作用,嵌入式轨道出现最大、最小温度梯度的时间较裸露在大气中的轨道板有2 h的延迟。这与填土的保温、吸热功能相关。

(3) 数值计算及理论计算得出的最大翘曲位移分别为0.019 4 mm和0.027 0 mm。二者均与现场测量结果接近。本文测量结果可作为成都地区嵌入式轨道温度实测数据,其有限元数值计算模型及边界条件准确可靠。

参考文献

[1] 牛月明,戴月辉.钢轨嵌入式轨道结构及其设计优化[J].城市轨道交通研究,2003(6):100.

[2] 赵国堂.高速铁路无碴轨道设计[M].北京:中国铁道出版社,2005.

[3] 刘学毅,赵坪锐,杨荣山,等.客运专线无砟轨道设计理论与方法[M].成都:西南交通大学出版社,2010.

[4] 王森荣,孙立,李秋义,等.无砟轨道轨道板温度测量与温度应力分析[J].铁道工程学报,2009(2)52.

[5] 王森荣.板式无砟轨道温度力研究[D].成都:西南交通大学,2007.

[6] 刘钰,陈攀,赵国堂.CRTSⅡ型板式无砟轨道结构早期温度场特征研究[J].中国铁道科学,2014(1):1.

[7] 刘钰.CRTSII型板式轨道早期温度场特征及其影响研究[D].成都:西南交通大学,2013.

[8] 王继军,尤瑞林,王梦,等.单元板式无砟轨道结构轨道板温度翘曲变形研究[J].中国铁道科学,2010(3):9.

[9] 邵丕彦,李海燕,吴韶亮,等.CRTSI型轨道板温度变形及与砂浆垫层间离缝的测试研究[J].中国铁道科学,2013(2):18.

[10] 周毅,何燕平,杨荣山.CA砂浆弹摸对框架板式轨道翘曲应力的影响分析[J].铁道建筑,2011(3):103.

[11] 邓学钧,陈荣生.刚性路面设计[M].北京:人民交通出版社,2004.

[12] 朱晓嘉.CRTSⅡ型轨道板温度效应及其对列车运行安全性的影响分析[D].成都：西南交通大学,2012.

福州首条地铁5月18日投入试运营

为期3天的福州地铁试乘活动5月13日上午开始，吸引了榕城市民积极参与。人民网记者与市民一道参与了当天试乘活动，并通过人民网福建频道微博和微信平台直播了试乘体验盛况。记者在现场看到，参加试乘的市民群众井然有序地进入地铁口，通过安检、刷票进站上车，并主动为老人让座。现场工作人员和民警热情地接受乘客咨询，解答各种具体问题，不失时机地宣传安全乘车、文明出行观念。当天开放试乘的是福州地铁1号线南段，全长9.76 km，设三叉街站、火车南站站等9个站点。福州地铁采用的列车由位于福建泉州的中车公司组装生产，标准载客数为1 460人，超员载客数为2 062人，跑完南段全程约18 min。列车最高时速80 km，平均时速为30 km(含停靠时间)。此前，福州地铁公司通过地铁沿线周边街道、社区以及网络平台派发试乘券。据悉，福州地铁将于5月18日投入试运营，正式对外售票，1号线运营时间为6：30至21：30，还将推出一卡通、月票、年票等优惠便民措施。

(摘自2016年5月13日人民网，记者 吴隆重、谢曦报道)

Temperature Buckling Deformation of the Embedded Track Slab in Tramcar System

YI Xin, YANG Gang,LIU Guangsheng

To study the effect of temperature variation on the temperature gradient and the buckling deformation of embedded track slab within 24 hours, a good track-laying that covers 200 mm greening soil slab is selected. According to the field test, theoretical method and finite element numerical method are used to calculate the slab warping displacement, and provide reference for the structural design of embedded track. The results show that within an observation of 24 hours, the performance of the slab displays substantially a positive temperature gradient, the maximum positive temperature gradient is 10.4 ℃/m, and the maximum warping deformations of slab is 0.0280 mm. Through theoretical calculation and numerical computation, the maximum warping displacement is measured as 0.019 4 mm and 0.027 0 mm respectively, both are close to the results of field measurement. Thus the rationality and reliability of the measured temperature data and the finite element model are verified.

tramcar; embedded track; temperature gradient; buckling deformation

U 213.2+42：U 482.1

10.16037/j.1007-869x.2016.06.020

2014-08-13)