无黏结部分预应力砼梁恢复力模型的研究

唐昌辉,倪 佳,程明慧

(湖南大学 土木工程学院，湖南 长沙 410082)



无黏结部分预应力砼梁恢复力模型的研究

唐昌辉†,倪 佳,程明慧

(湖南大学 土木工程学院，湖南 长沙 410082)

基于OpenSEES软件的二次开发平台，对无黏结部分预应力混凝土梁的截面恢复力模型进行了研究.根据试验统计和理论分析，建立了无黏结部分预应力混凝土梁的截面弯矩-曲率滞回模型，并通过编制Visual C++程序，将其植入到OpenSEES软件的材料子类中，用于无黏结部分预应力混凝土结构的非线性计算，分析过程中无需迭代计算无黏结预应力筋的应力增量，解决了无黏结部分预应力混凝土结构受力分析的关键问题.利用OpenSEES软件，基于已建立的无黏结部分预应力混凝土梁的截面恢复力模型，选用基于柔度法的非线性梁柱单元，采用位移控制，计算了低周反复荷载作用下无黏结部分预应力混凝土梁的弯矩-挠度滞回曲线，计算曲线与试验曲线吻合良好，说明已建立的无黏结部分预应力混凝土梁的截面恢复力模型的可靠性，为无黏结部分预应力混凝土结构的非线性计算提供了理论依据.

无黏结部分预应力砼梁；低周反复荷载；OpenSEES；恢复力模型；弯矩-挠度滞回曲线

无黏结预应力砼梁的恢复力模型研究一直是工程界和学术界共同关注的问题.杜拱辰[1]基于材料的本构模型，采用弯矩-曲率分析方法，假定无黏结筋长度的增长与周围砼长度变化总和相等，不断迭代求解无黏结预应力筋的极限应力，该方法在计算破坏状态情况下是可以实现，但对于无黏结预应力砼梁在其他受力状态就难以实现，不能求得无黏结预应力砼梁的弯矩-挠度滞回曲线；唐昌辉等人[2-3]选用弯矩-曲率分析方法，将梁划分为更为精细的N段，基于材料的本构关系，通过迭代梁的挠曲线和无黏结预应力筋的合力，求解梁的跨中弯矩-挠度曲线，该方法的优点是可以计算无黏结预应力砼梁的受力全过程弯矩-挠度滞回曲线.上述方法均需进行无黏结预应力筋的应力增量的迭代计算，计算程序编制较为复杂.此外，唐昌辉[4]等人根据试验弯矩-曲率拟合曲线，提出了无黏结预应力砼梁的截面恢复力模型，并基于截面恢复力模型，通过虚梁法，分级加曲率求解梁的跨中弯矩-挠度曲线，该方法无需迭代计算无黏结预应力筋的应力增量，且能较准确求得无黏结预应力砼梁的受力全过程弯矩-挠度滞回曲线，但计算程序受截面形式、配筋等参数的制约，不具有重用性，每次计算需根据具体的结构参数重新编程.

根据试验结果和平衡条件，可得到梁的骨架曲线特征点，并利用OpenSEES软件开源的特点，编制了Visual C++程序，将截面弯矩-曲率滞回模型植入到OpenSEE二次开发平台中，计算了无黏结预应力砼梁在低周反复荷载作用下的弯矩-挠度滞回曲线.此方法无需迭代计算无黏结预应力筋的应力增量，同时利用OpenSEES面向对象的程序设计的优势，实现程序的重用性.用户可基于OpenSEES平台建立所需的有限元模型，并调用植入的截面恢复力模型的命令，进行无黏结预应力砼结构的非线性分析，为OpenSEES解决无黏结预应力砼结构恢复力模型的研究提供了一条新的途径.

1 无黏结部分预应力砼梁的截面恢复力模型

已有试验结果表明，无黏结部分预应力混凝土梁的弯矩-曲率滞回曲线，除了具有明显的开裂、屈服、破坏等特征外，还具有压弯构件的滑移、捏缩现象，因此，文献[4]建立了包含骨架曲线和滞回特性的截面弯矩-曲率恢复力模型，如图1所示.

图1 无黏结部分预应力砼梁的截面恢复力模型Fig.1 Restoring force model of unbounded partially prestressed concrete beam

1.1 骨架曲线的确定

基本假定：

1)除预应力筋应变外，钢筋混凝土截面满足平截面假定；

2)截面开裂后忽略受拉区混凝土的抗拉作用；

3)非预应力筋屈服前，混凝土与非预应力筋处于弹性阶段，其应力-应变关系服从虎克定律；

4)无黏结预应力筋与混凝土之间无摩擦；

5)极限承载力计算时，受压区混凝土的应力图形可按《混凝土结构设计规范》(GB 50010-2010)[5]简化为等效的矩形应力图.

开裂点A(D)：

对照《无黏结预应力混凝土结构技术规程》(JGJ92)[6]，对称布置无黏结预应力混凝土梁的开裂弯矩如式(1)所示，考虑截面塑性变形，取截面刚度为0.85EcI0，开裂点曲率如式(2)所示：

(1)

(2)

式中：σpc为扣除预应力损失后，由预加力在抗裂验算边缘产生的混凝土预压应力；γ为截面塑性矩系数．

屈服点B(E)：

由平衡条件可得，

(3)

从中求得ξy，再对受压区预应力筋合力作用点取矩得到屈服弯矩的表达式如下：

(4)

截面的屈服曲率为：

(5)

极限点C(F)：

由平衡条件可得，

(6)

从中求得ξu，再对受压区预应力筋合力作用点取矩得到极限弯矩的表达式如下：

(7)

截面的极限曲率为：

(8)

如图1所示，截面加载超过极限点，进入负刚度阶段，点T(G)的弯矩和曲率分别为：

(9)

另取kCT=-0.08Mcr/φcr，即

(10)

1.2 滞回规则特征点的确定

正(反)向定点R(M)的确定：

试验数据表明，正(反)向定点弯矩的绝对值随综合配筋指标q0的增大而减小，通过回归分析得到正(反)向定点弯矩的表达式:

(11)

正(反)向定点对应的曲率大致与屈服点曲率相等，即正(反)向定点的曲率:

(12)

正(反)向捏拢点L(Q)的确定:

同样对已有试验数据进行拟合分析，得到正(反)向捏拢点弯矩的表达式:

(13)

正(反)向捏拢点曲率的表达式：

(14)

2 基于OpenSEES截面恢复力模型的程序实现

2.1 程序实现

根据OpenSEES的软件架构[7-10]，若将截面恢复力模型植入到Open SEES二次平台中，只需在Material类基础上派生出新的材料子类.Material类有3个派生的子类：Uniaxial Material类、NDMaterial类、Section Force Deformation类.其中，Uniaxial Material类用于定义一维材料模型，包括纤维截面的应力-应变曲线和单元截面的力-变形曲线；NDMaterial类用于定义多维材料模型，如，实体单元的应力-应变响应；Section Force Deformation类同样用于定义多维材料模型，如，压弯构件的力-变形关系或零单元的弯曲和剪切本构关系的合成应力.

本文基于UniaxialMaterial类派生出UPCMaterial类，通过编译C++程序，植入对称布置无黏结部分预应力混凝土梁的截面恢复力模型：1)利用派生类的函数成员覆盖基类的函数成员，并定义恢复力模型的构造函数和私有变量，创建代码文件UPC Material.h；2)通过编写恢复力模型的骨架曲线与滞回规则，实现头文件中的函数成员，创建代码文件UPCMaterial.cpp；3)基于VS2010编译平台，将创建的代码文件和其它类文件载入UPC Material项目，生成UPC Material工程和动态链接库文件UPCMaterial.dll，并将其与结构分析的Tcl命令流放到一个子目录中；4)在OpenSEES中仅需通过Tcl命令流调用已经植入的UPCMaterial材料，进行结构的非线性分析计算.

Tcl命令流具体如下：

uniaxialMaterial UPCmaterial $matTag $mom1p $rot1p $mom2p $rot2p $mom3p $rot3p $mom4p $rot4p $momR $rotR $TmomL $mom1n $rot1n $mom2n $rot2n $mom3n $rot3n $mom4n $rot4n $momM $rotM $TmomQ $q0；

$matTag为材料标号；

$mom1p $rot1p为骨架曲线上正向开裂点的弯矩和曲率；

$mom2p $rot2p为骨架曲线上正向屈服点的弯矩和曲率；

$mom3p $rot3p为骨架曲线上正向极限点的弯矩和曲率；

$mom4p $rot4p为正向骨架曲线考虑截面进入负刚度的弯矩和曲率；

$momR $rotR为正向定点的弯矩和曲率；

$TmomL为正向捏拢点的弯矩；

$mom1n $rot1n为骨架曲线上反向开裂点的弯矩和曲率；

$mom2n $rot2n为骨架曲线上反向屈服点的弯矩和曲率；

$mom3n $rot3n为骨架曲线上反向极限点的弯矩和曲率；

$mom4n $rot4n为反向骨架曲线考虑截面进入负刚度的弯矩和曲率；

$momM $rotM为反向定点的弯矩和曲率；

$TmomQ为反向捏拢点的弯矩；

$q0为截面的综合配筋指标 ．

2.2 弯矩-挠度曲线的确定

与文献[4]的拟梁法不同,本文基于OpenSEES平台，选用基于柔度法的非线性梁柱单元，且采用位移控制，模拟试验梁在低周反复荷载试验的弯矩-挠度滞回曲线.通过分级增加跨中挠度，得到当前结构位移下的单元变形和截面变形，再根据截面恢复力模型，得到相应的截面柔度矩阵和截面抵抗力；通过单元内部迭代，不断消除截面的不平衡力和单元的残余变形，可得到单元刚度矩阵和结构刚度矩阵，从而求得当前跨中挠度所对应的荷载大小.具体过程如图2所示[9-12].

3 基于截面恢复力模型的无黏结预应力砼梁数值模拟

3.1 试验简介

本文选取唐昌辉[4]的2根对称布置无黏结部分预应力混凝土梁和MUGURUMA H的无黏结部分预应力混凝土梁进行数值模拟.试验梁的基本数据如表1所示，试验梁的配筋如图3所示.

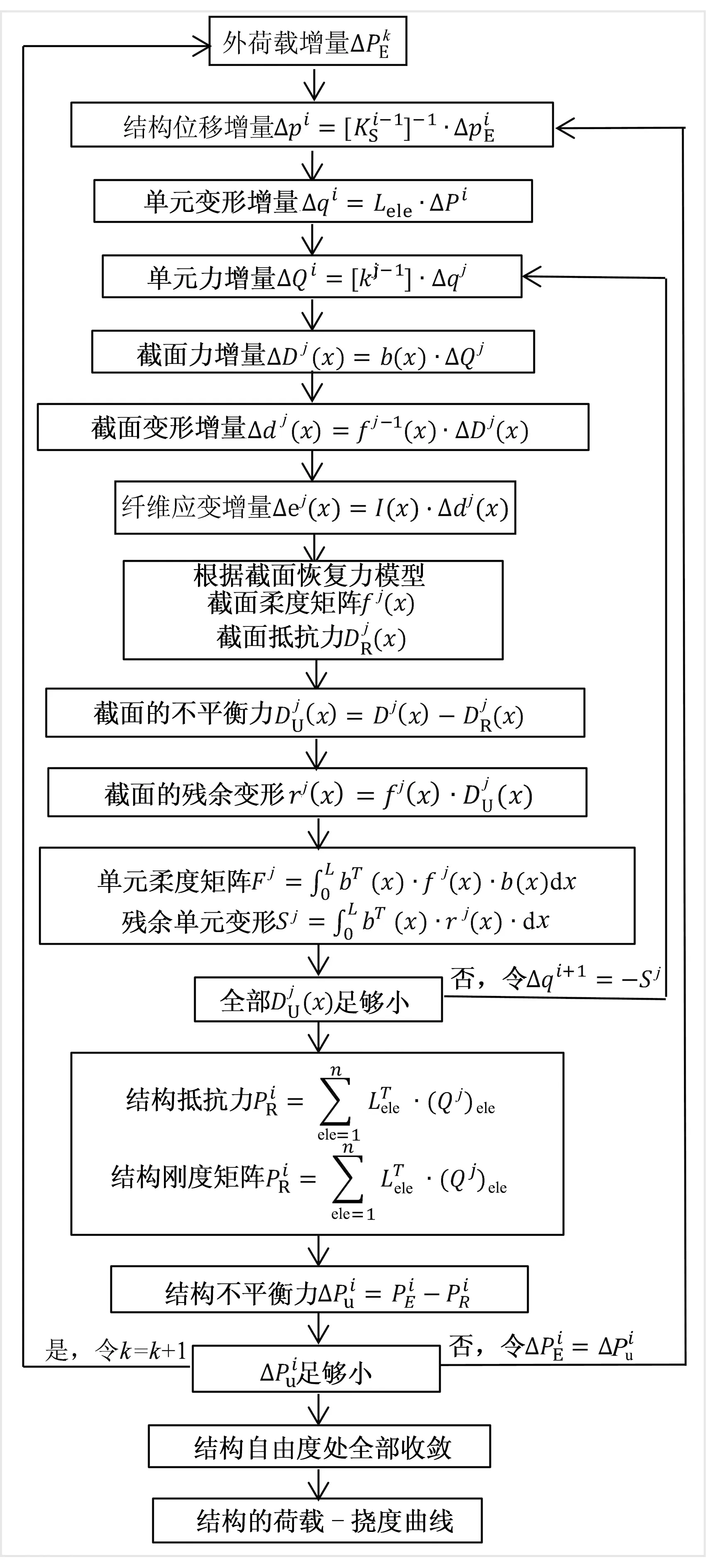
图2 计算框图Fig.2 Calculating frame表1 试验梁的基本数据Tab.1 Main parameters of tested beam

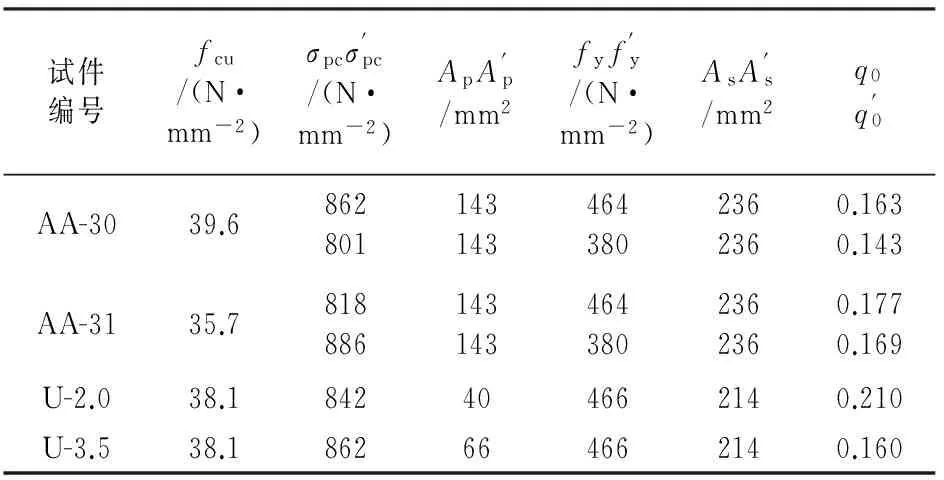
试件编号fcu/(N·mm-2)σpcσ'pc/(N·mm-2)ApA'p/mm2fyf'y/(N·mm-2)AsA's/mm2q0q'0AA-3039.68628011431434643802362360.1630.143AA-3135.78188861431434643802362360.1770.169U-2.038.1842404662140.210U-3.538.1862664662140.160

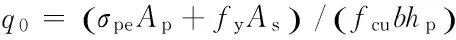
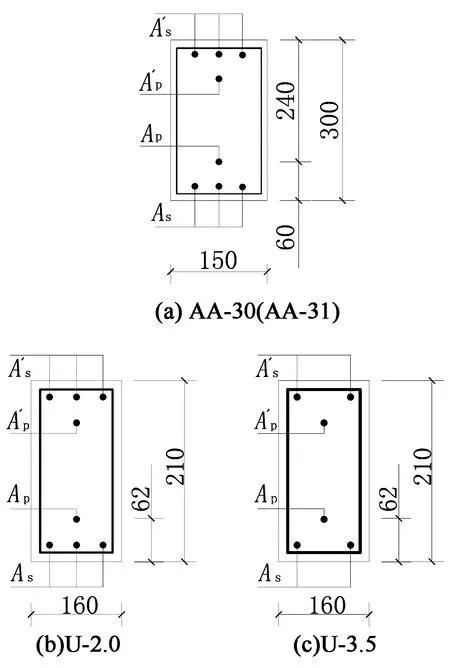
图3 试验梁配筋图Fig.3 Reinforcement of tested beam

3.2 数值模拟结果

无黏结部分预应力砼梁选用基于柔度法的非线性梁柱单元，其单元截面特性选用基于上述恢复力模型的截面定义，非线性分析同样分为2个荷载工况，第1种工况为力控制加载，将预应力作用和自重施加到结构上，计算结构的初始应变；第2工况为位移控制加载，以跨中节点为控制节点，进行往复加载、卸载、反向加载，以模拟低周反复荷载试验，模拟结果如图4所示.

从图中可以看出，计算的弯矩-挠度滞回曲线与试验曲线较吻合.与基于材料本构模型相比，基于截面恢复力模型对结构进行非线性分析无需进行截面积分，可直接由恢复力模型得到截面柔度矩阵，兼顾了非线性计算的效率和精度.

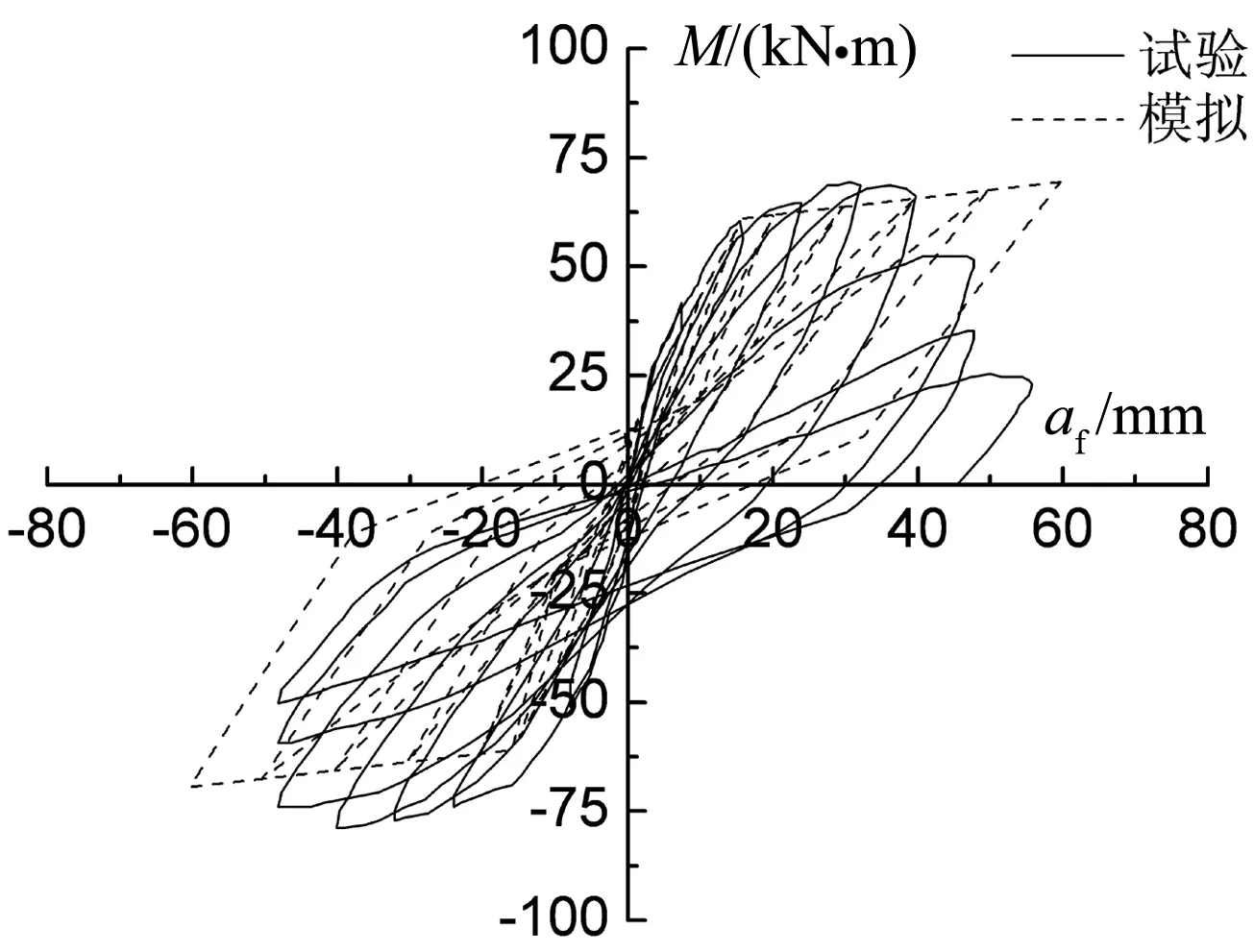
(a)AA-30

(b)AA-31

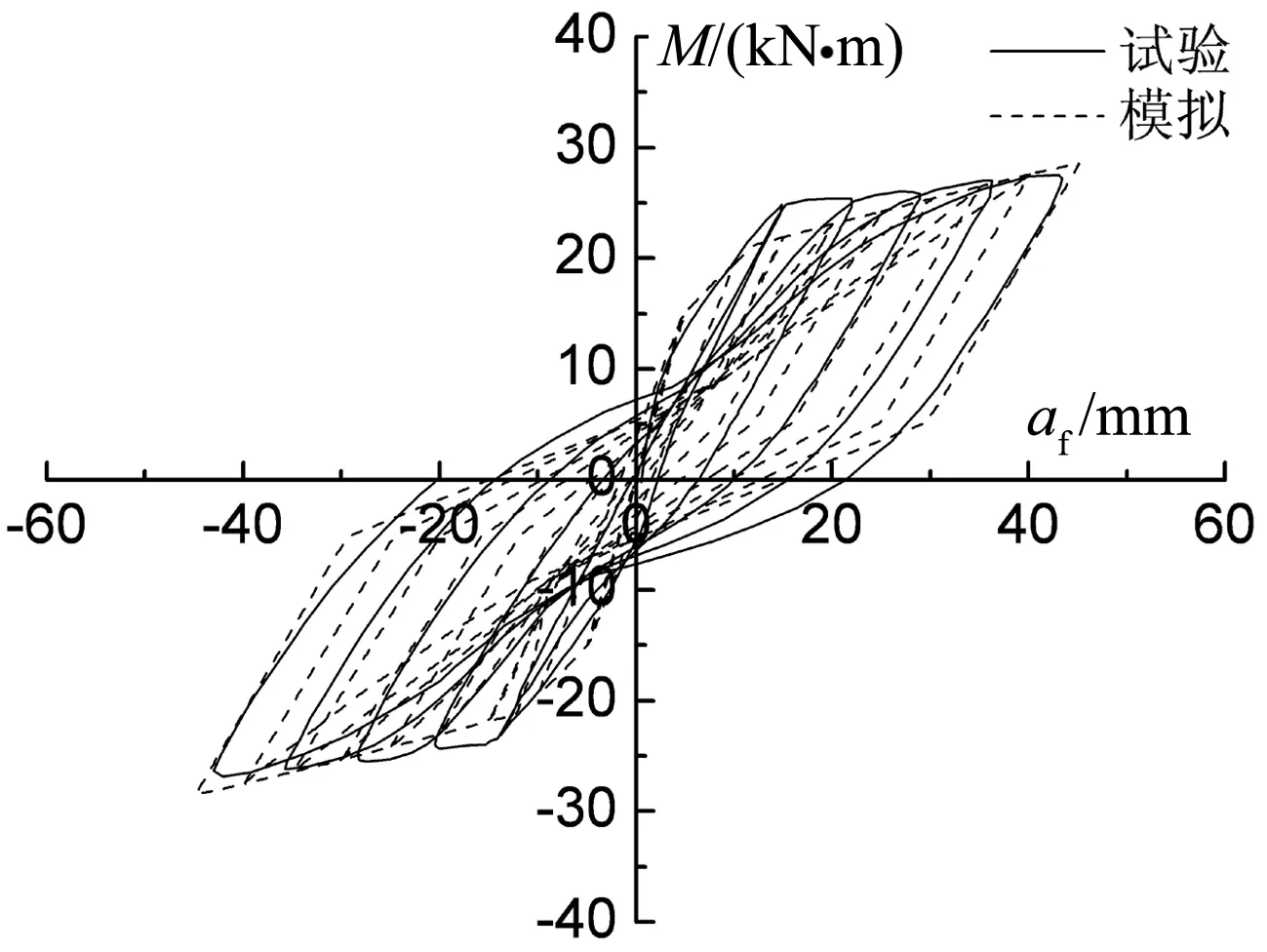
(c)U-2.0

(d)U-3.5图4 基于截面恢复力模型的弯矩-挠度滞回曲线Fig.4 Moment-deflection hysteretic curves based on restoring force model of section

4 结 论

1)利用OpenSEES开源的特点，植入了无黏结预应力筋的截面弯矩-曲率恢复力模型，利用OpenSEES中基于柔度法的非线性梁柱单元，对无黏结预应力砼梁的恢复力模型进行了研究，获取了基于OpenSEES解决无黏结预应力砼结构恢复力模型的一种新方法.

2)计算了4根无黏结预应力砼结构梁的弯矩-挠度滞回曲线，与试验曲线比较，结果吻合较好，验证了二次开发程序的可靠性.由于截面柔度矩阵可直接求得，无需截面积分，兼顾了非线性计算的效率和精度.

[1] 杜拱辰.部分预应力混凝土[M].北京:中国建筑工业出版社,1990:89-94.

DU Gong-chen. Partial prestressed concrete [M]. Beijing: China Architecture and Building Press,1990:89-94. (In Chinese)

[2] 唐昌辉,倪佳,叶林. 无黏结部分预应力混凝土梁非线性全过程滞回分析[J].湖南大学学报：自然科学版,2015,42(7):62-68.

TANG Chang-hui, NI Jia, YE Lin. Nonlinear full range hysteretic analysis on unbonded partically prestressed concrete beams[J]. Journal of Hunan University: Natural Sciences,2015,42(7):62-68.(In Chinese)

[3] 唐昌辉,易伟建,沈蒲生. 无黏结筋对构件抗弯刚度的贡献分析与研究[J].湖南大学学报：自然科学版,2001,28(5):75-79．

TANG Chang-hui, YI Wei-jian, SHEN Pu-sheng. The contribution to the flexural stiffness of the unbounded tendons in prestressed concrete beams[J]. Journal of Hunan University: Natural Sciences, 2001,28(5):75-79. (In Chinese)

[4] 唐昌辉,刘冬明,李雲. 对称布置无黏结预应力混凝土梁恢复力模型研究[J].建筑结构,2015,45(4):68-72.

TANG Chang-hui, LIU Dong-min, LI Yun. Research on restoring force model of unbonded partically prestressed concrete beams with symmetrical tendons[J]. Building Structure,2015,45(4):68-72.(In Chinese)

[5] GB50010-2010 混凝土结构设计规范[S]. 北京:中国建筑工业出版社,2010:37-38.

GB50010-2010 Code for design of concrete structures[S]. Beijing: China Architecture and Building Press, 2010: 37-38. (In Chinese)

[6] JGJ92-2004无黏结预应力混凝土结构技术规程[S]. 北京:中国建筑工业出版社,1993:13-23．

JGJ92-2004 Technical specification for concrete structures prestressed with unbounded tendons[S]. Beijing: China Architecture and Building Press, 1993: 13-23. (In Chinese)

[7] SCOTT M H, FENVES G L. How to introduce a new material into OpenSees[R]. Berkeley:PEER, University of California, Berkeley, 2001:1-23．

[8] MCKENNA F T. Object-oriented finite element programming: frameworks for analysis, algorithms and parallel computing[D]. Berkeley: University of California, Berkeley, College of Engineering,1997:11-45．

[9] FILIPPOU F C, TAUCER F F, SPACONE E. A fiber beam-column element for seismic response analysis of reinforced concrete structures[R]. Berkeley: Earthquake Engineering Research Center, College of Engineering, University of California, Berkeley, 1991:23-88.

[10]陈学伟,林哲.结构非线性程序OpenSEES原理与实例[M].北京:中国建筑工业出版社,2014:15-36.

CHEN Xue-wei, LIN Zhe. Structural nonlinear analysis program OpenSEES theory and tutorial[M]. Beijing: China Architecture and Building Press, 2014:15-36. (In Chinese)

[11]陈学伟,韩小雷,孙思为.三种非线性梁柱单元的研究及单元开发[J].工程力学,2011,28(S1):5-11.

CHEN Xue-wei, HAN Xiao-lei, SUN Si-wei. Research and development of three nonlinear beam-column elements[J]. Engineering Mechanics,2011,28(S1):5-11. (In Chinese)

[12]MUGURUMA H. Study on low-cycle fatigue strength of post-tensioned unbonded prestressed concrete beams[J]. CEB Bulletin D’information,1979,381-384.(In Japanese)

Research on Restoring Force Model of Unbonded Partially Prestressed Concrete Beams

TANG Chang-hui†, NI Jia，CHENG Ming-hui

(College of Civil Engineering, Hunan Univ, Changsha, Hunan 410082, China)

Based on the secondary development platform of OpenSEES software, this paper studied the restoring force model of unbonded partially prestressed concrete beam sections. According to the statistics of experiments and theoretical analysis, the moment-curvature hysteretic model of the section for unbonded partially prestressed concrete beams was established, and planted into Material class in the software of OpenSEES by compiling Visual C++ programs, which is used for the nonlinear analysis of unbonded partially prestressed concrete structure without iterative calculation of stress increment for unbonded prestressed tendon. The crucial problem of stress analysis for unbonded partially prestressed concrete structure was then solved. Moreover, under displacement control, this paper considered the nonlinear beam-column element based on flexibility to calculate the moment-deflection hysteretic curves of unbonded partially prestressed concrete beams under low cyclic reversed loading on the basis of established restoring force model. The calculation results are reasonably identical to experiment results, which indicates the reliability of established restoring force model, and provides theoretical basis for the nonlinear analysis of unbonded partially prestressed concrete structures.

unbonded partially prestressed concrete beams; low cyclic reversed loading; OpenSEES; restoring force model; moment-deflection hysteretic curves

1674-2974(2016)11-0055-06

2015-11-23

国家自然科学基金资助项目(51278179), National Natural Science Foundation of China(51278179)

唐昌辉(1964-)，男，湖南新宁人，湖南大学副教授，博士†通讯联系人，E-mail: tchui2010@126.com

TU378.2

A