基于二重切比雪夫多项式的多自由度系统SMA非线性恢复力识别
2014-09-08辛璐璐
许 斌,辛璐璐,贺 佳
(1.湖南大学 土木工程学院,长沙 410082; 2. 湖南大学 建筑安全与节能教育部重点实验室,长沙 410082;3.香港理工大学 土木与环境工程系,香港九龙)
工程结构在地震等强动力荷载作用下损伤识别及性能评估是灾后救援、恢复重建中关键。结构损伤识别方法大多基于结构振动测量及特征值或特征向量抽取,通过对结构刚度识别描述结构损伤[1-3]。现有研究表明,基于振动测量的结构参数、损伤识别方法存在对结构小损伤不敏感、特征值受环境因素影响等诸多问题。传统基于模态分析的识别理论基本假设结构处于线弹性阶段,此对损伤缓慢变化的结构可以使用,但对在地震等强动力荷载下结构损伤识别因构件进入非线性状态该方法不再适用。
非线性动力系统识别中非线性恢复力作为系统非线性特性及强弱程度指标颇受关注。较通过识别刚度描述结构在动力荷载作用下损伤,结构构件的非线性恢复力不仅可直观刻画其在振动中进入非线性过程,且可通过非线性恢复力定量描述构件耗能,为损伤评估提供新的手段。但实际土木工程结构在地震作用下,不同构件恢复力模型较难事先用理想的参数化模型准确描述。因此,研究动力荷载作用下能有效识别结构非线性恢复力行为方法具有重要意义。
对非线性动力系统识别,由于结构非线性行为个体差异大,研究远未达到像线性系统的完善程度。Masri等[4]提出的恢复力曲面法(Restoring Force Surface Method)广受关注[5-7]。Mohammad等[8]提出的完全基于激励、响应的直接参数识别法,已实现非线性系统质量、刚度、阻尼等参数的有效识别。许斌等[9-11]基于等价线性思想对多自由系统非线性恢复力进行识别,并基于幂级数多项式模型表征系统恢复力,实现非参数化结构非线性行为识别。该方法无需获知非线性恢复力参数化模型,通过在多自由度系统中引入具有非线性恢复力特性的形状记忆合金阻尼器(MR)进行识别,通过数值模拟及实验数据对识别结构中MR非线性恢复力的可行性进行验证。He等[12]研究部分输入未知时基于幂多项式的结构非线性恢复力及外荷载识别方法。樊建修[13]通过算例探讨Taylor多项式、有理分式、切比雪夫多项式等常用最佳逼近表达式,算例结果表明,与其它逼近式相比,切比雪夫多项式具有精度高、误差分布均匀等优点。
与上述研究不同,本文提出基于二重切比雪夫多项式模型的多自由度结构非线性恢复力识别方法,在结构质量信息及非线性参数化模型完全未知情况下实现多自由度系统非线性恢复力识别。介绍结构各自由度及部分自由度受外激励两种情况下识别方法的具体实现步骤;通过在线性结构数值模型中引入具有理想双旗形非线性恢复力模型的形状记忆合金(Shape Memory Alloy, SMA)阻尼器模拟非线性恢复力,对该非线性多自由度系统恢复力进行识别,探讨不同激励方式下该方法的可行性、抗噪性,并将识别结果与基于幂级数多项式方法进行对比,结果表明,本文方法识别精度更高;对安装SMA阻尼器的多层框架结构模型进行动力实验,用实测激励及动力响应时间序列识别SMA阻尼器恢复力,并与试验值对比。结果表明,基于二重切比雪夫多项式模型的非线性恢复力识别方法能有效识别出动力荷载作用下多自由度系统非线性恢复力及结构质量分布。该方法可用于结构在强动力荷载作用下损伤发生、发展过程的监测及耗能定量评估。
1 基于二重切比雪夫多项式的多自由度体系非线性恢复力时域识别方法
1.1 完整激励下非线性恢复力识别方法
多自由度非线性系统在外激励P(t)作用下的动力平衡方程可表示为

(1)
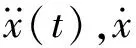
用二重切比雪夫多项式模型描述的非线性恢复力表达式为
(2)

(3)
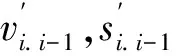
(4)
(5)
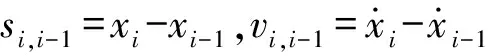
对n个自由度的非线性体系,基于二重切比雪夫多项式模型将式(1)离散为n个方程的线性方程组为
(6)
切比雪夫多项式第一项T0(*)=1,二重切比雪夫多项式模型(式(2))每两个相邻自由度间恢复力切比雪夫表达式中总有数字1项,式(6)中第i个自由度的平衡方程中会出现两个数字1项,因此,不能直接利用最小二乘算法对多项式模型中系数进行识别。由于第n个自由度的方程中只有1个层间恢复力模型,即只有数字1项,故利用最小二乘优化算法识别该体系第n个自由度各系数,再用相邻两自由度间恢复力大小相等方向相反关系对其它自由度的非线性恢复力进行识别:
(7)
(8)
基于式(8)等号右端恢复力识别结果及第n-1自由度的激励及响应时程,利用最小二乘算法可识别该自由度的恢复力及对应质量。依此类推,式(6)中各系数均能得到识别,进而可得基于二重切比雪夫多项式模型的体系非线性恢复力。
1.2 非完整激励下非线性恢复力识别方法
实际工程损伤识别中,尤其大型复杂工程结构,较难对结构全部自由度进行激励。因此须研究非完整激励的损伤识别方法。在非完整激励条件下,设第n个自由度未作用外激励,则
(9)
以两自由度体系为例,设外激励仅作用第1个自由度上,平衡方程为
(10)
据式(7)、(9)可知
(11)
第1个自由度平衡方程可表示为
(12)
基于结构外激励及响应信息可识别式(12)中结构质量及二重切比雪夫多项式各系数。识别体系非线性恢复力模型各系数表达式为。
(13)
至此,两自由度结构基于二重切比雪夫多项式模型的非线性恢复力及结构质量分布均已得以识别。由于系统总非线性恢复力在实际工程中难以测量,故本文通过引入具有非线性恢复力特性的SMA模拟非线性恢复力。实验中由SMA提供的非线性恢复力由力传感器测量获得。为进行识别结果比较,在识别的非线性体系总非线性恢复力中扣除体系本身线弹性恢复力及粘性阻尼力获得SMA提供的非线性恢复力。通过与试验结果比较,验证识别结果的可靠性。此时非线性构件恢复力为
fnon=Rnon[v,s,gnon]-Rlin[v,s,glin]
(14)
式中:fnon为非线性构件提供的恢复力;Rnon[v,s,gnon],Rlin[v,s,glin]为系统中总非线性恢复力、总线性恢复力;v,s为相对速度、相对位移;gnon,glin为总非线性恢复力、总线性恢复的模型系数。
2 SMA非线性恢复力识别的数值模拟验证

图1 计算模型
具有2个集中质量的两自由度体系见图1,每个质点有1个水平自由度,结构第一层安装SMA阻尼器模拟结构非线性特性,各层质量mi=15 kg,线性结构阻尼系数ci=100 N·s/m,层间刚度ki=1.2×105N/m,(i=1, 2)。
SMA具有独特的形状记忆效应、超弹性性能、高阻尼及耐久性耐腐蚀性能好、允许大变形且变形可恢复等优点在建筑结构振动控制领域得到广泛应用[14-15]。SMA具有典型的非线性特性,其本构关系已有不少计算模型[16-17]。本文所用SMA阻尼器双旗形模型见图2。表达式[18]为

(15)
式中:sgn(*)为符号函数;k1=1.0×105N/m为oab,cd段斜率(阻尼器刚度系数);k2=3.0×104N/m为bd,ac段斜率;Sb=0.006 m;Sa=0.5Sb;Sd由动力计算中层间位移最大值决定。
为更好模拟结构非线性恢复力,本文在二重切比雪夫多项式模型(式(2))中取k=q=3。

图2 SMA阻尼器双旗形模型
2.1 完整激励下非线性恢复力识别法数值验证
2.1.1 无噪声影响
不考虑噪声影响,设两组随机激励分别作用于结构两自由度上,荷载作用时间及步长分别取2 s,0.002 s,利用Newmark-ß法计算结构响应。结构激励及各层动力响应时程见图3。

图3 随机激励及结构响应
据各层速度、位移响应计算层间相对速度及位移,再据式(4)、(5)进行数据归一化处理,利用最小二乘优化算法可识别出结构第二自由度对应的质量、模型各系数,结果为
(16)
(17)
(18)
SMA阻尼器提供的恢复力可在识别的体系总非线性恢复力中减去线性结构自身弹性恢复力及结构阻尼作用后获得。各自由度SMA阻尼器提供的非线性恢复力见图4。由图4看出,SMA阻尼器恢复力仅体现在第一层,而第二层SMA阻尼器恢复力趋于零,说明该层无SMA阻尼器,与算例吻合;而SMA阻尼器恢复力值(即理论模型值)与真实值吻合亦较好。表明本文所提基于二重切比雪夫多项式的非线性恢复力识别方法能准确识别结构非线性恢复力。
为与基于幂级数多项式识别法比较,相同激励下基于幂级数多项式模型的SMA阻尼器非线性恢复力识别结果见图5。比较图4、图5看出,本文方法对SMA阻尼器理想双旗形恢复力模型识别精度高,尤其在双旗型模型位移最大点处。两种识别方法识别值与真实值误差定量比较见图6。由图6看出,基于二重切比雪夫多项式模型的非线性恢复力识别结果误差更小。

图4 无噪声影响各层SMA阻尼器恢复力识别结果
2.1.2 6%噪声影响
工程实测中数据易受噪声影响。为验证该方法对噪声的敏感程度,在算例响应信号中加入随机噪声信号,噪声水平取6%。识别的结构质量分布为m1=14.90 kg,m2=15.00 kg,与算例值吻合较好。同时获得结构各层基于二重切比雪夫多项式模型的SMA阻尼器恢复力识别结果,体系第二层SMA阻尼器提供的恢复力趋于零,说明该层未安装SMA阻尼器,与实际情况完全符合。有噪声影响下结构第一层SMA阻尼器恢复力识别值与真实值比较见图7。由图7看出,即使受6%噪声影响,该方法仍能有效识别出结构非线性特性。
2.2 非完整激励下非线性恢复力识别法数值验证
2.2.1 无噪声影响
设仅在图1数值模型的第1自由度上作用一组随机激励,即第2自由度上作用力为零,据Newmark-ß法计算出结构响应。并据式(4)、(5)对动力响应归一化处理,由式(11)、(12)识别出第1自由度对应的平衡方程的各系数为
(19)
由式(19)看出,结构质量识别值为m1=15.00 kg、m2=15.09 kg,与数值模型值吻合良好。据式(2)可得结构第一层基于二重切比雪夫多项式模型的恢复力表达式。据式(13)可进一步识别结构第二层总非线性恢复力表达式。

图7 6%噪声影响下底层SMA阻尼器恢复力识别结果
SMA阻尼器提供恢复力的识别结果见图8。由图8看出,结构第二层SMA阻尼器恢复力几乎为零,说明该层无SMA阻尼器,结构第一层SMA阻尼器恢复力识别值与真实值吻合良好。
2.2.2 6%噪声影响
设在结构响应计算值中加入6%随机噪声,识别出体系的质量分布(m1=14.98 kg,m2=15.10 kg)及各自由度间非线性恢复力。SMA阻尼器提供的恢复力识别结果中结构第二层识别值仍趋于零,而第一层呈明显双旗形特性且与计算值吻合较好,见图9。由图9看出,即使在激励非完整且存在环境噪声情况下,该方法仍能较好识别出体系的非线性特性位置并对非线性恢复力进行定量识别。
为更直观描述本文方法对系统非线性行为的识别效果,不同激励条件、噪声水平下SMA阻尼器恢复力识别值与真实值相对误差见表1。由表1看出,识别SMA阻尼器恢复力相对误差均在1%以内,表明该方法的可行性及对测量噪声的鲁棒性。

表1 数值模拟验证SMA阻尼器恢复力识别误差
3 多自由度结构非线性恢复力识别实验验证
3.1 实验模型及装置

图10 实验结构模型及装置
用非线性结构模型实验验证本文方法的有效性。设计制作四层钢框架模型见图10,SMA阻尼器安装于结构第四层模拟结构非线性特性,见图11。结构模型平面尺寸300 mm×400 mm,层高0.3 m,模型总高1.2 m,结构总质量51.41 kg。结构立柱截面尺寸30 mm×5 mm,楼面板厚10 mm,所有节点均采用螺栓连接。因结构楼板平面内刚度相对较大且模型质量集中在楼板上,可将模型简化为4自由度集中质量。SMA阻尼器丝用直径8 mm的Ti-Ni合金丝,用4个夹具安装于线性模型第四层,其恢复力可由与上层楼板连接的钢板及与下层楼板固定的阻尼器中间支座间力传感器直接测得。在每层楼板均布置加速度传感器,用力锤施加冲击荷载,采样频率1024 Hz,用动态数据采集系统记录结构加速度响应,并对加速度信号用截止频率0.5 Hz的高通滤波处理,结构速度、位移响应由加速度时程积分获得。

图11 SMA阻尼器
3.2 完整激励下非线性恢复力识别法验证
由于试验中所测非线性恢复力仅SMA阻尼器恢复力,进行结果比较时需将线性结构恢复力由总非线性恢复力中扣除,为此先对未安装SMA阻尼器时的线性结构进行动力实验,得线性恢复力为
(20)
式中:si,vi(i=1,2,3,4)为层间相对位移及相对速度。
安装SMA阻尼器后用力锤依次激励非线性结构每一层,其冲击荷载及加速度响应实测值见图12、图13,此处速度、位移响应由加速度响应积分获得。

图12 非线性结构外激励
基于归一化的结构层间相对速度及位移信息,据式(6)、(7)识别获得安装阻尼器后结构质量分布为m1=12.29 kg,m2=12.32 kg,m3=16.35 kg,m4=14.68 kg。可见,由于安装SMA阻尼器,结构第三、四层质量增加,与实际相符。而识别的各层间非线性恢复力因篇幅所限其表达式不再列出。据式(14)可得各层SMA阻尼器提供的恢复力,结果见图14、图15。由图14看出,结构第三层非线性恢复力识别值较小,表明结构第三层无SMA阻尼器,与实际情况相符。第一、二层结果类似。图15为结构第四层SMA阻尼器恢复力识别值与实测值对比,二者在整个时程差值见图16。由图16看出,识别值与实验值吻合较好。为进一步验证SMA阻尼器恢复力识别效果,计算SMA阻尼器耗能值,识别值与实测值分别为56.21 N·mm,61.10 N·mm。因此,在完整激励作用下,基于二重切比雪夫多项式模型的多自由度时域识别方法能对结构中非线性特性进行定位、定量评估。
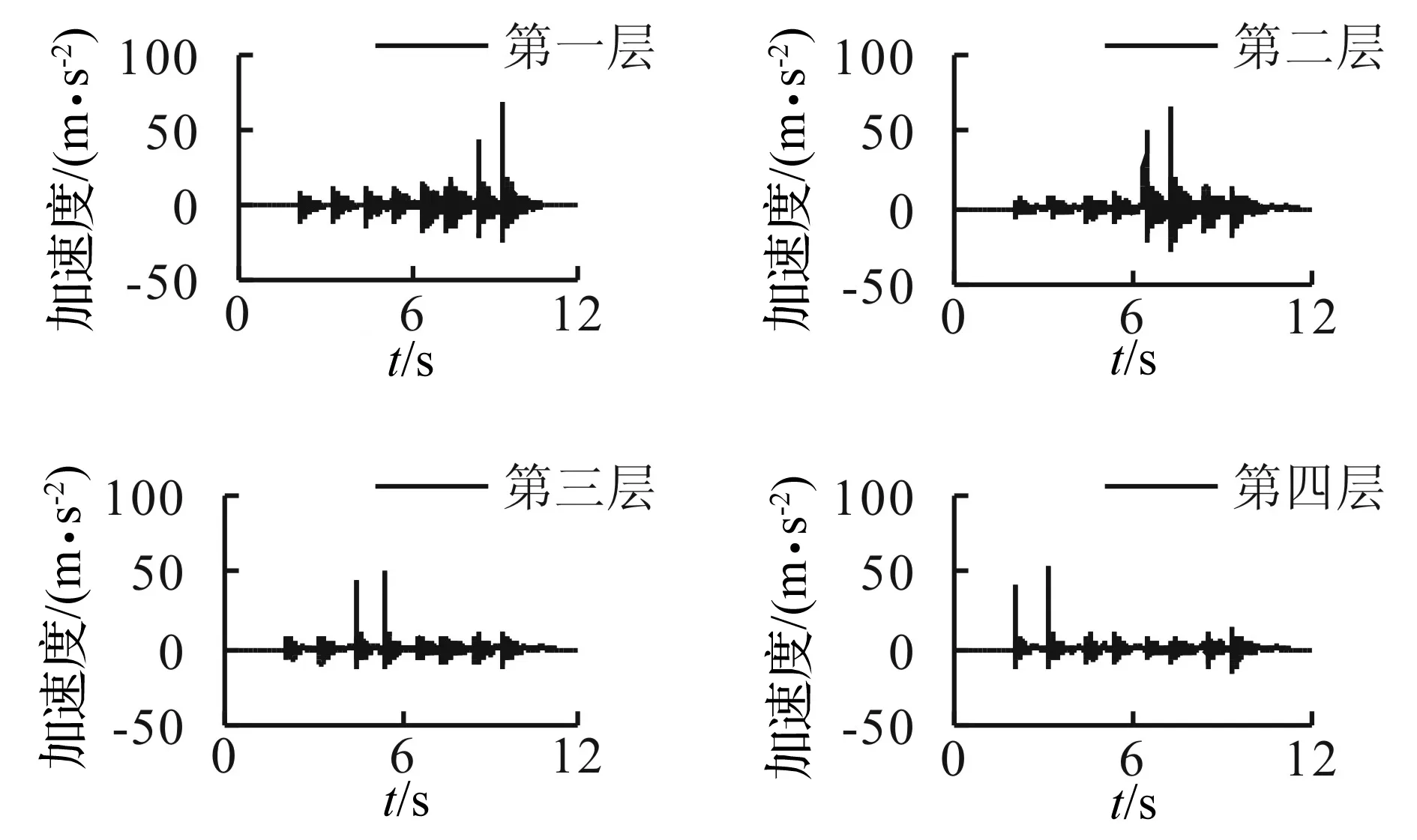
图13 加速度响应实测值

图14 第三层SMA阻尼器恢复力识别值
3.3 非完整激励下非线性恢复力识别法实验验证

图17 加速度响应实测值

图18 第三层SMA阻尼器恢复力识别值
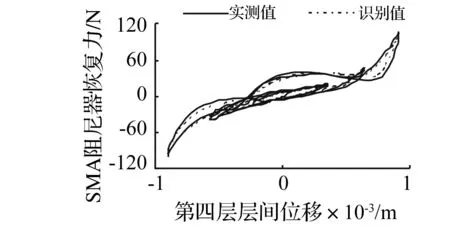
图19 第四层SMA阻尼器恢复力识别结果比较
实验中仅激励结构第三层,采集的结构加速度响应信号见图17。速度、位移响应由实测加速度信号积分获得。识别过程与数值模拟验证。识别出结构第四层至第一层集中质量分别为m4=16.08 kg,m3=17.58 kg,m2=12.63 kg,m1=12.26 kg,结构总质量识别值为58.55 kg,反应出在线性结构中安装阻尼器后质量变化。结构各层非线性恢复力表达式因篇幅限制不再列出。非线性结构各层SMA阻尼器提供的恢复力可由各层间非线性恢复力减去线性恢复力获得。结构第三、四层阻尼器非线性恢复力识别结果见图18、图19。 比较图18、图19看出,结构第三层非线性恢复力结果较小,表明该层无SMA阻尼器,而第四层非线性恢复力较大,表明该层装有SMA阻尼器,与实验相符;通过与SMA阻尼器实测结果对比知,第四层阻尼器提供的非线性恢复力识别结果与实测值仍能较好吻合。据识别的阻尼器非线性恢复力确定阻尼器耗能,第四层SMA阻尼器耗能识别值与实测值分别为39.70 N·mm,44.10 N·mm,两者相对误差在10%以内。该时域识别方法在结构质量未知条件下对结构质量分布及非线性特性识别结果与实测值吻合较好,识别的阻尼器非线性恢复力可用于结构耗能的定量评估。
4 结 论
(1) 本文提出的基于二重切比雪夫多项式模型的多自由度结构中SMA非线性恢复力识别法完全基于结构动力平衡方程,利用优化算法对多自由度结构质量分布及非线性恢复力进行有效识别。探讨在激励完整、非完整两种情况下该识别方法的具体实现过程。
(2) 通过在两自由度数值模型中引入具有双旗形非线性恢复力模型SMA,考虑测量噪声影响,分别在外激励完整、非完整两种工况对该识别方法有效性及抗噪性进行数值验证。通过与基于幂多项式模型识别方法结果比较表明,本文方法识别精度优势明显。
(3) 将SMA阻尼器安装在四层钢框架结构模型中模拟结构非线性行为,通过激励完整、非完整两种荷载下动力实验实测数据验证基于二重切比雪夫多项式模型识别算法的可行性。实验结果表明,该方法能在结构质量未知条件下对实际结构质量分布及结构非线性恢复力进行有效识别。
(4) 本文所提方法能在结构质量及非线性模型完全未知前提下有效识别非线性特性及体系非线性恢复力,为结构在动力荷载作用下损伤行为发生发展过程监测尤其灾后安全评估提供新方法。非线性恢复力识别结果可对结构在动力荷载作用下的耗能进行定量评估。
[1] Patil D P, Maiti S K. Detection of multiple cracks using frequency measurements[J]. Engineering Fracture Mechanics, 2003, 70(12):1553-1572.
[2] Li S Z,Wu Z S. A non-baseline algorithm for damage location in flexural structures using dynamic distributed macro-strain responses[J].Earthquake Engineering and Structural Dynamics,2007,36(9):1109-1125.
[3] Teughels A,Roeck G D.Damage detection and parameter identification by finite element model updating[J].Archives of Computational Methods in Engineering,2005,12(2): 123-164.
[4] Masri S F,Caughey T K. A nonparametric identification technique for nonlinear dynamic problems[J].Journal of Applied Mechanics, 1979,46(2):433-447.
[5] Yar M, Hammond J K. Parameter estimation for hysteretic systems[J]. Journal of Sound and Vibration,1987,117(1):161-172.
[6] Worden K. Data processing and experiment design for the restoring force surface method, part I: integration and differentiation of measured time data[J]. Mechanical Systems and Signal Processing, 1990, 4(4): 295-319.
[7] Worden K. Data processing and experiment design for the restoring force surface method, part II: choice of excitation signal[J]. Mechanical Systems and Signal Processing, 1990, 4(4): 321-344.
[8] Mohammad K S, Worden K, Tomlinson G R. Direct parameter estimation for linear and non-linear structures[J]. Journal of Sound and Vibration, 1992, 152(3):471-499.
[9] 许斌,贺佳. 基于实测时间序列的非线性系统恢复力识别[J].中国工程科学,2011,13(9):76-82.
XU Bin, HE Jia. Nonlinear restoring force identification based on measured time series[J]. Engineering Sciences, 2011,13(9):76-82.
[10] 许斌,贺佳, Sami F.Masri. 动力系统非线性行为识别方法与验证[J].土木工程学报,2011,44(S1):24-30.
XU Bin, HU Jia, Masri S F. Nonlinear behavior identification approach and its validation for dynamic system[J]. China Civil Engineering Journal,2011,44(S1): 24-30.
[11] Xu Bin, He Jia, Masri S F.Data-based identification of nonlinear restoring force under spatially incomplete excitations with power series polynomial model[J]. Nonlinear Dynamics, 2012,67(3):2063-2080.
[12] He Jia, Xu Bin, Masri S F. Restoring force and dynamic loadings identification for a nonlinear chain-like structure with partially unknown excitations[J]. Nonlinear Dynamics, 2012,69(1/2):231-245.
[13] 樊建修.计算机常用函数逼近方法及切比雪夫多项式[J].工业仪表与自动化装置,1986(3):11-18.
FAN Jian-xiu. Function approximation methods and chebyshev polynomial[J].Industrial Instrumentation & Automation,1986(3):11-18.
[14] 薛伟辰,郑乔文,刘振勇,等. 结构振动控制智能材料研究及应用进展[J].地震工程与工程振动,2006,26(5):213-217.
XUE Wei-chen, ZHENG Qiao-wen, LIU Zhen-yong, et al. Developments of research and application of smart materials in controlling structural vibration[J]. Earthquake Engineering and Engineering Vibration,2006,26(5):213- 217.
[15] 吴波,孙科学,李惠,等. 形状记忆合金力学性能的试验研究[J].地震工程与工程振动,1999,19(2):104-111.
WU Bo, SUN Ke-xue, LI Hui, et al. Experimental research on mechanical properties of shape memory alloy[J]. Earthquake Engineering and Engineering Vibration,1999,19(2):104-111.
[16] Liang C, Rogers C A. One-dimensional thermomechanical constitutive relations for shape memory materials[J]. Journal of Intelligent Material Systems and Structures, 1990, 1(2): 207-234.
[17] Auricchio F, Coda A, Reali A, et al. SMA numerical modeling versus experimental results: parameter identification and model prediction capabilities[J]. Journal of Materials Engineering and Performance, 2009, 18(5/6): 649-654.
[18] 李惠,毛晨曦.形状记忆合金(SMA)被动耗能减震体系的设计及参数分析[J].地震工程与工程振动,2001,21(4): 133-139.
LI Hui, MAO Chen-xi. Seismic response of buildings with SMA passive energy dissipation devices: analysis and design[J]. Earthquake Engineering and Engineering Vibration, 2001, 21(4): 133-139.
