基于OpenSees的RC柱拟静力数值分析模型

卜海峰，胡思康，张耀庭，童 康，叶宏伟

(1.华中科技大学 土木工程与力学学院， 湖北 武汉 430074；2.武汉大学 土木建筑工程学院， 湖北 武汉 430070)



基于OpenSees的RC柱拟静力数值分析模型

卜海峰1，胡思康2，张耀庭1，童 康1，叶宏伟1

(1.华中科技大学 土木工程与力学学院， 湖北 武汉 430074；2.武汉大学 土木建筑工程学院， 湖北 武汉 430070)

本文以OpenSees为分析平台，对等位移加载的拟静力试验钢筋混凝土柱进行数值分析。考虑钢筋与混凝土材料本构的选取与搭配、纤维划分、单元划分、积分点数的不同对数值模拟带来的影响，建立合理有效的数值分析模型。分析结果表明：在OpenSees中，选用不同钢筋与混凝土本构模型进行模拟时，计算结果差别较大，且采用不同钢筋与混凝土材料本构进行搭配建模时，对数值模拟的结果也有较大影响；对于钢筋本构，Steel02、ReinforcingSteel模拟效果比Steel01好,且二者分别适应不同的混凝土本构；对于混凝土本构，Concrete01模拟效果最好；纤维截面划分形式对模拟结果有较大影响，平行于作用力方向划分m=1，垂直于作用力方向划分n=10即可满足精度要求；单元数量对模拟结果有一定影响，划分5个已能达较好精度；单元积分点数对模拟结果影响不大，单元取4个积分点时，模型的计算精度已经很高。

钢筋混凝土柱拟静力试验； OpenSees； 本构模型； 纤维模型； 单元积分点数

目前，国内外在钢筋混凝土结构抗震研究上已经取得了较多成果[1]，合理精确地模拟结构在地震作用下复杂的非线性行为表现，是研究结构在地震作用下损伤和破坏机理的关键[2]，有关结构非线性问题的分析模拟，一直是工程结构抗震研究中的重点和难点。结构拟静力试验，是模拟地震时结构在往复振动中的受力和变形时应用最广泛的方法之一[3]。众所周知，真实试件试验的数量毕竟是有限的，数值试验，即数值建模分析已成为了解结构构件复杂受力性能的重要手段，在一定程度上可极大地弥补试验数量上的不足。为此，本文以大型开放式分析软件OpenSees为分析平台，对钢筋混凝土结构构件拟静力试验的模拟分析方法进行研究。试件选用文献[4]钢筋混凝土框架结构拟静力倒塌试验中柱的试验资料，建模时针对OpenSees中不同的钢筋和混凝土本构模型，进行组合搭配，通过与试验结果对比，确定钢筋和混凝土本构相对合理的选择搭配模式；同时，对纤维截面的划分形式、单元数量、单元积分点数等，对数值分析结果的影响进行探讨，为在OpenSees中建立合理有效的钢筋混凝土柱拟静力试验分析模型提供参考。

1 RC边柱拟静力试验简介

RC框架结构拟静力倒塌系列试验详见文献[4～6],本文选取底层边柱试验资料。该柱按照GB 50011-2001《建筑抗震设计规范》，以1∶2缩尺模型设计并配筋，已知混凝土立方体强度fcu,150mm=30.1 MPa，钢筋材料的材性参数如表1所示。柱长850 mm，截面尺寸200 mm×200 mm，底部与混凝土基础整浇，顶部通过千斤顶施加轴压力141 kN，在距柱底750 mm处施加水平力进行拟静力往复加载，先进行荷载控制加载循环3次，随后进行位移控制加载，位移阶段加载制度如图1所示。具体加载装置、各级加载制度及试验结果参见文献[5]，配筋情况参见文献[6]。试验得到的荷载-位移滞回曲线如图2所示，该曲线形状为纺锤形，总体上较为饱满，耗能效果较好。

表1 钢筋材料材性参数

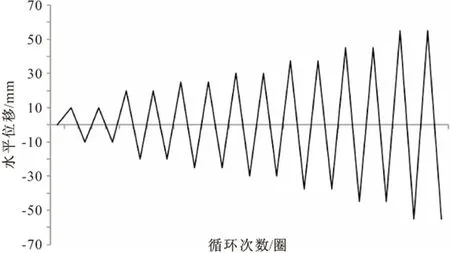
图1 位移控制阶段加载制度

图2 实验柱的滞回曲线

2 数值分析

2.1 初步建立模型

本文以OpenSees为分析平台，截面恢复力模型采用基于柔度法的纤维模型，考虑到钢筋混凝土柱的非线性滞回性能，选择基于位移插值的梁柱单元模型，由于柱子底部约束，考虑钢筋的粘结滑移，认为底部节点处固定，并在该节点处插入零长度单元模型[7]。考虑箍筋的约束作用，将柱子截面分为保护层混凝土和核心区混凝土，保护层厚度定为20 mm，沿局部坐标系下z轴方向划分数为m，沿y轴方向划分数为n，建模时令m=1，n=10，整个截面划分有42个纤维数目，如图3a所示。由于柱子长细比较大，同时根据实验结果，建模时考虑P-Δ效应。

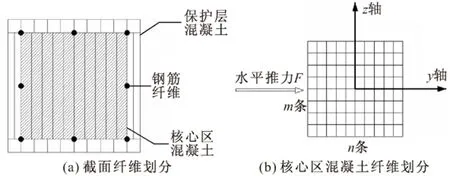
图3 截面纤维模型

2.2 材料本构关系组合的讨论

2.2.1 混凝土本构模型

OpenSees中混凝土材料的研究，刘春燕[3]、陈伟[8]等人已经做了详细介绍，刘立军[9]对核心区混凝土材料本构的选择做了部分研究。OpenSees有Concrete01、Concrete02、Concrete03、Concrete04、Concrete06、 Concrete07等几种混凝土材料(以下分别简称C01、C02、C03、C04、C06、C07)。

这里C01和C02均采用B1akeley[10]推荐的Kent-Scott-Park模型，分三段表示混凝土受压骨架曲线，引入增大系数K以修正箍筋约束对核心区混凝土强度和延性的影响：

ε0=0.002K

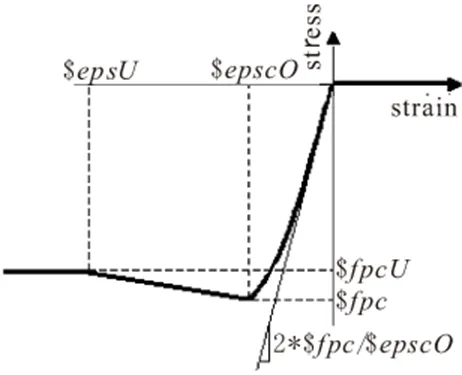
图4 C01控制参数

图5 C01应力-应变滞回关系

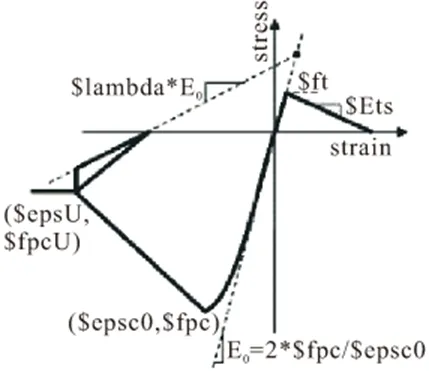
图6 C02控制参数

图7 C02应力-应变滞回关系

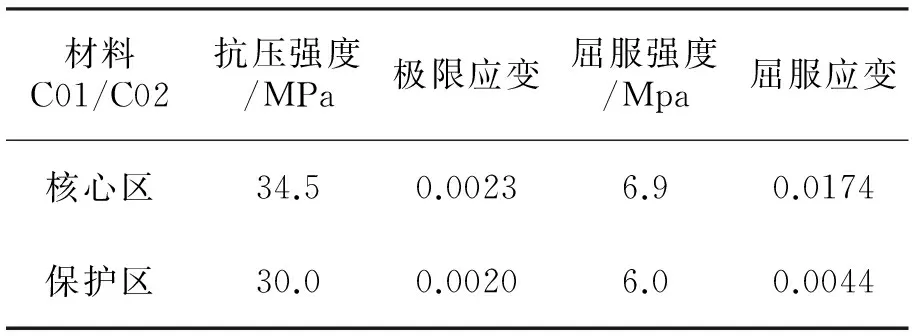
表2 C01和C02受压区段的本构控制参数

C03和C02在受压阶段相同，只在受拉阶段的下降阶段由线性变为非线性，且参数的输入变得复杂，没有C02方便，实用性相对较低，目前较少人使用，这里暂不讨论。

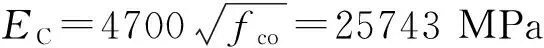
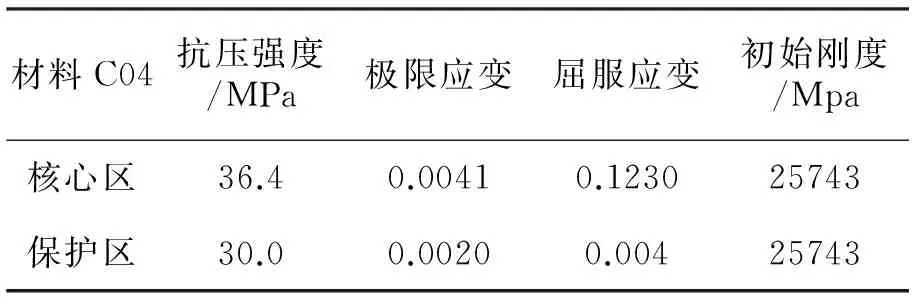
表3 C04受压区段的本构控制参数

C06骨架曲线类似Popovics，滞回规则类似C02，参数的输入也较多。

C07的本构模型是1994年Chang, Mander[17]提出的，其适应性较强，对柱子的形状没有限制，但是参数相对C01和C02较复杂。其本构控制参数如图8所示，滞回规则分三段线描述，如图9所示(具体参数参考文献[18])。参照文献[17]及OpenSees官方说明[18]计算控制参数如表4。

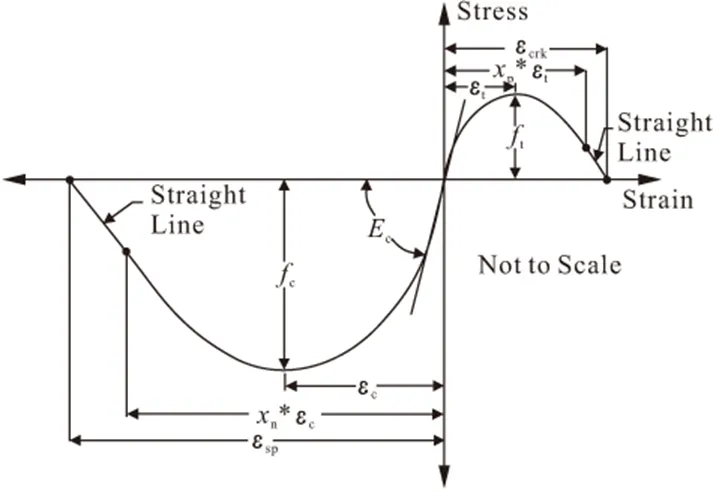
图8 C07控制参数

图9 C07应力-应变滞回规则

表4 C07本构控制参数

2.2.2 钢筋本构模型

钢筋的性能对混凝土柱有很大影响，不同本构模型的模拟结果有较大区别[19]，为了模拟柱子的非线性滞回反应，钢筋采用Steel01,Steel02和ReinforcingSteel三种材料，(以下分别简称S01，S02和SRf)。S01材料的控制参数有屈服强度、弹性模量、应变硬化率，如图10和图11所示。S02控制参数有屈服强度、弹性模量、应变硬化率和三个过度形状控制系数,其数值按照程序推荐使用，参见图12和图13。S01和S02钢材的应变硬化率均取0.6%。

图10 S01本构控制参数

图11 S01等向硬化滞回曲线

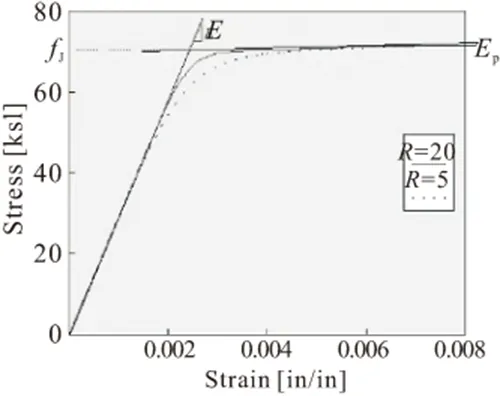
图12 S02本构控制参数

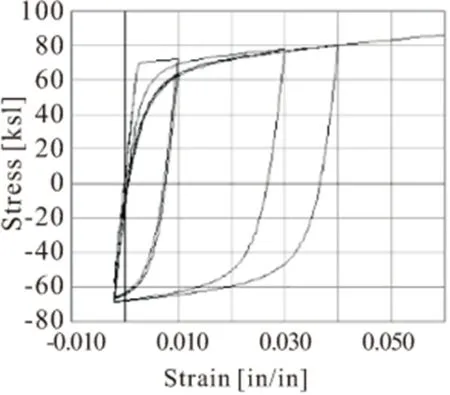
图13 S02等向硬化滞回曲线

SRf是较为精确的模型，但同时比S01和S02复杂，控制参数较多，其钢材骨架曲线分四段描述，分别为线弹性阶段、屈服平台阶段、硬化阶段和最后的软化阶段，控制参数主要有屈服强度、极限强度、初始弹模、初始硬化弹模、初始硬化应变、极限应变等(图14)，滞回性能还可以根据需要调整其它参数。

图14 SRf本构控制参数

2.2.3 数值分析结果与讨论

数值模拟时将以上述5种混凝土本构模型和3种钢筋本构模型分别进行搭配选用，得到15种本构组合：S01+C01、S01+C02、S01+C04、S01+C06、S01+C07(a组图)；S02+C01、S02+C02、S02+C04、S02+C06、S02+C07(b组图)；SRf+C01、SRf+C02、SRf+C04、SRf+C06、SRf+C07(c组图)，其模拟结果与实验结果进行对比，如图15所示：

图15 钢筋本构S01、S02、SRf和混凝土本构C01、C02、C04、C06、C07的15种搭配模拟结果与实验对比

由图15可以看出：

(1)模拟结果的曲线形状与试验曲线接近，水平承载力、刚度退化等模拟效果较好，表明以上15种本构关系搭配模拟的合理性。

(2)15种模拟曲线之间差别仍较大。说明选用不同钢筋与混凝土本构模型进行模拟时，计算结果差别较大。究其原因，不同钢筋和混凝土本构模型的搭配存在选择性，例如Chang, Mander得出C07本构模型时是采用与SRf搭配，C07+SRf模型搭配的模拟曲线与C01+SRf、C02+SRf存在差异，其更接近实验曲线。

(3)对比图15a4、15b4、15c4发现：图15a4中模拟的滞回曲线生硬，反向加载的水平承载力过大，刚度存在突变，曲线不柔和，模拟较差；图15b4、15c4滞回曲线饱满，与试验曲线较吻合。对比图15a1、15b1、15c1；15a3、15b3、15c3；15a5、15b5、15c5可以发现类似现象。说明：S02和SRf模型的模拟效果较好，S01模型相对于S02和SRf模型，模拟效果不够理想。

(4)图15c1、15c2、15c3、15c4、15c5模拟曲线均较饱满，捏合不充分，呈梭形，强度退化趋势一致，总体上模拟效果相同，其中图15c1在本组中模拟效果最好。b组5个图也有一定的共性，其中图15b1拟合效果最好。说明：混凝土本构模型已比较完备且模拟效果相对稳定和精确，其中C01模拟效果最好。

(5)对比图15b2、15c2，图15c2模拟曲线饱满程度与试验接近，水平承载力拟合较好，图15b2误差较大；对比图15b3、15c3，图15b3对水平承载力拟合较好，图15c3模拟效果较差。针对S02与SRf，混凝土本构为C02时，钢筋本构选SRf较好；混凝土本构为C04时，钢筋本构选S02较好。说明：钢筋本构模型在S02与SRf之间选择时，须视具体的混凝土本构模型来确定。仔细对比可知，S02与C01、C04、C07配合使用的效果较好，SRf则与C01、C02、C07配合较好。

(6)图15模拟曲线出现一些不足，对刚度退化过程模拟普遍都存在一定误差，强度和刚度比试验值大，这是由于没有考虑加载后期纵筋屈服。

2.3 纤维截面划分的讨论

在确定材料本构搭配的基础上，讨论模型截面划分对模拟结果的影响。一般认为，纤维划分数达到40左右已经有足够的精度[20]，且核心区混凝土一般按照等向划分[21]，即m=n，此次选用S02+C01本构搭配，柱的加载方向为整体坐标系的x方向，根据OpenSees坐标变换规则，即截面局部坐标系下的y方向，如图3b所示。现考虑核心区混凝土划分数量的影响。

将核心区y方向依次划分为n=2，4，6，8，10，12，z方向均为m=1，得到柱底剪力-加载点位移关系曲线如图16所示。对比发现，初始n=2和n=4两条线差异较大，主要由于纤维划分过少导致精度不够，误差较大，同时研究表明，混凝土材料C01本构关系软化阶段对模拟结果也产生了一定影响[22]。随着划分数量的增加，4条以后曲线差异逐渐减小，到12条时已趋于稳定，建模时截面划分n=10即能满足精度要求。

将核心区z方向依次划分为m=2，4，6，8，10，12，y方向均为n=10，模拟的滞回曲线并没有任何变化，如图15b1所示。

显然截面纤维划分不仅与截面形式有关，还与水平力加载方向有关，对于单向拟静力加载的RC柱，平行于作用力方向的截面划分对模拟结果无影响。说明：普通多层框架结构中的方形截面RC柱，其单向拟静力加载试验的数值分析，考虑到计算效率，z方向选m=1，y方向选n=10即可满足精度要求。这与通常人们对纤维截面等向划分方式有一定的不同，可以看做纤维等向划分在单向加载特定情况下的简化。

图16 y方向不同划分数柱底剪力-加载点位移关系曲线

2.4 单元及其积分点的讨论

基于位移插值的梁柱单元，其计算精度与单元划分程度及单元积分点数有关[23,24]，通常认为单元和积分点划分越多，分析时间越长，计算精度也越高。

2.4.1 单元划分数量

取m=1,n=10的纤维截面，如图3a所示，单元使用Displacement-Based Beam-Column Element，将柱分别划分为2～6个单元，每个单元均取4个积分点，得到柱底剪力-加载点位移关系曲线如图17所示，可以看出：柱单元数量为2和3时误差较大；超过3后，曲线开始趋于稳定，单元数量为5时曲线已基本稳定。

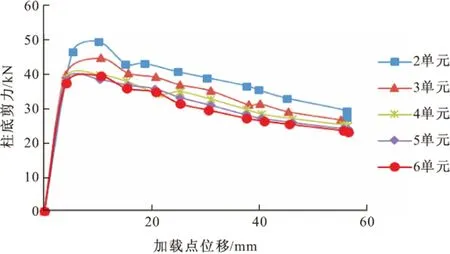
图17 不同单元数量柱底剪力-加载点位移关系曲线

2.4.2 积分控制点划分数量

柱单元数量为5，单元积分点数依次取2～6点，得到柱底剪力-加载点位移关系曲线如图18所示，可以看出：积分点数为2和3时出现轻微波动，3点以上时曲线已稳定。积分点数的选取对精度影响相对不大，在满足要求的情况下，单元取4个积分点，模型计算精度已经较高。

图18 不同积分点数柱底底剪力-加载点位移关系曲线

3 结 论

本文以OpenSees为分析平台，对等位移加载的拟静力试验钢筋混凝土柱进行数值分析，探究钢筋与混凝土材料本构的选取、纤维划分、单元划分、单元积分点数对模拟结果的影响，与试验结果进行对比分析，得出如下结论：

(1)对RC柱拟静力试验，在OpenSees中选用不同钢筋与混凝土本构模型进行模拟时，计算结果差别较大，且采用不同钢筋与混凝土材料本构进行搭配建模时，对数值模拟的结果也有较大影响；对于钢筋本构，Steel02、ReinforcingSteel模拟效果比Steel01好，在确定选用Steel02还是ReinforcingSteel时，须视具体的混凝土本构模型来确定，Steel02与Concrete01、Concrete04或Concrete07搭配选用，ReinforcingSteel与Concrete01、Concrete02、Concrete07搭配选用时，分析效果相对更好；对于混凝土本构，其模型已比较成熟，其中Concrete01模拟效果最好。

(2)纤维截面划分形式对模拟结果有较大影响。平行于作用力的z方向截面划分m=1，垂直于作用力的y方向选n=10即可满足精度要求。

(3)基于位移插值的梁柱单元其划分数量对模拟结果有一定的影响。普通RC柱单元数量为5个就可达到足够的精度。

(4)单元积分点数对模拟结果影响相对较小，考虑到计算效率，积分点数为4精度已很好。

(5)本次数值模拟也存在不足：在模拟柱底钢筋粘结滑移时未深入研究零长度单元上截面材料本构参数的赋予，Concrete02本构与零长度单元并不能很好结合[25]，表现为模拟的滞回曲线普遍捏合不够好；试验中将试件加载到破坏，模拟时没考虑加载后期纵筋的屈服[19]。

本文主要进行的是等位移加载条件下的模拟分析，有关其它加载制度下的拟静力试验的数值模拟，如何选择最优的钢筋与混凝土本构搭配，将在后续工作中进行深入探讨。

[1] 周锡元. 中国建筑结构抗震研究和实践六十年[J]. 建筑结构, 2009, 39(9): 1-14.

[2] 陈 滔, 黄宗明. 钢筋混凝土框架非弹性地震反应分析模型研究进展[J]. 世界地震工程， 2002, 18(1): 91-97.

[3] 刘春燕. 基于OpenSees的单轴混凝土本构模型的实现[D]. 长沙: 中南大学, 2014.

[4] 陆新征, 叶列平, 潘 鹏, 等. 钢筋混凝土框架结构拟静力倒塌试验研究及数值模拟竞赛I: 框架试验[J]. 建筑结构, 2012, 42(11): 19-22.

[5] 陆新征, 叶列平, 潘 鹏, 等. 钢筋混凝土框架结构拟静力倒塌试验研究及数值模拟竞赛II: 关键构件试验[J]. 建筑结构, 2012, 42(11): 23-26.

[6] 中国建筑学会抗震防灾分会建筑结构抗倒塌专业委员会. 钢筋混凝土框架结构拟静力倒塌实验[EB/OL]. [2016-01-23]. http://www.collapse-prevention.net/download/NewsLetter03_2011-07-20.rar.

[7] 冷巧娟, 钱 江, 黄 频. 钢筋黏结滑移模型及OpenSees有限元模拟[J]. 华中科技大学学报(自然科学版), 2012, 40(11): 58-62.

[8] 陈 伟. 基于OpenSees平台开发的混凝土滞回本构模型在结构分析中的应用[D]. 重庆: 重庆大学, 2012.

[9] 刘立军, 贾明明, 于晓辉. 箍筋约束混凝土的本构关系研究[J]. 工业建筑, 2012, 42(s1): 188-191.

[10]B1akeley R W G, Park R. Prestressed concrete sections with cyclic flexures[J]. Journal of Structural Division, 1973, 99(8): 1717-1742.

[11]GB 50010-2001, 混凝土结构设计规范[S].

[12]Scott B D, Park R, Priestley M J N. Stress-strain behavior of concrete confined by overlapping hoops at low and high strain rates[J]. ACI Journal, 1982, 79 (1): 13-27.

[13]Yassin M H M. Nonlinear Analysis of Prestressed Concrete Sructures Under Monotonic and Cyclic Loads[D]. Berkeley: University of California, 1994.

[14]Popovics S. A numerical approach to the complete stress-strain curve of concrete[J]. Cement and Concrete Research, 1973, 3(5): 583-599.

[15]Laura Lowes. Concrete04 Material——Popovics Concrete Material[EB/OL]. [2016-01-23]. http://opensees.berkeley.edu/wiki/index.php/Concrete04_Material_--_Popovics_Concrete_Material.

[16]Mander J B, Priestley M J N, Park R. Theoretical stress-strain model for confined concrete[J]. Journal of Structural Engineering, 1988, 114(8): 1804-1826.

[17]Chang G A, Mander J B. Seismic Energy Based Fatigue Damage Ananlysis of Bridge Columns: Part 1-Evaluation of Seismic Capacity[R]. Buffalo: State University of New York, 1994.

[18]Sri Sritharan, Jonathan Waugh. Concrete07: Chang & Mander’s 1994 Concrete Model[EB/OL]. [2016-01-23]. http://opensees.berkeley.edu/wiki/index.php/Concrete07_-_Chang_%26_Mander’s_1994_Concrete_Model.

[19]张 行, 张谢东. 钢筋混凝土柱拟静力试验数值模拟分析[J]. 工程抗震与加固改造, 2013, 35(5): 30-35.

[20]陈 滔. 基于有限单元柔度法的钢筋混凝土框架三维非弹性地震反应分析[D]. 重庆: 重庆大学, 2003.

[21]聂利英, 李建中, 范立础. 弹塑性纤维梁柱单元及其单元参数分析[J]. 工程力学, 2004, 21(3): 15-20.

[22]杜 轲, 孙景江, 许卫晓. 纤维模型中单元、截面及纤维划分问题研究[J]. 地震工程与工程振动, 2012, 32(5): 39-46.

[23]宁超列, 段忠东. OpenSees中三种非线性梁柱单元的研究[J]. 低温建筑技术, 2009, 31(3): 49-52.

[24]周 亮. 基于OpenSees的RC框架结构非线性分析[D]. 湖南: 湖南大学, 2013.

[25]张鹏飞. 基于界面粘结滑移的约束混凝土柱本构关系的研究[D]. 唐山: 河北联合大学, 2013.

Numerical Analysis Model for Pseudo-static RC Columns Based on OpenSees

BUHai-feng1,HUSi-kang2,ZAHNGYao-ting1,TONGKang1,YEHong-wei1

(1.School of Civil Engineering and Mechanics，Huazhong University of Science and Technology，Wuhan 430074， China； 2.School of Civil Engineering，Wuhan University， Wuhan 430070， China)

The reinforced concrete column in equal displacement loading quasi-static test was analyzed by OpenSees. Considering the effects of different steel and concrete constitutive selection and match, fiber division, element division, integration points on numerical simulation, a reasonable and effective numerical model was made. The results indicate that:in OpenSees, the results vary greatly when selecting different steel and concrete constitutive models to simulate. Matching different steel and concrete constitutive models also have a greate effect on numerical simulation results; for steel constitutive, Steel02 and ReinforcingSteel simulation results are better than Steel01, and they matches different concrete constitutive; for concrete constitutive, Concrete01 simulates best; the form of fiber cross-sectional division has a great impact on the simulation results. When the fiber is dividedm=1 parallel to the direction of force,n=10 perpendicular to the direction of force,the result can meet the precision requirement; the number of elements has some influence on the simulation results, 5 elements can achieve the precision; integration points have little effect on the simulation results, when a element has 4 integration points, the calculation precision of the model is already high.

quasi-static tests of reinforced concrete column; OpenSees; constitutive model; fiber model; number of element integration

2016-03-07

2016-05-15

卜海峰(1993-)，男，湖北随州人，研究方向为结构工程(Email:U201315546@hust.edu.cn)

张耀庭(1965-)，男，湖北红安人，博士，教授，研究方向为钢筋混凝土结构抗震减震(Email:zyt1965@hust.edu.cn)

国家自然科学基金(51278218)；华中科技大学大学生创新创业训练计划项目(2015008)

TU375.3

A

2095-0985(2016)05-0021-07