基于参数变异性的车辙深度预估

张 勇，吴克宝，葛慧芝，罗 辉

(1.中交第二航务工程局有限公司第五工程分公司, 湖北 武汉 430012；2.武汉华中科大土木工程检测中心, 湖北 武汉 430074；3.河南省平顶山中亚路桥建设工程有限公司, 河南 平顶山 467000；4. 华中科技大学 土木工程与力学学院, 湖北 武汉 430074)



基于参数变异性的车辙深度预估

张 勇1，吴克宝2，葛慧芝3，罗 辉4

(1.中交第二航务工程局有限公司第五工程分公司, 湖北 武汉 430012；2.武汉华中科大土木工程检测中心, 湖北 武汉 430074；3.河南省平顶山中亚路桥建设工程有限公司, 河南 平顶山 467000；4. 华中科技大学 土木工程与力学学院, 湖北 武汉 430074)

合理的车辙预估是改善车辙设计的基础，对车辙进行合理预估能够在设计阶段就采取措施，降低车辙病害发生的几率与程度。本文在基于全厚度车辙试验的车辙预估模型的基础上，考虑影响路面车辙发展的温度、轴载、车速不是一个常数的事实，而通常车辙预估模型对应的参数只是取一个统计意义上的均值，没有考虑具体分布变异的影响，对建立的车辙预估模型进行了参数统计变异性分析，进一步建立了考虑参数统计变异性的车辙预估模型。得到如下结论：温度、速度统计变异性对车辙预估结果影响较大，随着统计变异性的增大，车辙预估值增大；轴重统计变异性对车辙预估结果影响较小；对车辙预估模型进行统计变异性修正后，可以提高预估精度。

车辙预估； 变异性； 全厚度车辙试验； 温度； 轴重； 车速

沥青因其优秀的路用性能广为应用，而车辙问题严重影响着沥青路面使用寿命与服务质量。实践表明，车辙破坏是造成路面结构破坏，降低路面服役性能的最严重的损坏模式之一，损害普遍存在且容易反复，构成交通安全隐患。

合理的车辙预估是改善车辙设计的基础，对车辙问题进行合理预估能够在设计阶段就采取措施，预防和降低车辙病害发生的几率与程度。通过建立的车辙预估模型，预估所设计路面的抗车辙能力，判断路面结构设计和材料设计是否达到规范要求或设计目标，以实现对设计的校核，可以改善设计的合理性。

吴瑞麟等围绕全厚度车辙试验进行了一系列的研究，进行了不同条件下的全厚度车辙试验，并取得了一些成果[1～3]。关宏信等研究了考虑沥青路面面层温度梯度的全厚度试验[4]。杨博等用有限元数值模拟方法论证了研究沥青路面组合结构车辙试验的可行性，并在此基础上进行了沥青路面高温抗车辙性能试验，分析了沥青混合料材料因素和组合结构因素对车辙性能的影响[5, 6]。罗辉等[7～9]基于全厚度车辙试验(可以反映沥青路面材料、路面组合结构、整体厚度的效应)，通过改变试验条件，获取了轴载作用次数、轴重、温度等对车辙的影响规律；在此基础上，利用有限元分析方法探明了速度对车辙的影响规律，最终，整合得到形式简单的车辙预估模型。

(1)

式中：R′(N)由车辙试验曲线直观可得；N4h为车辙试验4 h的碾压次数；R′(N4 h)为4 h时刻试验试块的永久变形量，即N=N4h时R′(N)的值，单位为mm；DS′为车辙试验曲线上4 h时刻的曲线切线的斜率，即N=N4h时R′(N) 的导函数的值；N是沥青路面结构及材料设计的基础参数，且式(1)中N>N4h；[R′(N4h)+(N-N4h)DS′]由车辙试验曲线得到，综合反映了室内车辙试验的结果，表征路面材料性能及路面结构设计的影响；T、L、V分别代表温度(℃)、轴载(MPa)、速度(km/h)，T0、L0、V0分别代表参考温度(℃)、参考轴载(MPa)、参考速度(km/h)；C1、C2、C3分别为待标定的温度、轴载、速度影响参数；A表示反映尺寸效应的系数。经标定后，得到式(2)。

(2)

但是，式(2)得到的车辙预估模型，输入参数中的温度、轴重、速度为常数，通常经统计而来，按一定的规则取均值，或转化后的均值。事实上，在沥青路面运营过程中，所经历的温度是不断变化的，行车荷载的轴重也是在一定范围内分布的，速度也一样。因此，采用统计均值作为式(2) 的输入，忽略其实际的分布规律，对预估结果是否有影响需要进一步的研究。

本文在基于全厚度车辙试验的车辙预估模型的基础上(式(2))，分析温度、轴重、速度的统计变异性对预估结果的影响规律，在此基础上，对式(2)作进一步的修正，以更真实地反映路面的实际运营状态，提高车辙预估模型的精度。

1 温度、轴重、速度的统计规律

考虑车辙多发于高温季节，且温度越高、轴载越重、速度越慢，车辙变形越严重，本章探索沥青路面建成后投入运用过程中温度、轴载、速度等的统计变异性对车辙预估的影响规律，出于简化考虑，将温度、轴载、速度的分布规律都按正态分布来考虑，并定义标准差与均值的比值为统计变异性。参数统计包括温度、轴载和速度等参数的概率分布和变异性，本节变异性分析按表1的统计规律来进行。

表1 参数概率分布特征

2 温度统计变异性分析

假设温度分布服从正态分布，均值为40℃，标准差变异性分别为0(相当于温度不变的情况)、5%、10%、15%、20%、25%、30%、35%的正态分布。取轴载作用100000次。为考察温度变异性对预估模型的影响，取轴重为100 kN、车速80 km/h保持不变。利用式(2)，分别计算不同工况下的车辙深度。

车辙计算方法：首先，计算不同温度下作用的分布概率(均值±3倍标准差范围内，保证概率99.7%)；然后，计算出不同温度下荷载作用次数；接着，利用式(2)分别计算不同温度下的车辙变形量；最后，汇总各温度下的车辙变形，即为该工况下的车辙深度计算值。具体如表2所示。

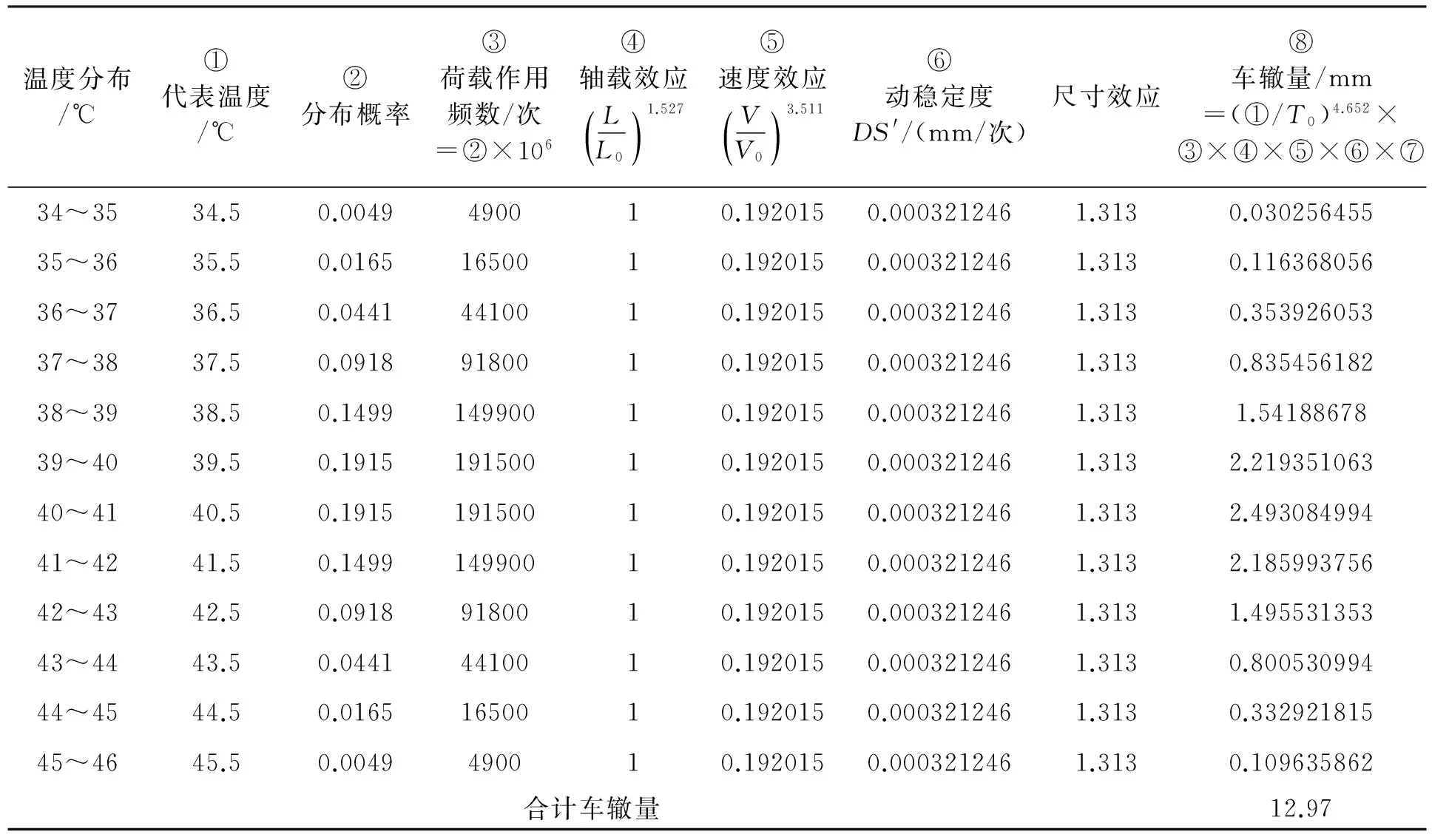
表2 温度统计变异系数为5%的车辙预估值计算

为简化分析，考虑车辙变形在稳定阶段发展，则式(2)可简化为：

(3)

根据试验结果[2]，取DS′=0.000321246，T0=60 ℃，L0=100 kN，V0=50 km/h温度统计变异系数为0时的车辙量计算值为：

为节省篇幅，温度变异系数为10%和35%的车辙计算表格未列出。

汇总温度变异系数为0～35%的车辙计算结果，可得到图1。

由图1分析可知，车辙变形量随着温度变异性的提高，车辙量呈增大趋势。用δ表示变异系数；RT变异表示考虑温度单独变异性影响得到的车辙变形量；R0表示变异性为0时的车辙变形量。绘制温度变异系数δT和RT变异/R0的关系曲线(图2)，拟合得到δT和RT变异/R0存在如式(4)的关系，相关系数R2=0.999。

图1 温度统计变异性对车辙预估值的影响

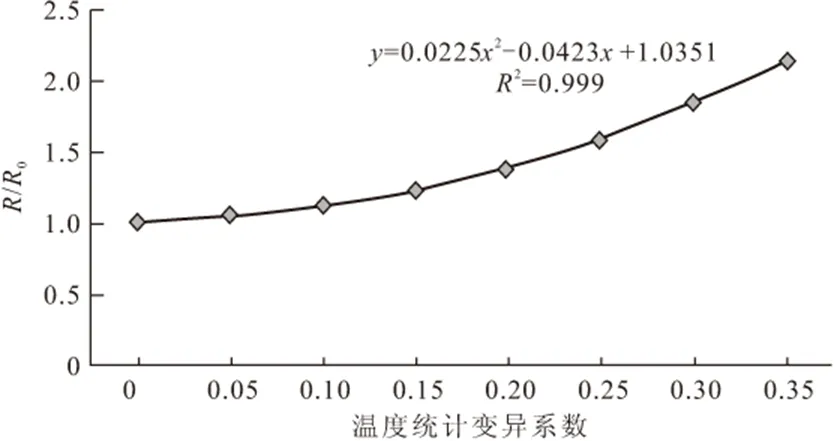
图2 温度统计变异系数和RT变异/R0 的关系

(4)

3 轴载统计变异性分析

假设轴载分布服从正态分布，均值为100 kN，标准差变异性分别为0 (即轴载不变的情况)、5%、10%、15%、20%、25%、30%、35%的正态分布。取轴载作用100000次。为考察轴载变异性对预估模型的影响，取温度为40 ℃、车速80 km/h保持不变。利用式(3)分别计算不同工况下的车辙深度，部分计算结果如表3所示。

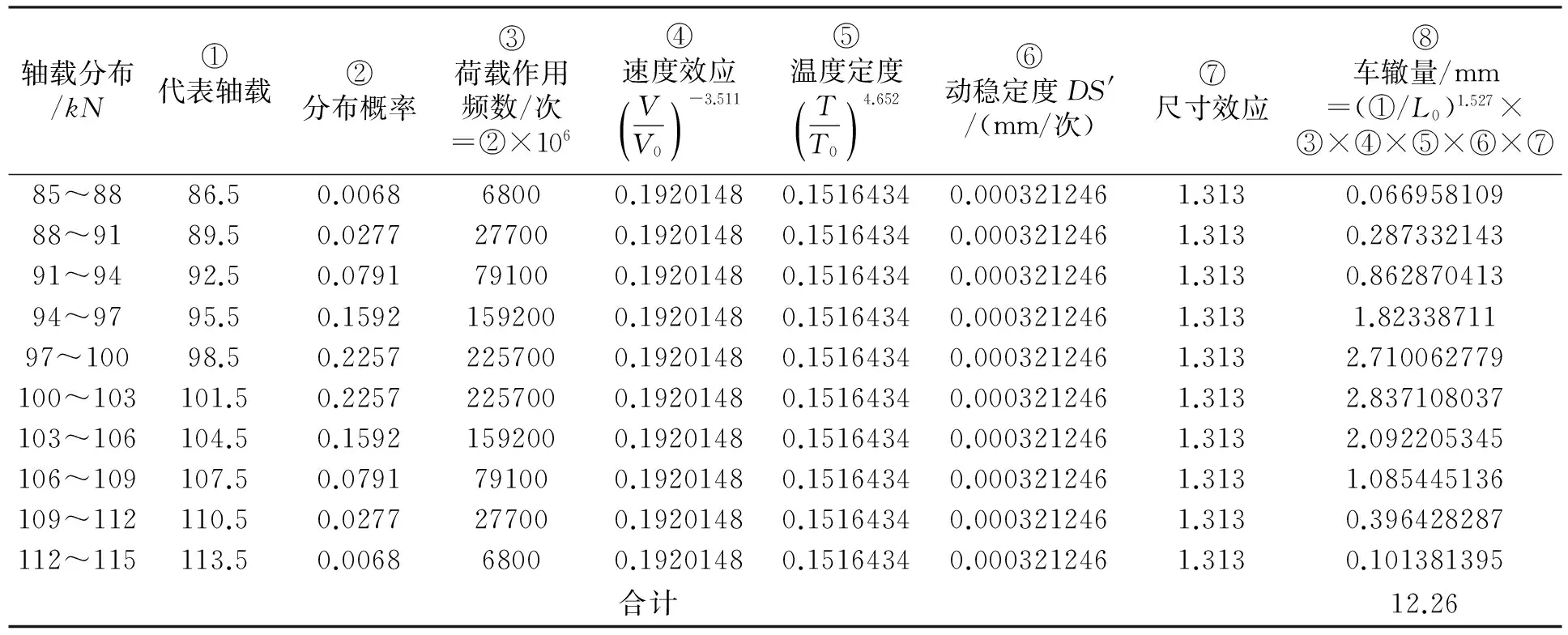
表3 轴载统计变异系数为5%的车辙预估值计算

为节约篇幅，轴载统计变异系数为10%～35%的车辙预估值计算表没有列出。

轴载统计变异系数与车辙量的关系如图3所示。

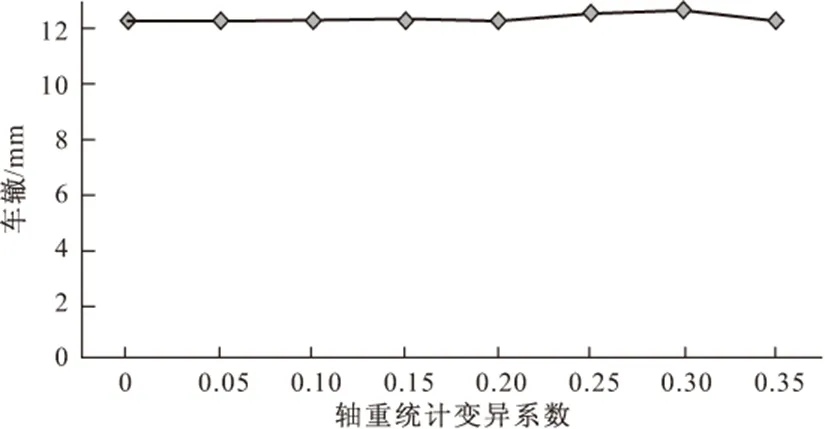
图3 轴载参数变异系数对车辙预估值的影响

由图3可知，车辙变形量受轴载值的变异性影响较小，基本保持不变。究其原因，是因为轴次的统计已经将所有轴载的作用次数按照标准轴载进行了转化，轴载越大，单次作用统计的荷载作用次数就越大，因此，轴载的偏差已经通过荷载作用次数得到了反映。由于车辙变形量基本不受轴载的统计变异性的影响，因此，可以不考虑对轴载进行车辙预估的修正。

4 速度统计变异性分析

假设速度分布服从正态分布，均值80 km/h，标准差变异性分别为0(相当于温度不变的情况)、5%、10%、15、20%、25%、30%、35%。取轴载作用100000次。为考察速度变异性对预估模型的影响，取轴载为100 kN、温度40 ℃保持不变。利用式(3)分别计算不同工况下的车辙深度，部分计算结构如表4所示。

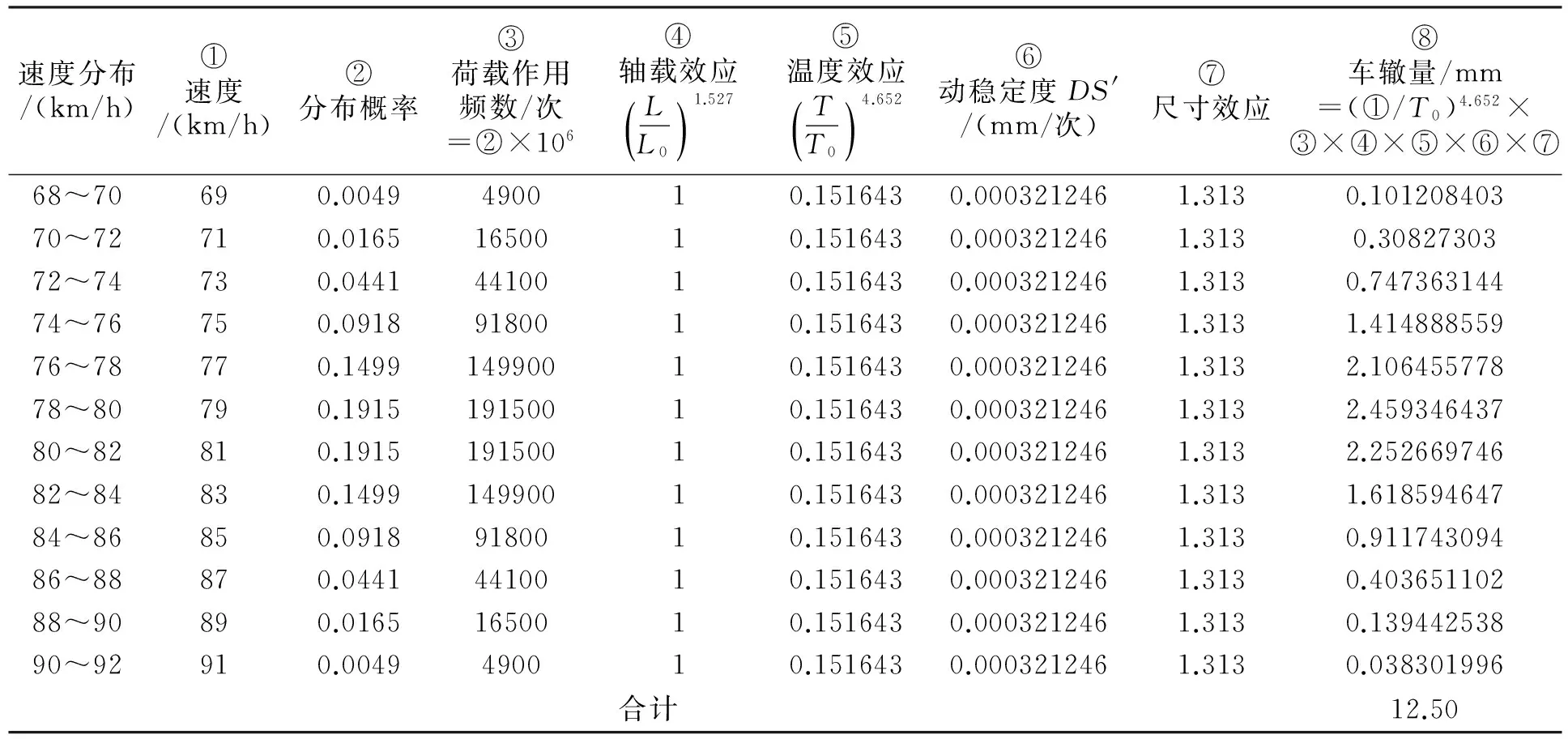
表4 速度统计变异系数为5%的车辙预估值计算

为节约篇幅，速度统计变异系数为10%～35%的车辙预估值计算表没有列出。

速度统计变异系数与车辙量的关系图如图4所示。

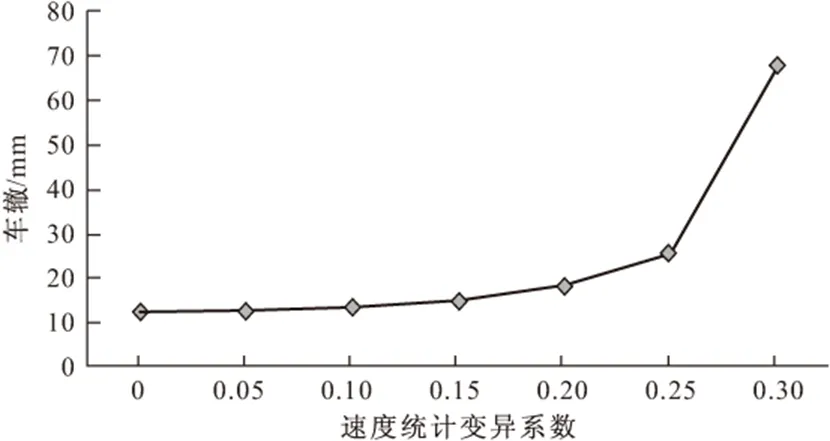
图4 速度参数变异系数对车辙预估值的影响

由图4可知，车辙变形量随着速度统计变异系数增大而增大。用δ表示变异系数，RV变异表示考虑轴载单独变异性影响得到的车辙变形量，R0表示变异性0时的车辙变形量，即由式(2)计算得到的车辙变形量，绘制速度统计变异系数δV和RV变异/R0的关系曲线(图5)，拟合得到δV和RV变异/R0存在如式(5)关系，R2=0.8175。

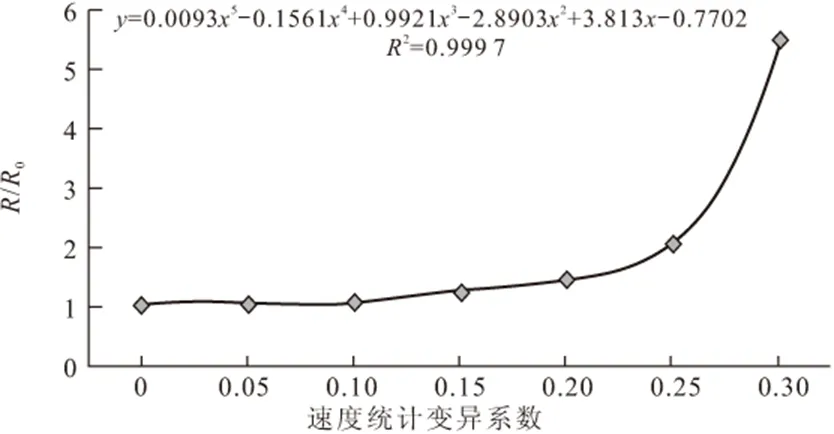
图5 速度统计变异系数和RV变异/R0的关系

(5)

5 基于统计变异性分析的车辙预估模型修正

基于前面的参数统计变异性分析，在式(2)基础上，进一步对车辙预估模型进行修正。基于简化考虑，假设温度、轴载、速度等三个因素对车辙的发展互不影响，即彼此之间是独立的，对(2)进行温度影响、速度影响修正，得到考虑了温度和速度参数变异性影响的车辙预估模型，如式(6)。

(6)

式中：温度和速度变异性影响系数αT、αV的计算如式(7)、式(8)。

(7)

αV=0.0093δV5-0.1561δV4+0.9921δV3-2.8903δV2+3.813δV-0.7702

(8)

式中：δT、δV分别为温度统计变异系数和速度统计变异系数。

为了验证式(6)相对于式(2)的优越性，选取合适工况进行车辙预估结果比较分析，具体地，统计平均温度40 ℃、轴载100 kN、速度80 km/h，作用2000000轴次，选取如下4种组合工况进行比较分析：(1)前1000000次轴载作用，温度变异系数为10%，速度变异系数为0，后1000000次轴载作用，温度变异系数为0，速度变异系数为10%；(2)前1000000次轴载作用，温度变异系数为20%，速度变异系数为0，后1000000次轴载作用，温度变异系数为0，速度变异系数为20%；(3)前1000000次轴载作用，温度变异系数为20%，速度变异系数为0，后1000000次轴载作用，温度变异系数为0，速度变异系数为10%；(4)前1000000次轴载作用，温度变异系数为10%，速度变异系数为0，后1000000次轴载作用，温度变异系数为0，速度变异系数为20%。

对于工况1，根据统计理论，可知此时δT=0.0707 ，δV=0.0707；工况2时，δT=0.1414，δV=0.1414；工况3时，δT=0.1414，δV=0.0707；工况4时，δT=0.0707，δV=0.1414 。代入式(6)，即可得到修正后的车辙预估值。不同工况下，由式(2)和式(6)计算得到车辙预估值，具体如表5所示。由表5可见，经过参数统计变异性的修正，预估模型的精度得到了较大的提高，证明了模型修正的有效性。而且从表中数据可以看出，如果不考虑温度、速度等参数的统计变异性，预估得到的结果将严重偏小，这对于设计来说是不安全的，因此，在进行车辙预估建模时有必要考虑温度、速度等参数的统计变异性。

表5 不同工况车辙预估值

6 结 论

本文主要对温度、速度、轴重的参数统计变异性对车辙预估结果的影响进行了分析。并在此基础上，对车辙预估模型进行了统计参数变异性的修正。得到如下结论：

(1) 温度、速度统计变异性对车辙预估结果影响较大，随着统计变异性的增大，车辙预估值增大。

(2)轴重统计变异性对车辙预估结果影响较小，车辙预估值基本保持不变，原因是轴次的统计已经将所有轴重的作用次数按照标准轴重进行了转化。

(3) 数值算例分析证明，对车辙预估模型进行统计变异性修正后，可以提高预估精度。

[1] 李 娜, 朱文琪, 李向东, 等. 全厚度与标准厚度车辙试验的对比分析[J]. 武汉理工大学学报, 2003, 25(12): 66-68.

[2] 李 娜. 全厚度车辙试验的研究[D]. 武汉: 华中科技大学, 2006.

[3] 石立万, 王端宜, 吴瑞麟. 温度荷载联合作用下沥青路面全厚度车辙研究[J]. 华中科技大学学报(自然科学版), 2013, 41(11): 37-40.

[4] 关宏信, 张起森, 罗增杰. 考虑温度梯度沥青路面面层全厚式车辙试验[J]. 土木工程学报, 2011, 44(6): 143-147.

[5] 杨 博, 张争奇. 沥青路面组合结构车辙试验研究[J]. 武汉理工大学学报, 2012, 34(7): 46-50.

[6] 杨 博. 基于有限元方法的沥青路面车辙影响因素分析及其应用研究[D]. 西安: 长安大学, 2010.

[7] 陈斯宁, 罗 辉, 周美茜, 等. 一种评估沥青路面抗车辙能力的方法[J]. 南阳理工学院学报, 2015, 7(4): 79-82.

[8] 宋俊伟, 方紫微, 陈斯宁, 等. 基于全厚式车辙试验的沥青路面车辙预估[J]. 交通科技, 2016, (1): 68-71.

[9] 冉隆举, 陈斯宁, 罗 辉, 等. 全厚度车辙试验与足尺加速加载试验相关性研究[J]. 公路, 2015, (12): 51-55.

The Rutting Predication of Asphalt Pavement Based on Variability Analysis

ZHANGYong1,WUKe-bao2,GEHui-zhi3,LUOHui4

(1.No 5 Branch of CCCC second Harbor Engineering Co Ltd, Wuhan 430012, China; 2.Wuhan Huazhong Keda Civil Engineering Testing Center, Wuhan 430074, China; 3.Pingdingshan Zhongya Road and Bridge Construction Engineering Co Ltd, Henan Province, Pingdingshan 467000, China; 4.School of Civil Engineering and Mechanics, Huazhong University of Science and Technology, Wuhan 430074, China)

A reasonable rutting prediction is fundamental to rutting resistance design, which aims at establishing a model to predict rutting resistance of the pavement to judge whether the pavement structure design and material design meet the requirements of the specification or design goal or not, and finally causing less rutting failure. Considering parameters of rutting prediction model such as temperautre, wheel load and vehicle velocity were normally set as statistical constants rather than variables with specific distribution variation, the statistical variability of parameters is analyzed to investigate the influence to rutting predication, and modified the rutting predication model to improve its accuracy. These conclusions are obtained: the rutting predication is obviously influenced by the statistical variabilities of temperature and vehicle velocity, greater statistical variabilities causing deeper rut; the statistical variability of wheel load have little influence on the rutting prediaction; and after the modificaiton of the statistical variability, the accuracy of the rutting predication is enhanced.

rutting predication; statistical variability; total-thickness rutting test; temperature; wheel load; vehicle velocity

2016-05-13

2016-07-11

张 勇(1978- )，男，湖北武汉人，工程师，研究方向为高速公路施工管理(Email:37927957@qq.com)

罗 辉(1979- )，男，湖北武汉人，副教授，博士，研究方向为结构健康监测和沥青路面结构行为 (Email: autumn_luoh@163.com)

国家自然科学基金(51578261)；湖北省科技支撑计划项目(2015BAA112)；中央高校基本科研业服务费专项资金(2015MS071)

U416.217

A

2095-0985(2016)05-0033-05