《九章算术》方程章“麻麦”问刘徽注中“算”字新释及方程“旧术”新校

魏雪刚 郭世荣

(内蒙古师范大学科学技术史研究院,呼和浩特 010022)



《九章算术》方程章“麻麦”问刘徽注中“算”字新释及方程“旧术”新校

魏雪刚 郭世荣

(内蒙古师范大学科学技术史研究院,呼和浩特 010022)

在分析前人对《九章算术》方程章“麻麦”问之刘徽注中的方程“旧术”和“新术”的研究基础上,对其中“凡用七十七算”和“一百二十四算”之“算”做了新的解释,认为“算”可做算筹解。此外,讨论了校正“旧术”需要注意的几个问题,并给出了与前人不同的新校正。

算 《九章筭术》方程章 方程旧术

刘徽在《九章算术》方程章第十八问“麻麦术”的注文中,有关于方程“旧术”和“新术”的讨论。数学史家对于新、旧二术的理解,虽然都能在算理上说得通,但是在对刘徽注文的具体疏通校勘上却有不同的解读。其中,各家对方程“新术”的校勘结果没有本质差别,且演算程序一致,而对“旧术”的术文校正则颇多分歧。清代戴震整理《九章算术》时就认为旧术文字“讹舛不可通”([1],187页)。从他开始,不断有学者对这段文字进行校正。这里,一个关键点是,刘徽在“旧术”结尾时总结说“如此凡用七十七算”,在“新术”后又说“如此凡一百二十四算”。然而,迄今为止,虽然各家已有的校改与解释均能够从数理和演算上自成体系,但都不能很好地解释刘徽“凡用算若干”类用语的意思。因而刘徽所言“算”指什么？数学史学者一直没有公认的意见,依然见仁见智。

既然大家对“新术”理解相同,没有疑义,那么我们就可以尝试从新术中寻求刘徽在什么意义上使用“算”字,然后再考察这个意义在旧术中能不能说得通。如果可以解释得通,则说明对“算”的理解有其合理性。本文在假设“七十七算”和“一百二十四算”无误的前提下,首先解释“新术”中“一百二十四算”之“算”的含义,然后对“旧术”进行再校,分析它的“凡用算”情况,再结合“新旧”两术给出对“算”的一种解释。仅提供一家之言,就正于方家。

1 “算”的释义

史家对“算”有三种具体解释*白尚恕《九章算术注释》(北京：科学出版社,1983,第293页)给出了“旧术”细草,认为“凡用七十七算”为“共计77次运算”,但没有给出如何算作一次运算。我们分析了几种可能性,均未得到相合的解释,故暂不论此说。。第一,李继闵《〈九章算术〉校证》统计“新术”用124算时认为“每算出行、列中某位上一个新数据,称为一‘算’”([2],454页)。第二,李继闵《〈九章算术〉导读与译注》按照每算出行、列中某位上一个数据,称为一“算”来统计“旧术”所用的77算([3],674～676页)。第三,郭书春《〈九章算术〉译注》*1998年辽宁教育出版社出版的郭书春《九章算术》译注本与《〈九章算术〉译注》本对“算”解释一样,今取后者为例。认为“一算即一次运算”([4],362～364页)。

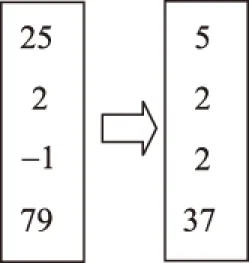
图1 算例示图

下面我们对这三种解释逐一进行分析。首先看第一种理解,它认为算出行列一个新数据为一算,也就是说,如果算得数据与旧数据相同则不能当做一算。举例来说,如图1,左侧数据经过运算得到右侧数据,其中改变了三个数据,所以这次运算当作3算。李继闵统计“新术”用124算即采用这种说法。这里有两点需要指出,首先,化简相约时得到的新数据应该计算在内,李继闵没有考虑这部分；其次,“新术”可以分为三部分,第一部分计算出“相与之率”,第二部分用“今有术”求解,第三部分用“列衰术”求解。刘徽说“如此凡用一百二十四算”,并没有明确说明计算到哪一步为止,所以三种可能都要考虑,即计算到“相与之率”为止,到“今有术”为止,到“列衰术”为止。我们对“新术”核算的结果是共用了119+20+8算,也就是说,计算到“相与之率”为止用了119算,到“今有术”为止用了139算,到“列衰术”为止用了147算,无论如何都满足不了124算。另外,按照这种理解,统计李继闵校正的“旧术”所用的“算”数,结果是68算,不是77算。

第二种理解认为无论重复与否,只要某个数据参加运算即为一算。上例中虽然有一个数据没有变动,也应该当作一算,所以上例共4算。按此理解,李继闵校正的“旧术”所用的“算”数为77算。但是当用这种理解考察“新术”时,得到的“算”数却是142+20+10算,结果是142算或162算或172算,皆与124算不符。

第三种理解认为运算一次就是一“算”。按此,上例当为1算。郭书春认为依照这种理解，他校正的“旧术”满足77算。按照他的统计规则*郭书春认为类似“A行去B行头位”这样的论述,假设A行头位数为a,B行头位数为b,则它的运算步骤是：布置B行,以a遍乘B行,再b次减A行；统计“算”的规则是：“布置”为1算，“遍乘”为1算，b次减为b算,共1+1+b算。如“以第二行去第四行头位”,第四行头位为2,则本次“算”为1+1+2,即共4算。,“以右行去第二行头位”一句,因第二行头位为20,应该是22算,而不是21算。所以其“旧术”应该是78算,而不是77算。再者,利用这种对“算”的解释,统计“新术”用算数当为250+11+6算,结果或250算或261算或267算,皆与124算不符。

综上,这三种对“算”的解释,只有第二种解释符合了李继闵对“旧术”的校正,其余则有出入。另外,它们都不能与“新术”用124算的论述相吻合。也就是说,以上三种对“算”的解释有进一步讨论的空间。

本文对“算”提出一种新的解释,即每用一根算筹为一“算”。也就是说,“凡用算”指整个运算过程中用筹最多的一次计算所用算筹数。这里有两点需要说明,第一,负数的“邪置”我们认为是斜放的意思,笔录中用斜杠表示负数,大概由此而来；第二,因为中算有“副置”的习惯,我们认为“旧术”中每步的具体演草过程当在主筹算板外另外计算,这部分演算不在考虑范围之内。分析“新术”细草可知,整个过程只有“次以左行减第三行下位。次以第三行去左行下位,讫,废去第三行”([1],187页)中的“次以左行减第三行下位”及“次以第三行去左行下位”两步骤用筹最多,皆为124根算筹,分别见图2*其中右、二、三、四、左表示第几行,( )内的阿拉伯数字表示本次用筹数,为了方便筹算都换成阿拉伯数字。以下皆仿此。、图3。为节省篇幅,不再逐一列出细草。另外,刘徽在论述新旧术之前有段类似引言的话,其中谈到“记其施用之例,著策之数,每举一隅焉。”([1],186页)“策”就是算筹。由此可以看出,统计用算筹的数量是他的目的之一,所以“新术”中“凡用一百二十四算”是他统计的“著策之数”。

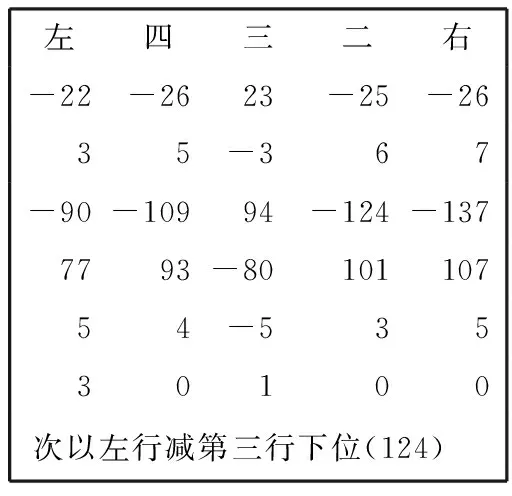
左四三二右-22-2623-25-2635-367-90-10994-124-1377793-8010110754-53530100次以左行减第三行下位(124)

图2 “次以左行减第三行下位”算图

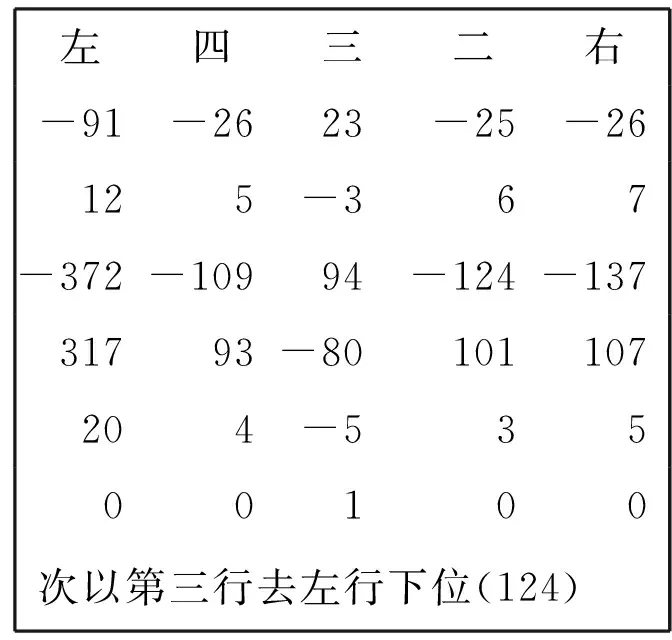
左四三二右-91-2623-25-26125-367-372-10994-124-13731793-80101107204-53500100次以第三行去左行下位(124)

图3 “次以第三行去左行下位”算图

2 刘徽注方程“旧术”新校

2.1 各家对“旧术”的校勘

根据郭书春的研究,现存方程章的版本有两个系统[5]。前人对方程章“旧术”的校勘多以这两个系统中的某一个或某几个版本为底本。通过对校乾隆御览本[1]、宜稼堂丛书《详解九章算法》[6]、《四库全书》本[7]、微波榭本[8],并且参考宋景昌《详解九章算法札记》[9],发现这些版本只有一字之差,为了方便起见,暂称它们为杨辉本。这段文字衍脱严重,不易通读,但它却是各家校证的基础,现录如下*因研究者对这段文字的句读有所差别,故此处暂不加标点。：

以旧术为之凡应置五行今欲要约先置第三行以减第四行及减第三行次置第二行以第二行减第三行去其头位次置右行去其头位次以第四行减左行头位次以左行去第四行及第二行头位次以第五行减第二行头位余可半次以第二行去第四行头位余约之为法实如法而一得空即有黍价以法治*宜稼堂丛书《详解九章算法》等本此处为“减”,郭书春在《汇校〈九章算术〉》(增补版,上)校勘记中指出宋校本、补刊本、钱校本依孔刻本采用“治”字,其增补本从此说([10],400页)。李继闵也从此说。今从之。第二行得荅价左行得麦价第三行麻价右行得菽价如此凡用七十七算

2.1.1 戴敦元的校勘结果

李潢在《〈九章算术〉细草图说》中给出了戴敦元的一个校正。此书以“微波榭本为底本细草图说”([5],91页),推测戴敦元可能是以微波榭本为底本做的校勘。这种校正改10字,添26字,移29字,共65字([10],414页)。以后各家,如李锐[11]、李潢[12]、钱宝琮[13]、白尚恕[14,15]、沈康身[16]等,对“旧术”的校正虽然有时会用到不同的底本,但结果皆与此一致,故不再考虑他们的校正情况,仅录出戴敦元校正本为例做一说明。戴敦元校改结果如下：

先置第四行,以减第三行。反减第四行,去其头位。次置第二行,以第三行减第二行,去其头位。次置右行及左行,去其头位。次以第二行减右行头位。次以右行去左行及第二行头位。又去第四行头位,余,可半。次以第四行减左行头位。次以左行去第四行及第二行头位。次以第二行去第四行头位,余,约之为法。实如法而一,得六,即黍价。以法减第二行得荅价,左行得菽价,右行得麦价,第三行麻价。([12],1170～1171页)

2.1.2 李继闵的校勘结果

通过对校可知,李继闵《〈九章算术〉校证》校证该部分所用的底本与杨辉本相同。他的校正改2字,添8字,删24字,移9字,共43字([2],101页)。李继闵校勘结果如下：

以旧术为之,凡应置五行。今欲要约,先置第三行。以第四行反减第三行。以第三行去其头位。次以第二行减右行。次置右行去其头位；余可半。次以第四行减左行。次以左行去第四行及第二行头位。次以第二行去第四行头位。余,约之为法、实。如法而一得六,即黍价。以法治第二行得荅价,左行得菽价,右行得麦价,第三行麻价。如此凡用七十七算。([2],101页)

2.1.3 郭书春的校勘结果

1990年郭书春在《汇校〈九章算术〉》一书中对“旧术”进行了校正,2004年他在《汇校〈九章算术〉(增补版)》(以下简称“增补本”)中做了修订,得到新的校正结果。经过比较可知,其后他对“旧术”的校正都依此说[4,17- 19]。所以,这里只给出他2004年的这种校正。对校知道,他对该部分的校正所用的底本与杨辉本一致。他的校正改11字,添30字,删4字,移8字,共53字([10],401页)。其结果如下：

以旧术为之,凡应置五行。今欲要约。先置第三行,减以第四行,又减第五行；次置第二行,以第二行减第一行,又减第四行,去其头位；余,可半；次置右行及第二行,去其头位；次以右行去第四行头位；次以左行去第二行头位；次以第五行去第一行头位,次以第二行去第四行头位；余,可半；以右行去第二行头位,以第二行去第四行头位。余,约之为法、实,实如法而一,得六,即有黍价。以法治第二行,得荅价,右行得菽价,左行得麦价,第三行麻价。如此凡用七十七算。([10],368页)

2.2 “旧术”再校

对“旧术”的校正需要考虑如下几个问题：

(1)应该合理解释“置”字。原文“以旧术为之,凡应置五行,今欲要约,先置第三行”中的两个“置”意义相同,即放置或摆放。李继闵将后一“置”训为“搁开或废置”([2],99页),值得进一步讨论。刘徽为了“要约”并不是像传统的方程术那样,把五行全部摆放在算板上,而是逐一放置,且每次放置时都会说明,所以在没有说明的情况下不应该自行放置。但是,戴敦元本自行放置了第三行,郭书春自行放置了第四行。

(2)要注意左右行问题。通过方程章文本分析可知,没有把左行说成是第五行,把右行说成第一行的情况,在校正“旧术”时应该遵从这个原则。另外,左右两字容易混淆,而左、右与第几(如第一、第二等)是不易混淆的,故校正时应该尽量不要把左、右行与第几行互改。戴敦元本出现了第五行,并且有三处左、右行与第几行互改的情况。增补本出现了第五行及第一行,并且有一处把右行与第四行互改的情况。

(3)李继闵认为“旧术”消元的先后顺序共有两种可能,“三、右、左、二、四”和“三、左、右、二、四”[2]。究竟应该是哪一种呢？因为我们在校证原文之前暂无法确定“旧术”中关于消元的次序,也就是说暂不把消元的顺序作为判断校正是否合理的依据。

(4)校正应该较少地改动原文,这不仅涉及改动字数多少问题,而且还要考虑校正与原文的符合程度。

基于以上考虑,我们以杨辉本为底本给出新校如下：

以旧术为之,凡应置五行,今欲要约,先置第三行及第四行,以减第三行。次置第二行,以第三行减第二行,去其头位。次置右行,去其头位。次以第二行减右行。次去第四行头位。次以右行去第四行及第二行头位,余可半。次以第四行去第二行头位。次置左行,去其头位。次去左行及第四行头位。次以第二行去第四行头位,余，约之为法。实如法而一,得六,即有黍价。以法治第二行得荅价,左行得菽价,右行得麦价，第三行麻价。如此凡用七十七算。

此校改6字,添25字,删3字,移12字,共46字。

李继闵曾把底本分为8个片段[2],讨论校正后与底本相符程度。结果是戴敦元本有2个片段与底本一致,3个片段与底本较为接近,改写了3个片段,增添了2个片段。按照他的规则,我们分析李继闵“校证本”知,它有2个片段与底本一致,4个片段与底本较为接近,改写了2个片段,增添了1个片段。增补本有1个片段与底本一致,4个片段与底本较为接近,改写了3个片段,增添了2个片段。我们的校正有2个片段与底本一致,3个片段与底本较为接近,改写了3个片段,增添了3个片段。综合地看,我们的校正在与底本相符程度上,较之各家并不逊色。另外,这个校正没有自行放置某行的情况,而且没有出现第一行,第五行,以及左右行与第几行互改的现象。下面我们给出新校演算图(图4),并统计其所用算筹数。

图4 新校方程旧术演算图

其中用筹最多一步用了77根算筹,符合“凡用七十七算”之说。

综上可知,把“算”作算筹解,符合了“凡用一百二十四算”和“凡用七十七算”之说。此外,考察刘徽在方程章中有关“算”的其他用法,如“其拙于精理徒按本术者,或用算而布毡,方好烦而喜误,曾不知其非,反欲以多为贵。”“虽布算不多,然足以算多。”[1]等句,也是把算解释为算筹的。现存清代以前的《九章算术》版本,均用“筭”字。《说文解字》说“筭：长六寸。计历数者。从竹从弄。言常弄乃不误也。”[20]此处“筭”即算筹。段玉裁在《说文解字注》称：“‘筭’为‘算’之器,‘算’为‘筭’之用,二字音同而义别。”[21]此处“筭”也作算筹解。概而论之,把方程章“麻麦”问刘徽注中的“算”字当作算筹解,有一定的合理之处。

致 谢 本文曾在上海交通大学夏至会上报告过,得到与会师友诸多宝贵意见,特此致谢。感谢赵佳佳同学帮助进行部分数据计算。感谢审稿人的建设性意见。

1 九章算术[M]//郭书春.中国科学技术典籍通汇·数学卷.第1分册.郑州：河南教育出版社,1993．

2 李继闵.《九章算术》校证[M].太原：山西科学技术出版社,1993．

3 李继闵.《九章算术》导读与译注[M].西安：陕西科学技术出版社,1998．

4 郭书春.《九章算术》译注[M].上海：上海古籍出版社,2009．

5 郭书春.中国科学技术史·数学卷[M].北京：科学出版社,2010．

6 杨辉.详解九章算法[M].宜稼堂丛书.1842(道光壬寅)．

7 九章算术[M]//钦定四库全书·子部.文渊阁本．

8 九章算术[M]//靖玉树.中国历代算学集成.上.济南：山东人民出版社,1994.128～137．

9 宋景昌.详解九章算法札记[M]. 1842(道光壬寅)．

10 郭书春. 汇校《九章算术》·增补版[M].上.沈阳：辽宁教育出版社,台北：台湾九章出版社,2004．

11 李锐.方程新术草[M].《李氏遗书》十一种本．

12 李潢.《九章算术》细草图说[M]//郭书春.中国科学技术典籍通汇·数学卷.第4分册.郑州：河南教育出版社,1993．

13 钱宝琮.校点算经十书[M]//李俨钱宝琮科学史全集.第4卷.沈阳：辽宁教育出版社,1998.174～188．

14 白尚恕.《九章算术》今译.济南：山东教育出版社,1990.356～417．

15 白尚恕.《九章算术》注释[M].北京：科学出版社,1983.257～305．

16 沈康身.《九章算术》导读[M].武汉：湖北教育出版社,1997.535～618．

17 郭书春,刘钝.算经十书[M].沈阳：辽宁教育出版社,1998.84～94．

18 郭书春.九章算术[M]//赵敏俐.国学备览.北京：首都师范大学出版社,2007.259～268．

19 郭书春.《九章算术》新校[M].合肥：中国科学技术大学出版社,2014.327～380．

20 许慎.说文解字[M].北京：中华书局,1963.99．

21 段玉裁.说文解字注[M].上海：上海古籍出版社,1981.372．

22 汪莱.校正九章算术及戴氏订讹[M]//衡斋遗书.卷5.衡斋算学遗书合刻,闻梅旧墪藏板．

23 李继闵.《九章算术》方程章校证一例[J].自然科学史研究,1993,12(3):220～224．

24 郭书春. 汇校《九章算术》[M].沈阳：辽宁教育出版社,1990.385～417．

25 郭书春.《九章算术》方程章刘徽注新探[J].自然科学史研究,1985,4(1):1～5．

26 郭书春.《九章算术》译注[M].沈阳：辽宁教育出版社,1998.400～443．

A New Explanation of the Meaning of “Suan” and A New Collation of Liu Hui’s Text of the “Old Equation Method” in theNineChaptersonMathematicalArts

WEI Xuegang GUO Shirong

(InstituteforHistoryofScienceandTechnology,InnerMongoliaNormalUniversity,Hohhot010022,China)

Based on a survey of historical studies of Liu Hui’s commentary to the so-calledoldmethodandnewmethodattached to the 18thproblem of the equation chapter in theNinechaptersonMathematicalArts, a new explanation of the meaning of the conceptsuanis proposed in the present paper. The authors argue thatsuanin this context should be understood as the number of counting rods which are used in computation. In addition, some principles for the collation of theoldmethodare proposed, and based on those principles the text of theoldmethodis re-collated.

NineChaptersonMathematicalArts, equation,suan

2015- 10- 13；

2016- 03- 22

魏雪刚,1990年生,安徽界首人,硕士研究生,研究方向为数学史。

郭世荣,1959年生,教授,主要从事数学史和科技史研究。

N092∶O112

A

1000- 0224(2016)01- 0010- 08