中国古算书中运动学问题的数学解法与近代物理解法的比较

胡化凯 张阳阳

(中国科学技术大学科技史与科技考古系,合肥 230026)



中国古算书中运动学问题的数学解法与近代物理解法的比较

胡化凯 张阳阳

(中国科学技术大学科技史与科技考古系,合肥 230026)

从秦代至清中期,中国至少有24部算书共包含有上百道运动学算题。这些算题涵盖了匀速运动、匀变速运动和变加速运动三类内容。古人运用各种数学方法求解这些算题,无论是解题思路、思维方式,还是知识体系都与近现代运动学有明显的不同。文章将这些算题的传统数学解法与近现代物理解法进行了系统的分析比较,结果发现：对于匀速运动问题,数学解法与物理解法基本上是一致的；对于一些比较复杂的匀变速运动和变加速运动问题,数学解法与物理解法则有本质的不同。由此反映了古人独特的物理认知方式和解决问题的方法。由于中国古人对运动现象的认知方式是数学性的,而非物理性的,因而未能提出一般性物理概念,提炼出一般性物理问题,长期停留在一个认识水平上,无法发展成一般的运动学理论。

中国古算书 运动学问题 数学解法 物理解法 比较

中国古代有大量的数学著作,其中不少著作含有运动学算题,并给出了求解方法及答案。1997年,戴念祖先生基于对《九章算术》中运动学算题的分析指出：“以算题形式总结运动学知识,是中国物理学史的特点之一。”[1]次年,沈康身、李迪先生也称：《九章算术》对于匀加速、匀减速等运动的论述,“彪炳历史,成果不减西方,在时间上胜似西方”[2]。之后,周靖[3- 5]、李伯川[6]、陈育成[7]等都发表文章,对《九章算术》中的运动学内容进行了讨论。这些学者的讨论主要是基于《九章算术》的相关内容。笔者在编纂《中华大典·物理学分典》过程中,系统搜集了中国古算书中的运动学内容,结果发现,从秦代至清中期,至少有24部算书包含有运动学算题。这些算题涵盖了匀速运动、匀变速运动和变加速运动三类内容。古人把物理运动问题看作数学问题,采用传统的数学方法求解,无论是解题思路、思维方式,还是知识体系都与近现代运动学有明显的不同。由此反映了中国古人独特的物理认知方式和解决问题的方法。以前,科学史家们虽然认识到这些算题的物理涵义,但并未从物理学的角度分析古人解题的合理性及局限性,因而未能全面揭示其物理本质。明确古代运动学问题的数学解法与近代物理解法有何区别,是正确认识与合理评价古人这些工作的关键。将古人的数学解法与今日的物理解法进行系统的分析比较,即可看出数学解法的特点、性质、优势与不足,有助于正确理解古人对运动现象的独特认知方式及其局限性。

表1列出了这24部算书所属的时代、编作者、所含运动学算题的数量及类型。24部算书共有175个运动学算题,除去重复者,还有128题。根据题目内容,128个算题可分为三大类,其中112个属于匀速运动算题,9个属于匀变速运动(即匀加速、匀减速运动)算题,7个属于变加速运动算题。下面分类对这些算题的数学解法与物理解法进行分析比较,以期得出新的认识。由于算题较多,我们从10本算书中选择22个具有代表性的算题作案例,分类加以讨论。

表1 中国古算书中的运动学算题分类

①睡虎地汉简《算术》尚未有整理材料发表,目前仅能从《湖北云梦睡虎地M77发掘报告》(《江汉考古》,2008年第4期,第31～37页)所附“算术简”彩图中见到十支简的照片,其中即含有一道匀速运动问题。邹大海据照片首次给出了这道算题的释文。参见邹大海《从出土竹简看中国早期委输算题及其社会背景》(《湖南大学学报(社会科学版)》,2010年第4期,第5～10页)。

②《透簾细草》的作者及成书年代均不详,亦不见序跋。本文参考了邹大海《<透簾细草>提要》(《中国科学技术典籍通汇·数学卷(一)》,郑州:河南教育出版社,1993年,第1281页)一文中的观点,将此书置于朱世杰《算学启蒙》之后。

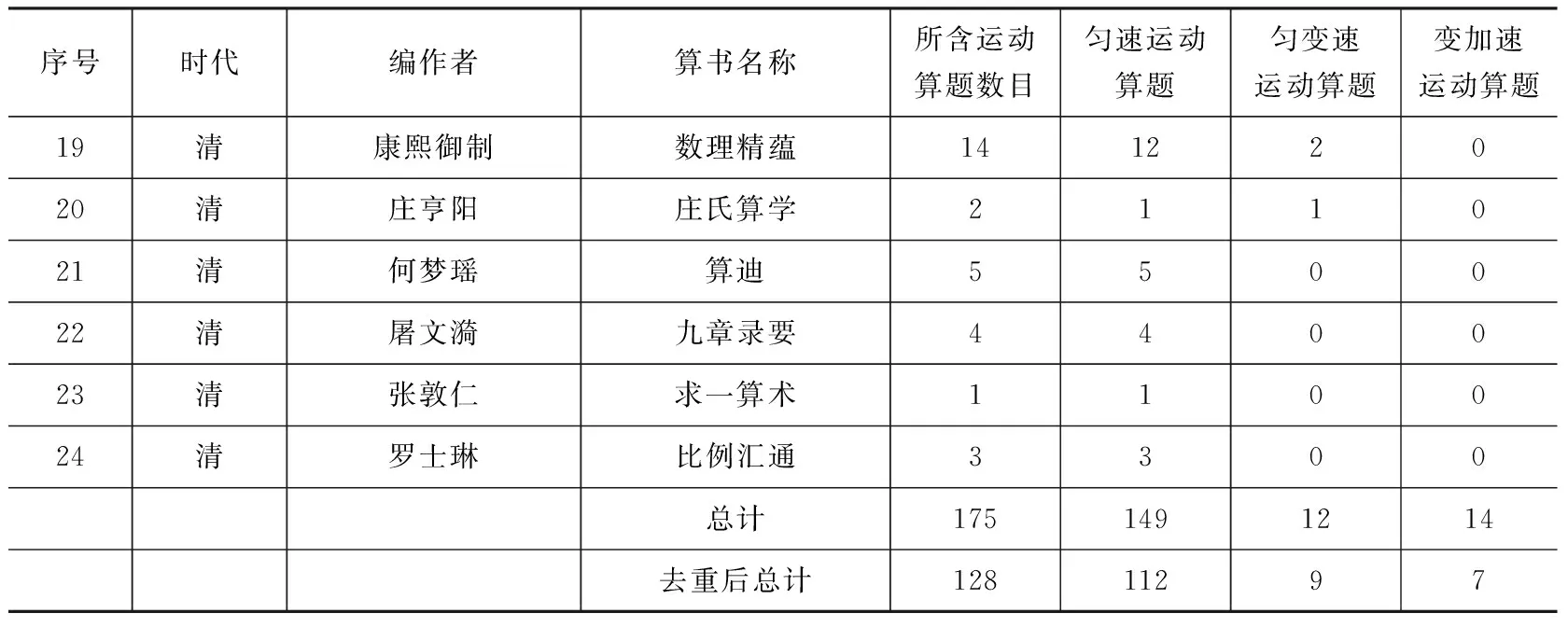
续表1

首先需要说明的是,明末西学东渐开始后,一些西方数学知识得以传入中国。在明末及清代学者撰写的一些会通中西的数学著作中,即包含了一部分西方传入的数学知识。上表中如《数理精蕴》即属这类著作,该书中有16道运动算题,其中2道以“验时仪算炮声”的题目明显受到西学的影响,因此表中未予统计。本文将少数这类著作列为讨论的内容,是因为：这类算书中的运动学算题,内容多是延袭中国传统算题类型,如“重车空车同程往返问题”、“追及问题”等；所运用的也多是中国传统已有的解题方法,即便是所谓“借根方”,也还是中国传统的天元术；而且所讨论的多为相对简单的匀速运动问题,不影响本文的结论。

1 匀速运动问题

这类算题数量最多。虽然同是匀速运动,但针对不同的题设条件和问题情境,古人采用的解题方法也不相同,因此,可以将这类算题细分为以下几种。

1.1 单体匀速运动问题

24部算书中共有12道这类算题,题设条件比较简单,一般是行程、时间和速度三个物理量之间的互算。

第一类：单体单一速度问题

一个物体,以一种不变的速度运动,这是最简单的运动形式。*古算书中的运动学算题,极少考虑速度的方向(仅有《九章算术》“句股”章中两题、《方程论》中一题等少数几题涉及),所以,本文在计算过程中,一般不考虑速度的矢量性。此外,古代算题中,只有少数题的情境可被视作直线运动,如“两鼠对穿”问题、“瓜瓠相向生长”问题等,故仅在这些情况下,将路程称为位移。另外,有一些问题虽然并不是物理学上的运动学问题,但可以用运动学做类比来理解,我们亦纳入进来,比如织布问题等。

例1 张家山汉简《算数书》：

行 甲行五十日,今日壬申。问：何日初行。术曰：问壬申何旬也。曰：甲子之旬也。既道甲数到壬九日,置九,又增(下有缺简)。[8]

因为简文有缺失,已无法得知此题的题解方法。但是,由题设条件可以推断,这应是一个单体运动问题。此题是已知行程时间和到达时刻,求初始时刻。

例2 吴敬《九章算法比类大全》：

三藏西天去取经,一去十万八千程,每日常行七十五,问公几日得回程。

答曰：一千四百四十日。法曰：置(一十万零八千里),以每日(七十五里)为法,除之,合问。[9]*括号内文字为文间夹注,下同。

吴敬的算法是直接用行程除以速度,得所用的时间。

从这类算题的题设条件来看,古人讨论的匀速运动,通常指每日的行程为定值,而非物理意义上绝对的速度大小不变。这类算题除了路程、速度和时间之间的互算,还包括时间单位的换算,要求对于时刻和时间关系的正确理解。

第二类：单体多个速度问题

一个物体在运动过程中的不同时段,会改变速度的大小*在本文讨论的这些算题中,未涉及速度方向的变化。,此即单体多个速度运动问题。

例 《数理精蕴》：

设如一人行路,步行则三十日可到,骑行则二十日可到；今行二十六日到。问：步行、骑行日数各几何？法：以三十日与二十日相减,余十日为一率；步行三十日为二率；今行二十六日,与骑行二十日相较,多六日为三率；推得四率十八日,为步行之日数；与共二十六日相减,余八日,即骑行之日数也。……[10]

《数理精蕴》采用的是比例算法,一率与二率之比,等于三率与四率之比,直接就时间关系进行比较,并未引入速度(日行里数)关系。

物理解法：设步行的速度为v1、时间为t1,骑行的速度为v2、时间为t2,则有联立方程组

即可解得t1=18日,t2=8日。

这类算题共有5道,分别采用了比例算法以及西方传入的借根方法,数学解法与物理解法没有本质的区别。

1.2 两体匀速运动问题

这类算题有82个。按照运动情况及解题方法的不同,两体匀速运动又可以分为“重车空车同程往返问题”、“追及问题”、“相遇问题”等类型。

第一类：重车空车同程往返问题

甲地向乙地运粮,重车去,空车回,重车和空车的行驶速度不同,根据一定时间内的往返次数计算两地间里程。这类算题共有8道。

例1 《九章算术》：

今有程传委输,空车日行七十里,重车日行五十里。今载太仓粟输上林,五日三返。问：太仓去上林几何？答曰：四十八里一十八分里之一十一。

术曰：并空、重里数,以三返乘之,为法。令空、重相乘,又以五日乘之,为实。实如法得一里。

刘徽注云：

此术重往空还,一输再还道。置空行一里,七十分日之一,重行一里用五十分日之一。齐而同之,空、重行一里之路,往返用一百七十五分日之六。完言之者,一百七十五里之路,往返用六日。故“并空、重”者,并齐也；“空、重相乘”者,同其母也。于今有术,五日为所有数,一百七十五为所求率,六为所有率。以此所得,则三返之路。今求一返者,当以三约之。故令乘法而并除,亦当约之也。[11]*本段引文中“程传委输”的“程”字原作“乘”,系据杨辉《详解九章算法》本。此字在戴震辑录本《九章算术》中作“程”。邹大海比较了睡虎地汉简《算术》与《九章算术》及《张丘建算经》中委输算题的异同,并指出《九章算术》委输算题中的重车、空车的日行里数当源于法律中“程”(法律中的数量标准)中的规定,故以作“程”字者为是(邹大海：《从出土竹简看中国早期委输算题及其社会背景》,《湖南大学学报(社会科学版)》,2010年,第4期,第5～10页)。本文采用这一观点。

以v1、v2分别表示重车和空车的速度,以S表示出发地到目的地的距离,重车空车往返3次所花费的时间记为t′(t′=5日),则《九章算术》的解法可直接表达为：

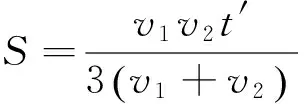
刘徽按语的解法采用“今有术”,即四项比例算法。[12]设重车、空车往返一次路程为S1,所用时间为t1；而用时间t2,可以往返的路程为S2,以“今有术”列出的比例式为：

上式也可以变成：

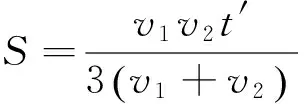
可见,刘徽采用比例算法求解,本质上与《九章算术》相同。

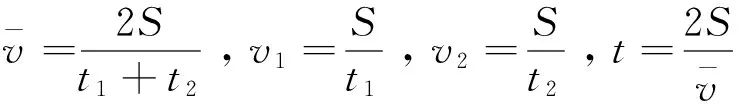
可见,数学解法与物理解法本质上是一致的。

睡虎地汉简《算术》、《张丘建算经》、《九章算法比类大全》及《数学钥》等算书中均有与此类似的算题。

例2 《数理精蕴》：

设如空车一日行三十里,重车一日行二十里,今载米至仓,往返足一日。问：距仓路远几何？法：以空车行三十里,与重车行二十里相乘得六百里,又以重车行二十里乘空车一日得二十日,以空车行三十里乘重车一日得三十日,乃以二十日与三十日相并得五十日为一率,六百里为二率,一日为三率,得四率一十二里,即距仓之里数也。([10],下编卷7,52a～53a)

《数理精蕴》采用的是比例算法,设重车和空车的速度分别为v1、v2,往返两地一次所需的总时间为t,两地距离为S,有比例关系：

本题的物理解法与上一题相同。

由以上两例可看出,对于这类算题,数学解法与物理解法是一致的。

第二类：追及问题

追及问题的基本情境是同向运动的两个物体,慢者先行在前,快者追之在后,二者在不相等的时间内运行了相等的路程。

例1 《九章算术》：

今有善行者行一百步,不善行者行六十步。今不善行者先行一百步,善行者追之。问：几何步及之？答曰：二百五十步。

术曰：置善行者一百步,减不善行者六十步,余四十步,以为法。以善行者之一百步乘不善行者先行一百步,为实。实如法得一步。

刘徽注云：

此术以六十步减一百步,余四十步,即不善行者先行率也；善行者行一百步,追及率。约之,追及率得五,先行率得二。于今有术,不善行者先行一百步为所有数,五为所求率,二为所有率,而今有之,得追及步也。([11],262～264页)

《九章算术》的解法是：

设善行者速度为v1,不善行者速度为v2；经过时间t1,善行者行100步；而经过时间t,善行者追及不善行者,其所行路程为S,则上式等价于：

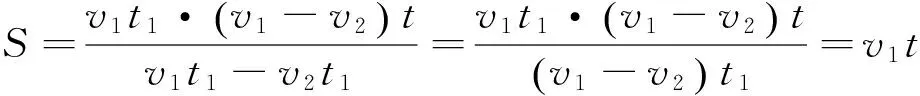
由此也就从物理角度解释了《九章算术》解法的合理性。

刘徽采用的是今有术,即建立如下比例关系：

代入所设物理量,即得：

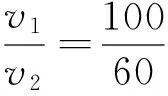
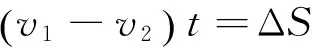
S=v1t。

联立以上三式,即可求解。

比较以上几式可以看出,此题的数学解法与物理解法本质上是一致的。《九章算法比类大全》与《算法统宗》中有与此类似的算题。

例2 《张丘建算经》：

今有人盗马,乘去已行三十七里,马主乃觉,追之一百四十五里,不及二十三里而还。今不还追之。问：几何里及之？答曰：二百三十八里一十四分里之三。术曰：置不及里数,以马主追里数乘之为实,以不及里数减已行里数余为法,实如法而一。[13]

此题的解法用算式表达,即：

设马主的速度为v1,盗马者的速度为v2,从马主开始追击时计时,经过时间t1,不及23里。若“今不还追之”,再经过时间t2,可追及。将各量代入上式,即：

这是一个恒等式。

物理解法：设各物理量如上,已知盗马者先行路程ΔS1=37里,马主追行S1=145里,不及ΔS2=23里,求追及时,马主复行之路程S2。有

S1=v1t1，

v1t1-v2t1=ΔS1-ΔS2，

S2=v1t2，

v1t2-v2t2=ΔS2。

联立方程组,可解得S2=3335/14里。

此题的数学解法与物理解法也是一致的。《透簾细草》、《九章算法比类大全》、《算法统宗》与《数理精蕴》中都有与此类似的算题。

例3 朱世杰《算学启蒙》：

今有良马日行二百四十里,驽马日行一百五十里。驽马先行一十二日。问：良马几何日追及之？答曰：二十日。术曰：列一十二日,以一百五十里乘之,得一千八百里为实,列良驽马日行里数相减,余九十里为法,实如法而一,合问。[14]

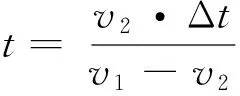
物理解法：设良马和驽马的速度分别v1、v2,驽马先行的时间Δt,驽马先行的路程为ΔS,有关系式

ΔS=v2·Δt，

Δv=v1-v2。

联立方程组,即可求出t。

由表达式可以看出,朱世杰的解法与物理解法是一致的。《数学通轨》、《九章算法比类大全》、《算法统宗》及《数理精蕴》等都有与此题类似的算题。

例4 梅文鼎《方程论》：

假如广、福二船哨海,福船先发行五日,广船行三日遇于中途,其泛地相距二千五百里；遂又同往一岛,广船行四日先至,候六日福船始至。问：各船每日行率？解曰：此广船疾,福船迟也。广船三日,福船五日,共行水面二千五百里。广船四日,福船十日,而水程相当。答曰：广船日行五百里,福船日行二百里。[15]

本题是联立两元一次方程组求解。设福船与广船的速度分别为v1、v2,根据题设条件可以列式如下：

5v1+3v2=2500，

10v1=4v2。

联立以上两式,可解得v1=200里/日,v2=500里/日。

物理解法与此相同。

两体追及类算题共有49道,约占总算题的三分之一。古人采用的数学解法有直接列式、今有术、方程组、盈不足术等。这些数学解法的表达式,都可以被还原为等效的物理表达式。由此说明,这类算题的数学解法与物理解法本质上是一致的。

第三类：相遇问题

相遇问题的基本情境是两个物体的运动时间相同,所行路程不等,二者行程之和为总路程。

例1 《九章算术》：

今有垣高九尺。瓜生其上,蔓日长七寸；瓠生其下,蔓日长一尺。问：几何日相逢？瓜、瓠各长几何？答曰：五日十七分日之五,瓜长三尺七寸一十七分寸之一,瓠长五尺二寸一十七分寸之一十六。术曰：假令五日,不足五寸；令之六日,有余一尺二寸。([11],299～301页)*瓜蔓、瓠蔓的生长并非常见的运动学问题类型,但是本题的题设条件、所求问题仍是基于位移和速度、时间关系来展开讨论的,也正符合运动学的讨论范畴,故本文将之作为运动学问题予以解读。

若对上式进行简单推导,有：

比较两种解法可以看出,对于匀速运动的物体相遇问题,用盈不足术与运用物理学的合速度求解是等效的。

例2 程大位《算法统宗》：

今有大都路至杭州四千二百七十五里,马从大都往南,日行一百二十里；船从杭州往北,日行七十里。问：船、马几日相会,各行若干？答曰：二十二日半(马行二千七百里,船行一千五百七十五里)。法曰：置(四千二百七十五里)为实,却并船、马日行共(一百九十里)为法,除之得(二十二日半)又为实,各以原行里数乘之,得各行数。[16]

物理解法与此相同。《数学钥》、《数理精蕴》及《比例汇通》,都有与此类似的算题。

两体相遇类算题共有25道,由以上二例可以看出,其数学解法与物理解法也是一致的。

1.3 多体匀速运动问题

所谓多体,即参与运动的物体数量大于二,至少有三个物体参与运动。

第一类：多体同速问题

多个物体以相同的速度参与运动,即为多体同速问题。此类算题共有3道。

例 《九章算法比类大全》：

今有织匠二十四人,一百九十二日织纻丝五百七十六匹,欲令六十二人织三百六十日,问该织几何？答曰：二千七百九十匹。法曰：置匠(六十二人)以乘(三百六十日,得二万二千三百二十),以织(五百七十六匹)乘之(得一千二百八十五万六千三百二十)为实；以原织日(一百九十二,得四千六百八)为法。除之合问。([9],222页)

已知24人经192日共织丝576匹,求62人经360日,可织丝多少匹。根据题意,这些织匠织丝的速度是相同的。《九章算法比类大全》的解法为：

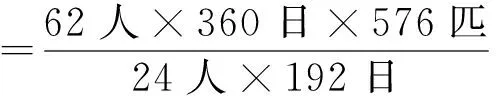
物理解法一般先求出平均每位织匠织丝的速度,再乘以织丝时间和人数,以得到所求织丝长度。虽然先求的物理量有所差别,但此题的数学解法与物理解法本质上是一致的。柯尚迁《数学通轨》中有与此类似的算题。

第二类：多体相遇问题

多个物体同时参与运动,它们的运动时间相同,所行路程不同,各自行程之和为总路程,此即多体相遇问题。此类算题共有5道。

例1 岳麓书院藏秦简《数》：

有妇三人,长者一日织五十尺,中者二日织五十尺,少者三日织五十尺。今威有功五十尺。问：各受几何？曰：长者受廿七尺十一分尺三,中者受十三尺十一分尺七,少者受九尺十一分尺一。术曰：各置一日所织。……[17]

由于此简的术文已经残缺,无法窥见古人的解法。

物理解法：设长、中、少三者的织布速度分别是v1、v2、v3,经过时间t,三者的织布长度分别为L1、L2、L3。已知,v1、v2、v3及织布总长度L,求L1、L2、L3。有关系式：

L1∶L2∶L3=v1∶v2∶v3，

L1+L2+L3=L。

联立方程组,即可解得答案。

例2 张家山汉简《算数书》：

妇织：有妇三人,长者一日织五十尺,中者二日织五十尺,少者三日织五十尺。今织有功五十尺。问：各受几何尺？其得曰：长者受廿五尺,中者受十六尺又十八分尺之十二,少者受八尺又十八分尺之六。其术曰：置一、置二、置三,而各并以为法,又十而五之以为实,如法而一尺。不盈尺者,以法命分。三为长者实,二为中者,一为少者。([8],64～65页)

《算数书》的解法如下：

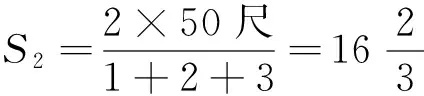
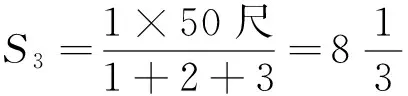
因为三人织布的时间相同,所以织出布的长度应正比于各人织布的速度(长、中、少三者的织布速度之比应为1∶1/2∶1/3)。由此可知,张家山汉简取“三为长者实,二为中者,一为少者”是错误的。*彭浩与郭世荣先生均撰文讨论过张家山汉简《算数书》此题的算法错误。参见彭浩《张家山汉简〈算数书〉注释》(北京：科学出版社,2001年,第64～65页)、 郭世荣《〈算数书〉勘误》(《内蒙古师大学报(自然科学汉文版)》,2001年第3期,第276～285页)。此题的题设与上述秦简《数》的女织题相同,但答案不同。由上一题的物理解答,也可证明汉简的答案及解法是不正确的。

第三类：多体追及问题

多个物体参与运动,各自在不相等的时间内运行了相等的路程,此即多体追及问题。

例 秦九韶《数书九章》：

问军师获捷,当早点差急足三名,往都下节节走报。其甲于前数日申末到,乙后数日未正到,丙于今日辰末到。据供甲日行三百里,乙日行二百四十里,丙日行一百八十里。问：自军前至都里数,及三人各行日数几何？答曰：军前至都三千三百里。甲行一十一日,乙行一十三日四时(半),丙行一十八日二时。术曰：以大衍求之。置各行里,先求总等,存一,约众,得元里。次以连环求等,约奇复乘偶,得定母。以定相乘,为衍母,满定,除衍,得衍数；满定,去衍数,得奇。奇定大衍,得乘率；以乘衍数,得用数。次置辰刻正末,乘各行里,为实；以昼六时约之,得余里。各乘用数,并为总,满衍母,去,得所求至都里,以各日行约之,得日辰刻数。[18]

根据“当早”、“以昼六时约之”可知,三名急足同时自卯初出发,且每日行六个时辰,至申末休息。又由“甲于前数日申末到”,知甲恰行整日数；由“乙后数日未正到”,知乙最后一日行四个半时辰；同理,可知丙最后一日行了两个时辰。所以,总路程S当能被300整除,而除以240当余180里(乙行4.5个时辰的路程),除以180当余60里(丙行2个时辰的路程)。[19]

所以,S满足如下同余式组：

本题的“术文”与“草文”即是用“大衍术”解此同余式组。

物理解法：设甲、乙、丙三人速度分别为v1、v2、v3,三人走完全程L所耗时间分别为t1、t2、t3,设n1、n2分别表示乙较甲多花费的行程天数和丙较乙多花费的行程天数。已知v1、v2、v3及三人到达目的地时的当日时刻T1、T2、T3。求t1、t2、t3,有关系式：

v1t1=v2t2=v3t3=L，

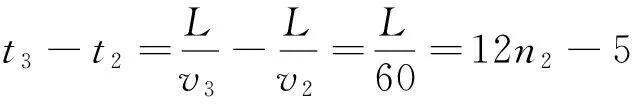
联立化简后,得

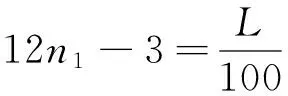
n1、n2均为自然数,L为(100与60的最小公倍数)300的整数倍。上述二式包含三个未知数,所以不能直接联立方程求解,可从n1=1开始试根,得n1=3,L=3300，n2=5。

秦九韶采用的大衍术(即解一次同余式组),在当时是一种数学方法上的创新。物理方法在列出三元一次不定方程后,受已知条件限制,也不能直接求解,只能采用更为基础的试根法。

对于这类算题,古代算法与今日一般物理解法的主要差别体现在逻辑思路上,前者是将运动者的日数关系转换为行程除以速度之后的余数关系,后者则没有对余数关系特别关注。在具体的运算过程中,两种不同思路引起的差别表现为解一次同余式组与解多元一次不定方程的区别。不过,从本质上看,数学算法与物理解法是相同的。

多体追及问题共有6道算题,包括《张丘建算经》中2题、《数书九章》中2题、《方程论》与《求一算术》中各1题。其中,《张丘建算经》与《方程论》中的3题属于匀速圆周运动,本文不予讨论。其余3题,古人都是采用大衍术求解,物理解法是列出多元一次方程组,用试根法解出结果。

为了讨论问题方便,本文将匀速运动算题分为以上几类。事实上,古算书中的匀速运动算题类型丰富,以上几种分类并不能包含所有的内容,限于篇幅,于此不再讨论。

由上述举例分析可见,对于匀速运动问题,无论是单一物体还是多个物体同时参与运动,无论是追及问题还是相遇问题等等,古算书中采用的种种解法,尽管思路不同、途径各异,但本质上与物理解法基本上是一致的。不过,从物理概念看,有些数学解法尽管得出的数值是正确的,但存在量纲错误。

2 匀变速运动问题

匀变速运动是加速度保持不变的运动,包括匀加速、匀减速运动。24部算书中有9道这类算题。根据问题的复杂程度,可将这些算题分为单体运动和两体运动两种类型。

2.1 单体匀变速运动问题

有7道单体匀变速运动算题,其中《张丘建算经》中的两题最为典型。

例1 《张丘建算经》：

今有女善织,日益功疾。初日织五尺,今一月日织九匹三丈。问：日益几何？答曰：五寸二十九分寸之十五。术曰：置今织尺数,以一月日而一,所得,倍之。又倍初日尺数,减之,余为实。以一月日数初一日减之,余为法,实如法得一。([13],卷上,19b～20a)

这是匀加速直线运动问题,已知第1日的位移和前30日的总位移,求加速度。将织布的长度等效为位移,设为S,织布的时间设为t,织布的速度设为v,加速度为a。可将《张丘建算经》的解法表达成算式：

上式的量纲不符合物理要求,对之进行处理,可得：

此式可用物理符号表达为：

以上处理过程,虽然没有改变原来表达式的数值大小,但却改变了其物理意义。从物理上看,《张丘建算经》的解法存在量纲错误。

比较数学解法与物理解法可以看出,虽然二者得到的表达式相同,但前者的物理概念不清楚,存在量纲错误。

例2 《张丘建算经》：

今有女子不善织,日减功迟。初日织五尺,末日织一尺,今三十日织讫。问：织几何？答曰：二匹一丈。术曰：并初、末日织尺数,半之,余以乘织讫日数,即得。([13],卷上,20a～20b)

物理解法：设第i(i=1,2,3…,30)日的织布长度为Si,第i日织布的初速度为vi-1,加速度为a,30日织布总长度为L。已知S1、S30,求：L,有

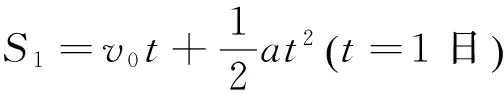
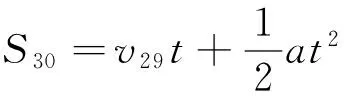
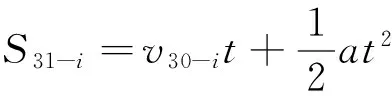
v0+v29=vi-1+v30-i。

联立上述方程,可得

S1+S30=Si+S31-i。

所以,

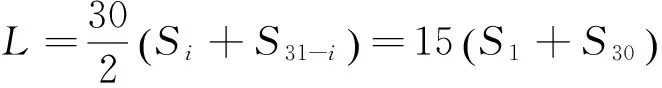
上式中,S1、S30分别代表首末两日的织布长度。因此,上式与《张丘建算经》的解法表达式形式相同。

《张丘建算经》的解法,是建立在对满足等差关系的一组数值求和规律的认识基础上,直接列式求解,较物理方法更为简便,但物理概念不够清晰。两种方法的思路不同,关注的对象也不尽相同。

2.2 两体匀变速运动问题

在24部算书中,仅《九章算术》与《算学宝鉴》中各有1道这种算题,且后者题设条件及所求问题均与《九章算术》相似。

例 《九章算术》：

今有良马与驽马发长安,至齐。齐去长安三千里。良马初日行一百九十三里,日增一十三里,驽马初日行九十七里,日减半里。良马先至齐,复还迎驽马。问：几何日相逢及各行几何？答曰：一十五日一百九十一分日之一百三十五而相逢,良马行四千五百三十四里一百九十一分里之四十六。驽马行一千四百六十五里一百九十一分里之一百四十五。

术曰：假令十五日,不足三百三十七里半。令之十六日,多一百四十里。以盈、不足维乘假令之数,并而为实。并盈、不足为法。实如法而一,得日数。不尽者,以等数除之而命分。求良马行者：十四乘益疾里数而半之,加良马初日之行里数,以乘十五日,得良马十五日之凡行。又以十五日乘益疾里数,加良马初日之行。以乘日分子,如日分母而一。所得,加前良马凡行里数,即得。其不尽而命分。求驽马行者：以十四乘半里,又半之,以减驽马初日之行里数,以乘十五日,得驽马十五日之凡行。又以十五日乘半里,以减驽马初日之行。余,以乘日分子,如日分母而一。所得,加前里,即驽马定行里数。其奇半里者,为半法,以半法增残分,即得。其不尽者而命分。([11],312～317页)

古人定量表达速度的大小,通常是以日行里程的多少而言。所以,本题从数学角度看是等差数列问题；从物理角度看,则是匀变速运动问题。

《九章算术》求相逢日数的算法,采用“盈不足术”,得：

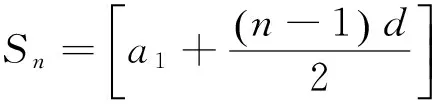
又“以十五日乘益疾里数,加良马初日之行”,得到良马第16日的最大行程(在行完一日的情况下)：

a16=a1+15d=193里+15×13里=388里。

刘徽解法给出的是等差数列求和公式的另一表达形式：*因受限于篇幅,本文将刘徽按语略而未引,相关详细讨论可参见文献[11],313～317页。

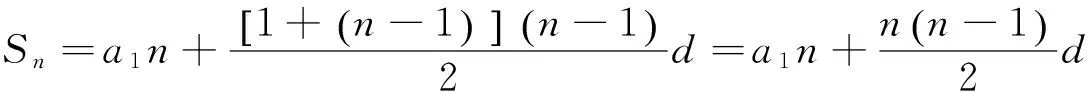
本题是一个非线性问题,《九章算术》和刘徽给出的答案都是近似的。

L+L′=2S，

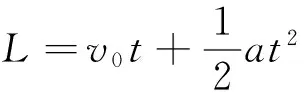
vt=v0+at，

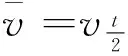
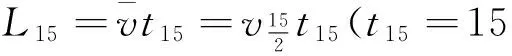
从概念上看,此题的数学解法与物理解法有本质区别,将《九章算术》解法得出的等差数列求和公式与物理学的匀加速运动公式进行比较,更容易看出两种解法的差别,具体见表2。

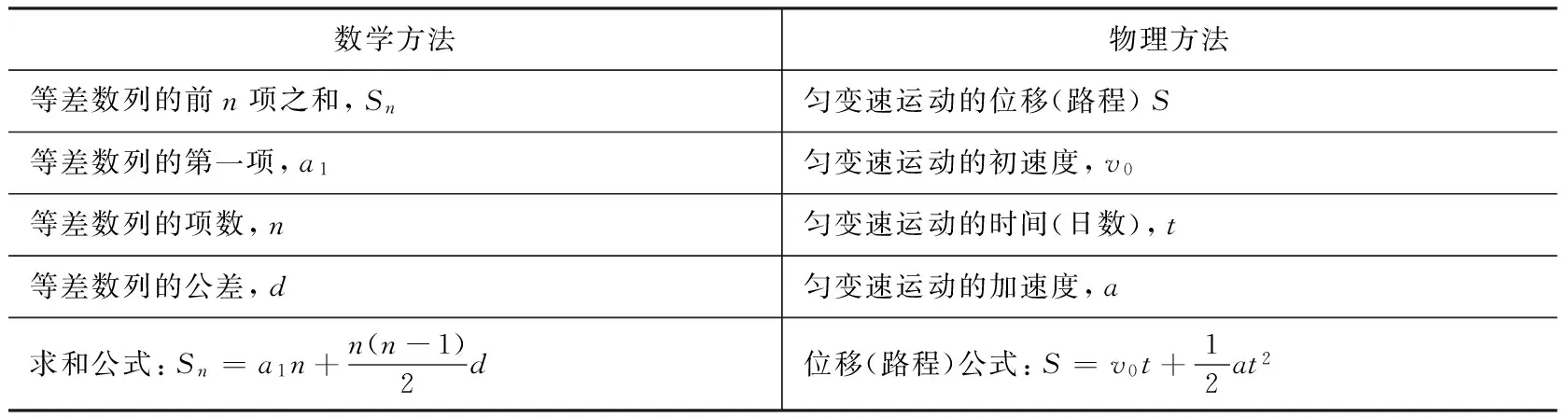
表2 处理匀变速运动的一般数学方法与物理方法比较

由上表可见,数学方法中的Sn、n、d分别与物理方法中的S、t、a在数值上对应相等,而数学方法中的a1,对应物理方法中第一日的路程S1：

这说明,对于匀变速运动,在特定的情况下,数学的等差数列求和公式可以过渡到物理的匀变速运动公式。

由上述分析可见,对于匀变速运动问题,数学解法与物理解法的差别,除了解题思路、物理概念不同之外,所运用的公式也不同,前者用的是等差数列公式,后者用的是匀变速运动公式。尽管在特殊情况下,两种解法的表达式可以化为一致,但物理概念并不是一回事。

3 变加速运动问题

变加速运动不仅速度是变化的,加速度也是随着时间而变化的。在物理学中,求解这类算题需要运用高等数学的微积分方法。古算书中有7道这类算题,本文将之分为单体运动和两体运动予以讨论。

3.1 单体变加速运动问题

例1 《九章算术》：

今有女子善织,日自倍。五日织五尺,问：日织几何？答曰：初日织一寸三十一分寸之十九,次日织三寸三十一分寸之七,次日织六寸三十一分寸之十四,次日织一尺二寸三十一分寸之二十八,次日织二尺五寸三十一分寸之二十五。术曰：置一、二、四、八、十六为列衰；副并为法；以五尺乘未并者,各自为实,实如法得一尺。([11],100页)

据题设条件,每日织出新布的平均速度是按等比级数增大的,所以,此题可看作单体变加速直线运动问题。

《九章算术》的解法是“置一、二、四、八、十六为列衰”,即将之视为一至五日各日织布长度的比例关系,也即每日新出布匹的位移比例关系。五日共织布五尺,那么第一日织布的长度即为

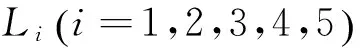
v1∶v2∶v3∶v4∶v5=1∶2∶22∶23∶24。

由关系式

L=vt,

v1·t+2v1·t+22v1·t+23v1·t+24v1·t=5尺，

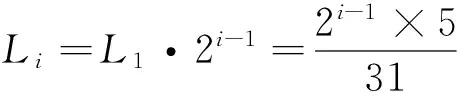
这个结果与数学解法相同。张家山汉简《算数书》及《孙子算经》都有与本题相似的算题。

例2 《张丘建算经》：

今有马行转迟,次日减半,疾七日,行七百里。问：日行几何？答曰：初日行三百五十二里一百二十七分里之九十六,次日行一百七十六里一百二十七分里之四十八,次日行八十八里一百二十七分里之二十四,次日行四十四里一百二十七分里之一十二,次日行二十二里一百二十七分里之六,次日行一十一里一百二十七分里之三,次日行五里一百二十七分里之六十五。术曰：置六十四、三十二、一十六、八、四、二、一为差；副并为法；以行里数乘未并者,各自为实,实如法而一。([13],卷下,2b～4a)

此题的运动对象与上一题不同,但本质上没有区别。从数学上看,两题都是等比数列问题,已知公比、项数及数列的和,求每一项的值。

从物理学看,这是一道加速度为负的变加速运动问题,解法与上一题相同。《九章算法比类大全》中有1道算题与本题相似。

24本古算书中共有5道这类算题。对于这种类型的单体变加速运动问题,数学解法与物理解法都是关注每日行程大小的比例关系。也即,两种方法的基本思路及解题结果都是一致的。

3.2 两体变加速运动问题

例1 《九章算术》：

今有蒲生一日,长三尺；莞生一日,长一尺。蒲生日自半；莞生日自倍。问：几何日而长等？答曰：二日十三分日之六,各长四尺八寸一十三分寸之六。术曰：假令二日,不足一尺五寸；令之三日,有余一尺七寸半。([11],301～303页)

从数学上看,这是一道等比数列求和问题。《九章算术》采用盈不足术求解,代入“盈不足术求不盈不朒之正数公式”*关于盈不足术求不盈不朒之正数公式的介绍,参见文献[11],292页。,得：

由于盈不足术在求解非线性问题上的局限性,本题只能得出近似解。*关于盈不足术在求解非线性问题上的局限性的讨论,参见钱宝琮《中国数学史话》(北京：中国青年出版社,1957年,第32～35页)。

从物理学来看,这是(一维)变加速直线运动问题。蒲的生长长度S与时间t的函数关系为[20]：

莞的生长长度S′与时间t的函数关系为：

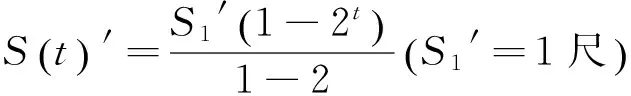
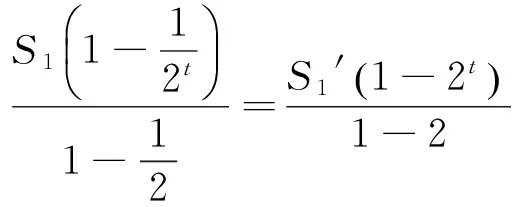
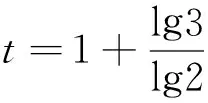
例2 《九章算术》：

今有垣厚五尺,两鼠对穿。大鼠日一尺,小鼠亦日一尺。大鼠日自倍,小鼠日自半。问：几何日相逢？各穿几何？答曰：二日一十七分日之二。大鼠穿三尺四寸十七分寸之一十二,小鼠穿一尺五寸十七分寸之五。术曰：假令二日,不足五寸；令之三日,有余三尺七寸半。([11],320～322页)

此题与上一题同属一维变加速运动问题。两题的相同之处在于速度变化的规律相同,两个速度一增一减,都是呈等比级数变化,且两个公比互为倒数；不同之处只是在对于两个初速度具体数值以及行程关系的设定上。

《九章算术》采用盈不足术求解,得：

此解亦为近似解。

物理解法：可以列出大鼠的位移S与时间t的函数关系为：

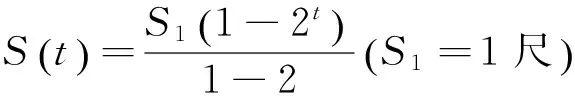
小鼠的位移S′与时间t的函数关系为：

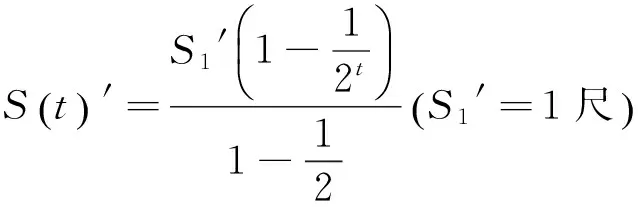
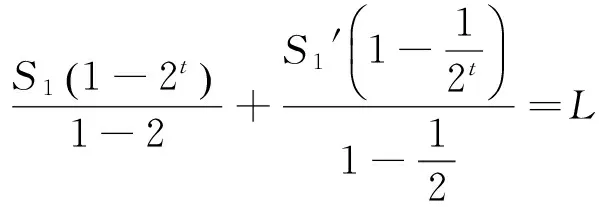
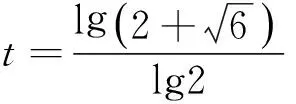
对于单体变加速运动问题,数学解法与物理解法的基本思路是一致的,得出的表达式也是一样的。但对于上述《九章算术》所列的两体变加速运动问题,两种解法则有很大区别。数学解法运用盈不足术,得出的是近似解。物理解法是建立时间与路程的函数关系,得出的是非线性方程,运用微积分方法可以得出精确解。

4 讨论与结论

基于上述数学解法与物理解法的分析比较,可以得出如下一些初步的认识：

其一,中国古代很早就习惯于运用比例方法求解运动学问题,这种做法是成功的。

早在先秦或秦代,中国学者已经运用比例方法解决运动学问题*比如,针对睡虎地汉简《算术》中的委输问题,邹大海复原了古人推导算法的方式,并证明这类问题和算法早在战国时秦国(至迟在秦代)就已经出现。参见邹大海《从出土竹简看中国早期委输算题及其社会背景》(《湖南大学学报(社会科学版)》,2010年第4期,第5～10页)。,3世纪刘徽则记录了有关算法的推导。事实证明这种方法是成功的。原因有二：一是他们求解的是纯运动学问题,即只探讨运动过程,而不涉及导致运动状态发生改变的原因——力的问题；二是他们运用比例方法解决的都是匀速运动问题,对于这种运动,速度、时间、位移之间是满足一定的比例关系的。

古希腊亚里士多德最先运用比例方法探讨运动学问题。他假设A为推动者,B为运动者,Г为被通过的距离,Δ为所经过的时间,认为在相等的时间里,相等的力A将会使半个B通过2个Г的距离,而在半个Δ的时间里使半个B通过1个Г的距离,因为这样是合比例的。[21]

中世纪后期,列奥纳多·达芬奇继续运用亚里士多德的比例方法研究运动学问题。他在《笔记》中写道：“如果一个力使某重物在某段时间内运动一段距离,那么同样的力在相等的时间内使一半重的物体移动两倍的距离,或者这个力使物体在一半时间内运动一半的距离,或者这个力在相等的时间内使两倍重的物体运动一半的距离”；“或者相同大小的力,在一半的时间内将一半大小的物体移动相等的距离。”但是,达芬奇发现,运用这种方法会导致显而易见的荒谬结果：“这个力在1倍的时间内将1倍大小的物体移动相等的距离,在1000倍的时间内将1000倍大小的物体移动相等的距离。”[22]

亚里士多德和达芬奇运用比例方法研究运动问题,探讨力与运动的关系,属于动力学研究传统。事实上,在尚不能定量地表示力的情况下,运用比例方法研究力与运动的关系是行不通的。

其二,对于一些复杂的运动学问题,数学解法与物理解法具有本质的区别。

对于匀速运动,数学解法与物理解法基本上是一致的,二者没有本质差别。

对于匀变速运动,数学解法与物理解法除了解题思路不同之外,所运用的公式也不同,前者用的是等差数列公式,后者用的是匀加速运动公式。这种差别反映了两种解法具有本质的不同。

对于单体变加速运动,数学解法与物理解法思路一致,得出的表达式也是一样的。但对于《九章算术》所列的两体变加速运动问题,从数学上看,是等比数列求和问题；从物理学看,是变加速直线运动问题。数学解法运用盈不足术,得出的是近似解。物理解法是建立时间与路程的函数关系,得出的是非线性方程,运用微积分方法可以得出精确解。因此,这两种解法具有本质差别。

其三,中国古人虽然对一些运动学问题已有清醒的认识,但并未形成一般性的物理概念。

速度是运动学的一个基本概念。《管子·乘马》称：“有一宿之行,道之远近有数矣。”《九章算术》用“一日行若干路程”表示速度。可见中国古人在处理具体的运动问题时,很早即有了速度观念,但始终未能提出作为一般概念的“速度”一词。

《九章算术》中良马“日增一十三里”,驽马“日减半里”；《张丘建算经》中“今有女善织,日益功疾”,“今有女子不善织,日减功迟”。这些都表示了对匀变速运动的认识。

《九章算术》中“今有女子善织,日自倍”、“蒲生日自半、莞生日自倍”、“大鼠日自倍,小鼠日自半”和《张丘建算经》中“今有马行转迟,次日减半”，都表达了对变加速运动的认识。

《九章算术》中的良马、驽马算题,术文将良马“日增一十三里”称为“益疾里数”。这即是对加速度的称谓。

这些都表明,中国古人对匀速运动、匀变速运动及变加速运动现象都有清醒的认识,只是没有形成一般性概念。

中世纪,欧洲的经院派学者开始研究运动学问题。13世纪上半叶,巴黎大学杰拉尔德(Gerard of Brussels)著有《论运动》(BookonMotion),开创了有别于亚里士多德的运动学研究传统。14世纪上半叶,牛津大学默顿学院的几位学者提出了速度和瞬时速度概念,区分了匀速运动和非匀速运动,定义了匀加速运动,提出了平均速度定律(也称“默顿规则”)。[23]之后,意大利奥雷姆(Nicole Oresme)把默顿学派的平均速度定律用几何图形表示出来,并由图形发现：初速度为零的匀加速运动物体在前一半时间内所走过的距离,是后一半时间走过距离的三分之一。17世纪上半叶,伽利略继承和发展了中世纪的运动学研究传统,提出了匀加速运动定律。再后,牛顿综合运用动力学和运动学两种研究传统,建立了经典力学体系。

中世纪,欧洲学者研究运动学问题,采用的是抽象的逻辑推演方法。他们认为,如果现实中存在匀加速运动,那么,“默顿规则”就可以运用到这种运动中。至于现实中哪些运动属于这种运动,他们并不关心。从具体现象提炼出一般概念,归纳出一般性问题,经过推演,得出一般性结论。这是西方人惯用的思维方式和研究方法。

与欧洲人相比,中国古人不乏处理具体问题的经验和技巧,但不善于从经验中提出普遍问题,上升为一般性理论。

其四,中国古人对运动现象的认知方式是数学性的,而非物理性的。

古人把物理运动学问题看作数学问题,用数学方法求解。虽然对于一些简单的运动问题,数学解法与物理解法本质上是一致的,但数学解法的物理概念不够清晰,有些算题存在物理量纲错误；对于一些比较复杂的运动学问题,古人得出的结果是数学公式,无法将其还原为物理公式,此即体现了数学解法的本质特征。由于古人把物理问题看作数学问题,而且局限于解决具体问题,因而不能提出一般性物理概念,提炼出一般性物理问题,长期停留在一个认识水平上,无法发展成一般的运动学理论。这是古代数学解法无法走向物理运动学的根本原因。另外,古代的运动学算题习惯于以“日”作为时间单位,而没有采用“秒”之类的更为精确的时间计量单位,因而不可能对运动过程中物体速度的变化情况做出精确的描述,这也是其无法走向物理运动学的原因之一。不过,必需看到,中国古人早在汉代即能近似求解一些比较复杂的运动学问题,并且具有一些清晰的认识,这在世界物理学史上仍然是一项突出的成就。

最后尚需说明,算书关注的是数量关系及算法,古代算学家把现实中的运动现象提炼成数学问题予以解答,这是值得充分肯定的科学成就。我们没有理由要求古代算学家一定要以物理的视角看待运动学问题。本文的目的绝非要苛求古人,而是要分析、比较面对同一种认识对象,传统数学认知方式与西方物理认知方式的异同,进而探讨中国传统的认知路线无法走向物理运动学的原因。

致 谢 第一位审稿人指出,中国古代运动学算题以“日”作为时间单位,而不是以精确的“秒”为单位,这也是其无法走向运动学的原因。本文吸收了这一见解,特此表示感谢。此外,韩琦先生与邹大海先生也对本文提出了重要的修改意见,在此一并致谢。

1 戴念祖,卫中,汪达开. 以物理学观点评中国古代数学著作[J]. 自然科学史研究,1997,16(2)：161～173．

2 吴文俊主编,沈康身分卷主编. 中国数学史大系. 第2卷[M]. 北京：北京师范大学出版社,1998：407．

3 周靖. 17世纪中前期中国和西方对加速度的认识[J]. 淮阴师专学报,1997,19(5)：38～41．

4 周靖,吴立飞. 中国古代对变速运动的认识[J]. 淮阴师范学院学报(自然科学版),1999,24(4)：45～49．

5 周靖. 中西方古代对直线加速运动的认识差异浅析[J]. 淮阴师范学院学报(自然科学版),2004,(1)：40～44．

6 李伯川,化存才,赵奎奇.《九章算术》中的运动学题例剖析[J]. 云南农业大学学报,2012，(6)：118～122．

7 陈育成.《九章算术》中的“物理题”赏析[J]. 青年时代,2014，(10)：13．

8 彭浩. 张家山汉简《算数书》注释[M]. 北京：科学出版社,2001．

9 吴敬.九章算法比类大全[M] //中国科学技术典籍通汇.数学卷(二). 郑州：河南教育出版社,1993．

10 御制数理精蕴[M]. 康熙内府铜活字印本．

11 郭书春. 《九章算术》译注[M]. 上海：上海古籍出版社,2009．

12 白尚恕. 《九章算术》与刘徽的今有术[C] //吴文俊. 《九章算术》与刘徽. 北京：北京师范大学出版社,1982. 246～255．

13 张丘建著,甄鸾等注,刘孝孙细草. 张丘建算经[M]//宋刻算经六种. 北京：文物出版社,1981．

14 朱世杰. 算学启蒙·卷中[M]. 罗士琳校勘扬州刻本.16.

15 梅文鼎. 方程论·卷5[M] //历算全书. 咸丰九年青珊瑚馆刊本.4a～4b．

16 程大位. 新编直指算法统宗[M] //续修四库全书.第1044册. 上海：上海古籍出版社,2002.145．

17 朱汉民,陈松长. 岳麓书院藏秦简(贰)[M]. 上海：上海辞书出版社,2011. 18,98～99．

18 秦九韶. 数书九章·卷2[M]. 上海：商务出版社,1937. 34～38．

19 吴文俊主编,沈康身分卷主编. 中国数学史大系[M]. 第5卷. 北京：北京师范大学出版社,2000. 358～361．

20 (美)赛维(R. A. Serway)著,汤发宇译. 普通物理学概念及程序练习(上册)[M]. 北京：人民教育出版社,1979. 20～21．

21 亚里士多德著,张竹明译. 物理学[M]. 北京：商务印书馆,1997. 214～215．

22 MacCurdy E.TheNotebooksofLeonardodaVinci,ArrangedandRenderedintoEnglish[M]. VolumeⅠ. London：Jonathan Cape Ltd,1977. 483,510．

23 Lindberg D C.TheBeginningsofWesternScience[M]. Chicago：The University of Chicago Press, 1992. 294～295．

A Comparison of the Solutions of Traditional Mathematics and Modern Physics of Computational Problems related to Kinematics in Pre-modern Chinese Mathematical Books

HU Huakai, ZHANG Yangyang

(Dept.ofHistoryofScience,UniversityofScienceandTechnologyofChina,Hefei230026,China)

There are about 175 computational problems related to kinematics in at least 24 of the mathematical texts dating from the Qin Dynasty to the middle of Qing Dynasty. These questions cover uniform motion, uniformly accelerated motion and accelerated motion. While different to modern kinematics, not only in problem solving and cognitive methods, but also in knowledge system, pre-modern Chinese used many kinds of mathematical methods to solve these problems. By systematic analysis and comparison of the solutions of traditional mathematics and modern physics of such computational problems, it is found that the solutions of traditional mathematics are consistent with those of modern physics in the problems of uniform motion, while these two kinds of solutions are inherently different in some more complex problems of uniformly accelerated motion and accelerated motion. This reflects a unique physical cognitive style and problem solving method. The pre-modern Chinese cognitive style of the phenomenon of object motion is mathematical rather than physical. Therefore, no general physical concepts were raised and no general physical problems extracted, a cognitive level that remained over a long period, preventing the development of a general kinematics theory．

pre-modern Chinese mathematical books, kinematics problems, mathematical solutions, physics, comparison

2015- 12- 15；

2016- 01- 03

胡化凯,1954年生,安徽蒙城人,博士,教授；张阳阳,1987年生,安徽滁州人,博士研究生。

N092∶O112

A

1000- 0224(2016)02- 0127- 23