全相位与Geiger算法的岩石声发射源定位方法*

黄晓红，孙国庆，张凯月

（1.华北理工大学信息工程学院，河北唐山063009；2.华北理工大学电气工程学院，河北唐山063009）

全相位与Geiger算法的岩石声发射源定位方法*

黄晓红1*，孙国庆2，张凯月1

（1.华北理工大学信息工程学院，河北唐山063009；2.华北理工大学电气工程学院，河北唐山063009）

Geiger定位算法在岩石定位分析中得到广泛应用，但是对初始值要求非常严格，若初始值选择不当，则很难进入收敛范围。为了提高定位精度，减少迭代次数，针对这些问题，提出全相位与Geiger算法的岩石声发射源定位方法。首先进行花岗岩（50 mm×100 mm×50 mm）断铅实验，接着充分利用全相位FFT相位不变性的优势分析断铅信号，通过相位差法求出时延同时反演声发射源求出Geiger迭代初始值，最后综合最小二乘法与Geiger算法，迭代求出最优解。实验仿真结果显示此算法的平均误差相比美国PCI-2型声发射仪器定位结果降低了约5 mm，有效解决了Geiger初始值选取的问题，能够迅速进入收敛范围，提高了收敛速度和定位精度。

信号分析；声发射源定位；全相位相位差；Geiger；最小二乘法；

在一般情况下，由于受力或其它作用下，材料产生瞬间弹性波的现象被称为声发射AE（Acoustic Emission）。

目前对于岩石类材料破坏研究采用的主要手段仍是声发射技术。最常用的定位技术为时差定位，定位的方法主要有：相对定位法、Geiger定位方法、最小二乘法等。在20世纪60年代晚期，Mogi［1］最早在岩石弯曲变形条件下，开始了二维声发射定位研究。之后Scholz［2］进行了声发射事件的三维空间定位研究。胡新亮［3］等利用相对定位法研究了非完整岩体破裂机理，使声发射定位结果的可靠性与精度有所提高。赵兴东［4］等应用声发射定位方法，研究了不同岩石破裂过程的AE活动规律，应用Geiger定位算法对完整岩石失稳破坏过程进行了研究，得到较高定位精度。康玉梅［5］等针对三维定位中初始值选取影响定位精度的问题，即提出了将最小二乘法与Geiger算法结合的定位方法，有效提高了算法的收敛速度，但精度有所不足。张会新［6］等为了获取传感器节点的位置信息，采用TDOA定位算法，并在基础上进行了优化，大大简化了计算量。杨文铂［7］等为了提高无线传感器网络的节点定位精度，通过研究信道噪声，对测量误差进行了修正，提高了定位精度。黄晓红［8］等针对岩石力学声发射时差定位算法中时延估计精度的问题，提出了在全相位相位差法基础上求时延估计的新方法，即利用全相位得到时间差，然后结合最小二乘法得到定位坐标，此方法大大加快了收敛速度，但定位精度有所不足。为了得到更好的定位效果，考虑到Geiger的良好的定位特性，于是在此基础上提出全相位与Geiger算法的岩石声发射源定位方法。

1 全相位与Geiger算法的岩石声发射源定位方法

1.1 基于全相位相位差时延估计法的岩石声发射源定位研究

全相位相位差时延估计法是通过小波分析与全相位频谱分析相结合求解相位差，从而得到声发射信号的时延估计，进而利用时差定位法反演声发射源，实现精确的定位。其中全相位FFT频谱［9-10］分析可测任意含有一个或多个频率的正弦波信号的取样点的相位，从而具有很大优势。通过全相位相位差法得到时间延迟，其推导过程如下：

设s1(k)是AE信号，n1(k)和n2(k)表示随机噪声，Δij为待估计的时间延迟，也就是信号到达第i个传感器和第j个传感器的传播时间差；α为比例系数，则两个空间分开的传感器的接收信号的离散形式分别为：

x1(k)和x2(k)为离散谱线，利用全相位频谱分析方法［5］求信号主谱线频率为k0时的相位分别为：

时间延迟为：

式中，fc代表主谱线频率，fs代表采样频率。

定位算法采用最小二乘法［11］，最小二乘法通过构造残差平方和，以模型参数估量为变量，当函数值达到最小时，即可得到参数估计值的取值。其最大的优势为具有良好的估计特性。公式如式（6）：

式中，x，y，z为试验点坐标；t为事件发生时刻；ti代表波到达第i个传感器的时间；xi,yi,zi为第i个传感器的位置；要得到最终定位结果，理论上至少需要四个传感器，得到三组方程，进行联立求解。定位原理及实现同样是先在各向同性的介质中建立恰当的坐标系，其三维算法模型如下：

分别是四个传感器的坐标，设G点为AE源，坐标为G（x，y，z）。

式中，xi,yi,zi代表第i个传感器的位置坐标，v为波速，试验测得花岗岩样品中的P波波速为3 128.023 5 m/s（波速获得途径通过美国物理声学公司（PAC）PCI-2机器，具体操作方法参考其操作说明，相关声速测试原理见文献［12］）；Δij为AE信号从G点到达第i个传感器和第j个传感器的时间差，综合方程组求解，方可求出AE源G点的坐标。

综合式（7）～式（9），即可求出声发射源坐标，我们把此结果作为下面Geiger迭代初始点。

1.2 基于全相位相位差的Geiger优化迭代算法

Geiger定位方法［13］在地震学领域得到广泛应用，它是在给定初始点的基础上，通过数次迭代来逼近最终结果。此处通过最小二乘法计算修正量，每次迭代都是以此修正量为基础，把向量加到上次迭代结果上，就可以得到一个新的迭代点，判断新点是否满足要求，如不满足，继续迭代。每次迭代的结果由方程式（10）产生。

式中：x，y，z为人为设定的试验点初始值；t为事件发生时刻；ti代表波到达第i个传感器的时间；xi,yi,zi为第i个传感器的位置；v为波速。

设第i个传感器测到的波到达时间为to,i，用试验点坐标计算出的到达时间的一阶泰勒展开式为：

式中：tc,i为由试验点坐标计算出的波到达第i个传感器的时间。

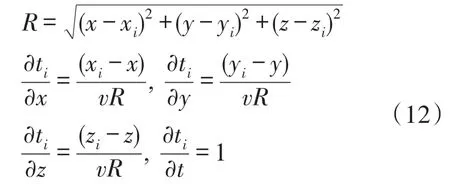
对于N个传感器，矩阵形式表示为：

其中：

求解式（13）就得到修正向量：

之后，以(θ+Δθ)为试验点继续迭代，直至满足Δθ＜φ（这里Δθ为修正量，φ为一小量）。试验中设定本次迭代结果中Δt（式（13）中）值与上次Δt值的差值，即 φ(t)=Δtn-Δtn-1≤10-4，当 φ(t)＞10-4数量级时，迭代结束。由于Geiger初始值一般选取几个传感器包围的中心点坐标，这样选取极容易受传感器位置的影响，所以结合相位差法，选择式（7）～式（9）中结果作为初始迭代值会使最终定位精度更精准。黄晓红等提出的基于相位差时延估计法是对同一主频的子带信号做全相位频谱分析，从而得到每个子带信号的中间点相位，再依据相位差［14］与时间差的关系，分别求出AE信号到达不同传感器之间的时间差，如式（5），进而结合最小二乘法算法求解，实现了声发射源更精确的定位。基于全相位相位差法的Geiger优化迭代算法则是利用全相位相位差法结合最小二乘法求解，从而得到最优初始迭代点，然后利用Geiger迭代法迭代计算，将全相位相位差法和Geiger算法结合使用，能够迅速进入收敛范围，仅需几次迭代就能够迅速收敛。此算法最大优势即省去寻找最优步长的大量时间，加快求解速度，缩短了计算时间，提高了定位准确度。

2 实验分析

试验样品为花岗岩，试件尺寸加工为50 mm× 100 mm×50 mm，加工机器采用DJ-4型自动岩石切割机。声发射系统采用PCI-2型声发射测试分析系统（美国物理声学公司PAC）。传感器型号为R6a型，谐振频率是90 kHz，频率范围35 kHz～100 kHz。声发射系统的门槛值设定为40 dB；前置放大器型号为2/4/6，其频带范围为20 kHz～1 200 kHz；采样频率为2 MHz。为减小传感器自身不可避免的误差，耦合剂用凡士林，将探头耦合在岩样上。本试验中放置的8个传感器的坐标分别为A1（25，80，0）、A2（25，20，0）、A3（50，80，25）、A4（50，20，25）、A5（25，80，50）、A6（25，20，50）、A7（0，80，25）、A8（0，20，25），单位为mm。8个传感器的坐标如表1所示。

表1 传感器布置坐标

试验中，首先确定传感器的安装位置，然后以此点为圆心以传感器为半径，画圆，布置传感器使其和圆形区域高度重合，保证传感器中心点和安放位置中心点吻合。试验共做了10个坐标点（25，60，50）、（25，45，50）、（50，60，25）、（50，45，25）、（25，60，0）、（25，45，0）、（0，60，25）、（0，45，25）、（25，100，35）、（25，100，15）的断铅试验。对试验中8个传感器获取的AE信号分别进行小波去噪处理和小波分解，比较分解后的子带信号，找到每个传感器中主频最接近的4个子带信号，然后进行全相位频谱分析，分别找到主频对应的相位（对于全相位频谱分析而言，主频位置对应的相位即截取信号中间样点的相位），利用相位差法进行时间差测量，结合最小二乘法进行定位，确定初始迭代试验点的坐标，最后用Geiger算法迭代求解，求出最优解。图1列举在坐标点（50，45，25）处进行断铅实验，8个传感器采集到的信号和小波分解第5层细节信号频谱图。表2为8个传感器接收到的信号以及小波分解后子带的信号主频。表3为美国生产PCI-2型声发射仪器Geiger定位结果，表4为基于全相位相位差的Geiger优化迭代算法的定位结果。

图1 断铅实验8个传感器接收到的信号及其小波分解信号

表2 8个传感器接收到的信号及小波分解后子带信号主频 单位：kHz

表3 美国生产PCI-2型声发射仪器Geiger定位结果

表4 基于全相位相位差法的Geiger定位结果

图2为4种方法定位结果平均绝对误差比较。

图2 4种方法定位结果平均绝对误差比较

通过比较，基于全相位相位差的Geiger优化迭代算法的定位结果相比美国PCI-2型声发射仪器的定位结果的平均误差降低了约5 mm；相比全相位相位差法声发射定位结果，平均误差降低了约2 mm；相比美国PCI-2型声发射仪器Geiger定位结果，平均误差降低了约2 mm。

3 结论

①在小波分解基础上，全相位频谱分析与相位差法结合进行AE信号时间差估计，有效地减小了误差。

②与单独使用最小二乘法确定初始迭代试验点相比，全相位相位差法能够更快进入收敛范围，避免了对传感器坐标位置选取严格的缺点。

③全相位相位差法的Geiger优化迭代定位算法定位精度比美国PCI-2型声发射仪器的定位结果精度明显提高了。从图1中发现，在定位实验点最后两位的效果不如前几个点效果，出现原因为Geiger定位对初始迭代值要求严格，所以结果好坏很大程度由全相位求初始值决定，所以第一步是关键，初始值选择需进一步优化，信号分析能力需进一步提高。特别指出各试验点相互独立，所以个别点不代表整体效果。因为每个试验点的传感器接收的信号不同，所以每个点的的初始迭代值是不同的，为了避免出现不理想的情况，在小波分解细节信号层数时需要选出效果最好的一层，所以为了得到好的效果，需要尽可能多的层数分解，通过一个点的实验比较，找出效果最好的一层，再往下进行别的点的定位实验，以达到最优定位效果。

④基于全相位相位差的Geiger优化迭代定位新算法为岩石声发射定位研究提供了一种途径。

［1］Mogi K.Study on Elastic Shocks Caused by the Fracture of Hetero⁃geneous Material and Its Relation to Earthquake Phenomena［J］.Bull of the Earthquake Research Institute，1962，40（6）：831-853.

［2］Scholz C.Experimental Study of the Fracturing Process in Brittle Rock［J］.Journal of Geophysical Research，1968，73（5）：1447-1454.

［3］胡新亮，马胜利，高景春，等.相对定位方法在非完整岩体声发射定位中的应用［J］.岩石力学与工程学报，2004，23（2）：277-283.

［4］赵兴东，刘建坡，李元辉，等.岩石声发射定位技术及其实验验证［J］.岩土工程学报，2008，30（10）：1472-1476.

［5］康玉梅，刘建坡，李海滨，等.一类基于最小二乘法的声发射源组合定位算法［J］.东北大学学报，2010，31（11）：1648-1651.

［6］张会新，陈德沅，彭晴晴，等.一种改进的TDOA无线传感器网络节点定位算法［J］.传感技术学报，2015，28（3）：412-415.

［7］杨文铂，邢鹏康，刘彦华.一种基于自适应RSSI测距模型的无线传感器网络定位方法［J］.传感技术学报，2015，28（1）：137-141.

［8］黄晓红，张艳博，田宝柱，等.基于相位差时延估计法的岩石声发射源定位研究［J］.岩土力学学报，2015，36（2）：382-383.

［9］卢新宁.基于全相位FFT的铁道信号频率检测算法研究［D］.海南：海南大学，2013.

［10］庞前娟，孙山林，魏丽娜.基于全相位FFT的故障信号检测方法［J］.制造业自动化，2010，32（7）：96-99.

［11］马学敏.岩石声发射信号定位研究［D］.河北：河北联合大学，2014.

［12］马荣田.岩体声波测试技术及其在巷道围岩岩体波速测试中的应用［J］.铁道建筑，2006，10：37-40.

［13］刘建坡，王洪勇，杨宇江，等.不同岩石声发射定位算法及其实验研究［J］.东北大学学报，2009，30（8）：1194-1195.

［14］黄晓红，邓振淼.改进的相位展开算法及其在瞬时频率估计中的应用［J］.电子学报，2009，37（10）：224-230.

黄晓红（1973-），女，汉族，河北省唐山人，教授，博士，华北理工大学信息工程学院硕士生导师，主要从事信号与信息处理方面的教学和研究工作，tshxh@163.com；

孙国庆（1988-），男，汉族，河北省张家口人，华北理工大学电气工程学院硕士，主要从事信号与信息处理方面研究工作，457297857@qq.com。

张凯月（1992-），女，汉族，河北省沧州人，华北理工大学信息工程学院硕士，主要从事信号与信息处理方面研究工作，10322872757@qq.com。

Rock Acoustic Emission Source Localization Method Based on All Phase and Geiger Algorithm*

HUANG Xiaohong1*，SUN Guoqing2，ZHANG Kaiyue1
（1.College of information engineering，North China University of science and technology，Tangshan Hebei 063009，China；2.College of electrical engineering，North China University of science and technology，Tangshan Hebei 063009，China）

Geiger localization algorithm is widely used in the analysis of rock localization，however，it is very strict on the initial value，if the initial value is not properly selected，it is difficult to enter the convergence range.In order to improve the positioning precision and reduce the number of iterations，rock acoustic emission source localization method based on all phase and Geiger algorithm is put forward.First of all，the experiment was carried out on the granite（50 mm×100 mm×50 mm）.Secondly，making full use of the advantage of apfft phase invariance to analyse the lead signal，and the delay time is obtained by the phase difference method，at the same time，the initial value of the Geiger iteration is obtained by the inversion of the acoustic emission source.In the end，combining least square method and Geiger algorithm to obtain optimum solution.Experimental simulation results are shown：Comparing the positioning results of the United States PCI-2 type acoustic emission instrument，the average error decreased by about 5 mm.This method can effectively solve the problem of selecting the initial value of Geiger，so that it can quickly enter the convergence range，improving the convergence speed and positioning accuracy.

signal analysis；acoustic emission source location；all-phase phase difference；Geiger；least square method EEACC：7230；7310N

10.3969/j.issn.1004-1699.2016.11.013

TU45

A

1004-1699（2016）11-1705-06

项目来源：国家自然科学基金面上项目（51174071；51374088）；河北省钢铁联合基金项目（E2016209357）；华北理工大学培育基金项目（GP201506）

2016-05-14 修改日期：2016-06-27