三角测距激光雷达的光斑定位算法研究*

李 高，何元烈，曾 碧

（广东工业大学计算机学院，广州510000）

三角测距激光雷达的光斑定位算法研究*

李 高，何元烈*，曾 碧

（广东工业大学计算机学院，广州510000）

为了降低激光雷达测距系统的光斑信号噪声，提高系统的测距精度，对属性距离加权平均滤波及灰度质心法进行改进，提出一种应用于激光雷达系统的改进算法。以曲率为属性的属性距离加权平均滤波在去噪的同时很好地突出了光斑的峰值点。通过多次迭代计算灰度质心的求质心方法，进一步地提高光斑中心的定位精度，还解决了一般平方加权质心法容易受到噪声影响的问题。在MATLAB仿真环境中对实际采集的数据进行处理，实验表明本文算法对于4 μs的像素单元可以取得0.05 pix的定位精度，并具有较好的稳定性。

机器人传感器；二维激光雷达；亚像素定位；属性距离加权平均滤波；平方加权质心法

激光雷达LIDAR（Laser Radar）［1］是基于激光的距离测量系统，包括单点的测距传感器、在平面上进行线扫描的二维激光雷达［2］、在空间上进行面扫描的三维激光雷达［3］。作为移动机器人的关键组成部分之一，激光雷达在移动机器人中的应用主要有3个方面，即障碍物检测、路标检测及地图匹配、探索行驶时建立地形图。由于激光雷达能快速提供环境的信息，移动机器人的发展在很大程度上得益于激光雷达的研发。尽管激光雷达的研制已进行多年并逐步实现了商业化，并在一些领域得到了应用，但仍有许多方面需要改进的。

目前，很多机器人都采用三维激光雷达［4］，而且也取得了较好的效果，但是三维激光雷达价格昂贵，体积大而笨重，尤其是成像速度慢的弱点，在很大程度上制约了它的进一步应用。同三维激光雷达相比，二维激光雷达具有测距速度快、系统稳定可靠的特点。所以二维激光雷达室内的移动机器人应用中有明显的优势，因为在室内的结构化环境下，地面平坦，所有障碍物又都几乎与地面垂直，利用二维激光雷达机器人能更迅速地在平行地面上获取环境导航信息。

国内对于激光雷达的研究相对较少，导致国内许多关于机器人自主导航算法的研究不得不依赖国外的进口传感器。当前较为成熟的二维激光雷达产品有日本HOKUYO所生产的PBS-03JN、UAM-05LP-T301等，然而这些产品普遍采用的是相位式的测距方式，硬件成本都比较昂贵。本文所述的激光雷达系统基于激光三角测距原理，研究了在快速旋转运动情况的激光光斑的稳定性，受噪声影响的问题，及光斑亚像素的定位算法。使二维激光雷达系统达到了3 m量程和1 mm的精度应用需求条件下，在设计成本方面仍然可以得到控制。

激光三角测距系统［5］即激光光源、被测物面、光接收系统三点共同构成一个三角形光路，由激光器发出的光线，经过汇聚透镜聚焦后入射到被测物体表面上，光接收系统接收来自入射点处的散射光，并将其成像在光电位置探测器敏感面上，通过光点在成像面上的位移来测量被测物面移动距离的一种测量方法。单点式激光三角法测量可分为直射式和斜射式两种结构［6-7］，本文采用斜射式激光三角测距法，原理如图1所示。激光器发射的平行光线，经过会聚透镜聚焦后形成一束光，该光束垂直射到被测物体表面。待测目标面的相对移动或其表面变化都会导致入射光点沿入射光轴前后移动。测量激光的散射光经接收透镜垂直照射到光电位置探测器上，如果入射光点在光电探测器形成了位移x，则待测目标面沿轴方向的相对位移为d。依据三角测距法的位置关系我们可根据下式计算出d的值：

式中，s为入射光点与接收透镜入光点的距离，f为接收透镜入光点到成像面的垂直距离，β为入射激光光轴与接收透镜光轴的夹角。

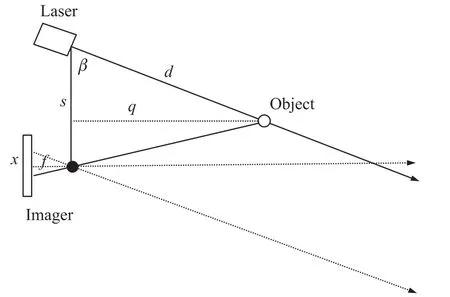
图1 三角测距原理

1 噪声及去噪分析

激光三角测距算法测距中的准确性很大程度依赖于激光光斑定位的精确性［8］，在实际应用中光斑的定位经常会受到噪声的影响导致定位产生较大的误差，这种误差主要受两方面的噪声产生［9］，一是由像元的读出噪声、暗电流散粒噪声、光子散粒噪声、固定模式噪声和光谱响应不均匀性等造成的随机噪声［10-11］，另一方面是由图像传感器有限空间采样宽度带来的灰度平均效应以及像元填充率、填充形式带来的系统噪声。图2为激光雷达系统在受噪声影响下所收集的光斑信号，本文依据属性距离加权平均滤波的原理对这种不可避免的随机噪声及系统噪声加以处理。

图2 受噪声的激光光斑

属性距离加权平均滤波ADWA（Attribute Distance Weighted Average）［12］由基本加权滑动平均滤波改进而来，以不同的距离属性作为信号的权值。对一维信号的处理，属性距离加权平均滤波表示为：

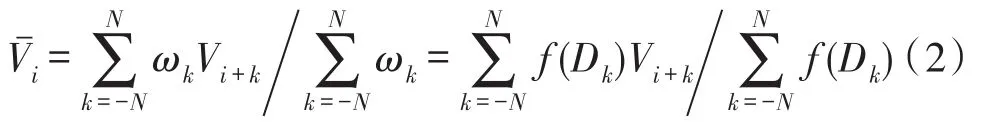
式中，Vi+k为采样信号值，为对应于Vi的滤波结果，ωk=f(Dk)为采样点Vi+k的权系数，Dk为多元属性距离。记第i个采样点的第m个属性为Ami，则第（i+k）采样点和第i采样点之间的M元属性距离表示为：

式中，dm为属性基距离，σm为属性Am的正规化系数，用于调节相应属性在滤波过程中的作用力度。

属性距离反映了采样数据点之间在多个属性上的差异，实质上也反映了信号和噪声之间的差异。因此ADWA是从多属性角度来分离噪声和信号，克服了其他滤波方法只局限于信号个别属性的缺点。本文以位置、幅度、曲率作为属性距离公式的三个元素，曲率反映了曲线在某一点上的弯曲程度，在图像信号及计算机视觉等领域都有较重要的应用，能在去噪的同时很好地突出光斑的峰值点。则属性距离计算公式表示为：

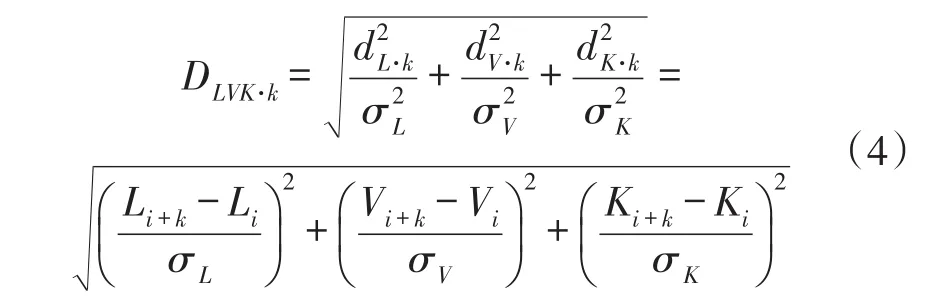
式中，L、V、K分别为位置、幅度、曲率值，σL、σV、σK分别为位置、幅度、曲率系数，可以通过这3个参数调整位置、幅度、曲率属性的影响权重，本文将其统一设置为1。

以Rosenfeld等提出的k余弦曲率计算方法对光斑离散曲线的曲率进行估计［13］，对于给定的参数k，k余弦曲率首先在曲线当前点pi处定义2个矢量：

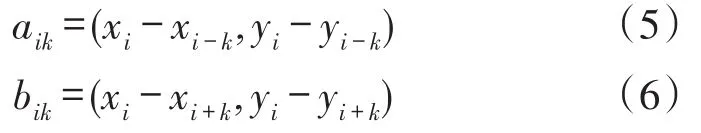
式（5）、（6）中(xi,yi)、(xi-k,yi-k)、(xi+k,yi+k)都是曲线上的坐标点，通过式（7）计算aik和bik夹角的余弦值cik：

为了选取合适的参数k，首先确定k的最大值，记为m，然后取 k=m,m-1,m-2,…，计算 cim，ci,m-1，…，根据条件 cim＜ci,m-1＜…＜cik≥ci,k-1对k值进行选取，cik即作为当前点pi的离散曲率值。

2 光斑定位算法

理想的光学系统能使平行光束聚焦成像在CCD上的一个像素上，如图3所示。而实际测量中，由于光学系统的成像误差、衍射、散射以及CCD器件本身的噪声影响，会使所成的像变成一个光强按某种分布占据多个像素的光斑，其光斑信号如图4所示。对于这种光斑信号模型，可以通过算法求出其质心，并以此质心作为光斑中心的准确位置，可以将光斑的定位提高到亚像素级别，从而提高了CCD分辨率。

图3 理想光斑

图4 实际光斑

假设成像在CCD的光敏面上的光斑覆盖光敏面像元个数为m。由于其像素输出信号的模型近似为高斯分布，所以可以用灰度质心法来求光斑中心，经典灰度质心法［14］可以由式（8）给出：

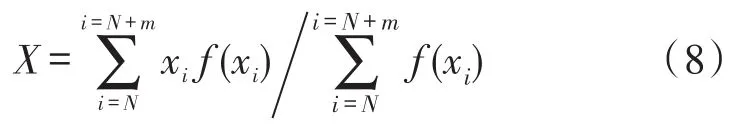
经典的灰度质心法很容易受到噪声的影响，在有噪声的情况下亚像素的定位精度将会严重下降，即使在无噪声影响的情况下的定位精度也只能达到0.1 pix。为了进一步解决亚像素的精确定位问题，本文通过线性插值的平方加权及多次迭代的方法对灰度质心法进行优化，线性插值平方加权后的公式可以由式（9）表示：

式（8）、式（9）中，X为光斑灰度质心的位置，N为光斑正态分布的起始像素坐标，则N+m为结束坐标，xi为第N+i个像素位置，f(xi)为第N+i个像素位置上的灰度值大小。

f(xu)为线性插值点u上的灰度值，根据线性插值理论得到 f(xu)的计算公式如下：

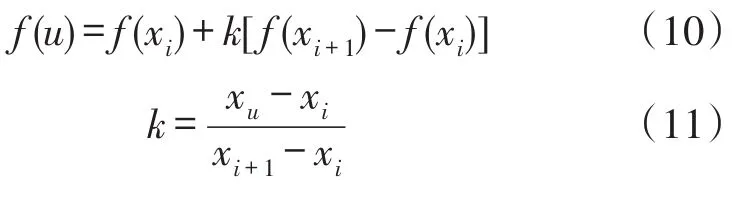
式（10）、式（11）中k为斜率，(x,f(x))为曲线上的坐标点。

基于线性插值的平方加权质心法通过线性插值弥补了物理像素点有限性、离散性的缺点，提高了有效的像素点数量，用灰度值的平方作为权值，突出了离中心较近的较大灰度值像素点对中心位置的影响，对系统噪声起到了很好的去除作用。然而当传感器处于快速旋转运动的情况下，很容易造成光斑信号对称性差的问题，如图5所示，这样的问题无法通过简单地消除系统噪声的方法来获得高精度的亚像素点。为了解决这个问题，本文通过多次迭代计算灰度质心可以获得更好的定位精度及稳定性。

图5 扭曲的激光光斑

在灰度质心法的基础上根据质心估计值的偏差进行多次迭代计算，直到偏差小于一定的阈值为止。每次迭代计算前先由式（12）进行质心估计值的偏差衡量：

式中，X为当前计算的光斑中心，N为光斑正态分布的起始像素坐标，光敏面上的光斑覆盖光敏面像元个数为m，所以上一次的光斑估计值为，通过当前光斑中心的计算值与光斑估计值的差值计算偏差衡量因素σ。如果|σ|大于设定的阈值，则调整正态分布的起始像素为N+σ，用灰度质心法公式重新估计光斑质心。如此迭代，直至|σ|满足阈值要求。

如图6为本算法的具体流程图，通过设置阈值寻找光斑的位置，从而确定光斑在像元的覆盖范围m，这个阈值的设定有多种方式，可以是最大值法、均值法等，由于这个光斑位置并非是准确的实际光斑位置，所以在迭代算法中通过重复确定质心，在像元覆盖个数m确定的情况下调整光斑的位置，通过以上方式可以在初始及迭代过程中确定光斑的正态分布范围。多次迭代计算灰度质心的求质心方法，不但使光斑中心的定位精度达到了0.05 pix左右，还解决了一般平方加权质心法受噪声影响大的问题，即使光斑信号出现对称性差的情况下，依然能较好地获得光斑中心的定位。

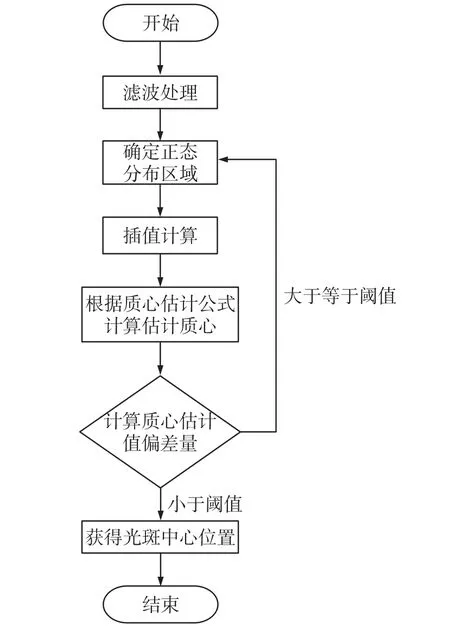
图6 算法流程

3 实验

本文所述的激光雷达系统，以DLSI-2K作为线性感光元件，DLIS-2K线阵图像传感器灵敏度可达160 V/lux-s，包括4行像素，每行有2 081个光学像素和16黑像素。其中3行为4×4 micron方形像素，另一行为4×32 micron长方形像素。以STM32F103C8T6作为核心处理单元，速度可达72 MHz，具有64 kbyte的程序存储容量。激光雷达系统结构如图7所示，测距系统位于一个可连续旋转的平台之上，由电机带动旋转平台进行快速旋转，使测距系统可以对整个水平面进行测距。

图7 激光雷达系统

由于激光雷达系统工作在一个快速旋转的状态中，光斑信号很容易受到各种噪声的影响，甚至产生变形，不能通过简单的高斯模型进行模拟，所以本文的实验将采用实际的光斑数据进行实验。为了获得激光雷达系统的光斑信号数据，将系统固定于水平移动平台之上，只对角度为0°的数据进行输出，调整激光雷达系统所处的水平位置来获得不同距离的光斑信号数据。为了直观的反映算法的性能，本文首先在PC端通过串口收集激光雷达获取的光斑信号，然后再用MATLAB对数据进行处理。

3.1 亚像素点的精度对比实验

为了获取较为理想的光斑估计中心，本文用平均滤波处理后采用灰度质心法计算光斑中心，取50次平均值作为光斑中心的估计值［15］。实验分别对400 mm、450 mm、500 mm、550 mm、600 mm、650 mm、700 mm、750 mm、800 mm、850 mm、900 mm处获取的光斑信号进行处理，每个距离都取10组不同的数据进行计算，取误差值的绝对值计算平均值作为光斑中心的测量平均误差。

图8为使用平均滤波、中值滤波及本文所述的ADWA滤波进行滤波处理，并用灰度质心法获取的光斑中心误差值对比。图9为用平均滤波处理后，分别用灰度质心法、线性插值灰度质心法及本文算法获取的光斑中心误差值对比。

图8 滤波算法对比

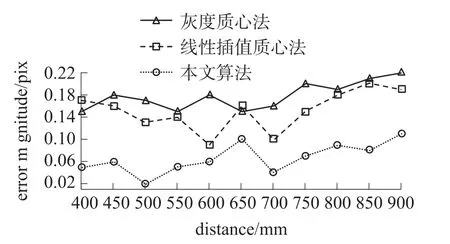
图9 亚像素定位算法精度对比

通过图8、图9的对比结果可知，本文所述的ADWA滤波对处于快速旋转的激光雷达的光斑信号的处理明显好于平均滤波及中值滤波，使光斑定位计算值依然可以达到0.1 pix的精度要求。同样，对于本文的亚像素定位算法，处理后的光斑信号误差基本在0.05 pix左右，明显优于普通质心法及线性插值的质心法。由于三角测距方式本身特性，各算法随着距离的增加误差也会不同程度增大，从整体数据来分析，ADWA滤波及本文所提的迭代质心法依然有较明显的优势。

3.2 稳定性对比实验

以500 mm的距离处获得的光斑信号对算法的稳定性进行实验，在500 mm处光斑中心的估计值为612.12 pix，通过本文所述的ADWA滤波算法处理后，分别用灰度质心法、线性插值灰度质心法及本文算法计算的光斑中心计算值。如表1所示，取10组不同的数据分别用不同的定位算法计算光斑中心计算值，取误差值的绝对值计算平均值作为光斑中心的测量平均误差，并计算光斑中心计算值标准差以反映算法的稳定性。

表1 亚像素定位算法稳定性对比

通过表1的对比可以发现，在测量误差方面，质心法，线性插值质心法和本文算法的测量平均误差逐渐减小，本文算法相对与传统的质心法有3倍以上的提高，相对与改进的线性插值质心法也有1倍以上的提高。在稳定性方面，从标准差的结果可以得出，本文算法为0.053，相对与传统质心法提升了320%，而相对于线性插值质心法也有180%的提升。

本文的亚像素定位算法不管在定位误差方面还稳定性方面都是比普通质心法及线性插值法要好。

3.3 滤波效果对比实验

分别通过5×1的中值滤波、均值滤波、ADWA滤波对图2中的光斑信号进行处理，处理结果如图10所示。

图10 滤波效果对比

图10中，3种滤波都在一定程度上降低的信号的噪声，但中值滤波对于光斑峰值处噪声的处理明显是不足的，均值滤波虽然能较好地处理了峰值处的噪声，但处理后光斑的峰值明显小于原始信号峰值，而ADWA滤波可以在较好地保留了峰值特征的情况下起到去噪的作用。以均方根误差作为去噪效果的评估标准，ADWA滤波的去噪效果约为传统方式的0.5倍。

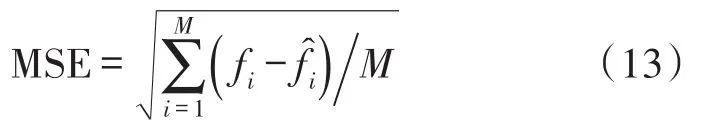
4 结论

本文主要是针对激光雷达系统所获取的激光光斑信号进行滤波算法及亚像素定位算法的研究，对于这种在快速旋转的状态中获取的激光光斑信号进行了噪声分析，并提出了相应的滤波进行去噪，并用改进的灰度质心法对亚像素进行计算。通过实验的对比，证明本文所述算法具有很好的效果，对于只有4 μs的像素单元仍能取得0.05 pix的定位精度，并在稳定性上明显优于其他算法，满足了激光雷达用于室内机器人环境感知的设计要求。

［1］Zhang J，Mao X.Optimal Bandwidth Design of Laser Radar Re⁃ceiver［C］//Optical Communications and Networks（ICOCN），2015 14th International Conference on.IEEE，2015.

［2］Fong E H L，Adams W，Crabbe F L，et al.Representing a 3-D En⁃vironment with a 21/2-D Map Structure［C］//Intelligent Robots and Systems，2003.（IROS 2003）.Proceedings.2003 IEEE/RSJ International Conference on.IEEE，2003：2986-2991.

［3］Vandapel N，Huber D F，Kapuria A，et al.Natural Terrain Classifi⁃cation Using 3-D Ladar Data［C］//IEEE International Conference on Robotics&Automation，2004：5117-5122.

［4］Brosed F J，Santolaria J，Aguilar J J，et al.Laser Triangulation Sen⁃sor and Six Axes Anthropomorphic Robot Manipulator Modelling for the Measurement of Complex Geometry Products［J］.Robotics and Computer-Integrated Manufacturing，2012，28（6）：660-671.

［5］Herrmann M，Otesteanu M，Otto M A.A Method to Determine the Extrinsic Parameter of Laser Triangulation Sensors，With Restrict⁃ed Mobility［C］//Electronics and Telecommunications（ISETC），2014 11th International Symposium on.IEEE，2014.

［6］Breier M，Moller P，Li W，et al.Accurate laser Triangulation Us⁃ing a Perpendicular Camera Setup to Assess the Height Profile of PCBs［C］//Industrial Technology（ICIT），2015 IEEE International Conference on.IEEE，2015：1613-1618.

［7］Ferreira Barreto S V，Eskinazi Sant’Anna R，Feitosa M A F.A Method for Image Processing and Distance Measuring Based on Laser Distance Triangulation［C］//Electronics，Circuits，and Sys⁃tems（ICECS），2013 IEEE 20th International Conference on.IEEE，2013：695-698.

［8］Lefebvre D，Doucet M，Duval Y，et al.3D Laser Triangulation Compensation for Non-Uniform Surfaces Reflectivity［C］//Applied Industrial Optics：Spectroscopy，Imaging and Metrology.Optical Society of America，2013.

［9］马玉良，许明珍，佘青山，等.基于自适应阈值的脑电信号去噪方法［J］.传感技术学报，2014，27（10）：1368-1372.

［10］纪峰，李翠，常霞，等.基于改进阈值函数的自适应图像去噪方法［J］.传感技术学报，2014，27（3）：351-354.

［11］张辉，袁家虎，刘恩海.CCD噪声对星敏感器星点定位精度的影响［J］.红外与激光工程，2006，35（5）：629-633.

［12］熊刚，丁天怀，王鹏.应用属性距离加权平均滤波提高CCD光斑的亚像素定位精度［J］.光学精密工程，2012，20（5）：1102-1109.

［13］郭娟娟，钟宝江.U弦长曲率：一种离散曲率计算方法［J］.模式识别与人工智能，2014（8）：683-691.

［14］陈晓东，李为民.利用重心法求光斑信号位置的误差分析［J］.光学技术，2000（1）：5-608.

［15］陈运锦，冯莹，魏立安，等.光斑质心亚像素定位误差的实验研究［J］.光电工程，2010，37（2）：80-84.

李 高（1992-），男，硕士研究生，主要研究方向为机器人传感器、机器人，lg16@qq.com；

何元烈（1976-），男，工学博士，广东工业大学计算机学院副教授，硕士研究生导师，研究方向为计算机视觉、机器人、物联网等，heyuanlie@163.com；

曾 碧（1963-），女，工学博士，广东工业大学计算机学院教授，主要研究方向为智能信息处理、智能机器人等。

Spot Positioning Algorithm for Laser Radar Based on Triangulation*

LI Gao，HE Yuanlie*，ZENG Bi
（School of Computer Science Guangdong University of Technology，Guangzhou 510000，China）

In order to reduce the noise of light spot of laser radar system and improve the precision of the distance measurement for the system，an advanced algorithm based on attribute distance weighted average filter algorithm and gray-gravity method algorithm was proposed.The attribute distance weighted average filter with the property of curvature can not only reduce the noise of light spot，but also can highlight the peak spot of the laser facula.While the method by using iterative calculations for gray centroids would further improve the positioning accuracy of light spot and it can also solve the problem of susceptible to noise by using the square weighted gray-gravity method.Ex⁃periments have dealt with the collected practical data in MATLAB simulation environment，and the results of the ex⁃periments show that the algorithm can achieve positioning accuracy with even 0.05 pix for 4 μs pixel unit.Many re⁃peated experiments indicated that the experimental results had a good stability.

robot sensor；2-D laser radar；sub pixel positioning；attribute distance weighted average filter；square weighted gray-gravity method algorithm

TP212.6

A

1004-1699（2016）11-1692-06

EEACC：6320；4360B 10.3969/j.issn.1004-1699.2016.11.011

项目来源：广东省产学研合作专项资金项目（2014B090904080）；广东省应用型科技研发专项资金项目（2015B090922012）；东莞市产学研合作项目（2015509109107）

2016-03-17 修改日期：2016-07-05