骨折非平衡牵引与骨折移位关系数学模型的初建与应用

叶丹丹，张 飞，陈 伟，郑占乐，李 升，张英泽(河北医科大学第三医院创伤急救中心，河北省骨科研究所，河北省骨科生物力学重点实验室，河北 石家庄 050051)



·研究快报·

骨折非平衡牵引与骨折移位关系数学模型的初建与应用

叶丹丹，张 飞，陈 伟，郑占乐，李 升，张英泽*(河北医科大学第三医院创伤急救中心，河北省骨科研究所，河北省骨科生物力学重点实验室，河北 石家庄 050051)

骨折；牵引术；数学模型

牵引是临床常用的骨折复位方法[1-3]。骨折远端牵引针的角度、方向与骨折复位，包括旋转移位、重叠移位、侧方移位，有着直接关系。牵引针的方向会影响到肢体机械轴线和骨折周围软组织的运行轨迹，若牵引针的角度不正常，则移位的骨折端难以达到正确的复位。本研究通过生物力学实验并建立数学模型来观察远端牵引针角度与骨折远端的移位关系。

1 理论基础

刚体变换是指一个刚性几何体在三维空间中作旋转、平移的运动。 在运动学里，刚体在作一个位移的时候，刚体内部至少有一点固定不动，则此位移等价于一个绕着包含那固定点的固定轴的旋转。三维平移变换、比例变换可看成是二维情况的直接推广。但旋转变换则不然，因为我们可选取空间任意方向作旋转轴，因此三维变换处理起来更为复杂。若以坐标系的三个坐标轴x、y、z分别作为旋转轴，则点实际上只在垂直坐标轴的平面上作二维旋转。此时用二维旋转公式就可以直接推出三维旋转变换矩阵。规定在右手坐标系中，物体旋转的正方向是右手螺旋方向，即从该轴正半轴向原点看是逆时针方向。

①绕z轴正向旋转γ角，旋转后点的z坐标值不变,x、y坐标的变化相当于在xoy平面内作正γ角旋转。

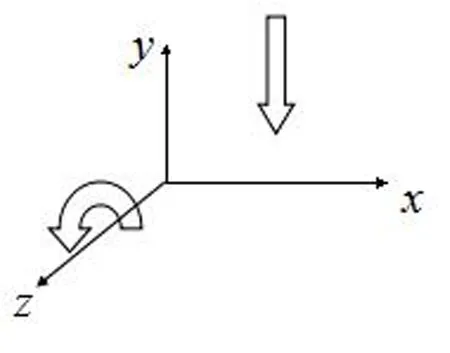
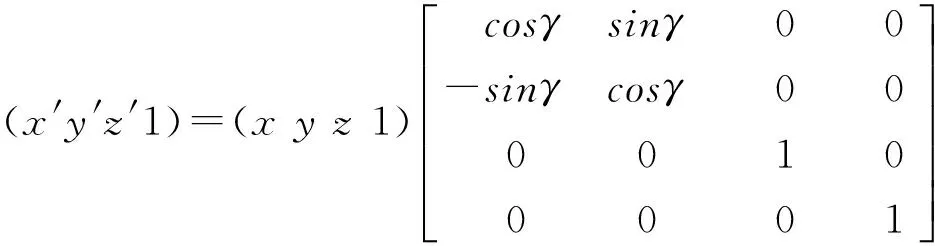
②绕x轴正向旋转α角，旋转后点的x坐标值不变，y、z坐标的变化相当于在yoz平面内作正α角旋转。

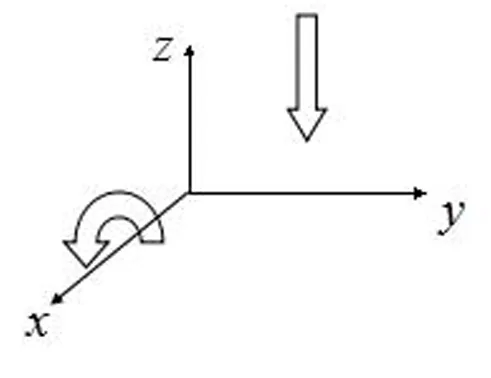
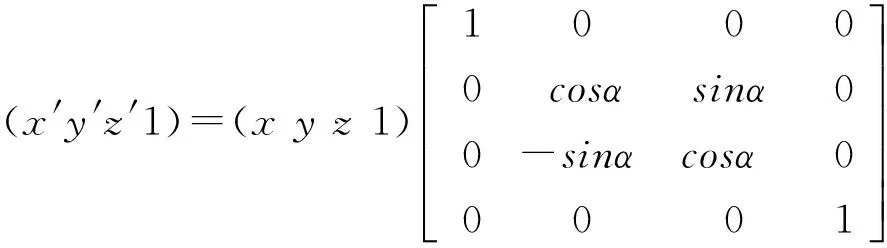
③绕y轴正向旋转β角，y坐标值不变，z、x的坐标相当于在zox平面内作正β角旋转。

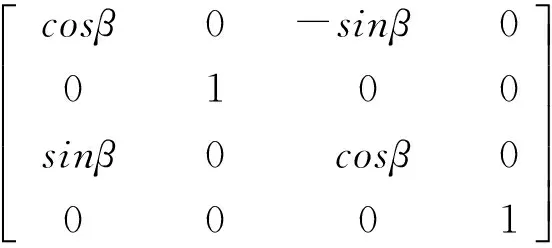
2 数学模型

2.1 模型1 以股骨干骨折为例进行建模，把股骨理想化为一个圆柱体，每次牵引针均经过圆柱的轴，不考虑肌肉对最终牵引效果的影响。在这个模型里，骨折近端的矢状面是一个平面α，牵引针是看作线段AB，作经过骨折远端圆柱的轴且与平面α垂直的平面β。任取在骨折远端圆柱的轴上一点O为空间直角坐标系的原点，以此圆柱的轴为x轴，在平面β过点O作垂直于x轴的直线为y轴，过点O作垂直于平面β的直线为z轴。点O1是骨折远端的切平面的圆心(图1)。

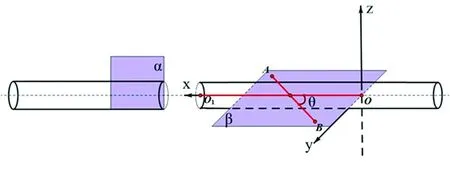
图1 立体模型1的空间直角坐标系

证明：设骨折远端圆柱的轴OO1与牵引针AB的夹角为。在平面β上的牵引针AB在牵引力的作用下，绕z轴负向旋转，这样使在平面β上的牵引针AB与y轴平行。因为牵引针AB在冠状面β上旋转，所以骨折远端圆柱自身不会发生转动。我们可以把骨折远端圆柱看作为线段OO1。设点O1的坐标为(x0,0,0)，旋转后点O1的坐标为(x′,y′,z′)，则：

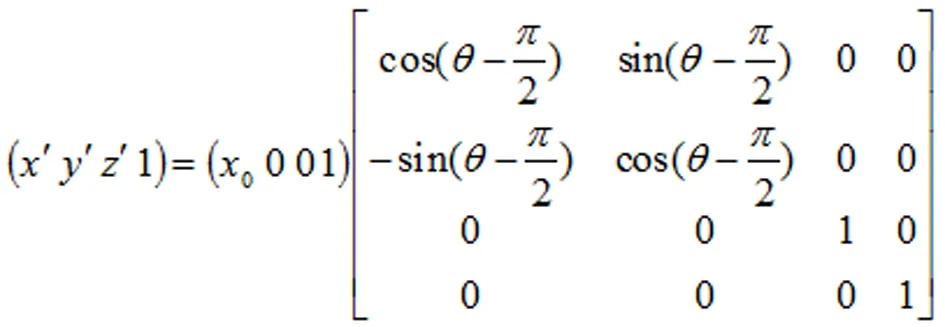
此时，牵引针AB与线段OO1在平面xoy上，所以我们可以转换到二维空间上计算(图2)。

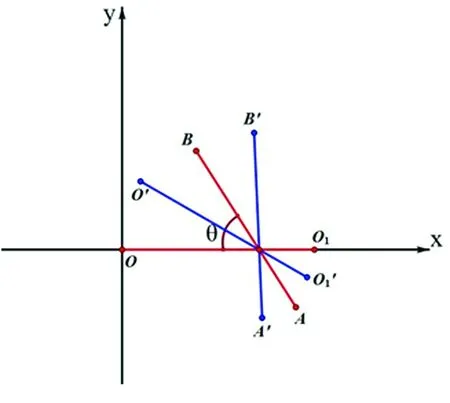
图2 牵引针在冠状面上旋转变化的平面直角坐标系

在图2中，点O1的坐标为(x0,0)，旋转后点O1的坐标为(x′,y′)，则：

即x′=cos((。直线OO1与直线的夹角为。

2.2 模型2 在模型1的基础上，作垂直于骨折远端圆柱的轴的平面γ，O是骨折远端圆柱的轴与平面γ的垂足，牵引针是看作在平面γ上的过点O的线段AB。以O为空间直角坐标系的原点，以此圆柱的轴为x轴，在平面γ上，过点O作垂直于x轴的直线为y轴，过点O作垂直于y轴的直线为z轴。点O1是骨折远端的切平面的圆心，线段EF是一个在y轴上的线段(图3)。

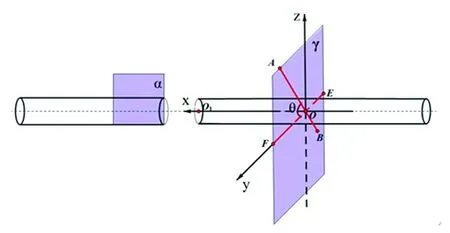
图3 立体模型2的空间直角坐标系

证明：设在水平面上的y轴与牵引针AB的夹角为。在平面γ上的牵引针AB在牵引力的作用下，绕x轴负向旋转，这样使在平面γ上的牵引针AB与y轴重合。因为牵引针AB在平面γ上旋转，所以骨折远端圆柱自身发生转动，整体不会发生移动。此时，牵引针AB与骨折远端圆柱自身在平面yoz上，所以我们可以转换到二维空间上计算(图4)。

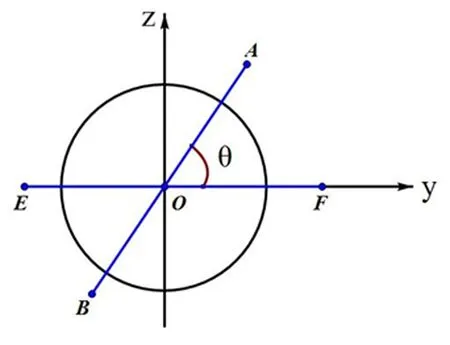
图4 牵引针在水平面上旋转变化的平面直角坐标系

此时，若是牵引针AB与y轴重合，则牵引针AB需要旋转角，即是股骨没有发生位移的变化，只是自身发生了旋转，使骨折处的吻合度发生变化。

3 讨 论

牵引是纠正骨折移位最常用的方法。但如果牵引针的角度和方向与肢体的机械轴线不一致，违背了肌肉的正常运行轨迹，牵引会使骨折端发生旋转、成角或侧方移位等[4]。许多骨科医生在临床实践中已经认识到了平衡牵引的重要性。目前，平衡的改变与骨折端移位的关系，特别是生物力学性能、肌肉的运行轨迹与骨折远端的移位关系尚未建立数学模型。本研究通过对新鲜整具尸体标本进行生物力学实验，初步建立了数学模型。

以股骨骨折为例建立数学模型，该模型将股骨理想化为一根直径均一的圆柱体，牵引针经过该圆柱的轴，不考虑肌肉及重力的影响。通过系统计算发现，若牵引针AB在冠状面与股骨成角，则牵开后远端骨折块在冠状面上最终发生的旋转。若牵引针在水平面上与冠状面成角，则牵开后远端骨折块在水平面上最终将发生角旋转。

[1] 王娟,李升,臧砚超,等.应用四肢长骨骨折快速复位器治疗股骨骨折[J].河北医科大学学报,2014,35(2):220-221，封三.

[2] 杨宗酉,陈伟,刘勃,等.应用四肢长骨骨折髓内复位器治疗股骨干骨折[J].河北医科大学学报,2014,35(11):1339-1340，封三.

[3] 魏俊强,刘利蕊,潘进社,等.仰卧位与侧卧位闭合复位髓内钉内固定治疗股骨干骨折的疗效比较[J].中华创伤骨科杂志,2013,15(8):660-665.

[4] Chen W,Zhang T,Wang J,et al. Minimally invasive treatment of displaced femoral shaft fractures with a rapid reductor and intramedullary nail fixation[J]. Int Orthop,2016,40(1):167-172.

(本文编辑：刘斯静)

2016-10-24；

2016-11-14

叶丹丹(1989-)，女，江苏宿迁人，河北医科大学第三医院实习研究员，理学硕士，从事骨科相关数学模型研究。

*通讯作者。E-mail：yzling_liu@163.com

R683

B

1007-3205(2016)11-1356-03

10.3969/j.issn.1007-3205.2016.11.032