关于高斯牛顿法的注记*

赵淑波,李立伟

(哈尔滨师范大学)



关于高斯牛顿法的注记*

赵淑波,李立伟

(哈尔滨师范大学)

用牛顿法解最小二乘问题的主要困难是Hesse矩阵和二阶项的计算.文中研究可用已求得的一阶项代替二阶项的牛顿法.为此引入一个降阶条件，并讨论此条件下的牛顿法的性质,证明了此算法在适当条件下的收敛速度是二阶的，进而还能是超线性的.

高斯牛顿法; 收敛性

1 预备知识

该文研究如下的非线性最小二乘问题：

(1)

其中r:Rn→Rm是非线性函数. 解此问题的牛顿法即是将目标函数(1)的二次Taylor展式极小化.

设J(x)是r(x)的Jacobi矩阵，

f(x)的Hesse矩阵为G(x)=J(x)TJ(x)+S(X)

其中

(2)

因此，目标函数f(x)的二次模型为

xk)IT(J(xk)TJ(xk)+S(xk))(x-xk)

(3)

从此，解问题(1)的牛顿法为

xk+1=xk-(J(xk)TJ(xk)+S(xk))-1J(xk)r(xk)

(4)

忽略S(x)以简化计算，获得有效的算法. 由(3)可知，当ri(x)接近于零或者ri(x)接近线性函数,s(x)可以忽略.

Gauss-Newton法即是在(3)中忽略G(x)s中的二阶项S(x). 从而(4)成为

xk+1=xk-(J(xk)TJ(xk))-1J(xk)r(xk)=xk+sk

(5)

这里

sk=-(J(xk)TJ(xk))-1J(xk)r(xk). 因此，Gauss-Newton法的第k次迭代为

(a)解J(xk)TJ(xk)s=-J(xk)r(xk)得sk;

(b)令xk+1=xk+sk.

从迭代(5)，Gauss-Newton 法仅需r(x)的一阶导数信息. 于是，Gauss-Newton法的性质取决于G(x)中舍弃的二阶项S(x)在G(x)中是否重要. 下面定理表明，若S(x*)=0, 则Gauss-Newton法(5)具二阶收敛速度；若相对J(x*)TJ(x*)来说，S(x*)更小，则(5)是局部Q线性收敛的.

定理1.1 设f∈C2,x*为问题(1)的局部极小值点，J(x*)TJ(xI*)是正定的.并且由迭代(5)生成的点列收敛于x*, 则当 G(x)与(J(x)TJ(x))-1在x*的邻域内Lipschitz连续时，有

‖xk+1-x*‖≤‖[J(x*)TJ(x*)]-1‖‖S(x*)‖‖xk-x*‖+O(‖xk-x*)‖2)

2 主要定理

(6)

∀x,y∈Uδ0(x*),对某个δ0,∀z∈Rn以及∀h=1,2,…m和∀i=1,2,…n；其中ki为常数.

在这个条件下，上述最小二乘问题的二次模型为：

(J(xk)Tr(xk))T(x-xk)+

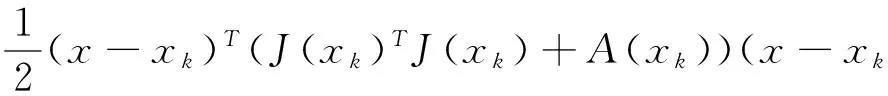
于是,在(6)条件下，牛顿法(条件降价Gauss-Newton法)为：

xk+1=xk-(J(xk)TJ(xk)+A(xk))-1J(xk)Tr(xk)=xk+sk

(7)

其中

据统计，1949年底，昆明电网发电装机总容量为9170千瓦。22千伏输电线路152.4千米，有万钟街、西站、木希村、东庄等4个变电站，小坝、小坡脚等变电塔，企业自有的桥头村钢厂、安宁钢厂、大渔村碾米厂、海源寺抽水站、明良煤矿等变电站。昆明年售电量为0.2991亿千瓦时。

sk=-(J(xk)TJ(xk)+A(xk))-1(J(xk)Tr(xk).

因此，上述条件降阶Newton法的第k次迭代为：

(a)取x0∈Uσ0(x*0(上述降阶条件中的x*的邻域)

(b)解(J(xk)TJ(xk)+A(xk))s=

-J(xk)r(xk),求得sk.

(c)令xk+1=xk+sk.

定理2.1 设f∈C2,x*为问题(1)的局部极小点,J(x*)TJ(x*)具正定性. 并且迭代(2.2)生成的点列以x*为极限.则当J(x)TJ(x)与J(x)TJ(x))-1在x*的某邻域内Lipschitz连续时，有

‖xk+1-x*‖≤M‖xk-x*‖2.

证明 由于J(x)TJ(x)与(J(x)TJ(x))-1在x*附近是Lipschitz连续的，故存在σ,α,β>0,使得对于任意两点x,y∈Uσ(x*)有

‖J(x)TJ(x)-J(y)TJ(y)‖≤α‖x-y‖,

‖(J(x)TJ(x))-1-(J(y)TJ(y))-1‖≤β‖‖x-y‖.

且由ri(i=1,2,…,n)连续,|ri(x)|≤M,∀x∈Uσ0(x*),对某个M>0.

由于f∈C2,且假设条件成立,故

g(xk+s)=g(xk)+G(xk)s+o(‖s‖2).

对范数充分小的s.

事实上，由Taylor展式，有

θ∈(0,1),i=1,2,…,n.

又从假设有

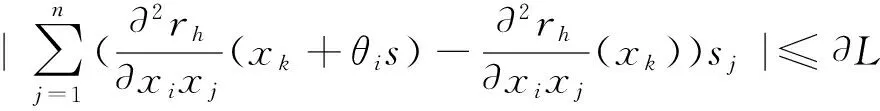
从而

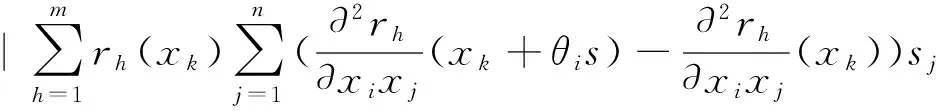
由微分中值定理，存在ηh∈(0,1)使得

上面最后一个不等式右端

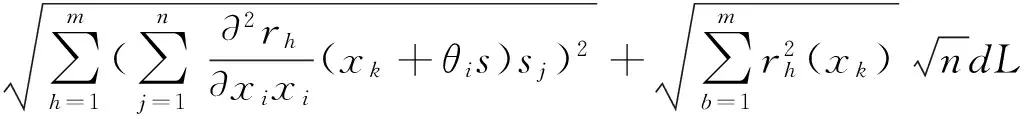
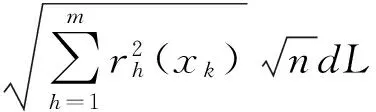
注意到,由已知，f∈C2且xk,xk+θis,xk+ηhθis∈Uσ0(x*)由

在Uσ0(x*)上有界，即存在k>0,s.t.上式最后一个不等式右端 .

类似的，我们有

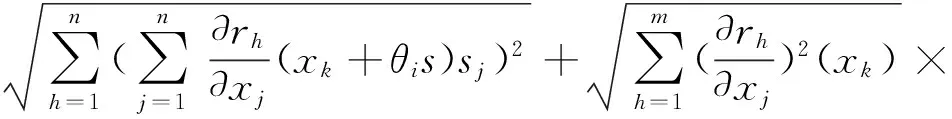
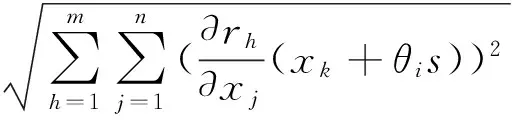
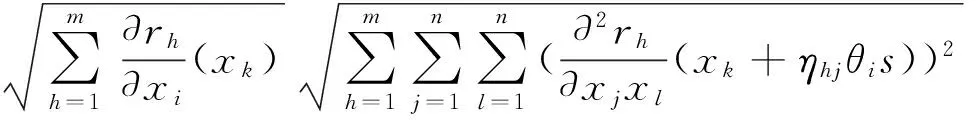
|令hk=xk-x*,有g(x*)=g(xk-hk)=g(xk)-g(xMk)hk+o(‖hk‖2).

把这两个带入上式可得

J(xk)Tr(xk)-(J(xk)ITJ(xk)+s(xk)hk)+o(‖hk‖2))=0.

由算法，以(J(xk)TJ(xk)+A(xk))-1剩以上式两边,可得

(J(xk)TJ(xk)+A(xk))-1J(xk)Tr(xk)-(J(xk)TJ(xk)+A(xk))-1(J(xk)TJ(xk)+A(xk)+s(xk)-A(xk))hk+o(‖hk‖2)=0.

即

-sk-hk-(J(xk)TJ(xk)+A(xk))-1(s(xk)-A(xk))hk+o(‖hk‖2))=0.

于是，由sk+hk=(xk+1-xk)+(xk-x*)=

xk+1-xI*,则有

‖xk+1-x*‖≤‖(J(xk)TJ(xk)+A(xk))-1‖‖(s(xk)-A(xk))(xk-x*)‖+o(‖xk-x*‖2)≤‖(J(xk)TJ(xk)+A(xkl))-1‖o(‖xk-x*‖2)+o(‖xk-x*‖2).

又由当xk在x*的邻域内对充分大的 k(J(xk)TJ(xk)+A(xk))-1上有界即

‖J(xk)TJ(xk)+A(xk))-1‖≤

2‖(J(x*)TJ(x*)+A*)-1‖

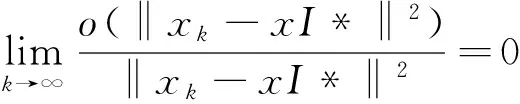
o(‖xk-x*‖2)≤M‖xk-x*‖2.对充分大的k，和某个正数M>0成立.

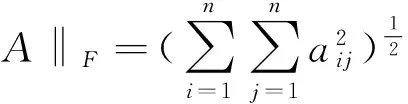
定理2.2 设f:D⊆Rn→R,f∈C2D是开凸集,设 J(X)在D上Lipschitz连续，即

‖J(x)-J(y)‖≤r‖x-‖.∀x,y∈D.

而且‖J(x)‖F≤α,∀x∈D又存在x*∈D和λ,σ>0使得J(x*)Tr(x*)=0.并假设J(x*)TJ(x*)+S(x*)正定,及在Uδ0(x*)上降阶条件(6)成立，对某个δ0.λ是J(x*)TJ(xU)+S(x*)的最小特征值，并且如下不等式成立

‖J(x)-J(x*))Tr(x*)‖≤σ‖x-x*‖.∀x∈D

(8)

如果σ+‖S(x*)‖<λ,那么对任意c>1,且c(σ+c‖S(x*)‖)<λ,存在ε>0,使得对任意x0,x1∈N(x*,ε)由(3.12)产生的序列有定义，并且收敛到x*,同时满足

证明 用归纳法.由已知，假设λ>σ+‖S(x*)‖>0且c>1c(σ+c)‖S(x*)‖<λ,是一个常数,由于J(x*)TJ(x*)+G(x*)正定，存在 ,使得x0,x∈Uε′(x*)时，有

x2-x*=x2-x*-(J(x1)TJ(x1)+A(x1))-1J(x1)Tr(x1))=(J(x1)TJ(x1)+A(x1)0-1(J(x1)TJ(x1)+A(x1)(x1-xI*)+J(x1)Tr(x1))=(J(x1)TJ(x1)+A(x1))-1(J(x1)Tr(xI*)-J(x1)T(r(x*)-r(x1)-J(x1)(x1-x*)))+((A(x1)-A(x*))(x1-x*)+A*x1-x*))

由定理1.2.12，见参考文献[1]，有

由条件J(x*)Tr(x*)=0和(8)不等式,有

‖J(x1)Tr(x*)‖=‖(J(x1)-J(x*))T(x*)‖ ≤σ‖x1-x*‖.

又有

其中

由微分中值公式有

由于‖J(x*+θi(x1-x*))‖F≤α

又由

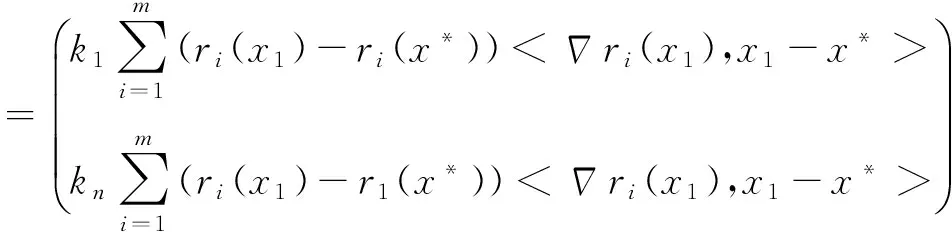
同样的，有

以及由条件不等式

从而，有

‖(A(x1)-A(x*))(x1-x*)‖≤L‖x1-x*‖2.

再由

因此，从(6)，有

因此，对k=0时，归纳法成立.一般的证明与上面相同，从而结论成立.

[1] 袁亚湘,孙文瑜.最优化理论与方法.北京:科学出版社,2007.

[2] 李董辉,章小娇,万中.数值最优化.北京:科学出版社,2005.

[3] Nocedal J, Wright S J. textsl{Numerical Optimization}. New York: Springer, 2000.

(责任编辑：于达)

Note about Gauss Newton Method

Zhao Shubo, Li Liwei

(Harbin Normal University)

The main difficulties of Least square problem with Newton′s method is Hesse matrix and the calculation of the second order items. In this paper, the first order of available obtained instead of the second order term of Newton′s method are studied . Therefore, a reduced order condition is introduced, and the nature of the Newton′s method is discussed. The convergence of this algorithm is proved to the second order and the superlinear under the condition.

Gauss Newton method, Convergence

2016-04-31

*黑龙江省教育厅科学技术研究项目(11TJKJ25)

O242

A

1000-5617(2016)03-0006-05