基于origin软件的初级像差仿真

赵 挺

(蚌埠医学院)



基于origin软件的初级像差仿真

赵 挺

(蚌埠医学院)

利用origin软件实现了初级像差图像的仿真，图像清晰细致，并与相关文献吻合.此方法无需复杂的编程，好学易用，在为理论和实验教学提供便利的同时，也加深了学生对像差现象认识和理解，提高了学习效果.

origin软件;初级像差 ;仿真

0 引言

像差，即实际光学系统成像偏离理论预期的现象，其降低了成像的清晰度和分辨率.由于光学实验对于设备、操作都有较高要求，往往无法在课堂上演示，从而影响了教学效果.让学生通过计算机对像差图像进行模拟，可以进一步加深学生对像差现象的认识和理解，也为传统的教学模式提供了较好的辅助手段，其中常见的是通过Matlab软件编程来实现[1]，但由于需要一定的编程基础，这又造成另一种学习上的困难.Origin软件界面友好、只需简单步骤即可实现对像差图像的仿真.整个过程无需复杂的编程、好学易用，便于教学演示和学生自学.

1 实验仿真

1.1 像差图像的仿真原理

光学系统的像差，可分为通过几何光学计算的几何像差和利用程函求出的波像差，后者主要通过光波波前的相位分布来体现，由于光波的相位一般并不影响光波的强度，故人眼不能直接观察到光波的相位分布.而相—幅转化可以通过使相位转化为振幅的方式，将相位的分布情况显示出来.根据泰曼—格林干涉仪和斐索干涉仪的原理[2]，两个相干点光源发出的光波,如图1所示相互干涉时，接受屏上出现互相平行的直线型干涉条纹，当两光源位置重合于O点时，接受屏上不出现干涉条纹.当将由像差引起的相位差，加载在其中一束光波上时，两束光波具有固定的相位差，接受屏上出现新的干涉图像，由于此相位差单纯由像差引起，故接受屏上出现的，即是根据相—幅转化原理，获得的像差图像.当加载不同的相位差时，就会得到对应的像差图像.

图1 光波干涉示意图

1.2 像差图像的光强分布[1][2]

图1中相干点光源S1、S2与接受屏上P点的距离分别为r1、r2，O点与接受屏的距离为L0，S1、S2所发出球面波在P点的复振幅分别为U1、U2，当S1、S2重合于O点时，r1=r2=r，则：

U1=U2=(A0/r)·ejkr

(1)

由图1可知，(1)式中的r为

(2)

I=U·U*=(U1+U2)·(U1+U2)*=I0/r2

(3)

(3)式表明屏上没有干涉条纹.在其中一束光波上加载像差W后，其在P点复振幅可表达为：

U3=U2·ejkw

(4)

取k=2π/λ，则此时屏上的光强分布为：

I=U·U*=(U1+U3)·U1+U3)*=(I0/r2)·cos2(πw/λ)

(5)

(5)式表示的即是像差图像中光强的分布情况.

在赛德尔坐标系中，设物点到光轴垂直距离为h、出瞳平面坐标为(ρ,θ)，则一个旋转共轴光学系统的初级波像差函数W，可通过以下多项式表示为[3]：

W(h,ρ,θ)=-Bρ4/4-Ch2ρ2cos2θ-Dh2ρ2/2+Eh3ρcosθ+Fhρ3cosθ

(6)

(6)式中的每一项都表示一种单色像差，其中-Bρ4/4代表球差、Fhρ3cosθ代表彗差、-Ch2ρ2cos2θ代表像散、-Dh2ρ2/2代表场曲、Eh3ρcosθ代表畸变， B到F为各项对应的赛德尔像差系数，代入(5)式后，可求得前4项像差图像的光强分布公式：

球差：

I=(I0/r2)·cos2(-Bπρ4/4λ)

(7)

彗差：

I=(I0/r2)·cos2(Fπhρ3cosθ/λ)

(8)

像散：

I=(I0/r2)·cos2(-Cπh2ρ2cos2θ/λ)

(9)

场曲：

I=(I0/r2)·cos2(-Dπh2ρ2/2λ)

(10)

1.3 像差图像的仿真实现

1.3.1 仿真步骤

将文献[4]描述的光学系统作为仿真对象，其前4项赛德尔像差系数见表1.设实际坐标系中，h′=15 cm、出瞳半径ρ′=3 cm.根据(6)式的成立条件，h′和ρ′需变换为赛德尔坐标，转化后物高h=0.478、出瞳半径ρ=3.07 cm.设光波波长为5.893×10-5cm、光强I0为1、L0为10 cm.

表1 前4项像差系数

根据前面的结论，确定如下仿真步骤：

(1)建立像差图像对应矩阵.

(2) 设置矩阵的维数(图像像素点)，以及x，y取值范围(图像显示范围).

( 3 ) 依据光强分布公式设定矩阵元，得到光强分布数值矩阵，并绘出图像.

以球面像差图像的仿真为例，打开origin9.0软件，依次点击File/NEW/Matrix，建立矩阵.选择Matrix/Set Dimension，在弹出的对话框中设定矩阵维数为(1000，1000)、x、y的取值范围都为(-3.07cm，3.07cm).由于在origin9.0中矩阵只能在直角坐标系下设定公式，故将(7)式，根据

x=ρcosθ,y=ρsinθ

(11)

化为

(12)

又因为旋转轴对称光学系统的性质，与接受屏中心O′的距离大于出瞳半径的区域，其光强应设定为零，故点击Matrix/Set Values，输入公式：

((x^2+y^2)^0.5>

3.07?0:((cos((-0.25*4.72e-5*pi*(x^2+y^2)^2)/5.893e-5))^2)/(x^2+y^2+100))，点击“OK”，得到光强分布数值矩阵.点击“plot/Count/Gary Scale Map”，获得球面像差仿真图像,如图2(a)所示.

作为比较，新建与上步相同矩阵，并依据(6)式球差对应项，输入公式：

((x^2+y^2)^0.5>3.07?0:(-0.25*4.72e-5*(x^2+y^2)^2))，并点击“plot/Count/Gary B/W lines+labels”，得到表示出瞳面球面(波)像差分布的等高线图，如图2(b)所示.

1.3.2 仿真结果

按照以上步骤，得到了前4种像差的仿真图像和对应的波像差分布图,如图2所示.

图2中各幅仿真图像都十分符合与之对应的像差分布图，这说明相—幅转化法准确显示了出瞳面上4种波前像差的分布情况.将图2中仿真图像与文献5、6中的图例相比较，两者也十分吻合.

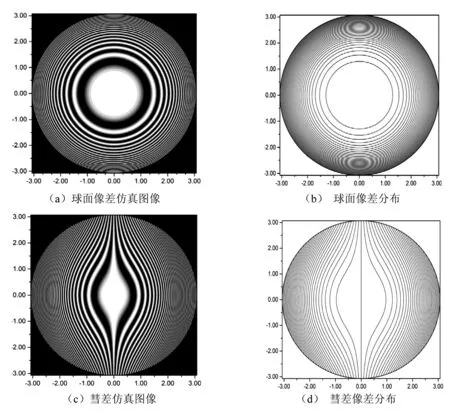
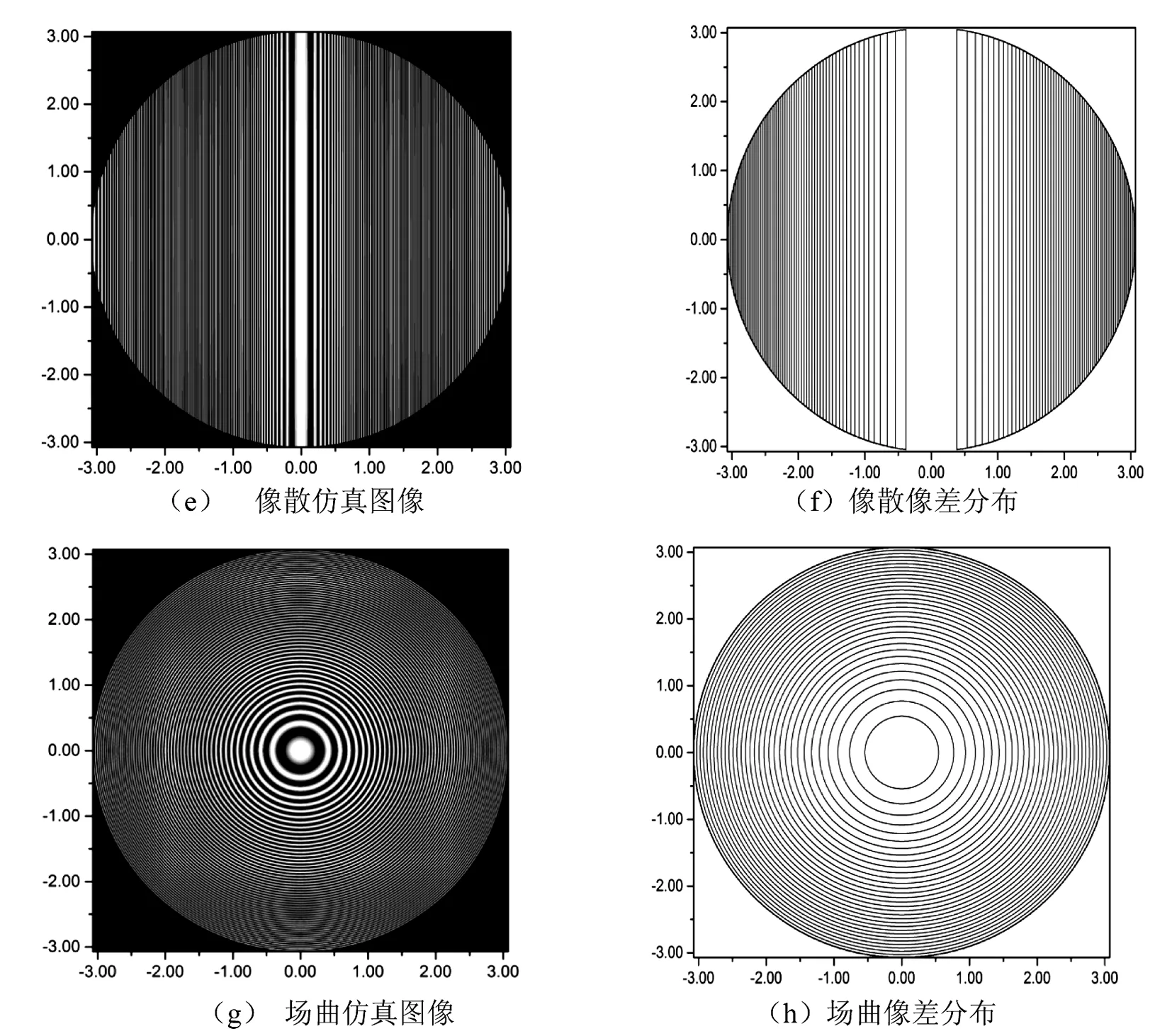
图2 4种像差的仿真图像和对应的波像差分布图

2 结束语

该文利用 Origin 软件，通过相—幅转化法对初级像差进行了仿真.生成了清晰细致的仿真图像，并与文献十分吻合.整个过程快速简便，为教学提供了便利. 也可安排学生自学此方法，让学生在阅读、调试、分析的过程中，加深对像差现象的认识和理解，激发学生的学习兴趣，提高其学习效率.

[1] 曲伟娟. 基于Matlab的光学实验仿真[D].西北工业大学,2004.39 -42.

[2] 杨国光.近代光学测试技术[M].杭州,浙江大学出版社,1997.22-26.

[3] 马科斯·玻恩,埃米尔·沃耳夫.光学原理[M].北京:电子工业出版社, 2005.193-205.

[4] 何乃宽,余虹.高等光学习题集[M].大连:大连工学院出版社,1988.261-266.

[5] Wyant J C，Creath K. Basic Wavefront Aberration Theory for Optical Metrology[J]. APPlied and OPtical Engineeirng, 1992，31(11):22-28，32-34.

[6] 威尔福特 W T. 对称光学系统的像差[M].北京:中国科学院出版社, 1974.86-104.

(责任编辑：季春阳)

A Study of Primary Aberration Simulation-Based on the Origin Software

Zhao Ting

(BengBu Medical College)

With the help of origin software, the primary aberration image is simulated, and the result of the simulation is also in good compliance with the relevant literature. It does not need complex programming, and it is easy to be learned and used. At the same time, origin software provides convenience for the theoretical and experimental teaching and deepens the understanding of the aberrational phenomenon for students , and it does a good turn to learning effect.

Origin software; Primary Aberration; Simulation

2016-05-22

O435.2

A

1000-5617(2016)03-0029-03