《参数方程复习》课例研究

张新华

（哈尔滨市第五十九中学 黑龙江哈尔滨 150030）

《参数方程复习》课例研究

张新华

（哈尔滨市第五十九中学 黑龙江哈尔滨 150030）

《极坐标与参数方程》是高中人教版教材选修4-4的主要内容， 在高考中考察的难度不大，学生容易入手。对于我们普通高中的学生来说，是能得分的。也是十分珍贵的。为此，我们备课组选择了《参数方程复习》一课作为研讨课。

在最初备课时，我想复习要全面。但是一节课的时间，内容太多学生不易接受。所以，我确定了复习的重点：直线的参数方程中t的几何意义的运用以及圆锥曲线参数方程的简单应用。为了能使这节课有实效性，我还向其他老师请教。这些老师的话让我深受启发：“教师通过引导，让学生主动参与到学习活动中”“高三复习要面向高考，精选高考题作为例题……”这些老师耐心、细致、专业的指导，为我这节课的成功奠定了基础。

下面是这节课的课堂实录（节选）

一、创设情境

师：请大家观察前面的两个问题，在题设上有什么相通之处？

过点M（-1，2），与曲线C： y2= 4x 有两个交点A、B 求：

判断曲线C与直线 L的位置关系

生：都有圆锥曲线，都有直线的参数方程

师：都与参数方程有关，对于参数方程，大家都能提出什么问题？

生：什么是参数方程？，为什么学习参数方程？······

师：概括一下同学们的问题：

第一、什么是参数方程。第二、常见曲线的参数方程有哪些。第三、为什么要建立参数方程

设计意图：通过问题引出本节课的主要内容，为本节课的学习指明了方向。

二、尝试概括

什么是参数方程、常见曲线的参数方程（略）

三、探究归纳

师：看前面提出的问题：

过点M（-1，2），与曲线C： y2= 4x有两个交点A、B

（3）

（4）线段AB的中点P的坐标

首先思考不用参数方程的知识该怎样解？

生：联立方程，求交点坐标，再求解。

师：学了参数方程后，又能怎样解？

生：把直线的参数方程代入抛物线，求A、B两点对应的参数

师：请同学们动笔计算，请一名同学到黑板运算。

与圆锥曲线交于两点A、B，且A、B对应的参数分别为21,tt 则③线段AB的中点对应的参数

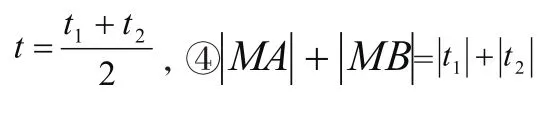
设计意图：通过一道例题，把直线参数方程中t的几何意义的运用的常见问题及解法进行归纳总结，对我们学生来说非常必要，有助于学生对知识的梳理与掌握。

师：再来看其它曲线参数方程的应用问题，怎样解决?

直线x+2y-2=0，点P在椭圆上，求P到直线距离的最大值。生：利用椭圆的参数方程设点P的坐标P( )θθ sin2,cos3

师：再看下面的变式题，怎样解？

生：设出点P的坐标，表示出2x+y

师：留作课后完成

师：通过这两题，谁能总结一下求圆锥曲线上与动点有关的最值问题的一般做法？

生：圆锥曲线上与动点有关的最值问题，一般做法：

（1）写出圆锥曲线的参数方程，把两个变量转化为一个变量。

（2）三角恒等变形，转化为求三角函数最值问题。

（3）写出最值、范围等。

设计意图：强调解题步骤，强化解题方法，为后面的例3做铺垫。

四、应用提升

师：根据目前我们对参数方程知识的掌握，对下面的题设

你能提出什么样的问题？生1： 相交求弦长……

生2：求椭圆上的点到直线的最大距离……

师：什么样的问题选择直线的参数方程来解，什么样的问题选择圆锥曲线的参数方程来解？

生：求弦长等问题用直线的参数方程来解，求最值问题选择圆锥曲线的参数方程来解。

设计意图：这个问题是开放性的，只有题设，学生自己提出问题。如果学生对前面的两个例题掌握了，就能仿照例1、例2那样提问。这既是对本节知识的检验，也是对本节知识的应用于提升。