考虑车轨耦合作用的车体动力吸振器减振性能研究
2016-12-15文永蓬尚慧琳徐小峻
文永蓬, 李 琼, 尚慧琳, 徐小峻
(1. 上海工程技术大学 城市轨道交通学院,上海 201620; 2. 上海应用技术学院 机械工程学院,上海 200235)
考虑车轨耦合作用的车体动力吸振器减振性能研究
文永蓬1, 李 琼1, 尚慧琳2, 徐小峻1
(1. 上海工程技术大学 城市轨道交通学院,上海 201620; 2. 上海应用技术学院 机械工程学院,上海 200235)
以降低城市轨道交通车辆车体的垂向振动为目的,建立了包含动力吸振器的车辆和轨道垂向振动的耦合模型,获得了耦合模型的垂向振动特性,进一步明确了轨道系统对车体垂向振动特性的影响,讨论了载客量和车速的变化对动力吸振器减振性能的影响,重点研究了考虑轨道系统影响后动力吸振器的设计方法,提出了一种新颖的考虑车速变化以及速度区间运行概率的动力吸振器的减振性能评价指标(DVA减振指标)。结果表明:轨道系统使轨道车体振动的峰值频率发生微小的偏移,改变了轨道车辆振动系统的振动特性,使车体垂向振动加剧;在车轨耦合作用下,动力吸振器的设计要综合考虑动力吸振器质量和设计频率的匹配,设计频率的阈值决定了动力吸振器是否减振,最佳设计频率决定了动力吸振器能否获得较好的减振效果。该项工作对包含动力吸振器的轨道车辆振动性能评价和分析具有重要的参考价值。
车轨耦合;垂向振动;动力吸振器;减振;DVA减振指标
近年来,随着城市轨道交通在我国飞速发展,轨道车辆振动带来的乘客乘坐舒适度问题也凸现出来。轨道不平顺引起的轮轨相互作用力经过一系和二系弹性悬挂传向车体从而引起车体的振动,车体下方的减隔振性能对乘客的舒适程度有重要的影响,因此,对车体减振装置的研究就显得非常有必要。
目前,国内外学者对轨道车辆建模进行了大量研究[1-5]。REMINGTON等[1]建立了轮轨接触模型,将车辆简化为单个车轮,轨道简化为Euler梁,为轮轨模型的研究奠定了基础;翟婉明等[2-5]建立了车辆与轨道系统的耦合模型,将车辆简化为多自由度刚体模型,将轨道看作是Timoshenko梁,考虑弹性钢轨的影响,发现系统的振动形态和数值大小上均存在一定差异,车辆-轨道一体化的动力学模型建立为正确评价与分析轨道车辆的振动性能提供重要的参考价值。为了降低轨道车辆的垂向振动,还有学者在已有的轨道车辆模型基础上引入动力吸振器[6-13]。TOMIOKA等[6]在转向架之间安装绳索作为动力吸振器,能够明显降低车体的弯曲振动,从而提高了车辆的运行品质;GOODALL等[7]在轨道车辆车体下方安装动力吸振器,采用主动控制器抑制了车体的弯曲变形,改善了乘客舒适度;曾京等[8]对有动力吸振器减振的研究中认为采用动力吸振器能够在一定程度上抑制车体垂向振动,而针对动力吸振器的设计没有提出具体的设计方法,仅指出适当增大动力吸振器质量、刚度和阻尼来提高减振效果,对动力吸振器的应用存在一定局限性。周劲松等[9-13]采用弹性车体模型对车体动力吸振器进行了系统而深入的研究,引入了车辆运行平稳性指标对车体动力吸振器的减振效果进行评价,得出动力吸振器能够使车辆的运行平稳性达到优级。总的来说,以往的研究中,对动力吸振器的设计往往忽视车辆-轨道的耦合,轨道系统对车体振动低频的改变从而引起动力吸振器减振性能的改变未予以重视,因此缺乏车轨耦合下车体动力吸振器具体的设计步骤和针对性的减振性能评价方法。
有鉴于此,本文考虑了轨道系统对车体垂向振动的影响,根据Lagrange方程,利用赫兹线性接触理论,建立了将动力吸振器安装在车体下方的车轨耦合模型;考虑了载客量和车速的变化,对比了传统模型、耦合模型的车体垂向振动响应;考虑车轨耦合作用对动力吸振器的设计方法和步骤进行了研究,对不同载客量和车速工况下的动力吸振器减振性能进行了分析,考虑车速变化以及速度区间运行概率,提出了一种新颖的动力吸振器的减振性能评价指标,对车体动力吸振器的减振效果进行评价。
1 包含动力吸振器的车轨耦合模型
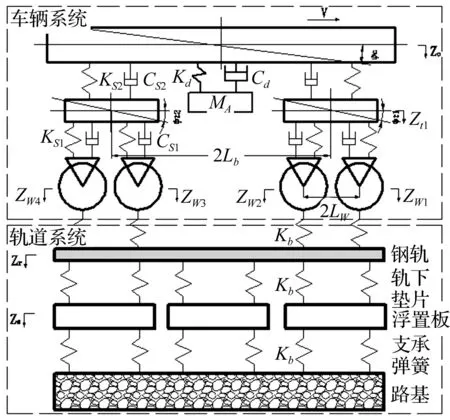
图1 含动力吸振器的车轨耦合模型Fig.1 The vehicle-track coupling model with DVA
如图1为包含动力吸振器的车轨耦合模型,该模型包括两个部分:车辆系统和轨道系统,动力吸振器安装在车体下方中部。车辆系统中,车身浮沉和点头运动有两个自由度、前后转向架浮沉和点头运动有四个自由度、车轮浮沉运动有四个自由度和位于车体底架中部的吸振器的浮沉运动有一个自由度,共十一个自由度;轨道系统中,为了简化计算,采用钢轨、短型浮置板的双自由振动模型,这是因为城市轨道交通的地面线大多采用有砟轨道,有砟轨道与短型浮置板轨道具有一定的相似性,采用短型浮置板轨道不仅能够反映短型浮置板轨道的振动特性,也能一定程度上体现有砟轨道对车辆系统的影响。其中Zc、Zt1、Zt2分别表示车身、前转向架和后转向架的垂向位移,φc、φ11、φ12分别为前转向架和后转向架的点头角,ZW1、ZW2、ZW3、ZW4分别为一轴、二轴、三轴、四轴的垂向位移,Zr、Zs分别为钢轨和轨道浮置板的垂向位移。其余参数如表1所示。

表1 某地铁车辆、轨道和动力吸振器的参数
2 耦合模型的求解
根据Lagrange方程,获得耦合模型中车辆系统的动力学表达式:
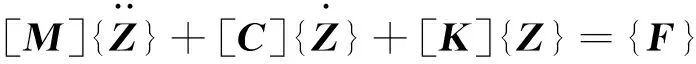
(1)
式中:{Z}为位移阵,{M}为质量阵,{C}为阻尼阵,{K}为刚度阵, {F}为轮轨力阵。
对式(1)进行傅里叶变换可得:
(-ω2[M]+jω[C]+[K])Z(ω)=[F(ω)]
(2)
轮轨接触力是轨道车辆振动的激励源。国内尚未建立城市轨道交通轨道功率谱分析式和应用标准,而美国轨道六级谱[4]与我国线路实际情况较为相似,因此,以美国六级轨道高低不平顺为车辆垂向振动模型的激励,轨道不平顺的空间功率谱密度Sv(Ω)为
(3)
式中:Ω为空间圆频率,单位为rad/m,Av为粗糙度系数,取0.033 9×10-4m2·rad/m,Ωc为截止空间圆频率,取0.824 5 rad/m。
轨道不平顺的时间功率谱密度为Gq(f)为
(4)
式中:u为车速,单位为m/s。
轮轨接触力本质上是非线性力,为了便于计算,工程上往往将轮轨接触力线性化,各轴轮轨接触矩阵根据赫兹线性接触理论[14-15]进行计算:
Fi=Kh(Zwi-Zri-qi)
(5)
式中:i=1,2,3,4,Fi为第i轴轮轨相互作用力,qi为第i轴处轨道不平顺度,Kh为轮轨接触刚度,Zwi为第i轴车轮的垂向位移,Zri为第i轴轮轨接触处钢轨的垂向位移。如果考虑车轨耦合作用,则Zri≠0;如果不考虑车轨耦合作用,则Zri=0,那么耦合模型则退化成十一个自由度的传统模型。
将式(5)进行傅里叶变换:
Fi(ω)=Kh(Zwi(ω)-Zri(ω)-qi(ω))
(6)
根据位移和力之间的关系,有
(7)
由式(6)、(7)整理可得:
(8)
式中:φw、φr、φc分别为车轮柔度,钢轨柔度,轮轨接触柔度,其中φc=1/Kh。
由于轨枕离散、浮置板离散支撑等等原因,轨道在纵向上并不是均匀支撑的,四个轮对接触处钢轨的柔度系数是不一样的,为了简化计算,将轨道假定简化为连续且均匀的弹性系统,因此,车轮柔度φw可根据车辆1/8模型[16-17]获得,并且,论文建立的是刚体模型,不考虑车辆各部件的弹性变形,尽管这种简化不能计算轨道响应特征,但是能够更加方便引入各轮对之间存在时滞关系。鉴于篇幅限制,φw直接给出:
(9)
其中:
(10)
B=
(11)
目前来讲,浮置板轨道具有较好的隔振效果[18],应用较为广泛,将钢轨简化为连续支承的无限长Euler梁,假设钢轨受到简谐激振力Fejωt,钢轨柔度φr根据短浮置板轨道模型[19]获得:
(12)
式中:τ称为波数,是式(13)的解。
(13)
其中:Kf=Kp(Kb-Msω2)/(Kp+Kb-Msω2)
由式(8)~(13),单节车厢的轮轨接触力阵为:
(14)
式中:
第二轴、第三轴、第四轴轮对的不平顺输入激励与第一轴轮对不平顺输入激励存在时滞关系,因此,车辆的激励矩阵为:
[q1(ω)q2(ω)q3(ω)q4(ω)]T=[Q]q1(ω)
(15)
其中:车轮频域内的时滞矩阵为:
(16)
式中:T2=2Lw/u,T3=2Lb/u,T4=2(Lw+Lb)/u。
若令[H(ω)]为车轨耦合振动系统的频响特性阵,可表示为:
[H(ω)]=[Z(ω)]/q1(ω)
(17)
式(17)反映轨道不平顺激励q1(ω)为输入,各质量垂向位移阵[Z(ω)]为输出的频响特性,再由式(5)、(14)、(15)可得:
(18)
综上所述,可以得到考虑车轨耦合作用的车辆各自由度对于不平顺输入的位移频率响应函数矩阵:
[H(ω)]=[h1(ω) …hk(ω)]T
(19)
式中:hk(ω)为轨道车辆垂向振动位移Zk(ω)对应的频响特性,其中k=1,2,…,11。
(20)
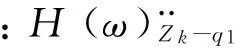
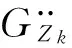
(21)
式中:Gq1(ω)为轨道不平顺激励q1(ω)的功率谱密度。
为了分析轨道车辆车体从ω1到ωn频率范围内垂向振动加速度功率谱密度,定义Gω1-ωn为垂向振动的加速度功率谱密度均方根值(以下简称加速度均方根值),用来反映车体的整体振动特性,由于车体振动的峰值频率主要在1 Hz左右,所以,在不影响精度的情况下取ω1-ωn为0.1~3 Hz,则:
(22)
3 车轨耦合下车体的垂向振动特性
3.1 轨道系统对车体垂向振动的影响
将不考虑轨道影响的模型称为传统模型,该模型将轨道视为刚体,对钢轨的弹性不考虑,仅仅考虑车辆系统;而考虑轨道的影响的模型称为耦合模型,该模型考虑车辆系统与轨道系统之间的耦合作用。令城市轨道车辆运行车速为80 km/h,根据上述模型获得轨道车辆车体传统模型、耦合模型垂向振动功率谱对比图,如图2所示。
在图2(a)中,车体垂向振动在频段Ⅰ和频段Ⅲ被抵消,而在频段Ⅱ产生叠加,这是因为考虑车轨耦合作用,钢轨的柔度不再被忽略,系统的振动特性发生了一定改变;图2(b)是常数坐标下的垂向振动功率谱对比图,图上可以清晰的看出在频段Ⅱ传统模型、耦合模型的差异,耦合模型的车体振动峰值明显高于传统模型,车体振动相应的峰值频率也发生了偏移,这与文献[4]不同,这是因为:可将车辆系统和轨道系统视作两个振动系统,其振动近似为两个叠加的波,根据波的叠加原理,在波的叠加区域内各点的振动的物理量等于各列波在该点引起的物理量的矢量和,振动过程中两个系统的振动可能叠加,也可能相互抵消,轨道系统能否吸收车辆的振动与两个振动系统的频率和波长有直接关系,因此,考虑弹性钢轨的影响,其系统的振动形态和数值大小上都存在一定差异[2],这种差异在大铁路车辆上分析车体振动的影响较小;但是,由于城市轨道交通车辆参数的敏感性,车轨耦合作用的影响不可忽略,考虑轨道系统的影响,城市轨道车辆的振动特性发生变化,导致车体振动加剧,振动的能量转移到1.5 Hz附近。
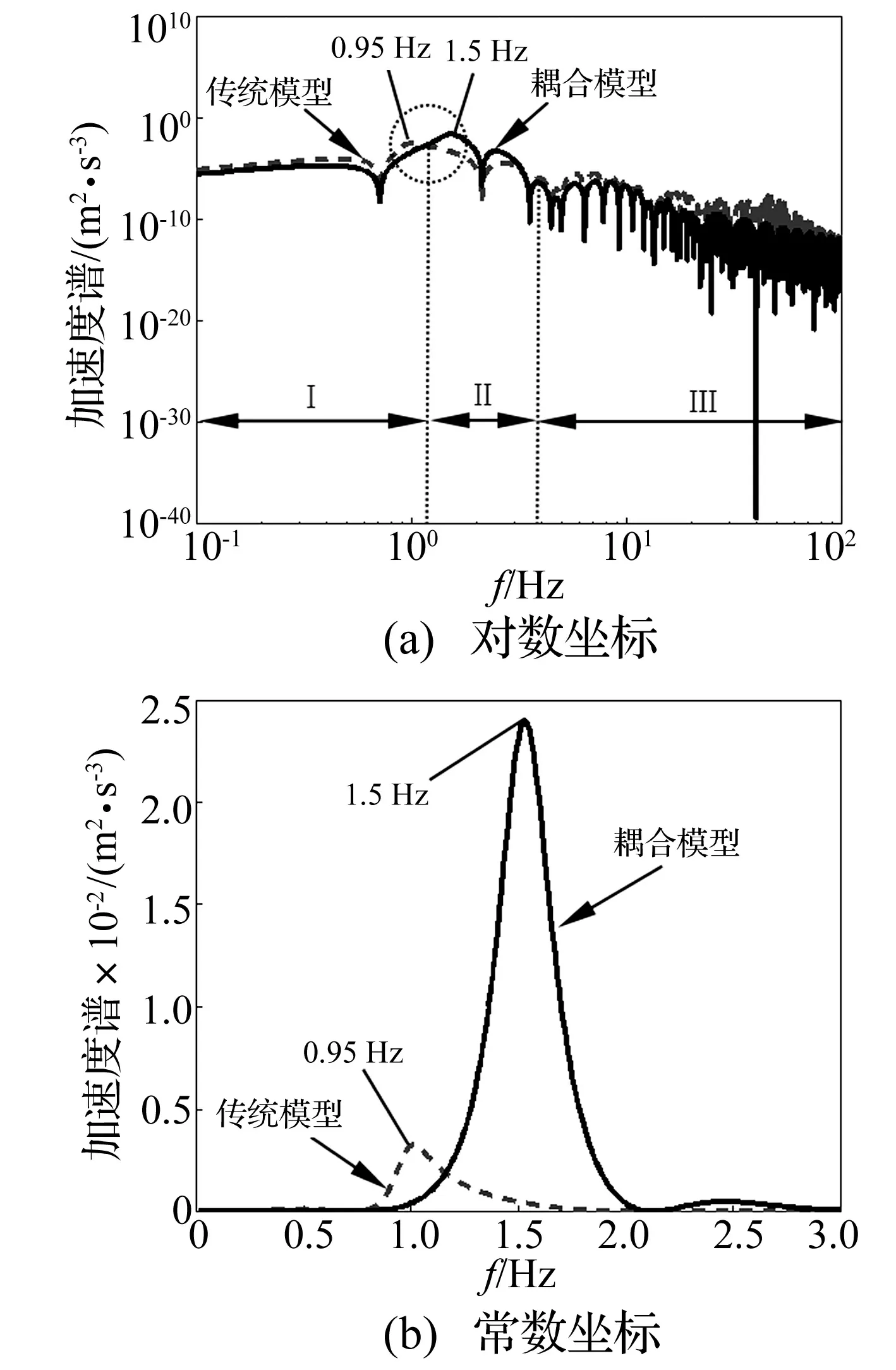
图2 车体垂向振动传统模型、耦合模型加速度功率谱对比图Fig.2 Comparison of the vertical vibration characteristic of vehicle body between the traditional model and the coupled model
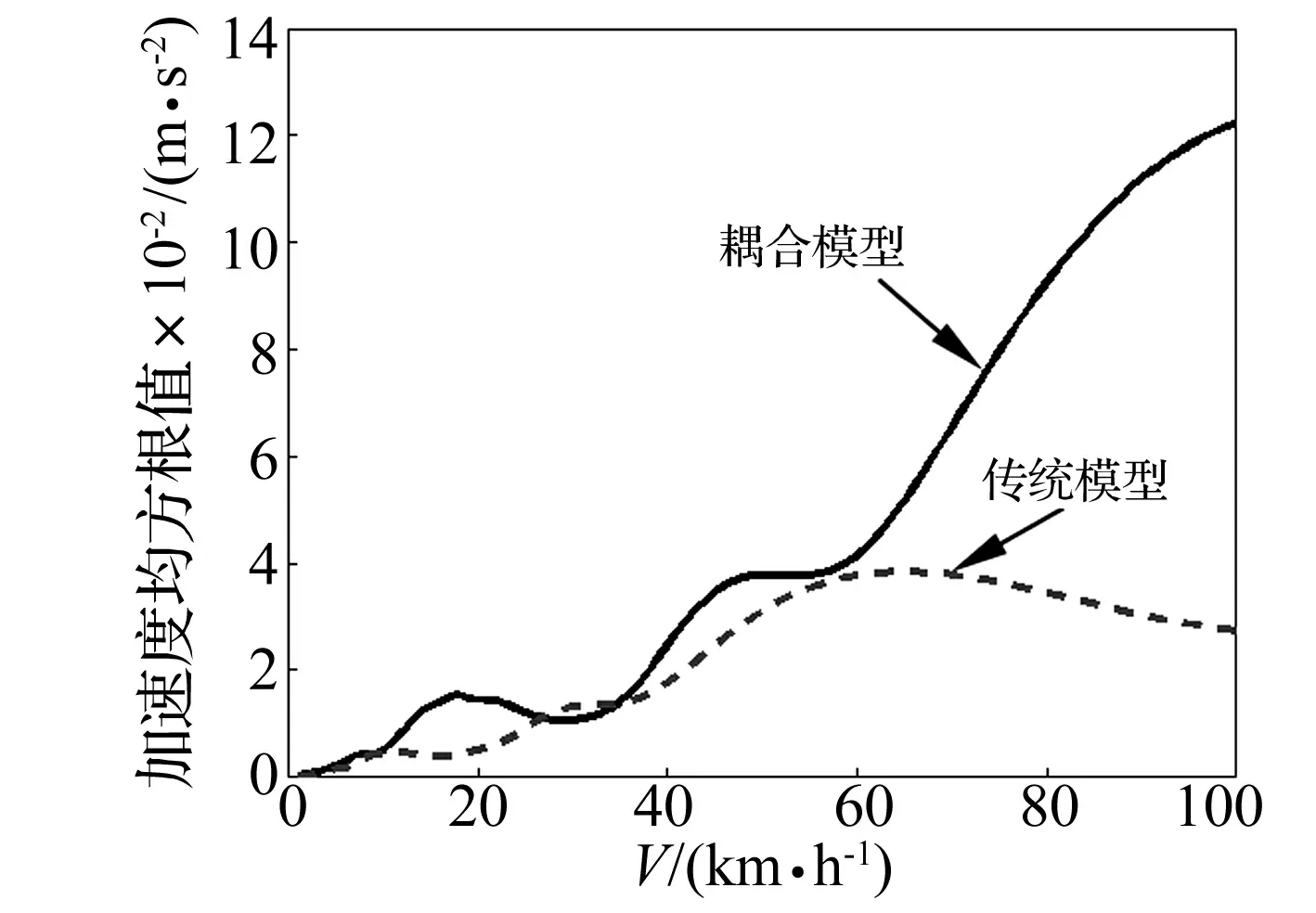
图3 车辆运行速度对车体垂向振动的影响Fig.3 Effects of speed on vertical vibration of vehicle body
图3为传统模型、耦合模型车体垂向振动的加速度均方根值,由式(22)计算获得,反映车体在整个分析频段内的整体振动情况。由图3可知:轨道车辆在运行过程中,车体垂向振动存在共振速度,车辆的垂向振动随运行速度不是呈单调增加的趋势,而是在共振速度处出现局部峰值[8,20]。本论文中涉及的城市轨道车辆,在传统模型研究中,在60 km/h附近达到共振速度,因此,车辆垂向振动达到局部峰值。此外,当车辆行驶速度在0~60 km/h阶段传统模型、耦合模型车体垂向振动差别不明显,但是,60 km/h以后,随着车辆运行速度的提高,考虑轨道系统的耦合模型车体垂向振动增加明显。因此,对车体减振的研究,必须要充分考虑轨道系统的影响。
3.2 载客量变化对车体垂向振动的影响
城市轨道交通车辆运行过程中,载客量经常发生变化。一般将载客情况分为四种:空载(AW0)、轻载(AW1)、满载(AW2)和超载(AW3)。为了保持车体地板平面高度不变,二系悬架刚度Ks2随载客量变化同时改变,仿真时令Ks2/Mc为定值。
当车速为80 km/h时,如图4为载客量变化对传统模型、耦合模型车体垂向振动的影响。由图4(a)可知:针对传统模型,当载客量从AW0到AW3逐渐增加时,车体的垂向振动逐渐减弱,而且,车体的振动峰值频率也越来越小。由图4(b)可知,针对耦合模型,当载客量增加时,车体的垂向振动峰值略微增加,但是,振动峰值频带逐渐变窄,耦合模型车体的振动峰值频率基本保持不变,始终维持在1.5 Hz附近,不随载客量的改变而改变。
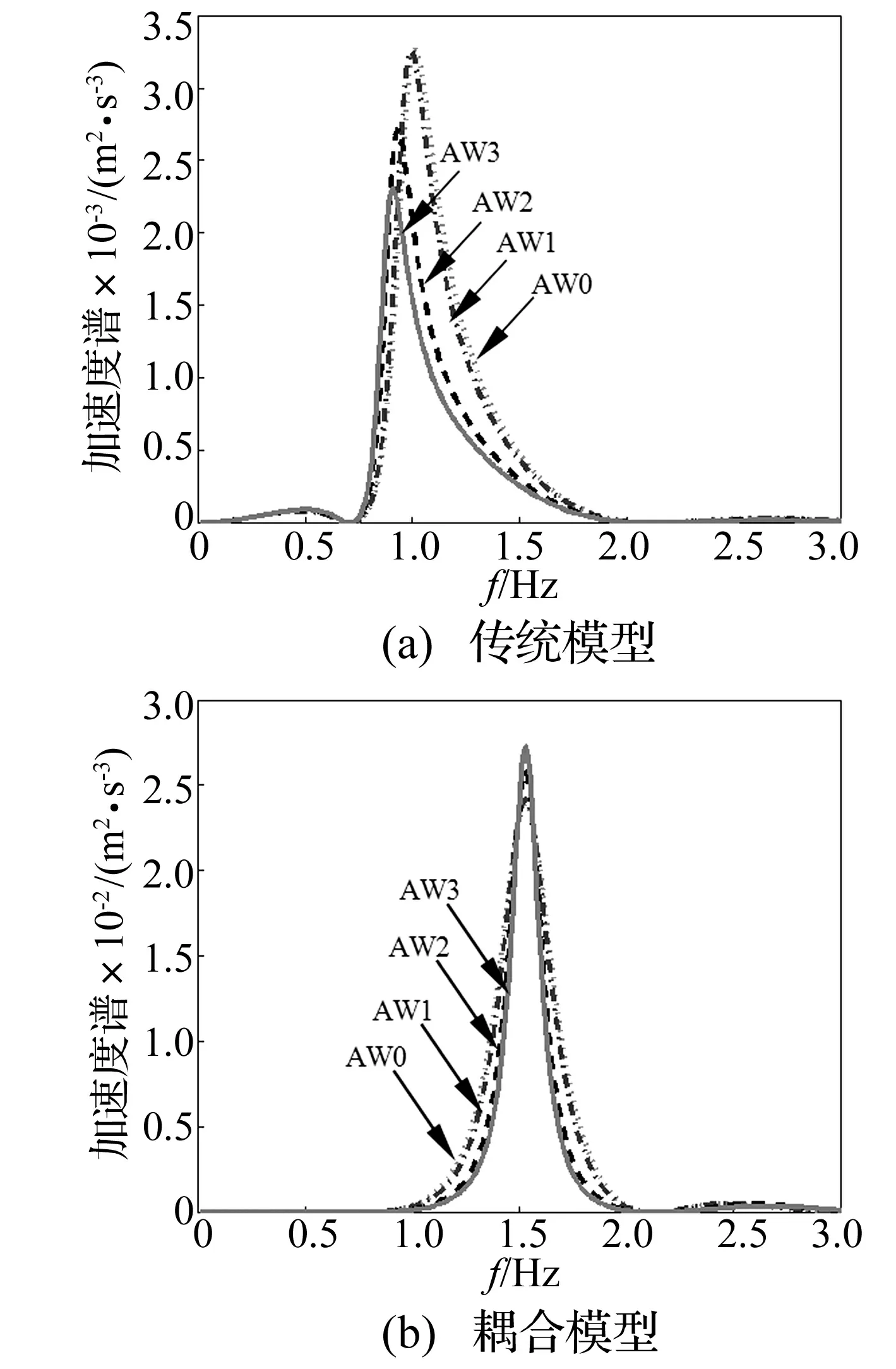
图4 载客量变化对传统模型、耦合模型车体垂向振动的影响Fig.4 Effects of passenger volume change on vertical vibration of vehicle body between the traditional model and the coupled model
3.3 速度变化对车体垂向振动的影响
城市轨道交通车辆显著特点之一是车辆的启动、加速、制动、过弯非常频繁[21],因而车速的变化也很频繁,对车体垂向振动存在一定影响。
令车辆运行在AW0工况,速度变化对传统模型、耦合模型车体垂向振动的影响,如图5所示。由图5(a)可知,传统模型,在50 km/h到80 km/h这个速度区间,车体的垂向振动峰值频率基本在0.95 Hz附近,随速度的增加振动峰值频率变化较小, 60 km/h时垂向振动最剧烈,80 km/h垂向振动较小,这是因为论文这组城市轨道车辆参数下,60 km/h附近达到共振速度,而在80 km/h恰好是在共振速度的一侧,处于下降阶段(见图3),因此尽管随速度的增加趋势上垂向振动是增加的,但是局部数值上却较小。
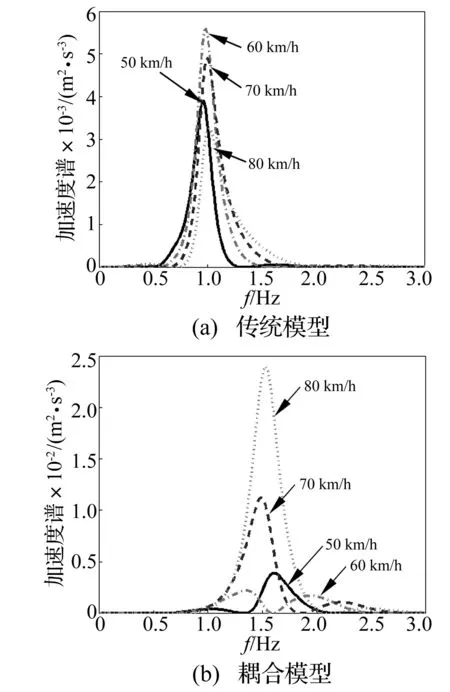
图5 速度变化对传统模型、耦合模型车体垂向振动的影响Fig.5 Effects of speed change on vertical vibration of vehicle body between the traditional model and the coupled model
由图5(b)可知:耦合模型明显比传统模型振动剧烈,这与图3的结果是一致的;此外,车辆在同样的速度变化下引起车辆垂向振动的峰值频率发生较大改变,60 km/h时垂向振动最小且峰值频率出现两处,即1.3 Hz处、2.0 Hz处,垂向振动最剧烈的80 km/h 峰值频率出现在1.5 Hz,这一现象文献[22]也有报道,车辆运行中,加速度谱值并非单调变化,车辆运动过程中属于多点激励,不同轮对之间的响应会有叠加或者抵消,而车速影响了轨道谱的激励,影响了各激励的时间差和激励的空间分布[22];因此,可以认为车速的改变影响轨道不平顺激励的功率谱密度,以及各轮对之间的时滞关系,并且,轨道系统作用使车体振动的峰值频率发生微小的偏移,从而改变了系统的振动特性,车轨耦合的作用加剧了车体垂向振动。
针对城市轨道车辆的特点,无论考虑载重的改变,还是车速的改变,轨道系统的影响都是不可忽略的,因此,下面的系统减振研究中,均考虑车轨耦合作用。
4 考虑车轨耦合作用的车体动力吸振器的设计
4.1 考虑车轨耦合作用的动力吸振器的设计方法
将轨道车辆车体视作主系统,为了要吸收车体的振动,在主系统的基础之上增加车体动力吸振器,这种简化后的二自由度“主系统-动力吸振器”振动模型如图6所示。
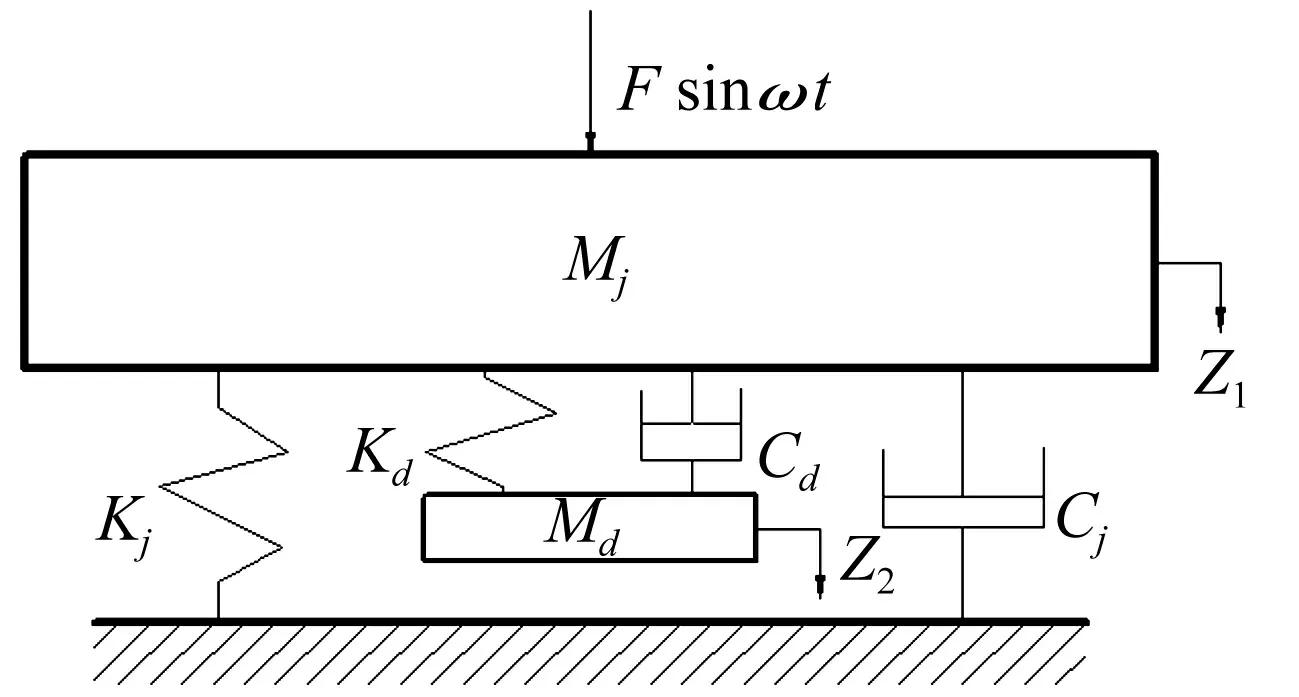
图6 二自由度“主系统-动力吸振器”振动模型Fig.6 Vibration model of two degree of freedom with the main system and dynamic vibration absorber
此模型可用下式描述:
(23)
式中:Mj、Kj、Cj分别代表主系统的质量、刚度、阻尼。为了简化计算,Mj近似为是车体的质量;Kj由忽略构架质量后的一系和二系悬架简化而来,即每个转向架下方的两对一系弹簧看做并联,忽略转向架的质量后与二系弹簧进行串联,将前、后两个转向架简化后的弹簧进行并联;Cj采用类似的简化方法。
动力吸振器设计过程中引入以下各项:
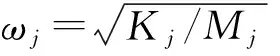
动力吸振器的同调条件[23]为:
(24)
根据式(24)可得动力吸振器的设计刚度:
(25)
整理 式(25)可得:
(26)
动力吸振器的阻尼条件[23]为
(27)
根据式(27)可得动力吸振器的设计阻尼:
Cd=2Mdωjζ
(28)
整理式(28)可得:
(29)
从式(26)和式(29)可知:只要确定动力吸振器和主振系质量比μ和主振系的固有频率fj,就能够获得动力吸振器的设计刚度Kd和设计阻尼Cd。
令ε为动力放大系数,则:
(30)
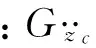
为了确定动力吸振器和主振系质量比μ,令车速为80 km/h,主振系的固有频率fj约为1.5 Hz(见图5(b)),获得不同质量比情况下,动力吸振器的动力放大系数频率特性图,如图7所示。图7(a)中,动力吸振器的动力放大系数的减振最优点并不在1.5 Hz处,减振最优点频率fdesign-opt与主振系的固有频率fj之差Δf,有
(31)
随着质量比μ的增加,Δf越来越大。当μ=0.2时,Δf3甚至为0.5 Hz。因此,为了提高动力吸振器在目标频率fj处的减振能力,令fdesign为动力吸振器的设计频率,可以近似认为:
fdesign=(1+μ)2fj
(32)
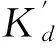
(33)
图7(b)为利用式(33)对动力吸振器刚度修正后的动力放大系数频率特性图,动力吸振器的减振最优频率集中在1.5 Hz,并且带宽也变宽了,从而在目标频率fj处的减振能力获得较大提升。
在图7中,随着质量比μ的增加,减振有效区域变大,动力放大系数减振最优点逐渐下降,吸振器的减振效果逐渐增强,这说明动力吸振器的质量越大,减振效果越好,但是,考虑到动力吸振器的对车辆限界的影响、经济性以及布置的难易程度,下面的研究中,均取μ=0.2。
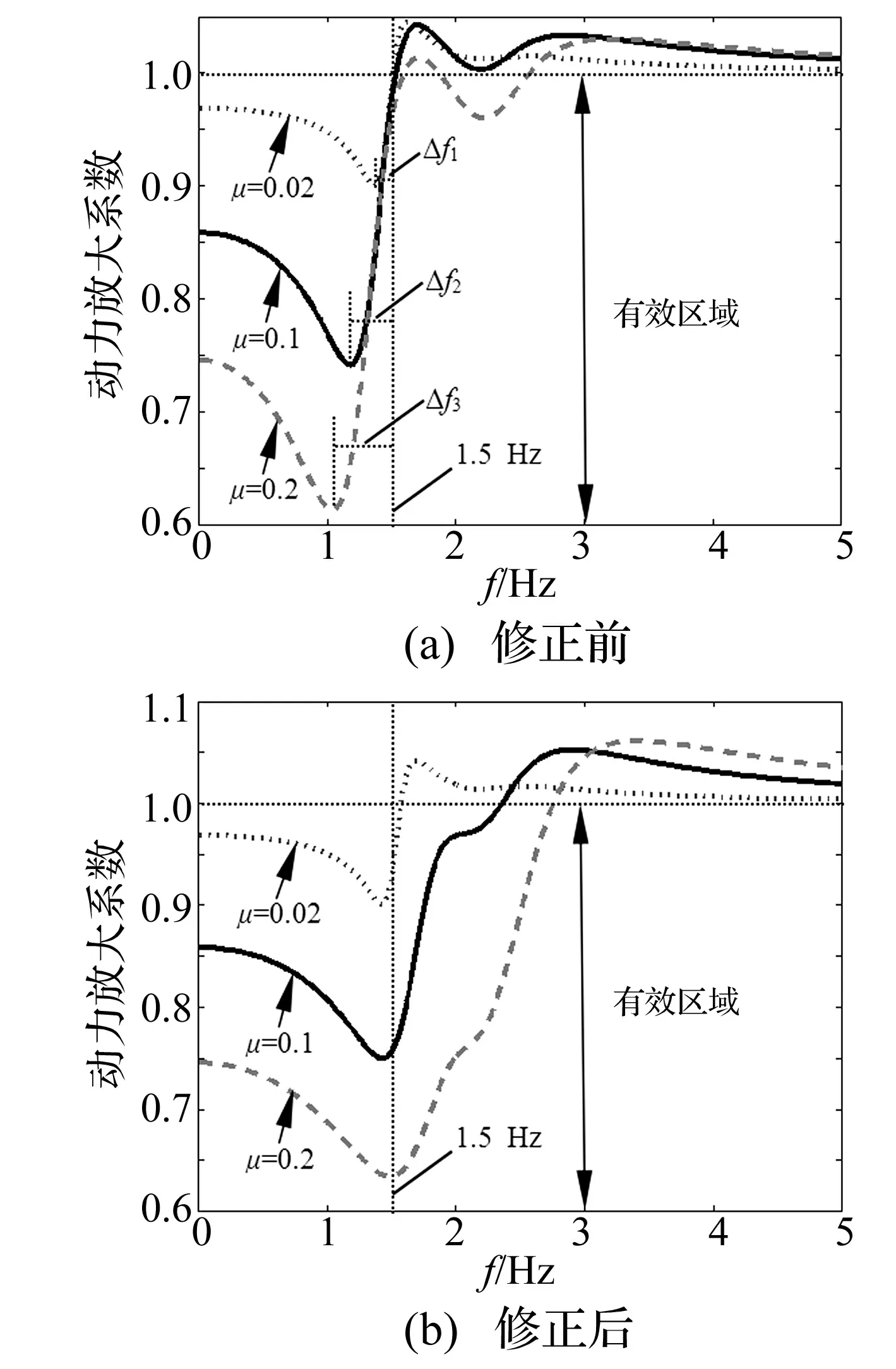
图7 不同质量比的动力放大系数频率特性图Fig.7 Frequency characteristics of dynamic magnification factor with different mass ratio
综上,轨道车辆车体动力吸振器参数设计的一般步骤为:
(1)根据车辆的实际情况和安全性等因素的考虑,确定动力吸振器和主振系质量比μ;
(2)根据车轨耦合模型,确定主振系的固有频率fj;
(3)修正动力吸振器的设计刚度Kd,提升目标频率fj处的减振能力。
4.2 动力吸振器在不同载客量工况下的减振性能
根据上述步骤,利用式(29)和式(33)设计的含动力吸振器的轨道车辆在车速为80 km/h时,在不同载客量工况下,动力吸振器表现出的性能是不同的,如图8所示。
由图8可知,随着载客量从AW0到AW3逐渐增加,在有效区域内1.5 Hz附近,尽管动力吸振器的减振效果变差,但是含动力吸振器的车辆的车体振动还是降低的,出现这一情况的主要原因是,随着载客量的增加,车体的重量增加,导致动力吸振器与车体的质量比μ相对减小,较小的μ的动力吸振器也能吸收一定的车体振动。
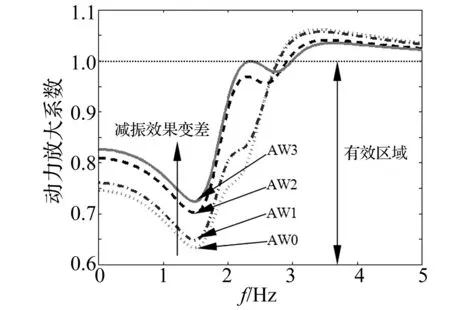
图8 不同载客量对动力吸振器减振性能的影响Fig.8 Effects of different passenger volume on vibration reduction performance of dynamic absorber
4.3 动力吸振器在不同车速工况下的减振性能
不同的车速工况下,轨道车辆车体具有不同的垂向振动峰值频率,根据图5(b),可以获得在50 km/h到80 km/h这个速度区间车体的垂向振动峰值频率,而不同的峰值频率动力吸振器的设计是不同的,因而,出现由于车速不同引出的五种动力吸振器的设计,如表2所示。
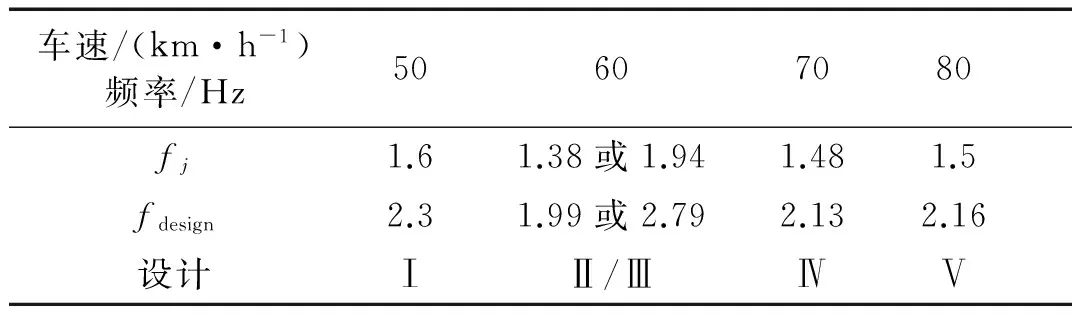
表2 不同速度下动力吸振器的设计频率
利用表2中数据,针对50 km/h到80 km/h这个速度区间,分别获得五种动力吸振器减振性能与车速的关系,如图9所示。由图9可知:在车体的垂向振动峰值频率处,五种设计的动力吸振器均能有效降低车体振动,分别降低34.2%、38.1%、35.3%、36.7%、36.5%。
为了考察动力吸振器在整个速度区间内的减振能力,选择针对60 km/h峰值处减振较好的设计Ⅲ和针对80 km/h峰值处减振较好的设计Ⅴ,获得整个速度区间内的加速度均方根值,如图10所示。由图10可知,这两种设计都具有一定的减振效果;此外,设计Ⅲ相比设计Ⅴ,在60 km/h具有较好的减振能力,在80 km/h具有较差的减振能力,这说明每一种设计针对特定的速度或者特定的频率才能发挥最佳减振性能,在其他速度时动力吸振器的减振性能并不是很好,因此,仅依靠峰值频率处的响应来评价动力吸振器在整个速度区间内的减振性能存在一定局限。
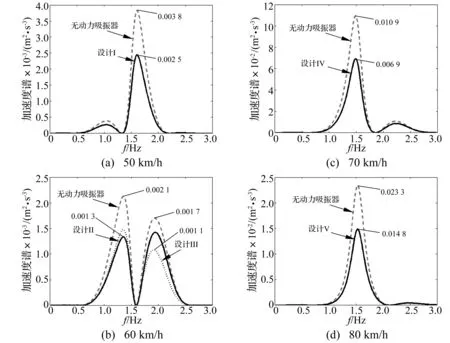
图9 五种动力吸振器减振性能与车速的关系图Fig.9 The relationship of vibration reduction performance and speed for the five kinds of DVA
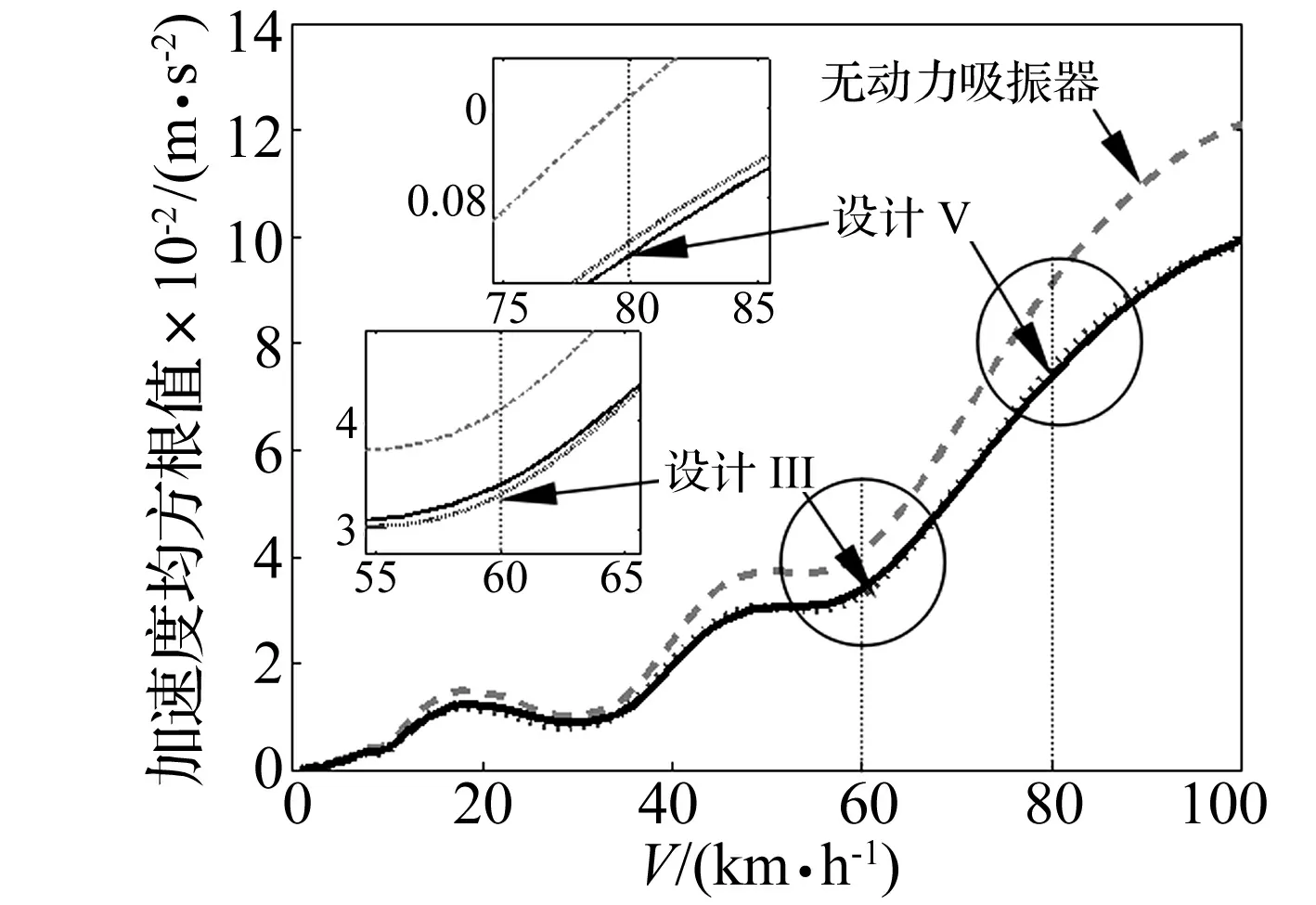
图10 设计Ⅲ、设计Ⅴ在各速度下的减振性能Fig.10 vibration reduction performance of design Ⅲ and design Ⅴ of V in various speeds
4.4 动力吸振器减振能力的验证
为验证论文方法的正确性和可行性,采用评价乘坐舒适性的Sperling平稳性指标[4,10]验证动力吸振器的减振能力,Sperling平稳性指标是学术界公认的评价车体平稳性的指标之一。
图11为设计Ⅲ、设计Ⅴ后车辆的Sperling指标与无动力吸振器的对比。由图11可知,随着车速的提高车辆的运行平稳性指标整体上呈增大趋势,而且,无论减振前、减振后车辆的运行平稳性指标都保持在优级(<2.5),这也证明了论文动力吸振器设计具有合理性。但是,采用Sperling评价指标,设计Ⅲ和设计Ⅴ区分不够明显,不能直观的反映动力吸振器的设计优劣,无法判断动力吸振器在整个速度区间内的减振性能;并且,从设计的角度,Sperling评价指标无法指导设计,这就是下面提出DVA减振指标的原因。
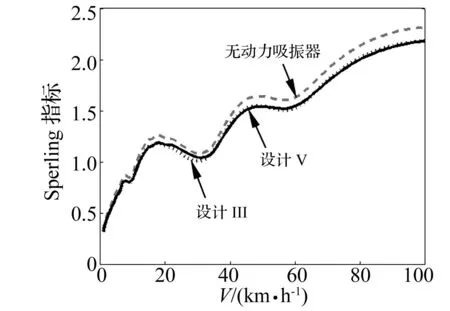
图11 采用设计Ⅲ、设计Ⅴ后车辆的Sperling指标Fig.11 Sperling stationary index of design Ⅲ and designⅤ of V in various speeds
4.5 DVA减振指标
为了进一步评价这五种动力吸振器的设计在整个速度区间内的减振能力,根据图10,令ΔAj为无动力吸振器时车体的垂向振动加速度均方根值曲线和含动力吸振器车体的垂向振动加速度均方根值曲线之间的面积之差,那么
(34)
式中:Gno-dva为无动力吸振器车体的垂向振动加速度均方根值,Gj为利用动力吸振器减振后的车体垂向振动加速度均方根值,vt为车辆t时刻运行速度,对于城市轨道车辆,一般取构造速度100 km/h。
定义无量纲数DVA为评价动力吸振器设计优劣的综合减振指标(简称DVA减振指标),则
(35)
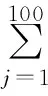
DVA减振指标综合考虑了轨道车辆速度的变化以及速度区间运行概率,能够直观地反映整个速度区间内动力吸振器的综合减振能力,根据定义,可知:当DVA>0时,动力吸振器在整个速度区间内综合减振能力较好,其值越大,综合减振能力越好;当DVA≤0时,动力吸振器的综合减振能力较差,当然,并不排除个别速度情况下有一定减振效果。
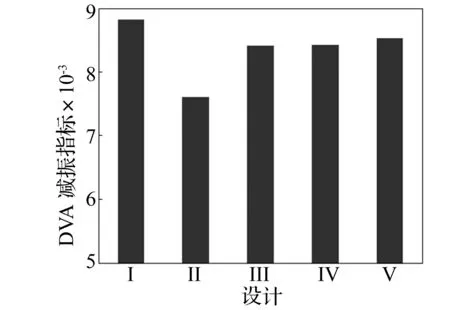
图12 利用DVA减振指标评价五种设计的优劣Fig.12 Evaluation of five kinds of design by using DVA vibration reduction index
图12是利用DVA减振指标评价表2中五种设计减振性能的优劣,由图12可知。这五种设计中,尽管设计Ⅰ垂向振动峰值减振最低,但是在整个速度区间内综合减振能力却是最好的。
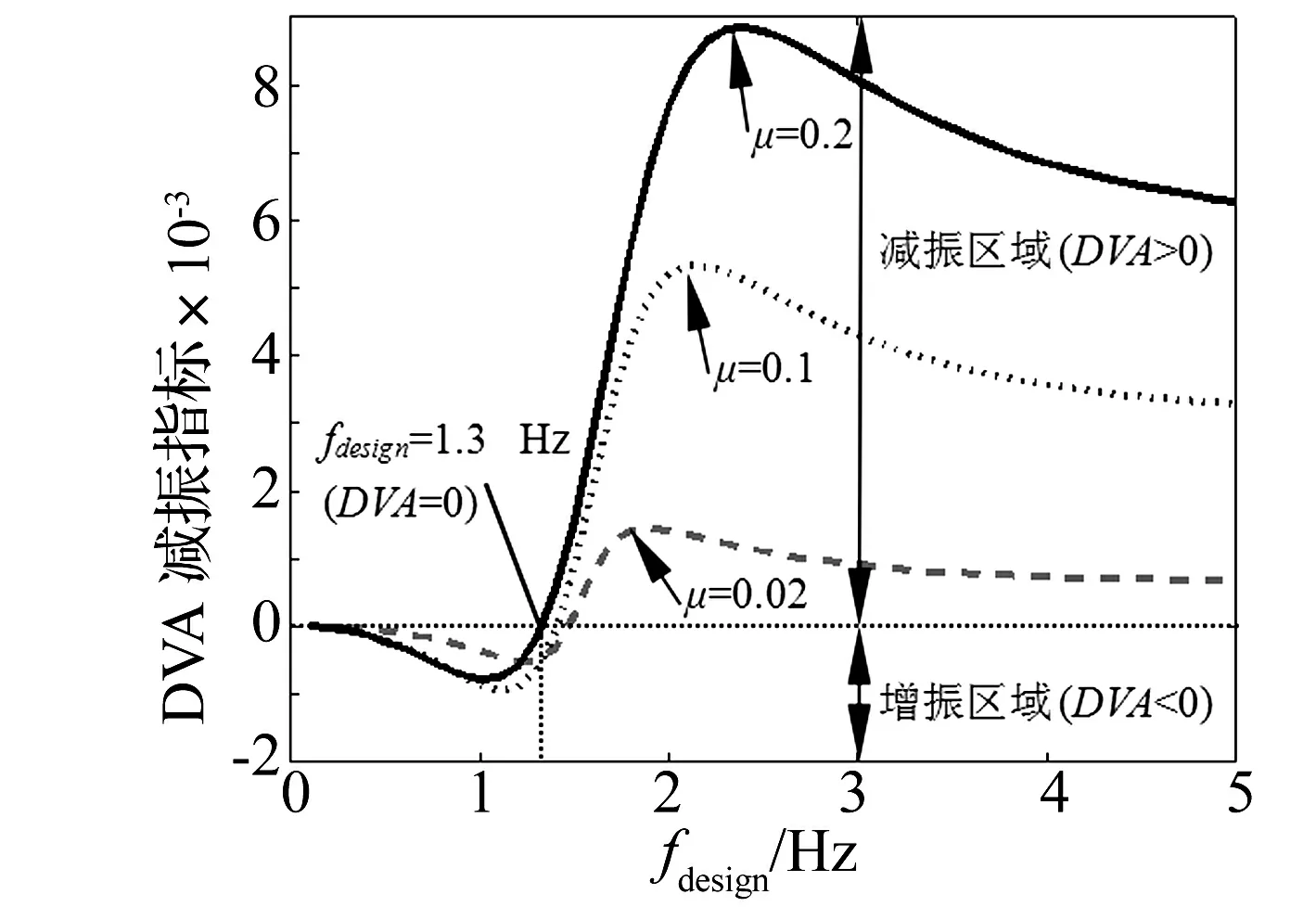
图13 设计频率和DVA减振指标的关系图Fig.13 The relationship diagram of the design frequency and DVA vibration reduction index
为了进一步利用DVA减振指标评价动力吸振器减振性能的优劣,考虑0~5 Hz的设计频率fdesign,获得fdesign和DVA指标的关系图,如图13所示。在图13中,对比了三种质量比μ情况下,遍历设计频率fdesign获得动力吸振器的不同的振动效果,发现:无论何种质量比μ,总存在动力吸振器的增振区域(DVA<0)和减振区域(DVA>0),动力吸振器是否减振以及能否取得较好的减振效果,都取决于设计频率fdesign的大小。随着质量比μ的增加,DVA=0的设计频率逐渐减小,当质量比μ增加到0.2时,设计频率fdesign为1.3 Hz,这就是说,只有大于这个设计频率的阈值1.3 Hz才能实现减振。此外,每一种质量比μ总存在一个最佳设计频率,动力吸振器的设计频率选取在此频率,才能实现减振的最大化,取得最佳的减振效果,比如μ=0.2时,在2.3 Hz处DVA减振指标最大,综合减振效果最好,这与图12的结果是一致的。当设计频率fdesign大于最佳设计频率,DVA减振指标曲线最终趋于平稳,减振效果变差但是仍然存在减振,这是因为设计频率fdesign增加会使动力吸振器的刚度和阻尼增大,尽管仍有减振效果,但是考虑到经济性以及加工的难易程度,不建议设计频率取值过大。
5 结 论
(1)轨道系统使轨道车辆车体振动的峰值频率发生微小的偏移,从而改变了轨道车辆振动系统的振动特性,并且,考虑车轨耦合的作用加剧了车体垂向振动,因此,对车体减振的研究,建议考虑车轨耦合作用。
(2)轨道车辆车速不同,其振动特性也不相同,综合考虑了轨道车辆速度的变化以及速度区间运行概率的DVA减振指标,能够直观地反映整个速度区间内动力吸振器的综合减振能力,当DVA>0时,动力吸振器对于轨道车辆振动系统处于减振状态,其值越大则减振性能越好。
(3)为了提高动力吸振器的减振效果,要综合考虑动力吸振器的质量和设计频率的匹配,即适当的增加动力吸振器质量的同时,还要格外注意设计频率的选取:设计频率的阈值决定了动力吸振器是否减振,最佳设计频率决定了动力吸振器能否获得较好的减振效果。
论文将轨道假定简化为连续且均匀的弹性系统,无法输出轨道响应特征,所建立的含动力吸振器的模型并非完整的车辆-轨道耦合模型,模型中车体被视作刚体,无法描述车辆的弯曲运动等模态,对车辆的振动特性的精确性还存在一定不足,并且动力吸振器的振动过程可能会引起车辆限界等问题,这对吸振器的悬挂元件工程设计造成一定困难,因此,建立完整的采用弹性车体的耦合模型进行动力吸振器的工程应用设计将成为我们下一步的工作目标。
[1] REMINGTON P J. Wheel/rail rolling noise,Ⅰ:Theoretical analysis Acoust[J].Soc.Am,1987,81(6):1805-1823.
[2] 翟婉明.铁道车辆在刚性及弹性轨道模型上的振动模拟分析[J].铁道学报,1999,(1):15-19. ZHAI Wanming. Vibration response analysis of railway vehicle in rigid and elastic track models [J]. Journal of the China Railway Society, 1999,(1):15-19.
[3] 陈果,翟婉明,蔡成标,等.传统车辆模型与车辆-轨道耦合模型的垂向随机振动响应分析及比较[J].铁道学报,1999(5):70-74. CHEN Guo, ZHAI Wanming, CAI Chengbiao, et al. Random vibration response analysis and compare of traditional vehicle model and vehicle-track coupling model[J]. Journal of the China Railway Society, 1999(5):70-74.
[4] 翟婉明. 车辆——轨道耦合动力学[M]. 3版.北京:科学出版社,2007.
[5] 翟婉明.车辆——轨道耦合动力学研究的新进展[J]. 中国铁道科学,2012,23(2):1-14. ZHAI Wanming. New advance in vehicle-track coupling dynamics[J]. China railway Science, 2012, 23(2):1-14.
[6] TOMIOKA T, TAKIGAMI T. Reduction of bending vibration in railway vehicle carbodies using carbody-bogie dynamic interaction[J]. Vehicle System Dynamics,2010(4):467-486. [7] FOO E, GOODALL R M. Active suspension control of flexible-bodied railway vehicle using electro-hydraulic and electromagnetic actuators[J]. Control Engineering Practice,2000(8):507-518.
[8] 曾京,邬平波,郝建华,等.铁道客车系统的垂向减振分析[J].中国铁道科学,2006,27(3):62-67. ZENG Jing, WU Pingbo, HAO Jianhua, et al. Analysis of vertical vibration reduction for railway vehicle systems[J]. China Railway Science,2006,27(3):62-67.
[9] ZHOU J, GOODALL R, REN L, et al. Influences of car body vertical flexibility on ride quality of passenger railway vehicles[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit,2009,223(5): 461-471.
[10] 周劲松.铁道车辆振动与控制[M].北京:中国铁道出版社,2012.
[11] GONG Dao, ZHOU Jinsong, SUN Wenjing. On the resonant vibration of a flexible railway car body and its suppression with a dynamic vibration absorber[J]. Journal of Vibration and Control,2012(2):649-657.
[12] 周劲松,宫岛,任利惠,等.铁道车辆弹性车体被动减振仿真分析[J]. 同济大学学报(自然科学版),2009,37(8):1085-1089. ZHOU Jinsong, GONG Dao, REN Lihui, et al. Simulation on passive vibration control of flexible carbody of railway passenger vehicles[J]. Journal of TongJi University (Natural Science),2009,37(8):1085-1089.
[13] 周劲松,张伟, 孙文静, 等. 铁道车辆弹性车体动力吸振器减振分析[J].中国铁道科学,2009,30(3):86-90. ZHOU Jinsong, ZHANG Wei, SUN Wenjing, et al. Vibration reduction analysis of the dynamic vibration absorber on the flexible carbody of railway vehicles[J]. China railway Science, 2009, 30(3):86-90.
[14] 刘学毅.车辆轨道路基系统动力学[M]. 成都:西南交通大学出版社,2010: 127-164.
[15] 王炯,吴天行. 浮置板轨道隔振性能研究[J]. 上海:上海交通大学学报,2007,41(6):1021-1025. WANG Jiong, WU Tianxing. On vibration isolation performance of floating slab track[J]. Journal of Shanghai Jiaotong University, 2007,41(6):1021-1025.
[16] 王炯. 浮置板轨道隔振性能研究[D]. 上海:上海交通大学,2007.
[17] 雷晓燕,张斌,刘庆杰,等. 列车-轨道系统竖向动力分析的车辆轨道单元模型[J].振动与冲击,2010,29(3):168-173. LEI Xiaoyan, ZHANG Bin, LIU Qingjie, et al. Model of vehicle and track elements for vertical dynamic analysis of vehicle-track system[J]. Journal of Vibration and Shock,2010,29(3):168-173.
[18] 吴川,刘学文,黄醒春,等. 短型浮置板轨道系统隔振性能研究[J]. 振动与冲击,2008,(8):74-76. WU Chuan, LIU Xuewen, HUANG Xingchun, et al. Study on effectiveness of short floating slab track system[J]. Journal of Vibration and Shock, 2008,(8):74-76.
[19] 李增光,吴天行. 浮置板轨道动柔度计算方法及隔振性能研究[J].振动工程学报,2007,20(3):207-212. LI Zengguang, WU Tianxing. Study on the vibration isolation performance of floating slab track using dynamic receptance method[J]. Journal of Vibration Engineering,2007,20(3):207-212.
[20] 池茂儒,张卫华,曾京,等. 铁道车辆振动响应特性[J]. 交通运输工程学报,2007,7(5):6-11. CHI Maoru, ZHANG Weihua, ZENG Jing, et al. Vibrant response characteristic of railway vehicle[J]. Journal of Traffic and Transportation Engineering, 2007, 7(5):6-11.
[21] 文永蓬,尚慧琳,董其炜,等.城市轨道车辆车轮轮缘磨耗分析[J].科技导报,2013,31(26):40-43. WEN Yongpeng, SHANG Huilin, DONG Qiwei, et al. Analysis on the wear of wheel flange for urban rail vehicle[J]. Science & Technology Review, 2013, 31(26):40-43.[22] 吕峰,林家浩,张亚辉,等. 车辆-轨道系统垂向随机振动的辛方法分析[J].力学学报,2008,40(3):381-387. LÜ Feng, LIN Jiahao, ZHANG Yahui, et al. Random vibration analysis of vehicle-track coupling systems using symplectic method[J]. Chinese Journal of Theoretical and Applied Mechanics,2008,40(3):381-387.
[23] 背户一登.动力吸振器及其应用[M]. 北京:机械工业出版社,2013.
Performances of dynamic absorbers for urban rail vehicle body considering effects of vehicle-track coupling
WEN Yongpeng1, LI Qiong1, SHANG Huilin2, XU Xiaojun1
(1. College of Urban Railway Transportation, Shanghai University of Engineering Science, Shanghai 201620, China;2. School of Mechanical Engineering, Shanghai Institute of Technology, Shanghai 200235, China)
To reduce vertical vibrations of urban rail vehicle body, a vehicle-track model with dynamic absorbers was established here, and the vertical vibration characteristics of the coupling model were derived. The effects of track system on the vertical vibration characteristics of the vehicle body were analyzed and the influences of passengers capacity and vehicle speed on the performances of dynamic absorbers were disscussed. The design method of dynamic absorbers considering the effects of track system was studied. Considering speed change and operating probability of vehicle speed range, a novel evaluation index called DVA vibration reduction index was proposed to evaluate the performances of dynamic absorbers. The results showed that due to track system, the peak vibration frequency of the urban rail vehicle body offsets slightly, and the vibration characteristics of the rail vehicle system vary, the vertical vibration of the vehicle body becomes more intensively; under the couplingation action of vehicle and track, the matching between the weight and design frequencies of dynamic absorbers has to be considered; the design frequency threshold determines if dynamic absorbers reduce vibration and the optimal design frequency determines if dynamic absorbers have better vibration reduction effects. This study provided an important reference to evaluate and analyze vibration characteristics of urban rail vehicles with dynamic absorbers.
vehicle-track coupling; vertical vibration; dynamic absorber; vibration reduction; DVA vibration reduction index
国家自然科学基金(11472176);上海市自然科学基金(15ZR1419200);上海市研究生教育创新计划学位点引导布局与建设培育(13SC002)
2015-07-28 修改稿收到日期:2015-10-18
文永蓬 男,博士,副教授,1979年10月生
U260.331+.5;U270.1
A
10.13465/j.cnki.jvs.2016.21.009
