弱广义对角交叉积的表示范畴

陈笑缘， 贾 玲

(1. 浙江商业职业技术学院， 浙江 杭州 310053； 2. 鲁东大学 数学与统计科学学院， 山东 烟台 264025)



弱广义对角交叉积的表示范畴

陈笑缘1， 贾 玲2

(1. 浙江商业职业技术学院， 浙江 杭州 310053； 2. 鲁东大学 数学与统计科学学院， 山东 烟台 264025)

引入弱(H,A)-Yetter Drinfeld模和弱广义对角交叉积代数，证明了弱广义对角交叉积的表示范畴同构于弱(H,A)-Yetter Drinfeld模范畴.

弱Hopf代数；弱(H,A)-Yetter Drinfeld模；弱广义对角交叉积

BOHM等[1]引入的弱Hopf代数是Hopf代数重要的推广结构之一，随着Hopf代数理论体系的日臻完善，其在数学物理、量子群等领域的应用日渐广泛；Yetter-Drinfeld是Hopf代数理论中的重要结构，文献[2-3]引入的Yetter-Drinfeld数组进一步推广了结论，得到其上的模范畴同构于对角交叉积表示范畴；文献[4]讨论了Yetter-Drinfeld群模的表示范畴；文献[5]将Yetter-Drinfeld结构在弱Hopf群余代数环境下进行了重新构建.

本文讨论弱广义对角交叉积代数的表示范畴，推广了Hopf代数理论中的相应内容.关于弱Hopf代数的基本概念请参考文献[1，5-6].

定义1[1]H是域k上的弱Hopf代数.一个代数A被称为左H-余模代数指A是左H-余模且满足：

(1)∑(ab)(-1)⊗(ab)(0)=∑a(-1)b(-1)⊗a(0)b(0)；

类似地，右H-余模代数是一个k-代数A且是右H-余模,满足：

(3)∑(ab)[0]⊗(ab)[1]=∑a[0]b[0]⊗a[1]b[1]；

另外，如果A既是右H-余模代数又是左H-余模代数，且对任意a∈A，满足:

(5)∑a[0](-1)⊗a[0](0)⊗a[1]=∑a(-1)⊗a(0)[0]⊗a(0)[1]，

则称其为H-双余模代数.

注2 条件(2)和(4)可分别被下列式子替换：

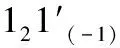
例1[1]H是k上的弱Hopf代数，则H是H-双余模代数可通过余乘法运算.

定义2 H是k上的弱Hopf代数.A是H-双余模代数.一个弱左-右-(H,A)-Yetter-Drinfeld模M指M是左A-模且是右H-模，且对任意a∈A,m∈M，满足以下等价条件之一:

(6)∑(a·m)[0]⊗(a·m)[1]=∑a[0](0)·m[0]⊗

a(-1)m[1]S-1(a[0](1))；

(7)∑a[0]·m[0]⊗a[1]·m[1]=∑(a(0)·m)[0]⊗

(a(0)·m)[1]a(-1).

用AYDH表示弱(H,A)-Yetter-Drinfeld模范畴.

引理1 H是k上的弱Hopf代数.A是H-双余模代数.则k-空间H*⊗A的如下乘法是结合的：

(α⊗a)(β⊗b)=∑α(a[0](-1)⇀βS-1(a[1]))⊗ a[0](0), b,α,β∈H*,a,b∈A.

证明 事实上，对任意α,β,γ∈H*,a,b,c∈A,[(α⊗a)(β⊗b)](γ⊗c)=∑α(a[0](-1)⇀βS-1(a[1]))×

(a[0](0)[0](-1)b[0](-1)⇀γS-1(a[0](0)[1]b[1]))⊗

S-1(a[1]2))(a[0](-1)2b[0](-1)⇀γS-1(a[1]1b[1]))⊗

a[0](0)b[0](0)c=∑α(a[0](-1)⇀

(b[0](-1)⇀βS-1(b[1]))⇀S-1(a[1]))⊗

a[0](0)b[0](0)c=(α⊗a)[(β⊗b)(γ⊗c)].

引理2 H是k上的弱Hopf代数.A是H-双余模代数，则形如α⊗a-(α⊗a)(ε⊗1)和α⊗a-(ε⊗1)(α⊗a),α∈H*,a∈A的元素所生成的k-空间I是H*⊗A的双边理想.

证明 实际上，对任意α,β∈H*,a,b∈A,

(α⊗a)(β⊗b)-(ε⊗1)(α⊗a)(β⊗b)=

∑α(α[0](-1)⇀βS-1(a[1]))⊗a[0](0)b-

(1[0](-1)⇀αS-1(1[1]))×

(1[0](0)[0](-1)⇀βS-1(1[0](0)[1]a[1]))⊗

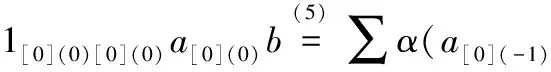
S-1(a[1]))⊗a[0](0)b-(1[0](-1)1⇀α

S-1(1[1]2))×(1[0](-1)2a[0](-1)⇀β

∑α(a[0](-1)⇀βS-1(a[1]))⊗

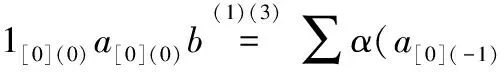
a[0](0)b-α(a[0](-1)⇀βS-1(a[1]))⊗a[0](0)b=0.

(β⊗b)(α⊗a)-(β⊗b)(ε⊗1)(α⊗a)=

∑β(b[0](-1)⇀αS-1(b[1]))⊗b[0](0)a-

β(b[0](-1)⇀εS-1(b[1]))×

(b[0](0)[0](-1)⇀αS-1(b[0](0)[1]))⊗

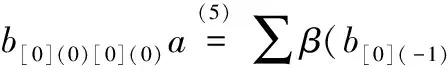
S-1(b[1]))⊗b[0](0)a-β(b[0](-1)1⇀εS-1(b[1]2))×

(b[0](-1)2⇀αS-1(b[1]1))⊗b[0](0)a=

∑β(b[0](-1)⇀αS-1(b[1]))⊗b[0](0)a-

β(b[0](-1)⇀(εα)S-1(b[1]))⊗b[0](0)a=0.

其他2个式子可类似证明.

注3 (1)若H是Hopf代数，则弱对角交叉积就是对角交叉积[3].

(2)令A=H，左右余模由余乘法给出，则弱广义对角交叉积就是通常意义下的弱量子偶D(H).

引理3 H是k上的弱Hopf代数,A是H-双余模代数.则有

证明 事实上，a,b∈A,α,β∈H*,

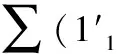
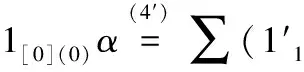
S-1(1(0)[1]2))(1(-1)2⇀εS-1(1(0)[1]1))⊗

1(0)[0]a=∑(1[0](-1)⇀αS-1(1[1]))⊗

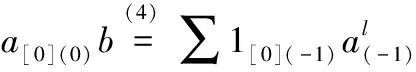
(1[0](0)[0](-1)⇀αS-1(1[0](0)[1]))⊗

∑(1[0](-1)1⇀αS-1(1[1]2))(1[0](-1)2⇀α

S-1(1[1]1))⊗1[0](0)=∑(1[0](-1)⇀(αβ)

证明 由式(9)，M显然是左A-模.只需证明其是右H-余模.因为对任意m∈M和α,β∈H*,

(idM⊗α⊗β)(m[0][0]⊗m[0][1]⊗m[1])=

mβ1(S-1(1[1]))β3(1[0](-1))=

(idM⊗α⊗β)(m[0]⊗m[1]1⊗m[1]2)=

β1(S-1(1[1]1))β3(1[0](-1)2)=

∑((1[0](-1)⇀(αβ)S-1(1[1]))1[0](0))·m=

证明 若M∈AYDH，则M自然是左H*-模，其作用为α*m=∑α(m[1])m[0].定义

∑α(a[1]m[1]S-1(a[0](-1)))a[0](0)m,

α∈H*,m∈M,a∈A.

首先，断言上述作用是合理的.事实上，对

α∈H*,m∈M,a∈A,

S-1(a[0](0)[0](-1)2))×

ε(S-1(a[1])a[0](0)[1]2m[1]2S-1(a[0](0)[0](-1)1)×

∑α(a[1]1m[1]1S-1(a[0](-1)2))×

ε(a[1]2m[1]2S-1(a[0](1)1))a[0]0m[0]×

S-1(a[0](-1))S-1(1[0](0)[0](-1))1[0](-1))1[0](0)[0](0)×

∑α(1[1]a[1]m[1]S-1(a[0](-1))×

S-1(1[0](-1)))1[0](0)a[0](0)·m[0]=

S-1(a[0](-1)3b[0](-1)2))×

β(S-1(a[1]3)a[1]2b[1]2m[1]2S-1(a[0](-1)2b[0](-1)1)×

a[0](-1)1)a[0](0)b[0](0)m[0]=

∑α(a[1]1b[1]1m[1]1S-1(a[0](-1)2b[0](-1)2))×

∑ε(m[1])m[0]=m.

∑f(α(a[1]m[1]S-1(a[0](-1)))a[0](0)·m)=

∑α(a[1]m[1]S-1(a[0](-1)))a[0](0)·f(m)=

∑(a[0](-1)2⇀α2S-1(a[1]1)a[0](0))∘mα1×

∑(1[0](-1)⇀αS-1(1[1])1[0](0)a)∘m=

[(1[0](-1)1⇀αS-1(1[1]2))(1[0](-1)2⇀εS-1(1[1]1))

1[0](0)a]∘m=∑(idM⊗α)((a·m)[0]⊗

(a·m)[1])∑(idM⊗α)(a[0]·m[0]⊗a[1]m[1])=

∑(a[0][0](-1)⇀α2S-1(a[0][1])

∑(1[0](-1)a(-1)⇀αS-1(1[1])1[0](0)a(0))∘m=

∑(1[0](-1)⇀α1S-1(1[1])

S-1(1[1]))(1[0](0)[0](-1)⇀εS-1(1[0](0)[1]))

1[0](0)[0](0)a(0)]∘mα2(a(-1))=∑(idM⊗α)×

((a(0)·m)[0]⊗(a(0)·m)[1]a(-1)).

[1] BOHM G, NILL F, SZLACHANYI K. Weak Hopf algebras (I): Integral theory and C*-structure[J]. J Algebra, 1999,221:385-438.

[2] CAENEPEEL S, MILITARU G, ZHU S. Frobenius and separable functors for generalized module categories and nonlinear equations [C]// Lecture Notes in Mathematics 1787. Berlin: Springer Verlag,2002.

[3] HAUSSER F, NILL F. Diagonal crossed products by duals of quasi-quantum groups[J]. Rev Math Phys, 2011,11(5):553-629.

[4] ZUNINO M. Yetter-Drinfeld modules for crossed structures[J]. J Pure Appl Algebra, 2004,193:313-343.

[5] JIA L. Yetter-Drinfeld π-modules over weak T-coalgebra[J]. Bull Braz Math Soc: New Series,2012,43(3):375-396.

[6] NIKSHYCH D. On the structure of weak Hopf algebras[J]. Adv Math, 2002,170(2):257-286.

CHEN Xiaoyuan1, JIA Ling2

(1.ZhejiangBusinessCollege,Hangzhou310053,China; 2.SchoolofMathematicsandStatisticsScience,LudongUniversity,Yantai264025,ShandongProvince,China)

The representation category of weak generalized diagonal crossed product. Journal of Zhejiang University(Science Edition), 2016,43(6):672-675

weak Hopf algebra; weak (H,A)-Yetter Drinfeld module; weak generalized diagonal cross product

2015-10-22.

山东省自然科学基金资助项目(ZR2012AL02).

陈笑缘(1963-)，ORCID:http://orcid.org/0000-0003-2898-9976,女,教授，主要从事代数研究.

10.3785/j.issn.1008-9497.2016.06.008

O 153.3

A

1008-9497(2016)06-672-04