基于改进切趾函数的Fourier光谱仪光谱复原效果的提高
2016-12-13江峰,盛文,蒋伟
江 峰,盛 文,蒋 伟
(空军预警学院,武汉 430019)
基于改进切趾函数的Fourier光谱仪光谱复原效果的提高
江 峰,盛 文,蒋 伟
(空军预警学院,武汉 430019)
为校正BlackmanHarris切趾函数在Fourier变换光谱仪切趾处理过程中主瓣宽度过宽的缺点,提出了一种改进的BlackmanHarris切趾函数。首先介绍了干涉图切趾的基本原理,然后增加可调参数m,引入Chebyshev函数对BlackmanHarris切趾函数进行改进,并通过幅频响应曲线对比了改进前后2种切趾函数的性能;最后利用Matlab仿真分析改进的切趾函数与几种典型函数的光谱复原效果。仿真结果表明,改进的切趾函数不仅在主瓣宽度特性上有所提高,而且旁瓣衰减可调节,工程使用更加灵活。
BlackmanHarris切趾函数;光谱仪;光谱复原
0 引 言
干涉型成像光谱仪经过多年的发展,已经广泛应用于环境科学、生物医学、航空航天、石油工业等十几类研究领域[1],它具有光谱测定范围宽、光谱分辨率高、扫描速度快、图谱合一、能量利用率高等众多优点[2]。各种型号的干涉型光谱仪发展非常迅速,以傅里叶变换红外光谱仪为例,每3~5年就有新型号的傅里叶变换红外光谱仪(FTIR)产生。但是干涉型成像光谱仪获取目标的干涉图像数据不能直接被利用,通常要经过复原处理成光谱数据以获取目标准确的光谱信息。随着干涉型光谱仪的不断发展,其光谱复原技术也在不断地发展。
对干涉图的切趾是光谱复原处理获取光谱图信息的重要环节,光谱复原的过程中,存在傅里叶变换,需要无限的积分区间,而实际干涉仪只能提供有限光程差的矛盾,这个矛盾会造成复原光谱存在旁瓣效应进而影响邻近的、微弱信号的测定,此时就需要将干涉图进行切趾处理,以消除或者减弱虚假的旁瓣,增强有用信号的被检测率[3-4]。张鹏、张志辉两人提出了一种阶跃切趾函数,用其处理过零单边干涉图时,可以减小数据误差,提高计算效率[5],但是这种处理方式没有给出对切趾函数的性质分析,并且函数过于简单;刘兵等人提出用Gaussian切趾技术对体光栅旁瓣进行抑制,减少光谱衍射损耗,但是文章在注重旁瓣抑制的同时,没有讨论Gaussian切趾技术对主瓣增宽效应、光谱分辨率下降的影响[6];李志刚等人使用四阶BlackmanHarris窗作为切趾函数对汞灯光谱干涉图进行了处理[7],但是BlackmanHarris窗作为一种具有强的旁瓣抑制能力的窗函数,其光谱分辨率指标同样不理想。因此,本文提出一种改进的Blackman-harris切趾函数,增加可调参数m,通过引入Chebyshev函数使得新的切趾函数兼顾了旁瓣抑制能力和主瓣宽度2个指标,同时新切趾函数简单易行,性能灵活,具有工程实用价值。
1 干涉图切趾原理
Fourier变换光谱仪干涉成像原理的基本公式为[8]:
(1)
(2)
式中:I(x)为光谱仪实际获取的干涉图;RT为复原光谱与实际光谱相差的倍数;B0(σ)为实际光谱;B(σ)为复原光谱;σ为光谱波数;x为干涉图光程差。
由式(1)、(2)可知,光谱仪探测到目标的干涉数据后,必须经过傅里叶变换才能得到最终的光谱数据,理论上要获取完整的光谱就要傅里叶变换的积分限为无穷大,但实际受限于光谱仪数据采集间隔、动静扫描距离以及计算机数据处理量等现实因素[9]。干涉图通常是理想干涉图与截断函数(矩形窗)的乘积,在频域上表现为实际光谱与Sinc函数的卷积:
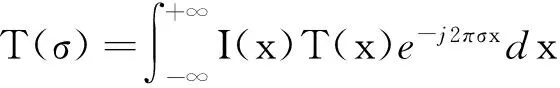
(3)
(4)
式(4)为矩形截断函数,其傅里叶变换T(σ)即为Sinc函数。Sinc函数为振荡收敛函数,其第一旁瓣强度达到主峰值的22%,强烈的正负旁瓣掩盖附近真实弱光谱信息的同时,也会带来虚假的光谱信号,因此必须对这些类似“脚趾”的旁瓣进行抑制,这个过程称为切趾。切趾处理是将实际测得的干涉图乘上一个渐变函数,达到降低旁瓣、缓和干涉图不连续程度的目的,另外,也可以通过将干涉图与切趾函数分别进行傅里叶变换后在频域上卷积的方法求得。切趾函数的选取一般要考虑以下原则[9]:
(1) 切趾函数的形式尽量简单,函数表达式便于计算;
(2) 切趾谱函数主瓣宽度尽量小,具有窄的半功率宽度;
(3) 切趾谱函数旁瓣尽量低,旁瓣收敛速度尽量快。
在实际应用中,上述3个条件往往不能全部满足,选择形式简单的切趾函数处理干涉图容易丢失有用的目标信号,选择强旁瓣抑制能力的切趾函数会造成主瓣宽度的增加,系统分辨率降低,因此要综合考虑切趾函数性质以及系统要求,选取合适的切趾函数。
2 改进的Blackman Harris切趾函数
在众多余弦组合窗中,Blackman-Harris窗函数具有极低的旁瓣峰值电平,能够很好地抑制频谱泄露,同时作为一种四项系数三阶余弦窗函数,切趾运算简单容易[10]。长度为N的Blackman-Harris函数时域表达式为[11-12]:
(5)
式中:0≤n≤N-1;a0=0.358 75;a1=0.488 29;a2=0.141 28;a3=0.011 68。
对其进行离散傅里叶变换可得频域表达式:
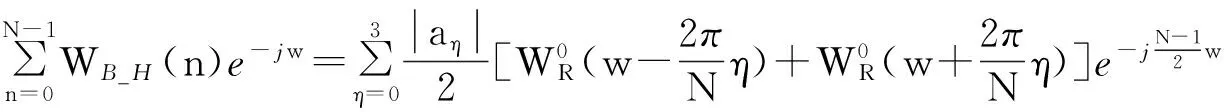
(6)
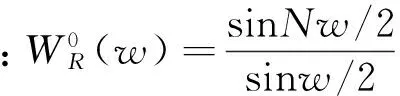
通过Matlab仿真,Blackman-Harris窗函数时域及归一化幅频响应如图1所示(N=128)。
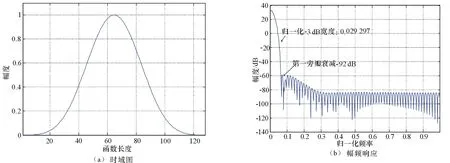
图1 Blackman-Harris函数时域及归一化幅频响应
由图1可以发现,Blackman-Harris切趾函数虽然有极低的旁瓣峰值电平,但是主瓣宽度较宽,当系统对分辨率要求较高时,Blackman-Harris函数显然不适用。为了更好地利用Blackman-Harris切趾函数的优点,对其改进显得十分有必要,通过查阅资料发现,在给定旁瓣高度下,Chebyshev切趾函数的主瓣宽度最小,满足切趾函数的最大振幅比准则[13],为此在原Blackman-Harris函数时域表达式的基础上,引入Chebyshev函数,增加了可调参数m,对Blackman-Harris切趾函数进行改进,令函数长度N=2M+1,则Chebyshev切趾函数的时域表达式为:
(7)
(8)
(9)
式中:γ为用分数表示的旁瓣与主瓣幅度的比值[14-15],通常可以根据实际情况设定。
式(9)为Chebyshev多项式。改进后的Blackman-Harris函数为:
(10)
式中:m(0≤m≤N)、γ均为可调参数,这使得改进后的Blackman-Harris切趾函数性能更加灵活。
改进后的Blackman-Harris切趾函数时域及归一化幅频响应如图2所示(N=128,m=2,20lgγ=-100dB)。
3 仿真与验证
比较图1(b)与图2(b)可以发现,在相同第一旁瓣衰减下,改进后的Blackman-Harris切趾函数主瓣宽度明显降低,为进一步验证改进后Blackman-Harris切趾函数性能,选取单色光干涉图(余弦波IR(x)=100×cos(2×π×4×x),采样频率100Hz,采样点数512点)进行切趾和光谱复原处理过程的模拟,仿真结果如图3所示。
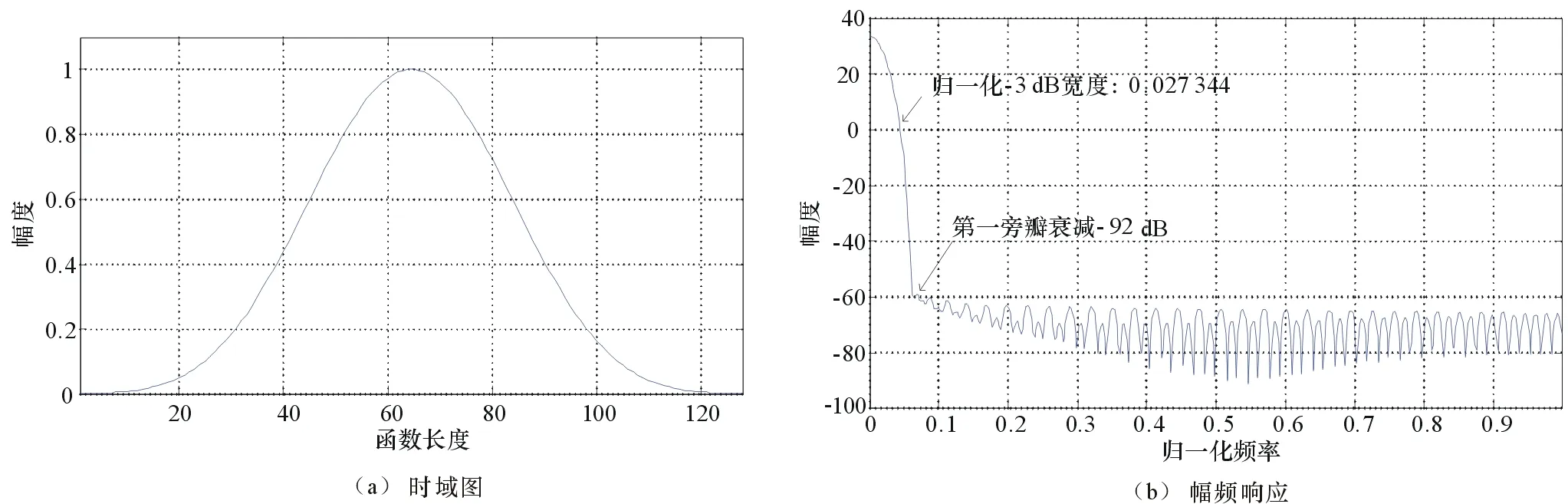
图2 改进的Blackman-Harris函数时域及归一化幅频响应
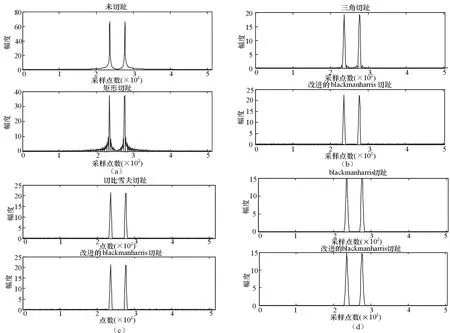
图3 改进的Blackman-Harris与几种典型切趾函数复原光谱仿真
图3中,(a)为矩形切趾复原光谱与原始光谱图的对比,可以看出,矩形切趾后旁瓣杂波明显增多,这与第1节中阐述的原理相符;(b)为改进后的Blackman-Harris切趾与三角切趾复原光谱对比(第一旁瓣衰减分别为20lgγ=-40dB、-27dB,N=200,m=2),在相同主瓣宽度下,前者旁瓣衰减优于三角切趾;(c)、(d)为改进后的Blackman-Harris切趾分别与Chebyshev切趾、原Blackman-Harris切趾复原光谱对比,图(c)中两者旁瓣衰减均为45dB,图(d)中两者旁瓣衰减均为92dB,通过调节参数m及γ,改进后的Blackman-Harris切趾函数不仅可以实现大多数切趾函数的功能,并且在主瓣宽度方面优于原Blackman-Harris切趾函数。
4 总结与展望
本文对Fourier变换光谱仪切趾处理过程进行了研究,提出了一种改进的Blackman-Harris切趾函数,提高了Fourier光谱仪光谱复原效果,该研究方法同样适用于其他切趾函数的处理。通过matlab仿真分析发现,改进后的Blackman-Harris切趾函数具有以下优点:(1)改进的Blackman-Harris切趾函数主瓣宽度得到了明显降低;(2)改进的Blackman-Harris切趾函数在相同主瓣宽度条件下,旁瓣性能优于三角切趾函数;(3)通过引入参数m及γ,改进的Blackman-Harris切趾函数第一旁瓣衰减可调,使用更加灵活,可实现大多数切趾函数的功能。
[1]RAFERTJB,SELLARRG,BLATTJH.MonolithicFouriertransformimagingspectrometer[J].JournalofAppliedOptics,1995,34(31):7228-7230.
[2] 孙德新,杨存武.高光通量短波红外静止干涉成像光谱仪研究[J].应用光学,2002,23(4):1-5.
[3] 李苏宁,朱日红,李建欣,等.傅里叶干涉成像光谱技术中的重构方法[J].应用光学,2009,30(2):268-272.
[4] 肖青,柳钦火,李小文,等.高分辨率机载遥感数据的交叉辐射影响及其校正[J].遥感学报,2005,9(6):3- 11.
[5] 张鹏,张志辉.一种新的过零单边干涉图切趾加权函数[J].光子学报,2012,41(7):878-881.
[6] 刘兵,李坚.Gaussian切趾体光栅在光谱合成中的应用研究[J].激光技术,2013,37(5):654-659.
[7] 李志刚,王淑荣,李福田.紫外傅里叶变换光谱仪干涉图数据处理[J].光谱学与光谱分析,2000,20(2):203- 205.
[8] 张士江.光谱重建中干涉图处理及其应用研究[D].合肥:安徽大学,2011.
[9] 杨琨.傅里叶变换红外光谱仪若干核心技术研究及其应用[D].武汉:武汉大学,2010.
[10]赵文春,马伟明,胡安.电机测试中谐波分析的高精度FFT算法[J].中国电机工程学报,2001,9(12):83- 87.
[11]刘海升,付志红,张淮清,等.基于Blackman-Harris相位差校正信号谐波分析方法[J].数据采集与处理,2011,26(4):468-472.
[12]ZHANGF,GENGZ,YUANW.ThealgorithmofinterpolationwindowedFFTforharmonicanalysisofelectricpowersystem[J].IEEETransactionsonPowerSystem,2001,16(2):160-164.
[13]《数学辞海》编辑委员会.数学辞海[M].北京:中国科学技术出版社,2002.
[14]OPPENHEIMAV,SCHAFERRW,BUCKJR. 离散时间信号处理[M].刘树棠,黄建国译.2版.西安:西安交通大学出版社,2001.
[15]MITRASK.数字信号处理——基于计算机的方法[M].孙洪译.3版.北京:电子工业出版社,2006.
TheAdvancementofSpectrumReconstructionEffectofFourierSpectrometerBasedonImprovedApodizationFunction
JIANGFeng,SHENGWen,JIANGWei
(AirForceEarlyWarningAcademy,Wuhan430019,China)
InordertorectifytheshortcomingsoflargemainlobewidthofBlackmanHarrisapodizationfunctioninapodizationprocessingofFouriertransformspectrometer,animprovedBlackmanHarrisapodizationfunctionisputforward.Firstlythispaperintroducesthebasicprincipleofapodizedinterferogram,andthenaddsatunableparameterm,introducesChebyshevfunctiontoimproveBlackmanHarrisfunction,andcomparestheperformancesoftwoapodizationfunctionsbeforeandafterimprovementthroughamplitude-frequencyresponsecurves,finallyusesMatlabtosimulateandanalyzethespectrumreconstructioneffectofimprovedapodizationfunctionandseveraltypicalapodizationfuncation.Thesimulationresultsshow:fortheimprovedapodizationfunction,notonlythecharacteristicsofmainlobewidthisenhanced,butalsothesidelobeattenuarioncanbeadjusted;sothefunctionismoreflexibleinengineeringapplication.
BlackmanHarrisapodizationfunction;spectrometer;spectrumreconstruction
2016-04-05
国家自然科学基金,项目编号:61271451
TH
A
CN32-1413(2016)05-0077-05
10.16426/j.cnki.jcdzdk.2016.05.020
