小学数学课堂结构立序思考
2016-12-12荀步章
荀步章


任何学科的内核是其结构,而不是具体的技术细节;尽管结构的本质是简单的,但其存在形态却可以是复杂的;任何学科,都是以结构为中心的符号形式系统。(布鲁纳)数学课程结构严密,数学课堂的教学结构更具普适性。如何体现认知主义的教育思想,使课堂符合学生的认知规律,促进学生的思维发展呢?
一、立知识发展之序,助学生思维生长
学科的内核是结构,课堂与学科结构保持一致性,才能遵循学生思考问题的本质。追求知识与课堂发展的顺序性,不囿于具体的技术细节,帮助学生思维更好地生长。以下选取苏教版教材“确定位置”教学内容,分析教材编排与课堂生成追求的结构。
1. 承前:用数对确定位置的起点。学生的已有经验是用一个数确定位置,一上教材第14页,老爷爷和小朋友排队买票,他们排成了一排,以窗口为“参考物”,老爷爷排第一,戴帽孩子排第二。这些内容,学生有相应的生活经验,教学时要激活他们的生活经验,用数学表述的方式描述,让他们学会在一条线上说清“第几”。
2. 需求:用数对确定位置的方法。一年级学习用“第几”确定位置后,五下教材第15页,学习用两个数确定位置。例题选取学生班级座位图,从熟悉的情境出发,问:“小军坐在哪里?”学生回答时出现几种不同说法:“小军坐在第4组第3个”“小军坐在第3排第4个”等。由于说法不一致,产生统一说法的必要性:数学中的常用规定是,“竖排叫做列,横排叫做行。确定第几列一般从左往右数,确定第几行一般从前往后数”。把学生座位图抽象成点图,小军坐在第4列第3行,让学生创造如何表示他的位置,并说一说为什么这样表示。
3. 突破:用数对确定位置的超越。学会用数对确定位置后,学生需进行一些必要的强化练习。观察常规的课堂练习,归纳出来都是找数对与位置的对应关系,且仅限整数。为了防止学生出现思维定势,需要设计一些挑战性习题。如图1,已知A点用数对(3,2)表示,估计B、C两点分别用什么数对表示?让学生充分猜想,并说出猜的根据,然后出示图2。点B用数对(5,3)表示,部分学生能够猜出来。但C点全班学生都没有猜出来,因为它并不是我们通常所说的整数,而用小数表示数对,可以用(6?郾5,3?郾5)表示,学生又提出可不可以用分数表示?引发学生用不同方法表示数对的兴趣,并与后续的学习有效对接。
4. 延伸:线→面→体,用数对确定位置升华。学生掌握了用数对确定位置后,还不能停留于此,拓展学生的思维十分必要。帮助学生梳理,在一条线上,如何表示(图3),从左向右数第4个,从右往左数第3个。由线到面,一排一排出示(图4),红色涂一点,如何表示?学生很快得到用数对表示为(4,2),唯一表示,简洁方便。再由面到体,一层一层出示(图5),共三层,在最上层找一个点涂上红色,用什么方法表示呢?有学生提出用三个数来表示,思维得到了生长。
二、立认知需求之序,促学生思维成长
学习结构,就是要学习事物是如何关联的。(布鲁纳)一节课的时间虽短,但其结构存在形态却可以是多样的。高等数学与幼儿数学在结构上是一致的,但存在形态上具有很大差别。因此,在结构(不是具体知识形态的)意义上,任何学科都可以按照学生智育上发展的规律有效地对他们展开教学。例如低年级的“求差问题”,教师出示图6问学生:“苹果比梨多几个?”学生回答:“多2个。”“为什么?”教师接着问。学生回答:“就是多2个。”
教者设计意图是苹果和梨是一一对应的,右边多出来的两个,就是苹果比梨多的两个。然而学生心里怎样想?一眼就能看出多2个,这还要问吗?教材是静态文本的“终结”呈现,过程的设计需要教师来创造。因此,设计教学结构时需要用“倒序”的策略。
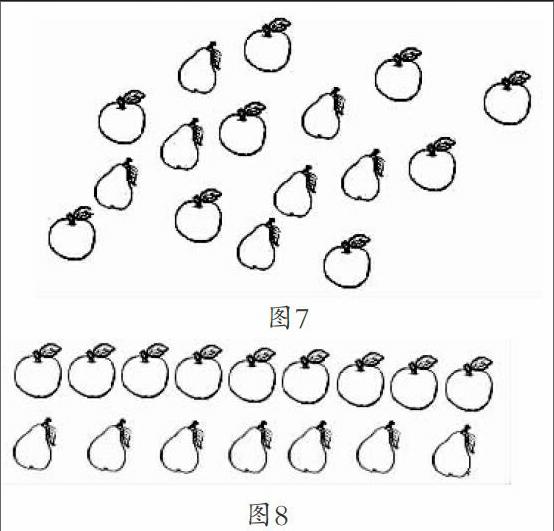
师(出示图7):苹果多,还是梨多?
生(慢慢地数):苹果有9个,梨有7个,苹果比梨多2个。
师:数的感觉怎样?
生:麻烦。
师:有好办法吗?让人一眼就看出来,苹果比梨多几个?
生:把苹果和梨排成一排。
师:好,我们就来排一排。
师:看一看,苹果和梨一样多?
生:不对呀,苹果比梨多2个呢。
师:看起来一样呀!
生:我们要把苹果和梨子对齐着放。
教师再出示图6。
师:这样放吗?为什么要这样放呢?
生:因为这样放,苹果和梨一个一个对齐了,一下子就看出苹果比梨子多2个。
教材中静态的文字和图片,让学生建构怎样的顺序,课堂要呈现怎样的结构,让学生经历怎样的思维,这些都值得每一位数学教师细细思考。这里采用“倒序”的方式,先“立序”后“编材”,帮学生建立“一一对应”的思想,从“无序”到“有序”,从“有序”到“一一对应”,层层螺旋上升,而不是“强硬”塞给学生。课堂上先呈现给学生一组杂乱的苹果和梨的图,让他们通过数一数的方法解决问题,感受其中的繁琐,产生摆成一排比一比的心理需求。接着,学生按要求把苹果和梨排成一排,但不是一个对着一个,两种水果两端对齐,感觉到还不够“工整”,产生“一一对应”的需求。学生在这一过程中,慢慢感悟到数学思想方法,积累一些数学活动经验,发展数学思维能力。
三、立路径验证之序,提学生思维快长
布鲁纳强调要重视儿童高级思维能力的开发,如顿悟与直觉思维等,它们在科学发现中起着重要的作用,应得到充分的关注。在“乘法交换律和结合律”教学时,学生循不同路径去思考,直觉感知去发现,都是课堂教学中的重要资源。学生通过自学教材了解乘法交换律用字母表示为“a×b=b×a”,教师采用展示学生思维的方式呈现课堂结构。
师:你们有方法证明吗?
生:可以举例子。
生:1×2=2×1,2×3=3×2,5×6=6×5。
师:例子举得完?有多少个?
生:举不完,有无数个。
师:猜想出来的规律,我们需要通过不同路径来验证。刚才,同学们举了很多例子,还有办法吗?其实,我们很早就明白这个道理了,看图9,停车场停12辆汽车,如何计算呢?
生:可以用4×3=12(辆),也可以用3×4=12(辆)。
师:我们可以根据这幅图,验证乘法交换律,一排停a辆车,一共有b排,停车场的车辆一共有多少辆?可以用(a×b)辆,也可以用(b×a)辆,结果应该是一样的。
乘法交换律教学一般是从教学情境出发,一道算式引发思考,学生举例发现交换律的规律。而上述片段则从规律本身出发,提出猜想:这个乘法交换律对吗?如何证明?通过大量举例发现规律的确定性,却只是不完全归纳法。验证规律还可以通过不同路径,从常见的情境图出发,采用二维图不同计算方法再次验证乘法交换律,使学生深刻感受到,规律是客观存在的,并且是被经常运用的。由此推及乘法结合律的教学。
师:乘法还有什么运算律?
生:乘法结合律(a×b)×c=a×(b×c)。
师:你们有方法证明吗?例子举得完吗?有多少个?
生:举不完,有无数个。
师:有办法验证乘法结合律吗?哪种图能说明呢?同学们在三年级学习乘法时做过一道题(图10),一共有多少箱苹果,怎么列式?
生:5×3×4。
师:先求什么?再求什么?
生:先求第一排有15箱,再求4排一共多少箱。
生:5×4×3,先求第一层有20箱,再求3层一共多少箱。
生:还可以竖着求,4×3×5,先求一列12箱,再求5列一共多少箱。
师:其实,同学们在列式的过程中,就存在着乘法结合律,(5×3)×4=5×(3×4)。
验证乘法结合律,学生会从乘法交换律中迁移,通过大量举例感受并验证乘法结合律的存在性。教师结合学生的生活阅历,运用教材原题,让学生进一步体验从不同角度观察,发现不同的列式方法,并及时呈现不同算式,联系生活意义,发现我们经常无意识地使用着乘法结合律。这里,教师通过停车场的车辆图,从横、竖不同方向观察,培养学生有序观察,比较思考中验证发现乘法交换律。从堆放苹果箱的三维立体图中,采用数形结合的方法,从不同角度整体上观察,学生从已有认知结构中提取经验,思考不同摆放形成的不同列式,数学思维在不同层次中有序发展,积累数学活动经验,提升数学素养。
小学数学课堂以结构为中心、知识信息为纽带、运算符号为系统,从关注情境、获取信息到理清情节,从把握关键到抽象概括,从建立模型到解决问题,从拓展模型到检验结果,回归原始问题的答案,这种数学结构的魅力是推动学科发展的有效动力。通过学生参与数学活动,使他们切身体会到数学并非只应用于数学自身,完全可以解决现实生活中和其他学科中的问题,数学教育的重心要放在培养学生的核心素养上。
(作者单位:江苏省宝应县实验小学)
