Solution of Liouville’s Equation for Uncertainty Characterization of the Main Problem in Satellite Theory1,2

Ryan Weisman,Manoranjan Majjiand Kyle T.Alfriend

Solution of Liouville’s Equation for Uncertainty Characterization of the Main Problem in Satellite Theory1,2

Ryan Weisman3,Manoranjan Majji4and Kyle T.Alfriend5

This paper presents a closed form solution to Liouville’s equation governing the evolution of the probability density function associated with the motion of a body in a central force field and subject to J2.It is shown that the application of transformation of variables formula for mapping uncertainties is equivalent to the method of characteristics for computing the time evolution of the probability density function that forms the solution of the Liouville’s partial differential equation.The insights derived from the nature of the solution to Liouville’s equation are used to reduce the dimensionality of uncertainties in orbital element space.It is demonstrated that the uncertainty propagation is fastest in the semi-major axis and the mean anomaly phase sub-space.The results obtained for uncertainty propagation for the two body problem are applied to investigate the uncertainty propagation in the presence of the J2perturbation using a combination of osculating and mean element perturbation theory.Analytical orbital uncertainty propagation calculations are validated using Monte-Carlo results for several representative orbits.

Astrodynamics,Uncertainty Quantification.

1 Introduction

Owing to the proliferation of orbital debris[Kessler and Cour-Palais(1978)]and imposing threat of Earth impacting asteroids[Junkins,Singla,Mortari,Bottke,and Durda(2005)],uncertainty characterization and propagation research has occupied a center stage in modern space system design applications.Traditional methods of linear covariance analysis and associated sequential orbit estimation strategies are of limited utility when the propagation times between measurements of the space objects grows large.Nonlinearity of astrodynamics problems makes the evolution of the probability density function that governs the uncertainty of the state vector non Gaussian in nature.This non-Gaussian[Junkins,Akella,and Alfriend(1996)]evolution of uncertainty cannot be captured faithfully using linearized models.

The Fokker-Planck equation[Risken(1996)]dictates the evolution of the probability density function(PDF)associated with the state vector of a dynamical system that is a Markov process.Recently,researchers have developed efficient methods to solve the Fokker-Planck equation for high dimensional problems.Park and Scheeres (2006) developed the high order state transition tensor approach for propagation of uncertainties in orbital mechanics problems.Kumar,Chakravorty,Singla,and Junkins(2009)and Kumar,Chakravorty,and Junkins(2010)provided finite element formulations to solve the Fokker-Planck equation for determination of the transient and stationary probability density function solutions.Terejanu,Singla,Singh,and Scott(2008)provide a computational method to propagate uncertainty through nonlinear systems of high dimensionality using Gaussian mixture models.For astrodynamics problems,the general nonlinear motion models are well understood but sparse observations and incomplete state information and low precision require accurate uncertainty quantification.The presence of high fidelity dynamics models reduces the need to use high levels of process noise in the propagation equation to capture the model uncertainties and appropriate time-scale analysis allows for identification of when nonconservative forces begin to significantly contribute to motion.Therefore,the diffusion term of the Fokker-Planck equation can be neglected in the uncertainty propagation calculations for astrodynamics problems where it has been shown when and how nonconservative forces start to manifest[Awad,Narang-Siddarth,and Weisman(2016)].The Fokker-Planck equation without the diffusion term becomes Liouville’s equation that governs the evolution of the probability density function between two time steps of interest.To this end,Halder and Bhattacharya(2011)apply the method of characteristics to solve Liouville’s equation for computing the evolution of the probability density function in atmospheric re-entry problems.Fujimoto,Scheeres,and Alfriend(2012)use the state transition tensor approach to provide an expression for the probability density function at an arbitrary time instant.Analytical expressions for the state transition tensors are used by Fujimoto,Scheeres,and Alfriend(2012)and Majji,Junkins,and Turner(2008a)provide a set of partials required to compute the state transition tensors.The evolution equations for high order statistical moments are derived as a set of tensor differential equations by Majji,Junkins,and Turner(2010),providing an alternative approach for uncertainty propagation in terms of moments rather than the probability density function.In this work,state transition tensors are avoided by use of mathematical perturbation theory used to derive the mean orbital elements[Brouwer(1959)].

Liouville’s Equation is an important partial differential equation in statistical physics that describes the time evolution of the phase space distribution function[Gibbs(1902)].It originally appears in the classical and statistical mechanics asserting the conservation of the probability density function in the phase space for a conservative dynamical system.The equation is a set of quasi-linear partial differential equations that govern the time evolution of the PDF of the system states subject to a Markov process.For a conservative dynamical system,the partial differential equation specializes the evolution of the probability density in time to that of a system being governed by a state-transition matrix formulation.Even further,the dimensionality of the conservatively perturbed system can be reduced if any momenta variables for the system are able to be shown to be constant in time through use of Hamilton’s equations.

In addition to covariance intersection and threat assessment,uncertainty propagation methods are useful for state estimation.Park and Scheeres(2006)provide an estimation framework based on state transition tensors,where the propagated higher-order moments are used to compute an improved Kalman gain matrix.However,with each set of measurements,only the state and the covariance are updated,while the higher-order moments are not updated in this filter.Majji,Junkins,and Turner(2010)and Majji,Junkins,and Turner(2008b)extend this approach to propagate and update the high order moments to realize a high order extended Kalman filter.Efficient and accurate probability density function evolution(in contrast to the high order statistical moment propagation)calculations using Gaussian mixture models enabled Terejanu,Singla,Singh,and Scott(2011)to develop an implementation of a Bayesian filtering approach for nonlinear dynamic systems.For problems in astrodynamics and where the time-scale analysis permits,further computational efficiency is obtained for filtering,prediction,and tracking applications by neglecting the diffusion term in the Fokker-Planck equation that governs the time evolution.

In most problems of interest however,the analysts do not have direct access to the state variables due to incomplete state observations,sparse observations,and noisy observations.In such cases,estimation techniques are used to obtain initial condition estimates such that the trajectories of plant models of interest can be computed using these estimates.Usually the presence of noise prevents the analyst from estimating the system parameters(such as the initial conditions)exactly.Thus the uncertainty associated with the system parameters manifests itself and evolves in time in many problems of interest in astrodynamics.

This paper aims at studying the uncertainty propagation in orbital mechanics problems by making use of Liouville’s equation and mathematical perturbation theory.Results are shown for both Keplerian motion and the Main Problem in Satellite Theory(J2zonal perturbed two-body motion)[Deprit(1969)].Considerations about the choice of coordinates in astrodynamics are discussed that make the solution of this quasi-linear partial differential equation.

The rest of this paper proceeds as follows:Section 2 introduces Hamiltonian mechanics and nomenclature,Section 3 details Liouville’s equation along with the Method of Characteristics and the transformation of variables approaches to its solution,Section 4 provides the solution to Liouville’s equation for Two-Body motion with Keplerian and Delaunay variables,Section 5 shows the results of uncertainty propagation with Two-Body motion,Section 6 introduces Brouwer-Lyddane theory for derivation of mean orbital elements along with Lie Series and the first-order transformation between mean and osculating elements,and Section 7 provides numerical results for uncertainty propagation in the main problem of satellite theory.

2 Hamiltonian Mechanics

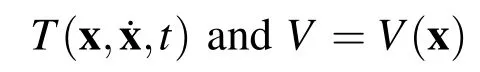
Legendre’s transformation[Goldstein,Poole,and Safko(2002)]defines the Hamiltonian function for the dynamical system in terms of the Lagrangian as

for all i=1,...,n.

Hamilton’s canonical equations have an inextricable relationship with the choice of generalized coordinates and the resulting momenta,as defined by the Legendre transformation.Depending on the choice of the coordinates,the description of the time evolution of the phase volume gets tremendously simplified,with significant impact on the uncertainty propagation,as described by Liouville’s theorem discussed in the next section[Goldstein,Poole,and Safko(2002)].The systematic pursuit of such coordinate choices is contingent upon a transformation known as the generating function that is obtained by the solution of the Hamilton Jacobi partial differential equation.

3 Liouville’s Equation

This section follows the discussion of our previous work[Majji,Weisman,and Alfriend(2012)]and is repeated here for completeness instead of cross-referencing.Consider the differential equation governing the evolution of the state from one time step to another to be given by

with initial conditions z(t0)=z0,where z∈Rn.Whenz0is a deterministic quantity,the solution of the dynamical system given in Eq.6 is guaranteed to exist and can be computed by using standard techniques.For a stochastic z0,the quasi-linear partial differential equation governing the time evolution of the probability density function,u(z,t)is given by

with a boundary(at initial condition)density function given by u(z,t)=u(z0,t0).Stated in this manner,z denotes the state vector,n is the number of states in the dynamical system,and the functional,fi,is given by Eqs.4 and 5.For a conservative dynamical system,the structure of the system of differential equations specializes the evolution of the density function in time.This can be shown from first principles by using the nature of the differential equations for a Hamiltonian dynamical system.Using the differential equations,we can write

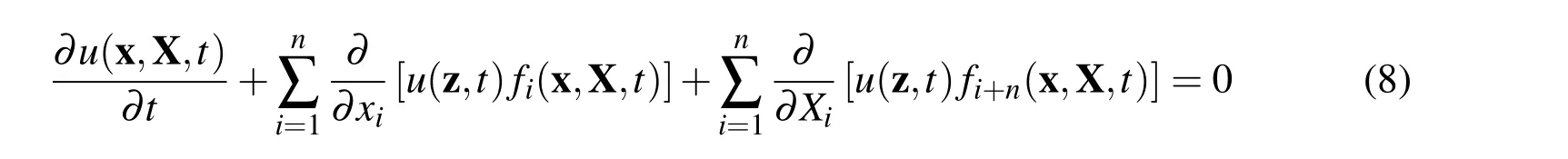
For the special case of the dynamical system described using Hamilton’s canonical equations,we make use of the fact that

and substitute these equations in the partial differential equation in Eq.8 to obtain Eq.9.The resulting partial differential equation using Einstein notation with i ranging over the number of degrees-of-freedom of the system is then

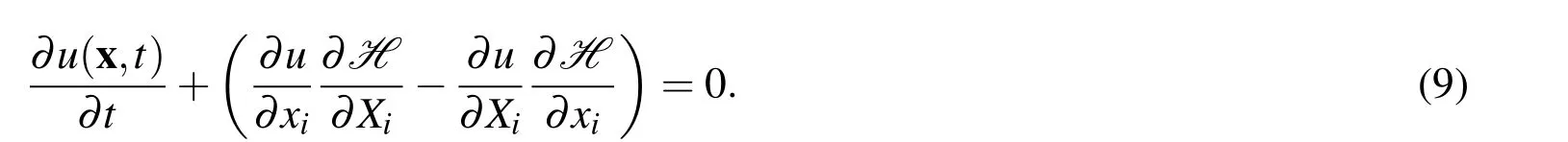
Since the second term in the equation is the Poisson bracket[Schaub and Junkins(2010);Battin(1990)],Eq.9 can be expressed using the Poisson bracket notation(.;.),resulting in

3.1 Methods of Solution:Method of Characteristics

In the theory of partial differential equations,Liouville’s equation belongs to a class of first order partial differential equation(PDE)in several variables that are quasilinear in nature[Evans(1998)].From the theory of partial differential equations,it is possible to use the method of characteristics[Halder and Bhattacharya(2011)]for solution of Liouville’s equation to compute the transformation of uncertainty between two time steps of a general dynamical system,not necessarily conservative in nature.

The method of characteristics transforms the solution process of a PDE in n dimensions into a set of ordinary differential equations(2n+1 in number).Once the characteristic curves are determined from the solution of the ordinary differential equations of interest,they are used to symbolically map the boundary condition into the solution at the current time.In essence,the existence of a smooth path between the boundary curve(density function)and the density function at an arbitrary instant of time is assumed.This path is called the characteristic curve.However,it is in general impossible to solve these problems analytically,because for most problems of interest,the characteristic curves turn out to be the solutions of the(usually)nonlinear equations of motion of the dynamical system considered.

3.2 Methods of Solution:Change of Variables

Using the method of characteristics theory,whether or not the solution of the dynamical system is the characteristic curve mapping the boundary density function to the current functional can be assessed.If so,they are related by smooth functional relationships.Therefore a smooth mapping should exist between u(x(t0),t0)andthe solution at current time u(x(t),t).Under these conditions,the change of variables formula can be applied using the fact that u(x(t0),t0)=u(x(t0)(x(t)),t0(t)).For notational convenience,denoting the boundary curve by u(x(t0),t0)=u0(x(t0),t0),results in sayingthat u0(x(t0),t0)=u0(u(x(t),t))!The example provided by Halder and Bhattacharya(2011)is used to demonstrate the solution process.Their example 1 involves the scalar dynamical system

with a symbolic initial condition x(0)=x0.For the Liouville’s equation an initial probability density function ϕ0(x0)is assumed to be given.The solution of this nonlinear differential equation can be written as

This relationship is invertible and can be written as

To provide a straightforward solution,consider the transformation of variables formula.Let η =g(ζ )be an invertible,continuously differentiable mapping,with a differentiable inverse,ζ =g−1(η ).If the probability density function of the variable ζ denoted by pζ(ζ )is known,then the probability density function of the transformed variable η is given by

The existence and differentiability of the functional relationship and an inverse between the current state x(t),η in Eq.14,and the initial state x0,ζ with the inverse functional relationship in Eq. 13. Straightforward application of the formula in Eq.14 gives the probability density function ϕ(x)in terms of the initial density function ϕ0(x0)given as

This solution can be verified to be the same solution obtained by Halder and B-hattacharya(2011).This shows the theory behind the method of characteristics is implicit in the application of the change of variables formula application.This is an important tool for mapping uncertainties in time,in addition to the other applications outlined in recent work for orbit filtering and propagation[Majji,Junkins,and Turner(2011);Weisman,Majji,and Alfriend(2011);Majji,Weisman,and Alfriend(2012)],attitude filtering and system parameter identification[Weisman(2012);Weisman,Majji,and Alfriend(2014a)],and orbit determination and filtering using different state variable representations[Weisman and Jah(2014);Weisman,Majji,and Alfriend(2014b)].

4 Solution of the Liouville’s Equation for Keplerian Motion

Keplerian motion is one of the most important nonlinear problems that analysts have been able to develop clear understanding about due to existence of a closed form solution[Battin(1990)].The two body problem is one of the most elegant solutions for a set of nonlinear differential equations and forms an important body of useful mathematical literature with widely applicable results.However,the transformation of uncertainty and its propagation for filtering and collision assessment have been important challenges for astrodynamists even in the ideal situation of the two body problem.Junkins(1997),Junkins and Singla(2003),and Junkins,Akella,and Alfriend(1996)have argued that the choice of coordinates is an important consideration in computation of meaningful uncertainties of orbital dynamics models.Recent investigations by Izzo(2006)use delta functions to give several useful probability density function formulae for problems of interest in astrodynamics starting from full state information.However,the lingering question about the choice of coordinates and the ease of solution methods has not been satisfactorily answered in the astronautics community.In this vein,let us consider the solution of the Liouville’s equation in three different coordinate systems.

4.1 Cartesian Coordinates

While the Cartesian coordinates are canonical for the two body problem,the solution of the Liouville’s equation is an insurmountable analytical task in these coordinates.This is because the Cartesian version of the two body problem shows up in computing the characteristic curves(or equivalently in the initial to current state mapping approach using the change of variables formula).While numerical solutions are possible,as has been presented by Halder and Bhattacharya(2011),no new insight is gained other than number crunching and hyper-histograms.

4.2 Solution in Kepler Elements

We now consider the Kepler elements with the mean anomaly as the time variable.The time evolution equations for this set can be directly written in the solution form as

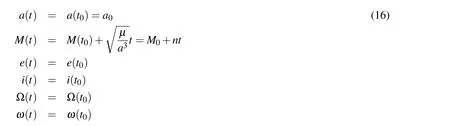
where t is an arbitrary time,t0is the epoch time at which the mean anomaly attains the value M0andµis the gravitational parameter.Clearly the only equation with linear time evolution is the mean anomaly M(t).Given the mapping of Eq.16,it is seen that although nonlinear,the inversion relationships between the elements at initial and current time are rather trivial(including M(t)).The determinant of the inverse Jacobian required for the transformation is unity.Thus if we are given an initial joint density function in-terms of the classical Kepler elements,

we can immediately construct the probability density function at the current time and give a symbolic expression for it as

While the expression for the probability density function at an arbitrary time instant is readily obtained for exponential family of probability density functions,Gaussian sum or other approximations for domain mapping need to be invoked in general.Since the expression for the transformed density is available for all time,its evaluation incurs trivial cost,making the process quite efficient when compared to Monte-Carlo based methods.If the initial density function in the orbital element space is given to be a Gaussian distribution with a mean vector given by[µa0,µM0,µe0,µi0,µΩ0,µω0]Tand a variance value given by σa0,σM0,σe0,σi0,σΩ0for each variable with zero cross covariance values(covariance matrix is diagonal),

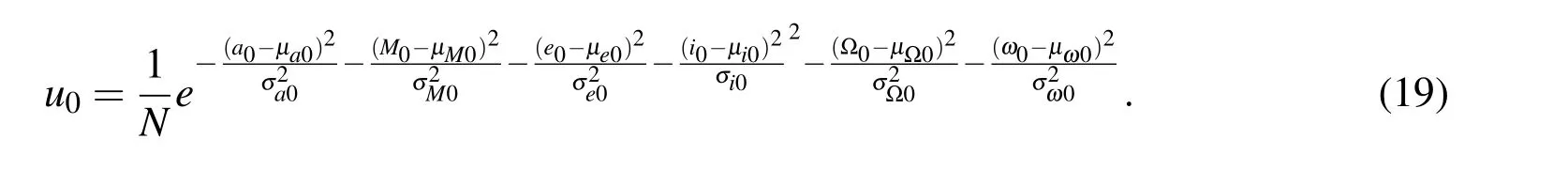
where N=8π3σa0σM0σe0σi0σΩ0is the normalization constant for the PDF.For the actual PDF forms resulting from radar or angles-only initial orbit determination and filtering see Weisman,Majji,and Alfriend(2014b)and Weisman and Jah(2014).Using Eq.18,we can now write an expression for the PDF at an arbitrary instant of time t＞t0given by

In the analytical expression for the PDF at an arbitrary time instant,t,the dominant evolution occurs between the mean anomaly M and the semi major axis a random variables because of the Kepler laws of planetary motion for the two body problem.The orientation parameter uncertainties remain unaffected and their corresponding uncertainties remain stationary in time.This is an important result of the analytical solution of the Liouville’s equation.It enables the analyst to compute uncertainties in the reduced phase space(namely a,M variables).

4.3 Solution in Delaunay Elements

A similar solution can be obtained in the Delaunay variables that are canonical in nature.The Delaunay variables are defined as

where new symbols l,g,h have been introduced to denote the mean anomaly M,argument of the periapsis ω and longitude of the ascending node,Ω to emphasize the canonical nature of the Delaunay elements with respect to their momenta(L,G,H).Similar to the Kepler elements,the probability density function at any time can be written as a function of the initial probability density function using the transformation of variables formula.Evolution of uncertainty in the Delaunay element space can be accomplished along the same lines of the Kepler elements by using the analytical expression for the flow of the dynamical system.However,the dimensionality reduction available in the Kepler elements does not lend itself to the Delaunay space since the variables G,H are functions of the variable L.Accordingly,the variables L,G,H co-vary with the mean anomaly l while the uncertainties with respect to the two orientation variables g,h remain stationary throughout the motion of the dynamical system.We now apply the solution to a representative problem and compare the evolution of the PDF with histograms of trajectory simulations propagated using a Monte-Carlo approach.

5 Numerical Example:Uncertainty Propagation Through Two Body Dynamics

In uncertainty propagation problems involving three or more dimensions,it is customary to plot either conditional density slices of the PDF or to show marginal density function contours.However,owing to the special nature of the Kepler element space,we observe that the joint density of the Mean anomaly and the semi-major axis are the pair of states that covary widely.The other state variables maintain constant dispersion characteristics with each other,shown by Eqs.16 and 20,there is no mixing of the probability density fluid with other variables in the Kepler element space.This unique property of the Kepler elements enables a significant dimensionality reduction for analysis and design.This is lost when another angle variable is used.For example,using the true anomaly instead of the mean anomaly makes the evolution of uncertainties jointly correlated with the eccentricity and semi-major axis together.In addition to this,we make use of the initial mean anomaly which varies more slowly when compared to its alternatives(true and eccentric anomalies).

The initial density function according to the assumptions is contoured in Fig.1.The use of a large standard deviation for the semi-major axis implies that a fraction of the uncertain phase volume goes through the Earth over the course of its orbit,the unusually large uncertainty in the semi-major axis is used purely for analysis purposes to demonstrate the utility of the approach.This density upon integration to the next time instant t=0.25 TU evolves into the density function as plotted in Fig.2.The intermediate time step is shown to demonstrate the fast evolution of the conditional joint density between the semi major axis and mean anomaly of interest.Subsequent evolution at t=0.50 TU is plotted in Fig.3 to show the speed of uncertainty evolution.

To validate the results of the analytical solution,we make use of Monte-Carlo simulations carried out by generating random initial mean anomaly and semi major axis value with specified statistics and propagating the state vector to t=0.5TU.There were 1×106initial condition samples with two-body equations of motion used to propagate to the final time for the Monte Carlo solution and 2.5×105were used for the analytic representation.The semi-major axis and mean anomaly space was subsequently discretized in to a space of 750x750 bins to compute a histogram of the final conditions attained by the propagated initial conditions.Upon normalization,this histogram represents an approximation of the(conditional)joint density of the mean anomaly and the semi major axis.The approximate PDF obtainedfrom the Monte-Carlo simulations is plotted in Fig.4.The jagged edges on the contours of the approximate density function are caused by the randomized initial condition generation process.The generated initial condition samples cannot guarantee a uniform state distribution at final time in all the bins of interest.Therefore,the histogram is noisy because of these binning artifacts being carried over to the contour plot.With the exception of these artifacts,it can be seen clearly that the approximate density function agrees to within plotting accuracy with the analytical solution that is computed almost instantaneously in Fig.3.For evolution of uncertainty over 3 orbital periods,～32 TU,Fig.5 and Fig.6 display the Monte Carlo and analytic transformation results respectively.For the orbital period results,the number of Monte Carlo bins was increased to 3750 by 3750.The modulus of mean anomaly is not performed to keep the shape intact for presentation,if the modulus were performed the area of highest uncertainty(semi-major axis range of 1.3 to 1.6 Earth Radii)would encompass the entire range of Mean Anomaly.After 1 orbital period the area of highest uncertainty spans 2 radians in Mean Anomaly space.The Monte Carlo reconstructed PDFs,have fewer points in the tail region which is accentuated by the longer propagation times.The relatively minor shape disagreement between the Monte Carlo generated equal probability contours of Fig.5 and the solution to Liouville equation in Fig.6 is attributed to this fundamental property of MC simulations.Note that,this feature of accurate characterization of contours of low probability is very useful in conjunction analysis.

Table 1:Initial Statistics of the Keplerian Elements for Two Body Uncertainty Propagation

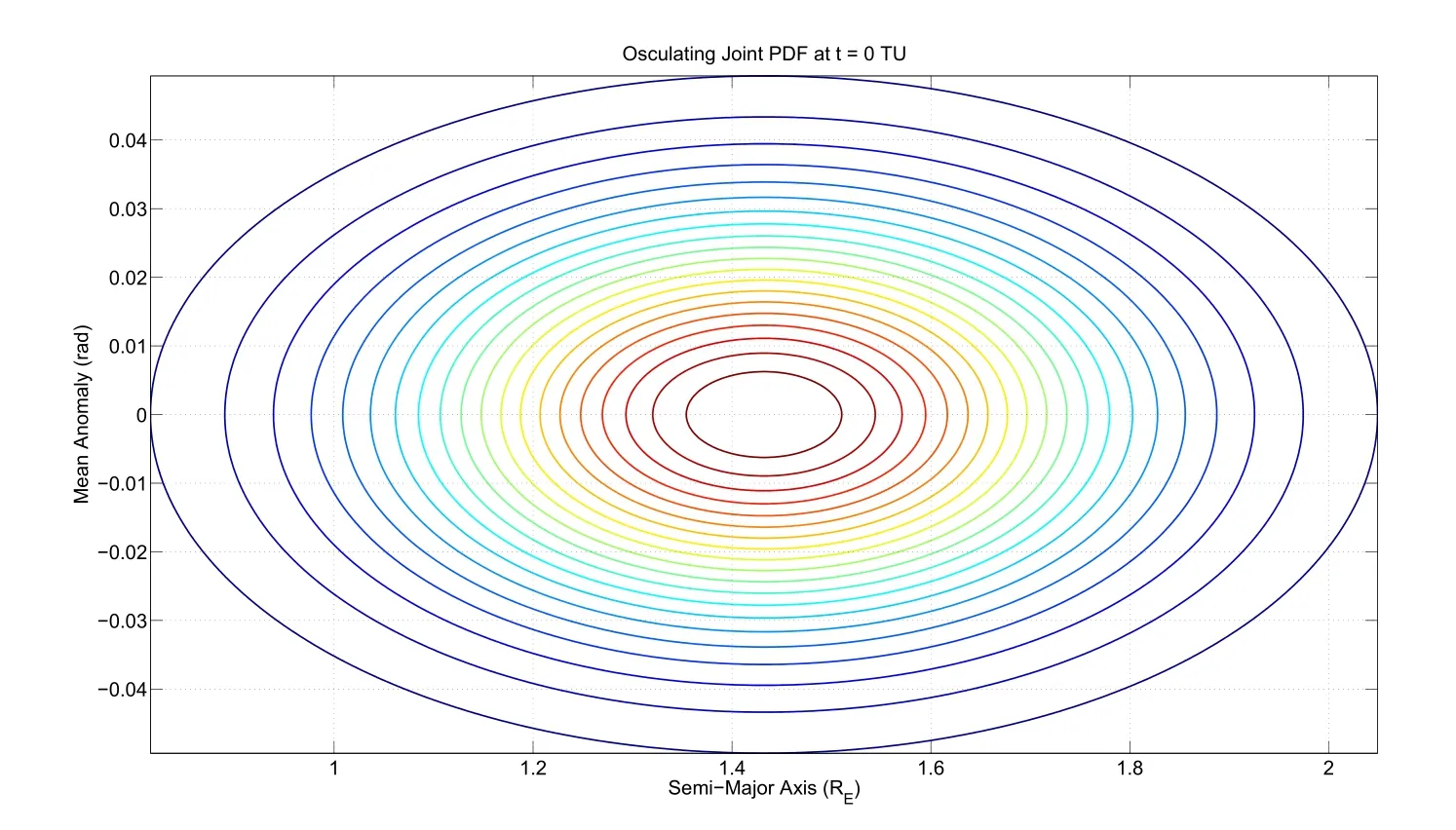
Figure 1:Initial Uncertainty in the Semi-Major Axis and Mean Anomaly

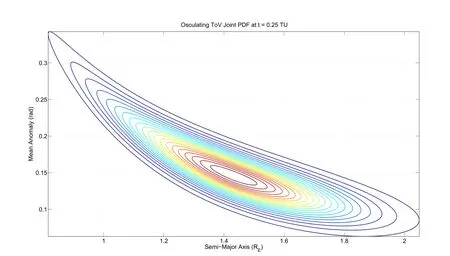
Figure 2:Joint(Conditional)Density between Semi-Major Axis and Mean Anomaly for Circular Orbit at t=0.25 TU

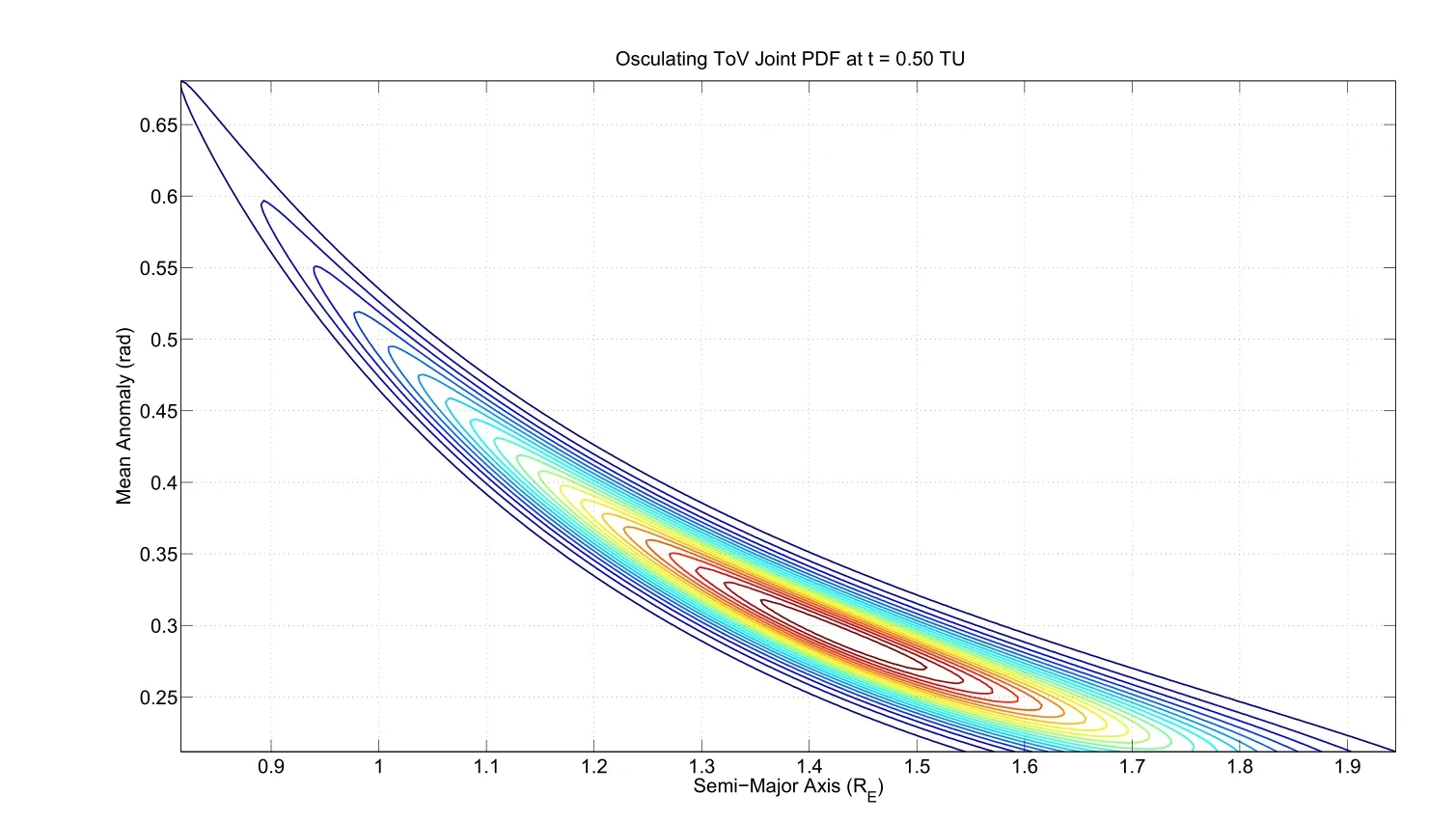
Figure 3:Joint Density between Semi-Major Axis and Mean Anomaly for Circular Orbit at t=0.5 TU

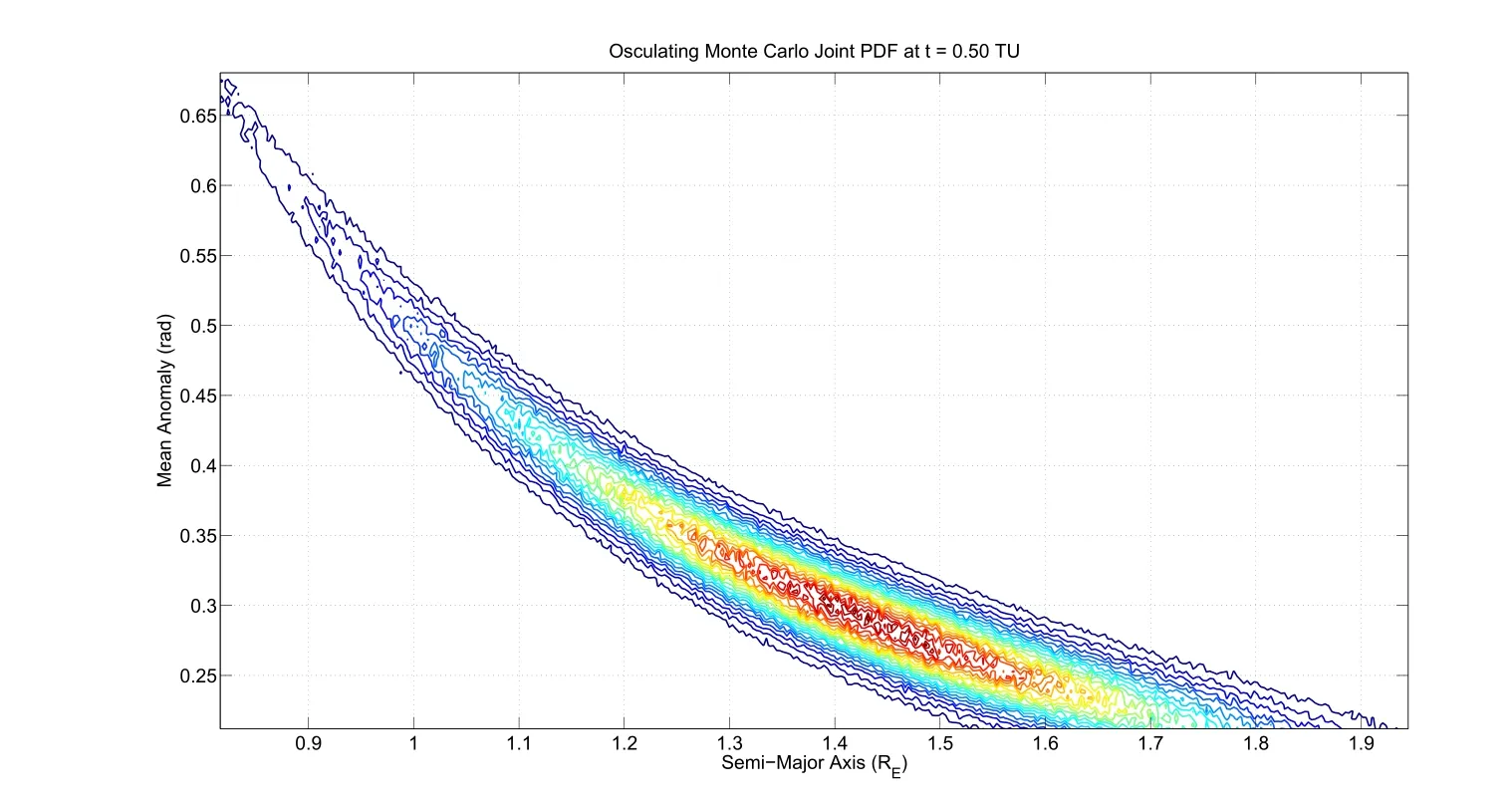
Figure 4:Approximate PDF Computed from Monte Carlo Simulations for Circular Orbit at t=0.5 TU

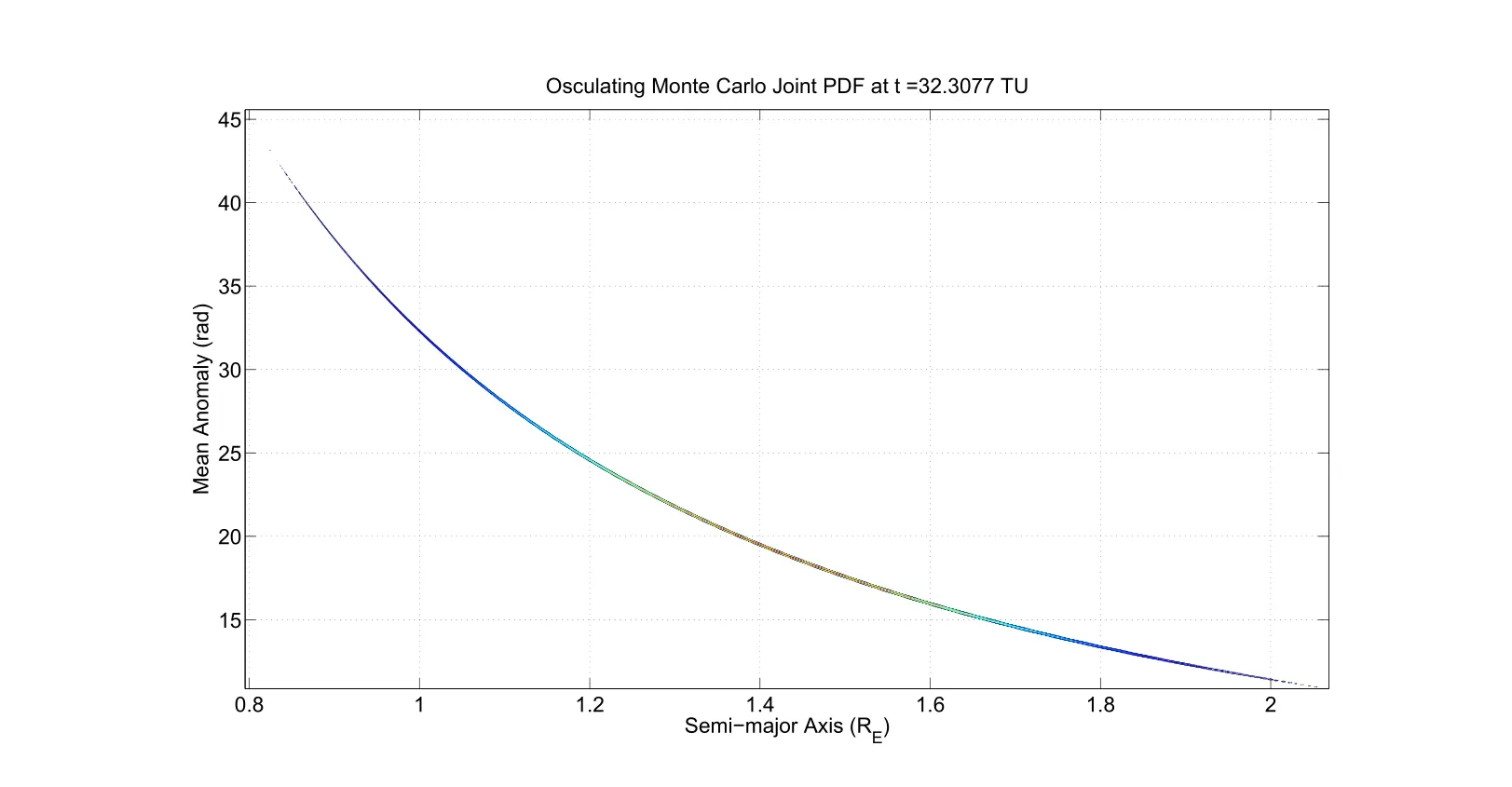
Figure 5:Approximate PDF Computed from Monte Carlo Simulations for Circular Orbit at t=3 Period(32 TU)

Figure 6:Approximate PDF Computed from Analytic Solution for Circular Orbit at t=3 Period(32 TU)

Although the analytical solution derived in this paper is useful for uncertainty propagation for Keplerian motion,most physical space systems operate in non-Keplerian orbits.Earth oblateness(J2),atmospheric drag,third body gravitational perturbations and higher order zonal harmonics act as perturbation forces to influence the orbital motion of the spacecraft.To use the analytical solution process developed in this paper,we make use of analytical orbit theories that describe the long period and secular variations of the perturbed two body problem.Specifically,we make use of Brouwer’s solution(Brouwer-Lyddane theory)to the artificial satellite problem without drag in conjunction with the Liouville’s equation solution to provide an exact expression for the evolution of the mean orbital elements then transformed back to osculating space.Mean orbital elements express the secular variation of the zonal perturbed two-body dynamics.The osculating elements can be recovered from the propagated mean elements by adding back in the short and long period contribution to the motion.To this end,we discuss the fundamentals of Brouwer theory and define Lie transforms to derive the averaged equations in the next section.

6 Brouwer Theory and Mean Element Equations

One of the key perturbation forces experienced by artificial satellites is the effect of Earth’s oblateness on the orbital dynamics.Cowell’s method[Battin(1990)]is frequently employed and a special perturbation solution is obtained for the s-pacecraft using numerical integration.For uncertainty propagation applications,the special perturbation solution yields one particular trajectory and is frequently repeated millions of times(for a 6 dimensional problem)to yield high confidence histograms representing the approximate evolution of the probability density function.However,this approach is computationally expensive,especially when the system dimensionality becomes large.For conservative perturbations such as J2,analytical orbit theory can be used to provide a closed form approximate solutions to the artificial satellite problem with no drag.Brouwer(1959)enables a closed form solution for artificial satellite’s main problem(motion of a satellite about an oblate planet without drag).It uses canonical transformations to provide a solution for the secular and long period oscillation solutions to the main problem. During the late 50s,various analytical orbit theories were developed to study satellite motion under the influence of orbit perturbations.Garfinkel(1959)presents a closed form solution to the main problem using a modified potential for the oblate spheroid,while Kozai(1959)is quite similar to Brouwer theory but utilizes direct averaging.Vinti(1959)develops a closed form solution for the motion of a satellite about an oblate spheroid using Jacobian elliptic functions.Although Vinti theory is the most accurate closed form solution,its formal expressions involve Jacobian elliptic functions that makes working with them tedious.

We develop Brouwer theory to first order using an averaging approach that is based on the application of Lie transforms[Deprit(1969);Nayfeh(1973)]due to Deprit and Rom(1970)re-derived by Alfriend,Vadali,Gurfil,How,and Breger(2010)and Alfriend and Majji(2009)to construct the canonical transformations to the mean elements.This development establishes an analytical relationship between the osculating elements and the mean orbital elements.This analytical functional relationship allows for an initial osculating PDF to be transformed to mean element space,propagated using the transformation of variables’solution to Liouville’s equation,then transformed back to osculating space at the propagated point in time.

6.1 Averaging and Lie Series

Lie transforms form a systematic approach to develop canonical transformation between the variables(x,X)to(y,Y)where the Hamiltonian in the transformed variables possesses certain desired properties(i.e.,comprises of long period terms by averaging out the short period oscillations).By choosing an appropriate Hamiltonian in the“new”variables(hereby referred to as the Mean elements in this paper,with the required Hamiltonian being written as K(y,Y)),a Hamilton-Jacobi equation is solved to obtain the generating function that enables the requisite transformation. In astrodynamics problems involving analytical orbit theories,this transformation is constructed between osculating and mean orbital elements.Mean orbital elements are the first-order averaged equations that capture the secular variation of the constants of motion due to orbit perturbations.Lie transforms are defined as formal power series in terms of the small parameter ε given by

The Hamiltonian in the “old”variables(hereby referred to as the osculating elements,i.e.,(x,X))is given by

such that the canonical equations in terms of the osculating elements are given by Eqs.4 and 5.In the mean elements,the Hamiltonian is also expressed as a power series in terms of the small parameter given by

The generating function(to be determined)is also written in terms of the formal power series given by

that generates the implicit equations relating the mean and osculating elements by

Using the definitions of Lie transforms[Deprit and Rom(1970);Deprit(1969)],the first order term in the power series expansion of the phase variables in Eq.27 can be written as

By choosing the first order term in the transformed Hamiltonian K1to be the averaged energy function,short period terms are eliminated from the osculating elements and the mean elements(y;Y)are produced.High order approximations of the osculating elements can be obtained in a similar fashion,by retaining more terms in the power series expansion of the Lie transform[Deprit(1969);Deprit and Rom(1970)].As opposed to the Von-Zeipel method used by Brouwer(1959)and Nayfeh(1973),the Lie series recursions are highly amenable for implementations on a computer.We develop analytical expressions for the main problem by using Lie transform in conjunction with Lyddane’s modification of Brouwer theory.The resulting developments are discussed below.

6.2 First Order Transformation Relating Osculating and Mean Keplerian Orbital Elements

The theory of Lyddane(1963),is a reformulation of the original mapping of zonal perturbed mean elements to osculating elements developed by Brouwer(1959).The formulation was introduced by Lyddane to provide a more numerically stable transformation from mean element to osculating element space as inclination and eccentricity go to zero.To first-order of the dominant zonal perturbation,J2,one can transform between mean and osculating elements by simply flipping the sign,otherwise a differential correction scheme must be used to convert osculating elements to mean elements.

The first-order transformation between mean and osculating Keplerian orbital elements for the J2perturbed two body problem using Poincaré elements is reported since it is not explicitly stated in Lyddane’s presentation and it is derived also from Lie series[Alfriend and Majji(2009)].Long,Cappellari Jr.,Velez,and Fuchs(1989)present second order expansions of the mean orbital elements in terms of the osculating elements,however,the presentation is more appropriate for computer coding instead of analysis.This presentation is similar to that of Schaub and Junkins(2010)but with different equations for deriving the composite longitude and right ascension of the ascending node with the reasoning given where the equations are derived.For small eccentricity one could also use the approach of Tapley,Schutz,and Born(2004),where eccentricity,argument of perigee,and mean anomaly are replaced with e sin(ω),ecos(ω),and ω+M,andthelong-period terms are neglected.

It is customary to express the transformations relating mean and osculating orbital elements using Kepler elements,although the averaging has been carried out using other coordinate systems.Brouwer-Lyddane theory is useful to provide quick solution to compute satellite ephemeris,the solution provides a mechanism to derive mean orbital elements without including high order effects in the dynamical system[Walter(1967);Der and Danchick(1999)].The format of the algorithm follows that given by Schaub and Junkins(2010),where the transformed-to element space is denoted with a single prime and the initial space elements are unprimed.

When transforming between osculating and mean element spaces the modification made to Brouwer’s γ2variable is given by Eq.36.Other simplifying variables are given by Eq.37.The true anomaly variable for the initial domain is computed from the eccentric anomaly solution to Kepler’s equation if it is not already known.

The new domain’s semi-major axis is then computed from the first-order J2mapping given by Brouwer with the modified γ2variable as shown by Eq.38.The semi-major axis only contains secular and short-period results,this is important in understanding the form of the PDF as it evolves in time.

The long-period and short-period corrections for eccentricity are modified using Lyddane’s expressions to avoid errors when the eccentricity is small.The modifications are given by Eq.39.The short-period results for eccentricity are given by Eq.40 and since the long-period eccentricity and inclination are related by a scale factor,both are given in Eq.41.The short-period results for inclination are given in Eq.42.If in the present domain,true anomaly is not available it is computed from mean anomaly and eccentricity either by Newton’s method for Kepler’s equation[Schaub and Junkins(2010)],or the Fourier-Bessel function expansions in terms of the eccentricity[Battin(1990)].

The long and short-period terms of mean anomaly are given by Eqs.43 and 44.

The new domain eccentricity and mean anomaly can be computed using Eq.45.

The long and short-period terms of right ascension of ascending node are given by Eqs.46 and 47.

The long and short-period terms of argument of perigee are given by Eqs.48 through 51.The first part of short-period term of argument of perigee and the short-period terms of mean anomaly differ by a factor of η.

The composite longitude is computed by Eq.52.When the short-period terms of mean anomaly and the first short-period term of argument of perigee are added together the result of?η−2−η−1?/e has eccentricity as a factor not divisor when simplified so the expression goes to 0/1 since?1−e2?→1 faster than e→0 as e → 0,see Brouwer’s remark after his Equation(23)[Brouwer(1959)],Eq.53 shows the rearrangement effect.It is here that the derivation differs from that of Schaub and Junkins(2010)because the reference assumed this sum to be zero.

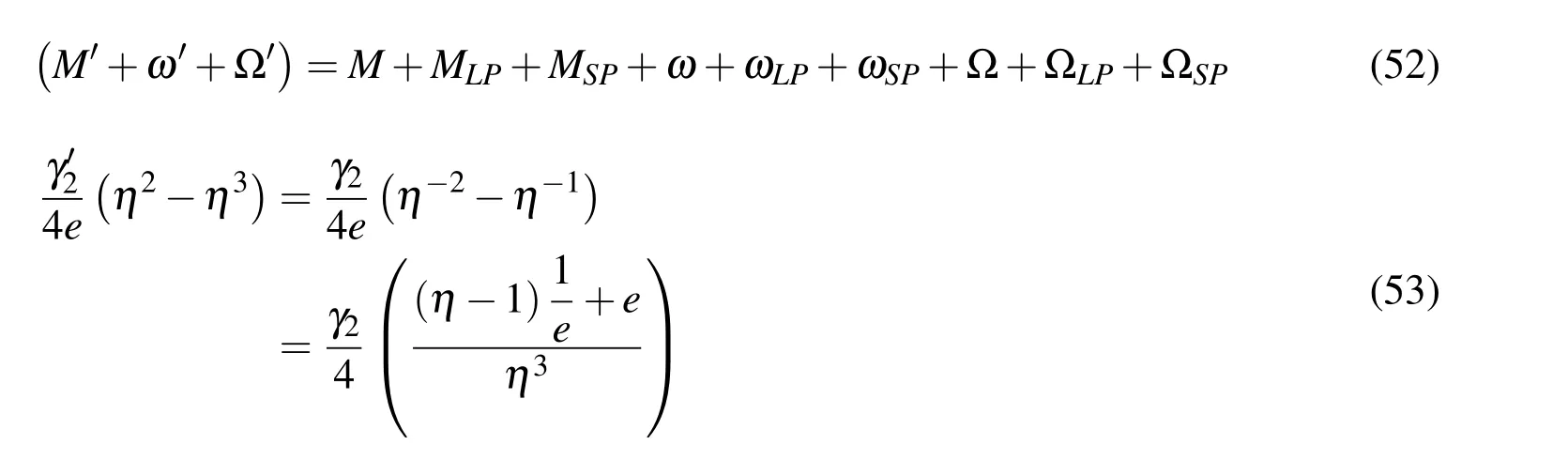
The new domain inclination,right ascension of ascending node,and argument of perigee are computed from Eqs.54 and 55.When computing the transformed argument of perigee,Eqs.52 and 53 are applied to compute the parenthetical term then the transformed Mean Anomaly solution from Eq.45 and transformed Right Ascension of Ascending Node solution from Eq.55 are subtracted out.

An alternative but similar implementation of Lyddane’s modification to Brouwer’s theory is given by Long,Cappellari Jr.,Velez,and Fuchs(1989).Both versions were implemented and tested with differences found to be on the order of 1×10−9for each element’s respective units.The results of the Lyddane conversion between first order elements was also compared to those of Aksnes(1972)who presented numerical results as well as explicit expressions of Izsak’s approach which utilized Hill variables[Izsak(1963)]to reduce the complexity of the Brouwer and Lyddane solutions.

For an example of conversion between orbital element space,the Two-Line element(TLE)of Hubble Space telescope(HST)was converted from mean to osculating then back to mean space with the results shown in Tab.2.For simplicity,the mean motion from the TLE was assumed to be the Brouwer value and not the Kozai value.The results would be similar if one converted from Kozai mean motion to Brouwer mean motion then computed the orbital element results.The element conversion errors of mean to osculating back to mean(M→O→M)and osculating to mean back to osculating(O→M→O)are shown in Tab.3.The value of J2is approximately 0.00108,when converted to degrees from radians the value is approximately 0.0620.The tables show that the errors of semi-major axis,eccentricity,right ascension of ascending node,and inclination angle are below the order of J2.The errors of the anomalies and argument of perigee are on the order of J2,approximately 0.09 to 0.12 degrees.

Table 2:Keplerian Elements for HST TLE for Day 23 of Year 2011

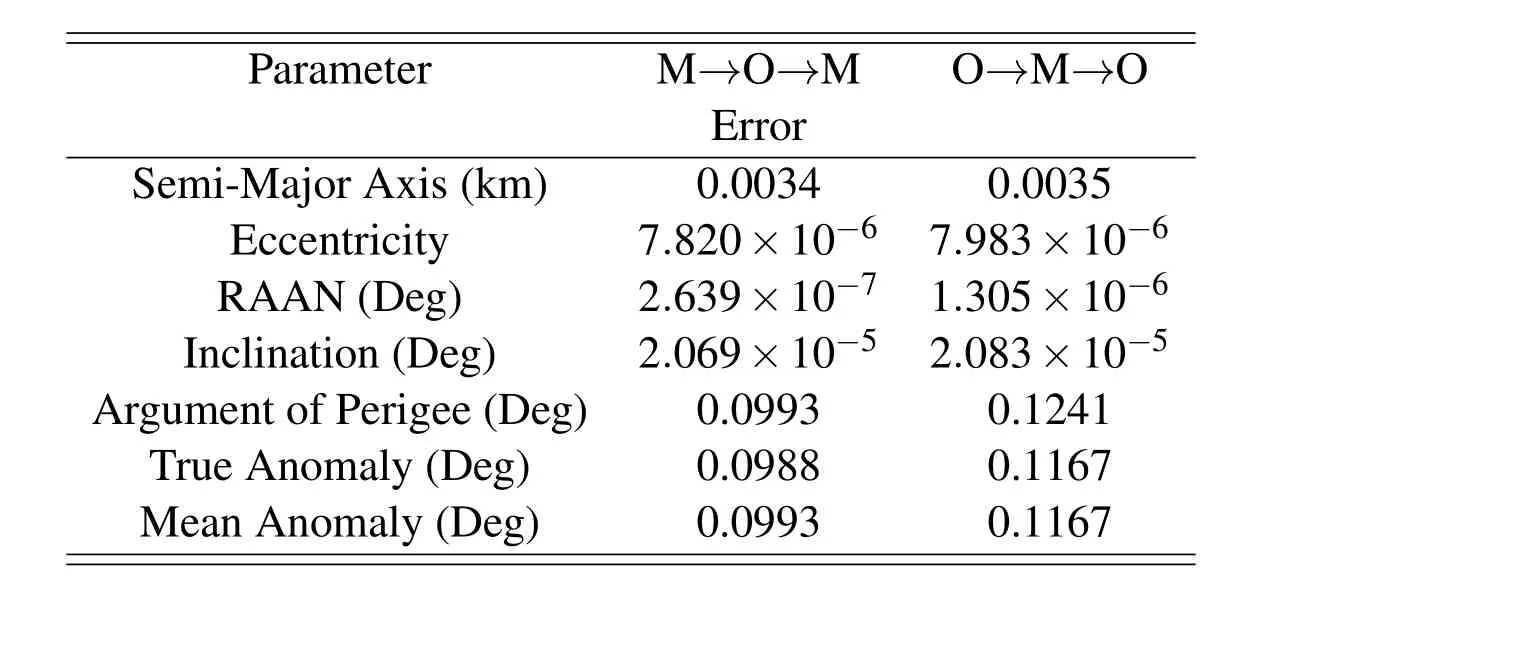
Table 3:Conversion Errors of HST TLE for Day 23 of Year 2011

7 Evolution of PDFs in the Main Problem

The analytical solution of Liouville’s equation to the averaged mean elements derived for the main problem of artificial satellite theory is now examined.The averaging process establishes a smooth and differentiable mapping between the osculating orbital elements and the mean orbital elements.Further,dynamical singularities in the mapping process are eliminated using the Poincaré elements following the developments of Lyddane.Two orbits are considered to demonstrate the nonsingular nature of the mean equations and to outline the uncertainty propagation in the main problem of artificial satellite theory.The first case uses an osculating eccentricity of 0.001 making the orbit nearly circular.The second case considers the uncertainty propagation problem for a more eccentric orbit,e=0.2.Initial conditions for both cases and the statistics associated are shown in Tab.4 with the osculating Kepler element values listed.Again,the large standard deviation used in the initial uncertainty associated with the semi-major axis is used for demonstration purposes.Consequently,it is possible that a part of the PDF volume consists of solutions that go through the Earth.For more realistic Cartesian,Keplerian,and mean state uncertainties please see Weisman,Majji,and Alfriend(2014b)where the state uncertainties were derived from typical sensor measurement uncertainties and the Herrick-Gibbs initial orbit determination process utilizing the transformation of variables technique and Weisman and Jah(2014)for angles-only initial orbit determination uncertainty transformation and sensitivity to measurement spacing.Similar to the two body problem,approximate PDFs are generated by using Monte Carlo simulations.Again,1×106sample points of the osculating orbital elements are computed using a special perturbation solution to the Lagrange planetary equa-tions.The osculating orbital element samples are then used to compute the corresponding mean orbital elements using Brouwer-Lyddane theory[Lyddane(1963)]at each representative sample time of interest.Plotting contours of the histograms in the mean orbital element space upon normalization provides sampled data on the approximate PDF derived from the simulations.This is compared with the analytically derived PDF from the solution to Liouville’s equation associated with the mean orbital elements.

Tab.4 gives the initial conditions for the osculating orbit elements which are transformed to mean element space via the first-order transformation given by Lyddane(1963).The reduction in dimensionality obtained in case of the two body problem does not exist for the J2perturbed dynamics because the mean and osculating orbital elements are functions of all the orbital elements in general.Further,the determinant of the Jacobian of the transformation between osculating and mean is not constant over volume as is typically assumed when one applies the similarity transformation,i.e.inertia tensor rotation[Schaub and Junkins(2010)].This is because of the averaged Hamiltonian used by the mean orbital elements,detailed discussion on the nonconstant nature of the determinant of the Jacobian is presented in our previous work[Weisman,Majji,and Alfriend(2014a)].

Table 4:Initial Conditions of Osculating Keplerian Elements

The approximate PDF of the mean orbital elements at 0.5TU obtained from Monte-Carlo simulations for the near circular orbit in the presence of J2perturbation is plotted in Fig.8.This is compared with the exact analytical PDF computed from the solution to Liouville’s equation using Brouwer-Lyddane theory,Fig.7.Agreement to plotting accuracy can be noted by figure inspection.Comparisons of other conditional density functions can be carried out in the same fashion.We do not present those results to conserve space.The conditional PDF for the perturbed problem is qualitatively similar to the unperturbed two-body problem but,is not identical(to within plotting accuracy).The J2perturbation shifts the dominant mode(shown in red)to the left indicating a shift in the averaged mean anomaly space of the entire ensemble of trajectories represented by the uncertainty volume,at t=0.5TU the red area is closer to the semi-major axis value of 1.2,Fig.3.A straightforward application of Brouwer’s theory will not work for some of the orbits considered in this uncertainty analysis,due to the near zero eccentricity singularity of the Delaunay elements used by the Brouwer.We demonstrate that the use of Brouwer-Lyddane theory enables us to escape from these singularities since our calculations are carried out in the Poincaré element space.

Figure 9:Mean Results of Monte Carlo Analysis for Eccentric Orbit

Figure 10:Mean Results of Transformation of Variables Analysis for Eccentric Orbit

Figure 11:Mean Results of Monte Carlo Analysis for Eccentric Orbit

Figure 12:Mean Results of Transformation of Variables Analysis for Eccentric Orbit

To examine the effects of nonlinearity,we now compare the exact analytical PDF computed from the analytical orbit theory applied to an orbit with mean eccentricity of e=0.2.Using a propagation time of t=0.5TU,an approximate(conditional)PDF of the mean orbital elements generated by using Monte Carlo simulations is shown in Fig.9.This is compared with the analytical solution obtained using the methods developed in this paper plotted in Fig.10.

Figure 13:Osculating Results of Transformation of Variables Analysis for Eccen tric Orbit after 3 Orbital Periods

As opposed to some methods for uncertainty propagation,the proposed solution is valid for all propagation times(over any number of orbital time periods).Uncertainty propagation solutions based on the state transition tensors[Fujimoto,Scheeres,and Alfriend(2012);Park and Scheeres(2006);Majji,Junkins,and Turner(2008a)]require high order for accurate,long term propagation.Other methods require accurate domain determination[Kumar,Chakravorty,and Junkins(2010)]and adaptive weight function management[Terejanu,Singla,Singh,and Scott(2008)].Figs.11 and 12 present the approximate density functions using Monte Carlo simulations and the analytical solution for the mean elements at time t=3TU.Comparison of the approximate PDFs shows significant agreement between the transformation of variables solution and the Monte Carlo analysis,as it should since the Monte Carlo is,in essence,sampling from the transformation of variables probability density function solution.Fig.13 shows the propagation analysis using the transformation of coordinates solution to Liouville’s equation after 3 orbital periods.

8 Conclusion

In this paper,the transformation of variables technique was shown as an effective means for transforming and propagating state uncertainty for the motion of a space object subject to two-body acceleration only as well as Earth’s J2perturbation.The transformation of variables technique for the probability density function description and propagation was used in conjunction with canonical transformations and Hamiltonian mechanics to exploit dynamics of the system and reduce the dimensionality of the problem during the propagation phase.After propagation,the technique is then utilized to map the propagation probability density function to the state domain of choice without loss of information even when the mapping is nonlinear.The transformation of variables technique was shown to generate the solution to Liouville’s equation which is the diffusion free reduction of the Fokker-Planck equation for the time evolution of a state vector’s probability density function.The analytic solution of the propagated probability density function yielded by the transformation of variables technique was shown to agree with the Monte Carlo sampling solution using numerical integration.

The transformation of variables technique was demonstrated as an effective method for taking advantage of a system’s behavior for state uncertainty propagation,i.e.instead of numerically integrating the Liouville equation for two-body dynamics in Cartesian space one can simply transform uncertainty into Keplerian element space and use mean anomaly to propagate the uncertainty.Likewise,for the J2perturbed problem,one can utilize Brouwer-Lyddane mean element theory to propagate the probability density function for mean mean anomaly,mean argument of perigee,and mean right ascension of the ascending node then transform the probability density function back into osculating space instead using numerical integration.

Aksnes,K.(1972): On the use of the hill variables in artificial satellite theory:Brouwer’s theory.Astronomy and Astrophysics,vol.17,pp.70–75.

Alfriend,K.T.;Majji,M.(2009):Lie series and averaging with applications to brouwer theory.Lecture Notes for Advanced Astrodynamics,2009.

Alfriend,K.T.;Vadali,S.R.;Gurfil,P.;How,J.P.;Breger,L.S.(2010):Spacecraft Formation Flying:Dynamics,Control,and Navigation. Elsevier,Burlington,MA.pp.25,43-46,160-168,338-351.

Awad,A.;Narang-Siddarth,A.;Weisman,R.M.(2016): The method of multiple scales for orbit propagation with atmospheric drag.InAIAA Science and Technology Forum and Exposition(SciTech 2016),San Diego,CA.AIAA-2016-1370.

Battin,R.H.(1990):An Introduction to the Mathematics and Methods of Astrodynamics.Education Series.American Institute of Aeronautics and Astronautics,Washington,D.C.,.

Brouwer,D.(1959):Solution of the problem of artificial satellite theory without drag.Astronomical Journal,vol.64,no.1274,pp.378–396.

Deprit,A.(1969): Canonical transformations depending on a small parameter.Celestial Mechanics,vol.1,no.1,pp.12–30.

Deprit,A.;Rom,A.(1970): The main problem of artificial satellite theory for small and moderate eccentricities.Celestial Mechanics,vol.2,pp.166–206.

Der,G.J.;Danchick,R.(1999): Conversion of osculating orbital elements to mean orbital elements.Technical Report NASA-CP-3333,NASA Goddard Spaceflight Center,1999.

Evans,L.C.(1998):Partial Differential Equations.Graduate Studies in Mathematics.American Mathematical Society,Providence,RI.

Fujimoto,K.;Scheeres,D.;Alfriend,K.(2012):Analytical nonlinear propagation of uncertainty in the two-body problem.Journal of Guidance,Control,and Dynamics,vol.35,no.2,pp.497–509.

Garfinkel,B.(1959):The orbit of a satellite about an oblate planet.Astronomical Journal,vol.64,no.1274,pp.353–356.

Gibbs,J.W.(1902):Elementary Principles in Statistical Mechanics.Charles Scribner’s Sons,New York.

Goldstein,H.;Poole,C.;Safko,J.(2002):Classical Mechanics.Addison Wesley,San Francisco,CA.,3rd edition.pp.16-24,34-36,45-47,337-338,334-338,341-347,353-356,368-375,377-408,419-421.

Halder,A.;Bhattacharya,R.(2011): Dispersion analysis in hypersonic flight during planetary entry using stochastic liouville equation.Journal of Guidance,Control and Dynamics,vol.34,no.2,pp.459–474.

Izsak,I.G.(1963): A note on perturbation theory.Astronomical Journal,vol.68,no.8,pp.559–561.

Izzo,D.(2006):Statistical distribution of keplerian velocities.Journal of Guidance,Control,and Dynamics,vol.29,no.1,pp.298–305.

Junkins,J.L.(1997): Adventures in the interface of dynamics and control.Journal of Guidance,Control and Dynamics,vol.20,no.6,pp.1058–1071.

Junkins,J.L.;Akella,M.R.;Alfriend,K.T.(1996): Non-gaussian error propagation in orbital mechanics.Journal of Astronautical Sciences,vol.44,no.4,pp.541–563.

Junkins,J.L.;Singla,P.(2003):How nonlinear is it?Journal of Astronautical Science,vol.52,no.1-2,pp.7–60.

Junkins,J.L.;Singla,P.;Mortari,M.;Bottke,W.;Durda,D.(2005): A study of six near earth asteroids.In Atluri,S.N.(Ed):Proceedings of the International Conference on Computational and Experimental Engineering and Sciences.ICCEES.

Kessler,D.J.;Cour-Palais,B.G.(1978):Collision frequency of artificial satellites:The creation of a debris belt.Journal of Geophysical Research,vol.83,no.2637-2646.

Kozai,Y.(1959): The motion of a close earth satellite.Astronomical Journal,vol.64,no.1274,pp.367–377.

Kumar,M.;Chakravorty,S.;Junkins,J.L.(2010): A semi-analytic meshless approach to the transient fokker planck equation.Probabilistic Engineering Mechanics,vol.25,no.3.

Kumar,M.;Chakravorty,S.;Singla,P.;Junkins,J.L.(2009):The partition of unity finite element approach with hp refinement for the stationary fokker planck equation.Journal of Sound and Vibration,vol.327,no.1-2,pp.144–162.

Long,A.;Cappellari Jr.,J.;Velez,C.;Fuchs,A.(1989): Goddard trajectory determination system(gtds)mathematical theory(revision 1).Technical Report NASA-CR-183462,NASA Goddard Spaceflight Center,1989.pp.5.43-5.63,8.13-8.16.

Lyddane,R.(1963):Small eccentricities or inclinations in the brouwer theory of the artificial satellite.Astronomical Journal,vol.68,no.8,pp.555–558.

Majji,M.;Junkins,J.L.;Turner,J.D.(2008):High order keplerian state transition tensors.InAAS/AIAA F.Landis Markley Astronautics Symposium,Cambridge,MD.AAS 08-270.

Majji,M.;Junkins,J.L.;Turner,J.D.(2008): A high order method for estimation of dynamic systems.Journal of Astronautical Sciences,vol.56,no.3,pp.401–440.

Majji,M.;Junkins,J.L.;Turner,J.D.(2010): A perturbation method for estimation of dynamic systems.Nonlinear Dynamics,vol.60,no.3,pp.303–325.Majji,M.;Junkins,J.L.;Turner,J.D.(2011):Measurement model nonlinearity in estimation of dynamical systems.Journal of Astronautical Science,vol.52,no.3.

Majji,M.;Weisman,R.M.;Alfriend,K.T.(2012): Solution of the liouville equation for keplerian motion:Application to uncertainty calculations.InAAS/AIAA Spaceflight Mechanics Conference,Charleston,SC.AAS 12-262.

Nayfeh,A.H.(1973):Perturbation Methods.Wiley Interscience Series.John Wiley&Sons.

Park,R.;Scheeres,D.(2006):Nonlinear mapping of gaussian statistics:Theory and applications to spacecraft trajectory design.Journal of Guidance,Control and Dynamics,vol.29,no.2,pp.1367–1375.

Risken,H.(1996):The Fokker Planck Equation:Methods of Solution and Applications.Springer Series in Synergistics.Springer-Verlag,New York,NY,2nd edition.

Schaub,H.;Junkins,J.L.(2010):Analytical Mechanics of Space Systems.American Institute of Aeronautics and Astronautics,Washington,D.C.„ii edition.Tapley,B.D.;Schutz,B.E.;Born,G.H.(2004):Statistical Orbit Determination.Elsevier,Burlington,MA.pp.230-233,244-245,251-258,493-497.

Terejanu,G.;Singla,P.;Singh,T.;Scott,P.D.(2008): Uncertainty propagation for nonlinear dynamic systems using gaussian mixture models.Journal of Guidance,Navigation,and Control,vol.31,no.6,pp.1623–1633.

Terejanu,G.;Singla,P.;Singh,T.;Scott,P.D.(2011):Adaptive gaussian sum filter for nonlinear bayesian estimation.IEEE Transactions on Automatic Control,vol.56,no.9,pp.2151–2156.

Vinti,J.P.(1959):New method of solution for unretarded satellite orbits.Journal of Research of the National Bureau of Standards-B.Mathematics and Mathematical Physics,vol.62(63)B,no.2,pp.105–116.

Walter,H.(1967):Conversion of osculating elements into mean elements.Astronomical Journal,vol.72,no.8,pp.994–997.

Weisman,R.(2012):Nonlinear Transformations and Filtering Theory for Space Operations.Ph.d.dissertation,Texas A&MUniversity,CollegeStation,TX,2012.

Weisman,R.M.;Jah,M.K.(2014):Uncertainty quantification for angles-only initial orbit determination.InAAS/AIAA Spaceflight Mechanics Meeting,Santa Fe,NM.AAS 14-434.

Weisman,R.M.;Majji,M.;Alfriend,K.T.(2011):Analytic assessment of sensor uncertainty for application to space object tracking and correlation.In62nd International Astronautical Congress:Space Debris Symposium,Cape Town,South Africa.IAC-11-A6.6.7-10729.

Weisman,R.M.;Majji,M.;Alfriend,K.T.(2014a):Application of the transformation of variables technique for uncertainty mapping in nonlinear systems.Celestial Mechanics and Dynamical Astronomy,vol.118,no.2,pp.129–164.

Weisman,R.M.;Majji,M.;Alfriend,K.T.(2014b):Analytic characterization of measurement uncertainty and initial orbit determination on orbital element representations.Celestial Mechanics and Dynamical Astronomy,vol.118,no.2,pp.165–195.

1Presented in Part at the 2015 International Conference on Computational and Experimental Engineering and Sciences(ICCES)Modeling in Engineering and Sciences Mini-Symposium:Computational Methods in Celestial Mechanics as paper ICCES 1520-150422180.

2This work was prepared as part of official Government duties and it not subject to U.S.copyright protection in the United States.

3Research Aerospace Engineer,Air Force Research Laboratory,AFRL/RVSV 3550 Aberdeen Ave.SE,Kirtland AFB,87117

4Assistant Professor,Mechanical and Aerospace Engineering Department,University at Buffalo,318 Jarvis Hall,Buffalo,NY,14260.

5TEES Research Professor,Aerospace Engineering Department,Texas A&M University,College Station,TX,77843-3141.