Stable and Minimum Energy Configurations in the Spherical,Equal Mass Full 4-Body Problem

D.J.Scheeres

Stable and Minimum Energy Configurations in the Spherical,Equal Mass Full 4-Body Problem

D.J.Scheeres1

The minimum energy and stable configurations in the spherical,equal mass full 4-body problem are investigated.This problem is defined as the dynamics of finite density spheres which interact gravitationally and through surface contact forces.This is a variation of the gravitationaln-body problem in which the bodies are not allowed to come arbitrarily close to each other(due to their finite density),enabling the existence of resting configurations in addition to orbital motion.Previous work on this problem has outlined an efficient and simple way in which the stability of configurations in this problem can be defined.This methodology is applied to the 4-body problem,where we find multiple resting equilibrium configurations and outline the stability of a number of these.The study of these configurations is important for understanding the mechanics and morphological properties of small rubble pile asteroids.These results can also be generalized to other configurations of bodies that interact via field potentials and surface contact forces.

Celestial Mechanics,N-body problem.

1 Introduction

Celestial Mechanics systems have two fundamental conservation principles:conservation of momentum and conservation of(mechanical)energy.While conservation of momentum is always conserved for a closed system,mechanical energy is often not conserved and can be dissipated through non-conservative internal interactions.Thus,for any closed mechanical system it makes sense to seek out what their local and global minimum energy configurations are at a fixed level of angular momentum.We can use the existence of these local and global minima to define what we consider stable states for a system,which provides a strict and robust limit for any mechanical system and is distinguished from particle motion systems inastrodynamics which often are only oscillatory stable and in fact do not minimize the total energy.

If this question is applied to the traditional N-body gravitational problem,however,it can be shown that there are no configurations for N≥3 that lead to a minimum value of energy for a fixed level of angular momentum Scheeres(2012).What is meant here is that the angular momentum is fixed at a given value and all possible energy values are considered for different configurations.For the N=2 body problem there is a well-known relation between the minimum energy of the system for a given angular momentum,but this is lost for N≥3.This is due to the point-mass nature of the traditional N-body problem,as when there are more than 3 bodies it is always possible to drive the potential energy of the system to−∞while maintaining a constant angular momentum.This issue is considered in the paper by Scheeres(2012),where it is shown that replacing point mass bodies with finite density,rigid bodies enables the system N-body gravitational problem to have unique minimum energy configurations.This occurs as now bodies can rest on each other,meaning that their relative gravitational potential energies are bounded from below.That paper explores this phenomenon for celestial mechanics systems and finds all possible relative equilibria for the 3-body problem assuming the bodies have equal size and density and are spherical.Among other results,it is found that the so-called“full”3-body problem with equal masses has seven distinct relative equilibria,five additional beyond the familiar orbiting Lagrange and Euler configurations.Out of these,only 3 can be stable and only one of these three can be the minimum energy configuration for a given angular momentum.An interesting result is that the relative stability of these minimum energy configurations changes as the angular momentum of the system is modified.

This paper applies a similar methodology to the 4-body problem,restricted so that the bodies are spheres of equal size and density.The computational issues related to the 4-body problem are significant,as even for the point-mass case the total number of relative equilibria are not known and are at best bounded,e.g.Hampton and Moeckel(2006).Since this paper only focuses on finding local and global minimum energy configurations as a function of angular momentum,we do not consider purely orbital relative equilibria,as by a theorem from Moeckel(1990)these can never be minimum energy configurations.Instead,we focus on resting configurations,or configurations that are separated into a mixture of two groups of bodies that orbit each other(motivated by the hypothesis in Scheeres(2012)).

The method used for our analysis relies on a novel application of the Cauchy Inequality to find a modified version of the Sundman Inequality.From this approach we define what we refer to as the minimum energy function,which is essentially the same function as Smale’s amended potential Smale(1970a,b),although the derivation of our result is more direct.The minimum energy function is defined for a given level of angular momentum and only involves internal degrees of freedom in the system.Thus,whenever this function is stationary or positive definite with respect to all degrees of freedom,then the system is in a relative equilibrium.Further,if the function is positive definite about this relative equilibria then the given configuration is stable.It can be shown that at a given angular momentum there may be multiple stable relative equilibria,in this case there is always a minimum energy configuration which corresponds to the lowest energy level that the system can exist in.

This paper reviews the derivation of the minimum energy function and its application to find relative equilibria and evaluate their stability.We then apply this methodology to the spherical,equal mass,full 4-body problem.Resulting from this analysis we find a number of distinct types of relative equilibria involving the bodies segregated into one or two agglomerations.The stability of these configurations are explored and the minimum energy configurations at any given value of angular momentum are identified.Following this,additional implications are reviewed and future questions for inquiry are identified.

2 Background

Before we specifically investigate potentially stable relative equilibria in the full 4-body problem we lay out a number of basic results that will be of use.Many of these results and theorems are taken directly from Scheeres(2012),but are repeated as they are needed for context.

2.1 Mechanical Quantities

Consider a set of N rigid bodies that interact gravitationally and which all have finite densities by definition.Of primary interest is to define the total kinetic energy,gravitational potential energy and angular momentum of this system.Also of interest is to compute the total moment of inertia and the polar moment of inertia of this N-body system.Since finite density distributions are assumed for each body we must also incorporate rotational kinetic energy,rigid body moments of inertia,angular velocities and explicit mutual potentials that are a function of body attitude,see Scheeres(2002).

In the following the ith rigid body’s center of mass is located by the position riand has a velocity˙ri.In addition to its mass mi,the ith body has an inertia dyadic Ii,an angular velocity vector Ωiand an attitude dyadic that maps its body-fixed vectors into inertial space,Ai.The basic quantities are then defined as[Scheeres(2012)]:

This alternate moment of inertia is of use in developing sharper limits for the Sundman Inequality later.

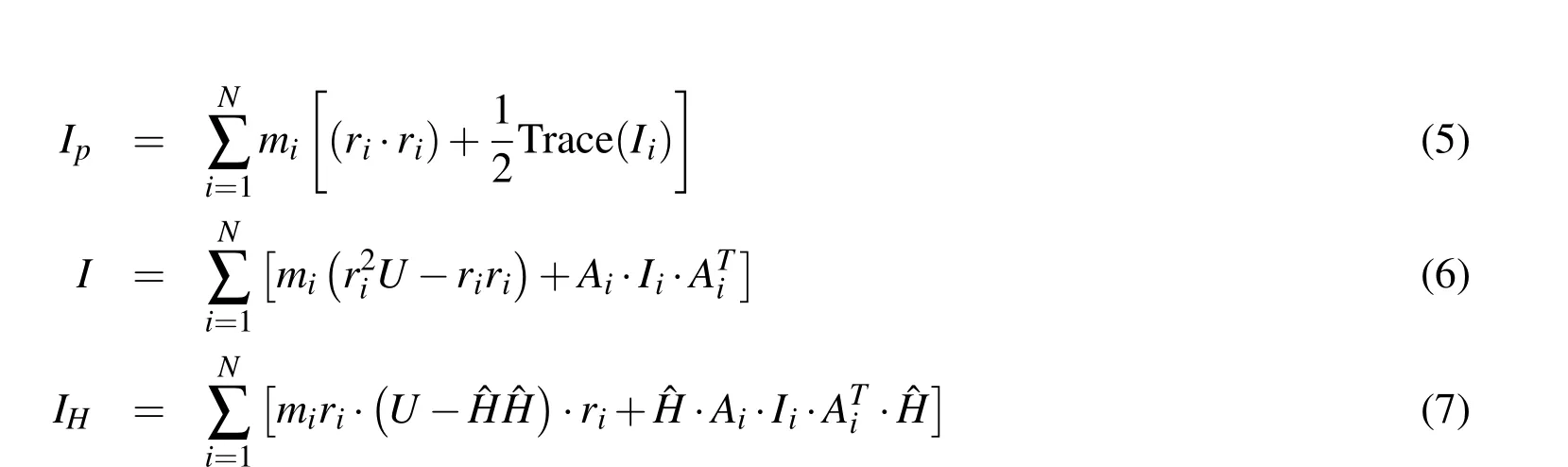
In the above the inertia dyadics are all specified in a body-fixed frame and thus are constant,the Uijare mutual potentials between two different rigid bodies i and j and are only a function of their relative position and relative attitude,Aij,equal to ATj·Ai,and which transfers a vector from the body i frame into the body j frame.For point mass density distributions all of the moments of inertia disappear and Ip=IHif the bodies and their velocities all lie in a common plane.Also,for spherical symmetry for all N masses,we can take A as the identity matrix.

The kinetic energy,moments of inertia and angular momentum can also be stated in relative form between the center of masses(assuming barycentric coordinates and applying Lagrange’s Identity),leaving the rotational components in their current form.

2.2 Finite Density Sphere Restriction

This paper focuses on the sphere-restriction of the Full-Body problem,where all of the bodies have finite,constant densities and spherical shapes defined by a diameter di.This allows for considerable simplification of the mutual potentials,although the rotational kinetic energy,moments of inertia and angular momentum of the systems are still tracked.In this case the moment of inertia of a constant density sphere is mid2i/10 about any axis and the minimum distance between two bodies will be dij=(di+dj)/2.The resultant quantities for these systems are

with the two different versions of the moment of inertia

2.3 Energy Dissipation Interaction Models

Implicit in these discussions,although not explicitly incorporated into the interaction models,are the dissipative effects of surface Coulomb and rolling friction and the tidal distortion of gravitationally attracting bodies.These physical effects serve a dual purpose,in that they will tend to synchronize collections of bodies,either resting on each other or orbiting each other,and will also dissipate excess energy in the system.This is needed in order for a resting collection of particles to dissipate relative motion between each other when in contact and thus also represents one possible mode of energy dissipation.Inclusion of this notional model ensures that contact configurations will,when reduced to their minimum energy state,all rotate at a common rate.

It is also possible to dissipate energy and synchronize spin rates even if bodies are not in contact.Tidal distortions arising from relative motion between gravitationally attracting bodies will also transfer angular momentum across the system and cause the dissipation of energy.Even if these effects are small,as they can be for asteroidal bodies,see Goldreich and Sari(2009),they are pervasive and will cause continual dissipation of energy for systems that are not in a relative equilibrium state.

The ubiquity and pervasiveness of energy dissipation in the solar system and its role in the long-term evolution of bodies of all sizes motivates the main question concerning the minimum energy states for celestial mechanics systems at a given value of angular momentum.We do not account explicitly for the physics for these assumed-to-be-present non-conservative effects,but nonetheless rely upon them to reduce the system energy to at least one of the local energy minima consistent with the prescribed angular momentum.

2.4 The Sundman Inequality and Minimum Energy Function

The fundamental result for this study is found by the definition of a modified version of the Sundman Inequality,which uses the moment of inertia IHinstead of the usual polar moment of inertia Ip.We repeat,without proof,two Theorems that are established in Scheeres(2012),as they motivate the following analysis.

Theorem 1.H2≤2IHT≤2IpT

The outermost inequality is the usual Sundman Inequality,but the sharper limits are new and are distinct for the full body problem.

The Sundman Inequality provides an important,and sharp,lower bound on the system energy for a given angular momentum.The derivation of this is simple,but the result has not been extensively used.

Given the defined minimum energy function a rigorous approach can be formulated to the original question of what the global minimum energy configurations of a celestial mechanics system are.These are found by determining configurations where either all variations of the minimum energy function are zero or if configuration constraints exist by showing that all allowable variations only increase the minimum energy function.

With these results we can now investigate the problem at hand.

3 Minimum Energy Configurations

3.1 Definition of the Normalized System

This discussion is restricted to bodies having equal sizes and densities.Thus,all particles have a common spherical diameter d and mass m.Given this restriction the moment of inertia and potential energy take on simpler forms.

where m is the common mass of each body and d the common diameter.Then rij≥d for all of the relative distances.Now introduce some convenient normalizations,scaling the moment of inertia by md2and scaling the potential energy by Gm2/d.Then the minimum energy function is

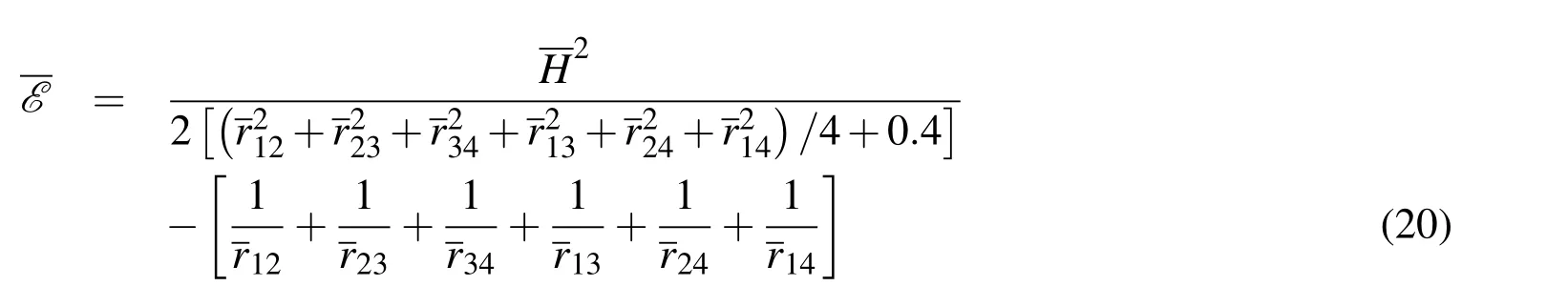
3.2 Hypothesized Relative Equilibrium Configurations

For the case of N=4 the number of possible configurations grows significantly as compared to the 9 unique configurations identified for the N=3 body problem[Scheeres(2012)].First of all,for orbital configurations the full set of relative equilibria for all mass values is not known and only bounded[Hampton and Moeckel(2006)].However,from Moeckel(1990)none of these will be energetically stable and thus can be left out of this analysis.Based on this same premise,and as articulated in the Hypothesis in Scheeres(2012),it can also be surmised that the only energetically stable orbital configurations will have the system collected in two orbiting clusters,further restricting the space to be considered a priori.Beyond this,one can also rely on principles of symmetry to identify the potential relative equilibrium candidates.An album of possible relative equilibrium configurations for the equal mass and size case is shown in Fig.1.These candidate configurations were identified by noting symmetries in the configurations but do not preclude the possibility of missed symmetric configurations or asymmetric configurations,which are sure to become more significant as the number of particles increases.

No assertion that all possible relative equilibria have been identified is being made,however the ones listed in Fig.1 are hypothesized to control the minimum energy configurations.To carry out a detailed analysis would require the development of appropriate configuration variables for the different classes of motion and the formal evaluation of stationary conditions and second variations.This is tractable in general,as the different possible planar configurations of the contact structures can all be described by two degrees of freedom.Some specific examples are given later.

Instead of taking a first principles approach,as was done for the N=3 case in Scheeres(2012),a number of alternate and simpler approaches to determining the global minimum configurations as a function of angular momentum are developed in this paper.In all of the following computations normalized values for the angular momentum,moment of inertia,gravitational potential and minimum energy function are assumed.The angular momentum is normalized by md2,the gravitational potential and the minimum energy function by Gm2/d,and the angular momentum H2by Gm3d.The common factor of 0.4 added to the moment of inertia IHarises from the moments of inertia from each of the spheres.

Figure 1:Candidate relative equilibria for the N=4 Full-body problem.Many other configurations are expected to exist,however these appear to control the minimum energy landscape.Note,we do not show any purely orbital relative equilibria as these are not expected to ever be stable.

3.3 Static Rest Configurations

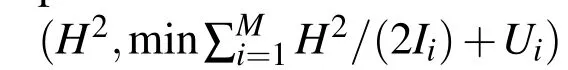
Alternately,one can directly determine the moments of inertia and the gravitational potentials of all of the different candidate configurations.Given two configurations,it is then simple to determine the angular momentum at which their minimum energies are equal,and thus where the transitions between these two configurations would occur independent of all other global results.Table 1 presents the computed polar moment of inertia and gravitational potential for each of the static configurations.

Finally,note that configuration“0”is a 3-dimensional configuration,and thus when its moment of inertia IHis computed a direction for evaluating the moment of inertia about its rotation axis must be defined,however the tetrahedron has a uniform moment of inertia which is equal about any arbitrary axis through its center of mass.All the other configurations lie in a plane with the rotation axis perpendicular to this plane(note that this always yields the maximum moment of inertia and thus minimizes the energy,all else being fixed).

Table 1:Table of polar moments of inertia and gravitational energies for each static configuration.

Assume two candidate configurations, i and j, then their minimum energy functions are equal for the same value of angular momentum if

The angular momentum at which this occurs can be solved for as

and represents the angular momentum at which the minimum of the two configurations switch.Inputing the values from Table 1 into this formula generates a transition table for the different static configurations.Table 2 shows the different transitions that occur between the static configurations.Figure 2 graphically shows the energy vs.angular momentum squared plot with the minimum energy configuration taking turns in number from 0 to 3.Figure 2 shows the normalized spin rate of these different minimum energy configurations,equal to H/I.Note that the higher energy configurations do not have faster spins,due to the redistribution of mass.Transitions also occur between these configurations and numbers 4 and 5,but these two are never minimum energy states.

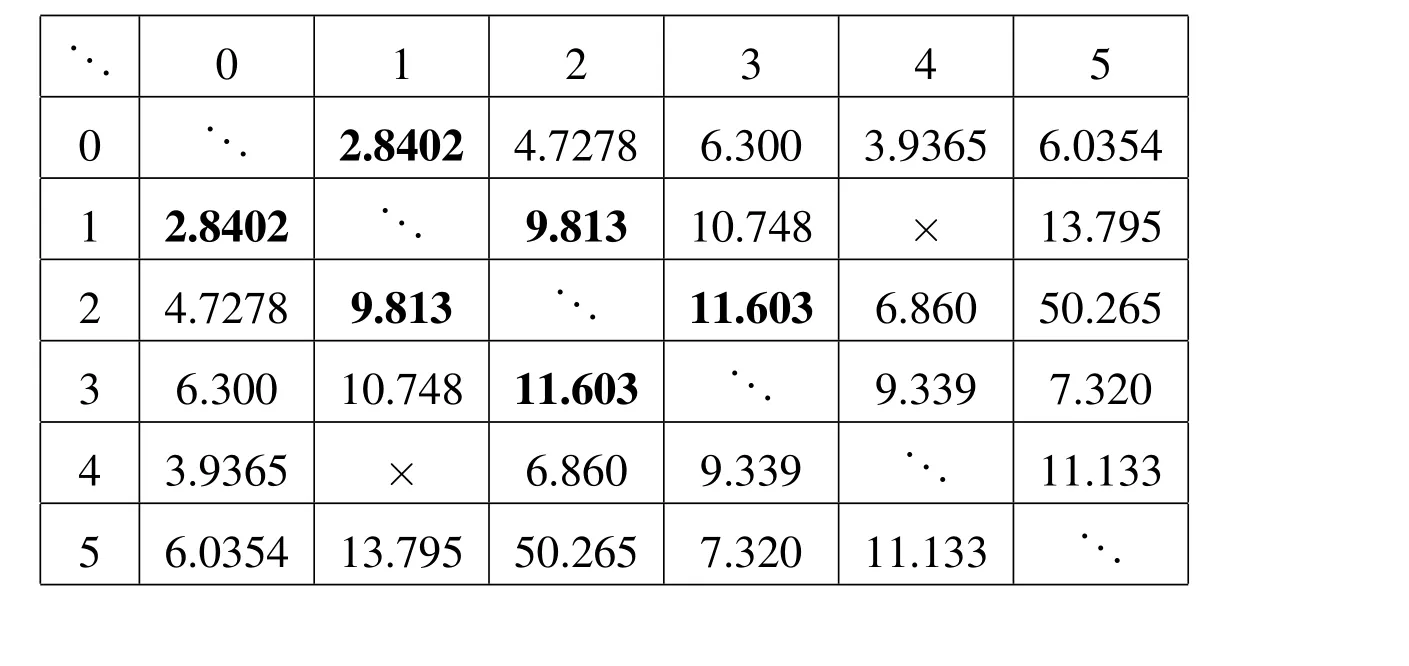
Table 2:Transition values of H2between different static resting configurations,with transitions leading to or from global minima indicated in bold.Note that as configurations 1 and 4 have the same moment of inertia,they never cross.

With this approach it is not possible to identify the precise transition points or the excess energy when the different states switch,unlike the more detailed analysis that can be given for the N=3 case[Scheeres(2012)].Evaluation of these transitions requires that the variable resting configurations be identified,as they mediate the loss and gain of stability for the various resting configurations.

3.4 Mixed Equilibrium Configurations

To identify the global minimum energy configurations it is also necessary to consider the mixed equilibrium configurations.Each different candidate configuration can be analyzed using a single degree of freedom.As an example,Fig.3 shows configuration D with its single degree of freedom identified.

For any of the mixed configurations the polar moment of inertia and the gravitational potential as a function of the distance between the components can be defined as d and represented as I(d)and U(d).Then the minimum energy function is E(d)=H2/(2I(d))+U(d).By definition,relative equilibrium will exist when∂E/∂d=Ed=0.This is expressed as a function of i and U as

Figure 2:Energy-Angular Momentum graph showing the different transitions between minimum energy static resting states(left).Normalized spin rates of the different resting configurations(right).For a 2 g/cm3density,a unit rotation rate corresponds to a～6.6 hour rotation period.

Equating this to zero solves for the angular momentum for a relative equilibrium as a function of the distance between the components,d.The functions I(d)andU(d)and their partials are listed below for configurations A through D,which are the most relevant to the discussion.In addition to these values the value ofH2is also given when the components are touching,which defines the angular momentum when a given static rest configuration(defined whend=1)fissions into the given mixed equilibrium configuration,and the energy of the system when this occurs.

Configuration A:

Figure 3:Mixed equilibrium configuration candidate D,showing its single degree of freedom,the distance d.

Configuration B:

Configuration C:

Configuration D:

3.5 Transitions Between Resting and Mixed Configurations

To start to sketch out the more detailed picture of transitions as a function of angular momentum several specific transition states are investigated.Specifically the angular momentum values when static configurations 0,1,2 and 3 either become stable,lose stability,or both are found.

3.5.1 Fission Transitions

First,given the results on the mixed relative equilibria the angular momentum values at which the different static configurations no longer exist,i.e.,when they fission,can be identified.Static configuration 1 terminates when the inner orbital configuration C collides with it.Similarly static configuration 2 terminates when the inner orbital configuration D collides with it.For static configuration 3,there are two possible configurations it could fission into,A or B.It is interesting to note that configuration A consistently has a lower energy than configuration B,however the static configuration 3 fissions into configuration B at a lower value of angular momentum.Thus,in terms of a sequence of local minimum energy configurations linked geometrically,A is isolated from the static configuration 3.This is discussed in more detail later.In Table 3 the fission conditions and the angular momentum and energy values at which these occur are listed.

Figure 4:The angular momentum squared(left)and energy(right)for mixed relative equilibria as a function of separation distance.

Table 3:Static Configurations and the Orbital Configurations they fission into.

Figure 5:Energy versus angular momentum for the orbital relative equilibria A through D.The endpoints show where these families terminate by touching the static resting configurations.There are portions of these curves where there exist two of the orbital equilibria for a given angular momentum,although for large enough angular momentum there is only one member per family.

3.5.2Stability Transitions

Of additional interest are the stability transitions for the various static configurations,specifically,the range ofH2where they are stable.Of specific interest are the values of angular momentum at which static configuration 0 becomes unstable and at which 1,2,and 3 become stable.These are dealt with in turn in the following.Figure 7 shows the different degrees of freedom that are considered in the following analysis.

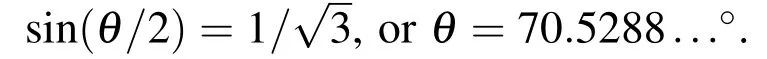
Figure 6:Spin rates for the different orbital relative equilibrium as a function of distance(left)and as a function of H2(right).

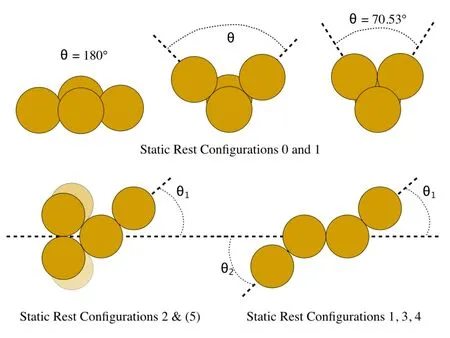
Figure 7:Degrees of freedom considered for stability analysis of the various static rest configurations.

The first variation of the minimum energy function with respect to this degree of freedom yields

At values of angular momentum larger than this the 0 configuration does not exist.Next settingθ=180◦yields the stationarity condition that corresponds to configuration 1.To evaluate the stability of this,take the second partial ofEand setθ=180◦to find

whereIH=2.4 now.Solving for whenδ2E≥0(note the minus sign in front)places the constraint on the angular momentum to be

at a corresponding energy ofE=−5.1155....Note that configuration 1 becomes stable before configuration 0 goes unstable1It is somewhat remarkable that these stability conditions are so easily obtained.Approaching this problem from a traditional mechanics approach,determination of the stability of either configuration requires the definition of moments acting on each particle,centripetal accelerations,and the like..

Stability of Static Configuration 2For this configuration suppose that the degree of freedom of interest is the angle defined in the plane from the nominal single contact particle to its location as it rolls on the contact particle.For a positive angle the distance from this particle to the two particles at the far end are

Then the moment of inertia and the gravitational potential are found as

EvaluatingδE,this equals zero forθ=0,as expected.Evaluating the second variation and evaluating when it is positive yields the condition for stability of configuration 2:

and has a corresponding energy ofE=−3.91904....

Stability of Static Configuration 3For configuration 3 the two general degrees of freedom allow the end particles to roll relative to the central pair.Define the outer-right body as 1,the outer left body as 2 and measure the anglesθ1andθ2as defined in Fig.7.The distances of the outer bodies to the furthest of the inner pair is

and the distance of these two bodies from each other is

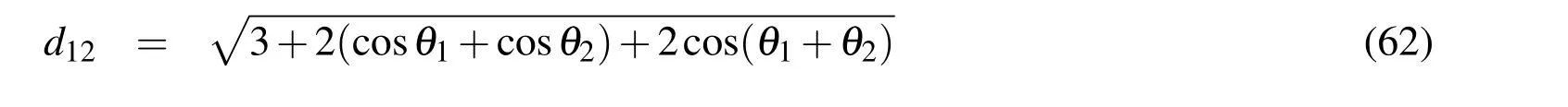
The moment of inertia and the potential energy are then

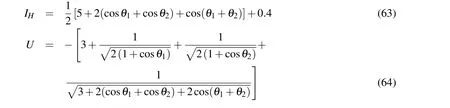
EvaluatingδE,this equals zero forθ1=θ2=0,again as expected.At this configuration the moment of inertia takes on a value of 5.4.

Evaluating the second variation and evaluating when it is positive yields the following entries that must be put into a matrix:

The two diagonal entries are equal as are the two off-diagonal entries.To be positive definite the following conditions must hold:

The controlling condition is the second one,and holds true forH2＞9.45 and has a corresponding energy ofE=−3.458333....

Stability of Static Configuration 5Finally,it is also of interest to study the stability of static configuration 5.This is similar to configuration 2,except the masses are equally spaced about the central body.This modifies the distances to

Repeating the analysis we now find the controlling condition for this configuration to be stable relative to variations in θ to be

However,if we analyze the variation δdE with respect to the distance of the rightmost particle from the rest of the configuration we find that the condition for stability in this direction is

Thus this configuration is never stable,as it would undergo fission prior to the angles becoming stabilized.It is important to note that this particular configuration is also never a minimum energy configuration,which is now to be expected given this result.

3.6 Transition Diagrams and Possible Outcomes

Given the above it becomes possible to map out the possible evolution of a collection of 4 particles as their angular momentum is increased or decreased.The following only focuses on the evolution as angular momentum increases,as there are a variety of different pathways and possible evolutions for the case of decreasing angular momentum,a topic for further research.Figure 8(left)shows a global view of all possible stable static relative equilibria and stable and unstable orbital equilibria,and shows a detail of this figure on the right indicating some of the transition points.

At an angular momentum of zero Configuration 0 is the only stable relative equilibrium.As angular momentum is increased Configuration 1 becomes stable at H2=2.217...and soon thereafter becomes the global minimum configuration.Configuration 0 remains stable until H2=3.92 when it ceases to exist.At this point there is an excess of energy in the system and it will evolve dynamically.If energy dissipation is present,however,it can only settle into Configuration 1,as this is the only stable relative equilibrium.Configuration 1 remains stable until ifssion into the unstable Orbital configuration C occurs at H2=13.737.During this evolution both configurations 2 and 3 become stable.Further,configuration 2,while the global minimum for an interval, fissions into Orbital configuration D at H2=13.684,before the fission of Configuration C occurs.Thus,a system smoothly following this evolutionary path will completely bypass Configuration 2.At this transition there are three possible stable relative equilibria that the system can settle into under energy dissipation.Configuration 3 and Orbital Configurations C and D.The system must shed the least energy to end up in Configuration 3,although this is not the global minimum.At this point,where the system settles becomes a dynamics question and cannot be addressed with the methods used in this study.The final settling place will likely depend on the manner in which energy is dissipated,the timescale over which the energy dissipation occurs,and as this dynamical system will be chaotic will also entail an element of randomization for specific simulations.It may be possible for the system to undergo mutual escape,separating into an N=1 and N=3 system.If the system settles into either Orbital Configuration C or D(which have nearly the same level of energy,with D having a slightly lower energy),then under continued increase of angular momentum the system will just evolve outwards maintaining the same orbital relative equilibrium.As the system grows arbitrarily large,the spin rate decreases to zero and the Lagrange-like rest configuration of the three bodies will remain stable.

If,instead,the system falls into the stable Static Configuration 3,then the evolution will continue as shown in Fig.8.Then,at H2=23.49 this configuration will fission into the inner,unstable Orbital Configuration B and again will have excess energy that will drive the dynamics of the system.Now there are four possible stable orbital configurations which the system can relax into,barring mutual escape.The energies of these relative equilibria are, in order,B,A,C,D.Again,which one it settles into will likely be a function of their energy dissipation interactions,timescale and chaotic evolution.If the system lands into either B,C or D then the resulting systems will remain stable for arbitrarily large values of angular momentum(i.e.,low spin rates for the separate components).If the system falls into configuration A then at some future spin rate the Euler rest configuration of the primary will likely become unstable and collapse into a Lagrange configuration,again having excess energy to dissipate.The likely final state of Orbit Configuration A under continued increase of angular momentum is then either Orbital Configurations C or D.

It is evident that stepping from N=3 to N=4 particles creates a much richer set of possible outcomes and removes the determinism that was present for the sphererestricted N≤3 Full Body problem.In addition to verifying the various hypotheses on relative equilibria and their stability transitions,it will also be necessary to investigate the actual dynamical outcomes of these simulations for different models of energy dissipation.The two most obvious dissipation methods will be impacts between the particles and tidal distortion of each other.Each in isolation will likely lead to different outcomes in some of these cases,although it would be of interest to discover whether any specific dynamical outcomes occur with high probability.

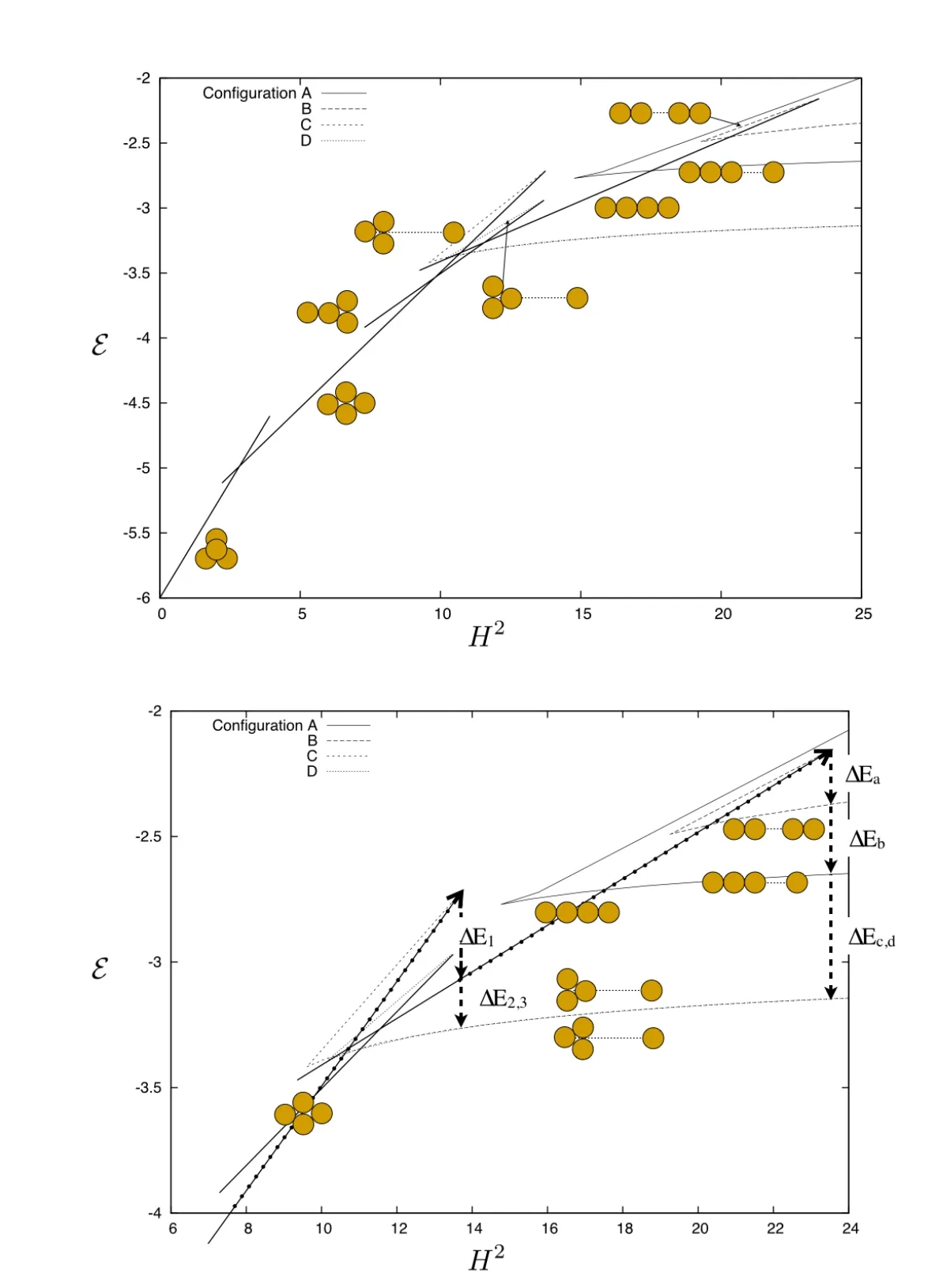
Figure 8:Energy versus angular momentum showing the relationship between the static resting configurations and the orbital configurations(left).The static configurations are only shown for when they exist and are stable.As angular momentum is increased or decreased there are transition points where multiple possible stable states exist.Detail of the energy-angular momentum curve shown on the right.

4 Conclusions

This paper computes and analyzes the minimum energy and stable configurations of the sphere,equal mass full 4-body problem in celestial mechanics as a function of angular momentum. It is shown that the complexity of the 4-body problem becomes significant,although specific results and outcomes can be found. The analysis poses more fundamental questions regarding how energy dissipation effects may shape the final states of systems that have been brought to stability transition points.

Acknowledgement:The author acknowledges support from NASA grants NNX11AP24G and NNX14AL16G from the Planetary Geology and Geophysics and the Near Earth Objects Observation programs,respectively.

Goldreich,P.;Sari,R.(2009): Tidal Evolution of Rubble Piles.Astrophysics Journal,vol.691,pp.54–60.

Hampton,M.;Moeckel,R.(2006):Finiteness of relative equilibria of the fourbody problem.Inventiones mathematicae,vol.163,no.2,pp.289–312.

Moeckel,R.(1990):On central configurations.Mathematische Zeitschrift,vol.205,no.1,pp.499–517.

Scheeres,D.(2002):Stability in the full two-body problem.Celestial Mechanics and Dynamical Astronomy,vol.83,no.1,pp.155–169.

Scheeres,D.(2012):Minimum energy configurations in the n-body problem and the celestial mechanics of granular systems.Celestial Mechanics and Dynamical Astronomy,vol.113,no.3,pp.291–320.

Smale,S.(1970): Topology and mechanics.i.Inventiones mathematicae,vol.10,no.4,pp.305–331.

Smale,S.(1970): Topology and mechanics.ii.Inventiones mathematicae,vol.11,no.1,pp.45–64.

1Department of Aerospace Engineering Sciences,The University of Colorado.

E-mail:scheeres@colorado.edu