Continued Fraction Cartesian to Geodetic Coordinate Transformation

J.D.Turner,A.Alnaqeband A.Bani Younes

Continued Fraction Cartesian to Geodetic Coordinate Transformation

J.D.Turner1,A.Alnaqeb1and A.Bani Younes1

A singularity-free perturbation solution is presented for inverting the Cartesian to Geodetic transformation.Conventional approaches for inverting the transformation use the natural ellipsoidal coordinates,this work explores the use of the satellite ground-track vector as the differential correction variable.The geodetic latitude is recovered by well-known elementary means.A high-accuracy highperformance 3D vector-valued continued fraction iteration is constructed.Rapid convergence is achieved because the starting guess for the ground-track vector provides a maximum error of 30 m for the satellite height above the Earth’s surface,throughout the LEO-GEO range of applications.As a result,a single iteration of the continued fraction iteration yields a maximum error for the satellite height of 10−11km.and maximum error for the geodetic anomaly of 10−9rad.The coordinate transformation is completed by non-iteratively recovering the satellite height and the geodetic anomaly.No Taylor expansions are introduced and no Jacobian sensitivity calculations are required.For all practical applications the new algorithm provides a closed-form solution.The accuracy and algorithmic performance of the proposed approach is compared with other state of the art algorithms.

Geodetic transformation,continued fraction,singularity-free.

1 Introduction

A frequent calculation for satellites in low Earth orbit(LEO)-to-geosynchronous Earth orbit(GEO)involve inverting transformations between 3D satellite Cartesian Earth centered coordinates and geodetic coordinates.Referring to Figure 1,the geodetic coordinates are given by(λg,φg,h),which denote the geodetic longitude of the satellite sub-point g,the geodetic latitude of the satellite,and the height of the satellite above the reference Earth elliptical surface along the surface normal from the geodetic ellipsoid to the satellite position.The transformation from geodeticcoordinates to Cartesian(xs,ys,zs)coordinates is given by,

Figure 1:Geodetic and Cartesian Coordinates.

2 Background

The nonlinear character of the Cartesian-to-Geodetic transformation problem makes it a continuing challenge for the community.The analytic complexity of the problem arises because the geodetic latitude and satellite height solution algorithms are coupled and highly nonlinear.The solution for the geodetic longitude,however,is elementary and non-iterative.Most algorithms use the geodetic coordinates as adjustable components.Numerical problems are often encountered near the Poles,for ϕ near 90 or-90 degrees.The most common numerical problem encountered arises from the need for handling sensitive quartic polynomial solutions.For example,Fukushima(1999),Borkowski(1989),Pollard(2003)and Lin and Wang(1995)have all encountered these challenges.To overcome these issues three classes of methods have been proposed:(i)closed-form solutions for cubic and quartic polynomials,(ii)perturbation methods,and(iii)successive approximation algorithms.The closed-form class of solution algorithms typically introduces sequences of trigonometric transformations that exploit identities to simplify the governing equation.The closed-form solution approaches share two common characteristics:(i)they are highly accurate,and(ii)they are frequently computationally expensive to evaluate.Important examples of this approach include:Bowring’s(1976)very well-known solution which introduces the reduced latitude as the iteration variable in Newton’s method;Petr and An-ek(1982)introduce a closed-form solution for a high-order algebraic equation;Pick and Simon(1985)develop an elliptic integralbased arc-length solution that that is computed based the geodetic height of the satellite;Fotiou(1998)presents an approximate closed-form solution which is obtained using a computer algebra system;and Vermeille(2004)presents a series solution by minimizing the distance between a point in space and its projection on the ellipsoid.

Given the nonlinear nature of the problem it is not surprising that many iterative techniques have been proposed.Early examples of this approach include the work of Heiskanen and Moritz(1998),which influenced the GPS-based need for the geodetic transformation methods developed by Kleusberg and Teunissen(1998),Hofmann-Wellenhof,Lichtenegger,and Collins(1997),and Strang and Borre(1997).Several innovative problem formulations have been proposed,including the work of Torque(1980),Borkowski(1989),Lin and Wang(1995),and Lupash(1985).Unfortunately,geometric singularities plague many of these iterative strategies.To avoid these troublesome singularities,several authors have investigated vector methods,including the work of Pollard(2002)and Feltens(2009).Zhang,Hsu,LI,Wang,Chai and Du(2005)present an elegant optimization-based strategy that finds the point on the surface of the ellipsoid being the projection of a point h distance away from the ellipsoid along the ellipsoidal surface normal,yielding straightforward solutions for the geodetic latitude and height.Third-order accelerated convergence techniques are considered by Fukushima(2006)known as Halley’s method.Recently,Turner(2009),Turner and Junkins(2011),Turner and Elgohary(2013),Turner,Elgohary,Majji,and Junkins(2011),and Elgohary and Turner(2012)have presented a very fast singularity-free second-order through fourth-order perturbation solution that introduces an artificial perturbation variable to transform the classical quartic solution problem into a singularity-free non-iterative quadratic equation problem.Ligas and Banasik(2011),presents the projection of a point on the reference ellipsoid for solving a system of nonlinear equations using second and third order Newton’s method.

The main contribution of this paper is the presentation of a non-iterative continued fraction expansion solution,where the iteration variable is the unconventional 3D satellite ground-track vector.A careful selection of an accurate starting guess for the algorithm is shown to yield convergence in one iteration for the entire LEOGEO range of applications.Additional iterations continue to improve accuracy far beyond existing measurement capabilities.No Taylor expansions are introduced and no Jacobian sensitivity calculations are required.As a result,the proposed method effectively provides a closed-form solution for the Cartesian-to-Geodetic transformation throughout the LEO-to-GEO range of applications.

3 Math Model for the Continued Fraction Expansion

Even with λgeasily obtained from Eq.1,it is obvious that the solutions for ϕgand h are nonlinearly coupled,and successive approximation strategies are required.The proposed continued fraction calculation begins from Figure 2 with the observation that the following closure exists

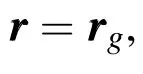
From Eq.2 it is also obvious that the satellite height is computed as

Introducing Eqs.4 and 5 into Eq.2,one obtains

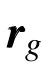
Or in the iteration form

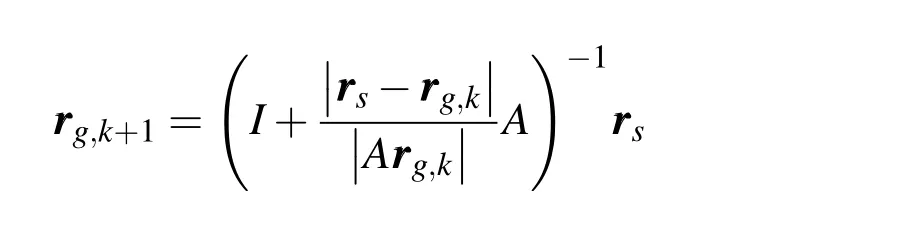
Figure 2:Geodetic vs.Geocentric Latitude.

3.1 Starting Guess for the continued Fraction Expansion

From Figure 2,since ratio of b/a～0.996,it follows that

The square root term is introduced to force the starting guess for the satellite ground-track vector to lie on the Earth’s surface defined by Eq.3.Numerical experiments have shown that setting A to an identity matrix yields satellite height errors of～kilometers,whereas setting A to the Earth surface curvature matrix of Eq.3 yields satellite height errors of～m.Since the second option yields 6-7 digits of the satellite height error,this is adopted as the starting guess.After the solution for the satellite ground-track vector has converged,the satellite height and geodetic latitude are computed non-iteratively as

Convergence in the algorithm is checked by introducing Eqs.4,7,and 8 into the loop closure constraint

and checking the convergence criteria

Failure to achieve this goal triggers a new iteration for the algorithm.The basic flow diagram is presented in Figure 3.

Figure 3:Flow diagram for Cartesian to Geodetic Transformation.

4 Numerical Results

Error plots are presented for the initial condition errors for satellite height and geodetic latitude.The second set of plots presents the error plots after the first iteration of the continued fraction calculation.Last,error plots will be presented for the second iteration of the continued fraction.

As shown in Figure 4 for the entire LEO-GEO range the maximum initial satellite height error is～30 m.This provides 6-to-7 digits of the desired solution for the required geodetic height.The initial geodetic anomaly errors are seen to be 2 x 10−3deg.,which provides 3-to-5 digits of the desired solution.The high accuracy of these results significantly impact the performance of the continued fraction expansion iteration.

Figure 5presents the results of the first iteration of the continued fraction expansion.The error in the satellite height has been reduced9 orders of magnitude,with no indication of any problems arising near the poles.The maximum error is～10−8m.,which is accuracy far beyond any data for space applications that can be measured.Similarly,the geodetic anomaly has been reduced6 orders of magnitude,also with no indication of any problems arising near the poles.The angular errors at GEO produce positional errors of～3 mm.It is truly amazing that the continued fraction in the satellite ground-track vector converged in a single iteration for all practical engineering applications.

Figure 5:First iteration of Error Plots for satellite height and geodetic latitude.

Figure 6presents the results for the second iteration of the continued fraction expansion.The satellite error is not seen to improve.This results because the solution for the first iteration is already at the limits of double precision accuracy.The error for the geodetic anomaly is reduced by anadditional 5 orders of magnitude.

Figure 6:Second iteration of Error Plots for satellite height and geodetic latitude.

The proposed algorithm provides solution accuracies for a single iteration that outperform previously reported results for 3rdorder and higher Newton-like iteration algorithms.However,no derivatives or Jacobian partial derivatives are required.Even though a matrix inverse appears in the continued fraction iteration formula,the matrix is diagonal and trivially inverted.Timing tests are performed to compare the run-time performance when compared with other state-of-the-art algorithms.Should higher precision ever be required the most natural approach consists of simply performing extended precision calculations.This is suggested because the satellite height errors appear to have reached the limits of double precision calculations even at the first iteration.The method is elegantly simple;trivial to program;and amazingly effective numerically.

Performance tests are carriedout using Fukushima(2006)as the baseline.Bowring(1976)has been the “gold standard”for all algorithms.Timing tests have been performed,where 106runs using Bowring’s algorithm and the proposed method presented in this paper.Four simulations of this type were performed.The mean of the ratio=Bowring/Fukushima=1.91.The comparison between current methods/Fukushima=1.72 in the run time required.Further boosts in performance can be achieved by mapping the calculations to the Meridonal plane for the Earth’s ellipse.This opportunity will be explored in future research.Other algorithms are slightly faster,because they do not require vector operations.Nevertheless,it is remarkable that simplicity of the proposed algorithm yields convergence performance far exceeding the many other proposed methods,without requiring derivative or Jacobian calculations or higher-order correction terms,without singularities.

5 Conclusions and Recommendations

As shown in the numerical results section the proposed vector-valued continued fraction expansion converges in a single iteration and provides very high accuracy throughout the LEO-GEO range of applications.It is singularity free.It is not the fastest algorithm developed,but it is elegantly simple to formulate and solve.The 3D satellite ground-track vector is used as an unconventional and highly effective solution variable.Future research will investigate the performance impact of mapping the continued fraction expansion to the meridian plane that contains the satellite position vector.

Borkowski,K.(1989):Accurate algorithms to transform geocentric to geodetic coordinates.Journal of Geodesy,vol.63,no.1,pp.50-56.

Bowring,B.R.(1976):Transformation from spatial to geographical coordinates.Survey Review,vol.23,no.181,pp.323-327.

Elgohary,T.;Turner,J.D.(2012):High-Order Analytic Continuation and Numerical Stability Analysis for the Classical Two-Body Problem,Jer-Nan Juang Astrodynamics Symposium,AAS-12-639,College Station,TX,Jun.,2012,pp.627-646.

Feltens,J.(2009):Vector method to compute the Cartesian(X,Y,Z)to geodetic(λ,h,ϕg)transformation on a triaxial ellipsoid.Journal of Geodesy,vol.83,no.2,pp.129-137.

Fotiou,A.(1998):A pair of closed expressions to transform geocentric to geodetic coordinates.Zeitschrift f¨ur Vermessungswesen,vol.123,no.4,pp.133-135.

Fukushima,T.(1990):Fast transform from geocentric to geodetic coordinates.Journal of Geodesy,vol.73,no.11,pp.603-610.

Fukushima,T.(2006):Transformation from Cartesian to Geodetic Coordinates Accelerated by Halley’s Method.Journal of Geodesy,vol.79,no.12,pp.689-693.

Heiskanen,W.A.;Moritz,H.(1967):Physical geodesy.W.H.Freeman,San Francisco.

Hofmann-Wellenhof,B.;Lichtenegger,H.;Collins,J.(1997):Global Positioning System:theory and practice.Springer-Verlag,New York.

Kleusberg,A.;Teunissen,P.J.(1998):GPS for geodesy.Springer,New York.

Lin,K.C.;Wang,J.(1995):Transformation from geocentric to geodetic coordinates using Newton’s iteration.Journal of Geodesy,vol.69,no.4,pp.300-303.

Ligas,M.;Banasik,P.(2011):Conversion between Cartesian and geodetic coordinates on a rotational ellipsoid by solving a system of nonlinear equations.Geodesy and cartography,vol.60,no.2,pp.145-159,2011.

Lupash,L.O.(1985):A new algorithm for the computation of the geodetic coordinates as a function of earth-centered earth-fixed coordinates.Journal of Guidance Control Dynamics,vol.8,pp.787-789.

Petr,V.C.;Anek,P.(1982):Geodesy,the concepts.Elsevier Science Pub.Co.,New York.

Pick,M.;Šimon,Z.(1985):Closed formulae for transformation of the Cartesian coordinate system into a system of geodetic coordinates.Studia Geophysica et Geodaetica,vol.29,no.2,pp.112-119.

Pollard,J.(2002):Iterative vector methods for computing geodetic latitude and height from rectangular coordinates.Journal of Geodesy,vol.76,no.1,pp.36-40.

Strang,G.;Borre,K.(1997):Linear algebra,geodesy,and GPS.Wellesley-Cambridge Press.

Torge,W.(1980):Regional gravimetric geoid calculations in the North Sea test area.Marine Geodesy,vol.3,no.1-4,pp.257-271.

Turner,J.(2009):A non-iterative and non-singular perturbation solution for transforming Cartesian to geodetic coordinates.Journal of Geodesy,vol.83,no.2,pp.139-145.

Turner,J.D.;Junkins,J.L.(2011):Universal Algorithm for Inverting the Cartesian to Geodetic Transformation.Journal of the Astronautical Sciences,vol.58,no.3,pp.429-443.

Turner,J.D.;Elgohary,T.(2013):A simple Perturbation Algorithm for Inverting the Cartesian to geodetic Transformation.Mathematical Problems in Engineering,vol.2013,Article ID 712729,5 pgs,

Turner,J.D.,Elgohary,T.;Majji,M.;Junkins,J.L.(2011):Keynote Paper:High Accuracy trajectory and Uncertainty Propagation Algorithm for Long-Term Asteroid Motion Prediction,Presented to International conference on Computational and Experimental Engineering&Sciences,Nanjing,china,17-21 April 2011.Also published as part of a Festschrift in honor of John L.Junkins Lifetime Achievement Award at the ICCESS:Adventures on the Interface of Mechanics and Control.(Invited),Tech.Science Press,2012,pp.1-14.

Vermeille,H.(2004):Computing geodetic coordinates from geocentric coordinates.Journal of Geodesy,vol.78,no.1,pp.94-95.

Zhang,C.D.;Hsu,H.T.;Wu,X.P.;Li,S.S.;Wang,Q.B.;Chai,H.Z.;Du,L.(2005):An alternative algebraic algorithm to transform Cartesian to geodetic coordinates.Journal of Geodesy,vol.79,no.8,pp.413-420.

1Khalifa University,Abu Dhabi,UAE.