数学分析中关于极限概念的几点教学体会*

黄仁帅

（百色学院，广西百色533000）

数学分析中关于极限概念的几点教学体会*

黄仁帅

（百色学院，广西百色533000）

极限理论是数学分析的基础理论，贯穿数学分析整个学科，在数学分析的理论体系中具有重要地位。在数学分析的教学实践中发现，由于极限概念本身的抽象性，学生对极限概念难以理解。文章就学生在学习极限概念时感到困惑的原因进行分析，并就教师在教学中如何把握极限概念的教学给予一点建议。

数学分析；极限理论；极限概念

数学分析的真正意义上的创立始于17世纪发展形成的微积分学科，但极限理论作为数学分析的基础理论却是到19世纪末才得以完善。极限理论作为数学分析的基础，贯穿于整个数学分析学科。因此，学好极限概念是学习与掌握数学分析的关键。并且，数学分析作为数学专业的一门主干基础课，对学好其他后续课程意义重大，这进一步地突显了学好极限概念的重要作用。

极限概念作为学生学习数学分析时要掌握的第一个重要概念，数学分析中的很多重要概念都是通过极限来定义，如导数定义为差商的极限、数项级数定义为部分和数列的极限、定积分定义为黎曼和的极限等。事实上，以上概念定义的叙述都只需在极限定义叙述的基础上依具体问题稍作修改即可。然而，从数学分析的教学中不难发现，由于极限概念抽象、定义叙述冗长、符号关系复杂，导致学生对极限概念理解模糊，难以掌握。因此，把握好极限概念这一部分的教学对学生学习数学分析具有重大意义，直接关系着学生对数学分析及后续数学相关课程的学习与掌握。文章就学生在学习极限概念时感到困惑的原因进行分析，并就教师在教学中如何把握极限概念的教学给予一点建议。

一、极限概念的精确化历程

极限概念是数学分析中最重要的概念，且是学生学习数学分析第一个要接触的较复杂的概念，故而很多学生都觉得极限概念不好理解，难以弄清极限为何如此定义的缘由。因此，还需让学生对极限的发展历程有一个清晰的认识。

从极限概念的精确化历程来看，由朴素极限思想的萌芽至极限概念的精确化共经历了约两千多年[1]。据已有文献，公元前五世纪开始已经产生了一些朴素极限思想，如古希腊雅典时期形而上学学者Zeno的“神行太保Achilles永远追不上乌龟”悖论和Antiphon为解“化圆为方”问题的穷竭法，中国古代梁国宰相施的“一尺之棰，日取其办，万世不竭”与魏晋时期数学家刘徽的“割圆术”等都涉及了极限的思想。

到了17世纪上半叶，随着自然科学领域的重大突破（行星运动三大定律、自由落体定律、动量定律等），人们迫切需要新的数学工具来解决所面临的新问题，“微积分”应运而生。然而，虽然微积分的诞生和发展在众多领域都取得了丰硕的成果，并引发了世界范围内的一场科学革命，但由于Newton和Leibniz在17世纪下半叶分别建立的微积分缺乏稳固的基础，引发了数学发展史上的第二次危机。

在微积分创立后的一百多年中，由于基础的不牢固，人们在分析问题时得到了许多错误的结论，这使得数学家们认识到必须为分析建立严格的基础。经过众多数学家的努力，尤其是法国数学家Cauchy和德国数学家Weierstrass的突出工作，最终消除了第二次数学危机并从根本上解决了第一次数学危机。Cauchy对微积分的基本概念给出了明确的定义，将导数、积分、级数等都看成是某种极限过程，为分析的严格化迈出了关键的一步。Weierstrass的突出贡献在于为分析的严格化创造了ε-δ语言，使分析从直观的描述性语言中解放出来，并依此建立了实数理论，使得分析的严格化得以最终完成。

二、极限概念的教学

用极限去研究函数是数学分析区别于初等数学的一个显著标志，数学分析中几乎所有的概念都离不开极限。因此，学习数学分析的学生必须学好极限，教数学分析的教师必须教好极限。

从以往的教学情况来看，对于极限的定义[2]：

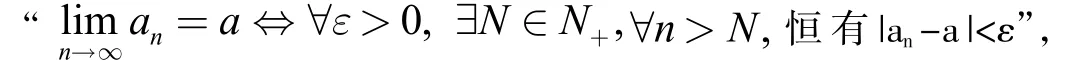
大多学生会有以下两点疑惑：

1.关于正数“ε”。首先，ε具有绝对的任意性，这样才能使得数列{an}无限的趋近于a。另外，ε又具有相对的固定性，这样才能估算an与a的接近程度。正是ε的这种两重性给学生带来了很大的困惑，导致学生不理解Mε（M为正的常数）、等在本质上是一样的，也不理解为什么有时候可以将ε限定在一些较小的范围内

2.关于“∃N∈N+”。一方面，正整数N是通过解不等式“|an-a|＜ε”来确定的，即N的值跟ε有关。另一方面，正整数N并不是唯一的，它并不是关于ε的函数。这种跟ε“若即若离”的模糊感，使得许多学生不敢轻易确定正整数N的取值。再者，由于常常将N看成是一个充分大的正整数，故而很多时候在证明的开始就限定了N要大于某些正数，如N≥7或N＞9等，这进一步使得学生对极限概念的逻辑结构的理解混乱不清。

针对上述两点，要求教师在讲授极限概念时必须反复强调以下两点：

1.关于正数“ε”，必须强调ε在给定之前是任意的，并且应该是较小的一个正数，但在给定之后就是一个常数。ε的绝对任意性是通过无限多个相对固定性来进行刻画的，是一个运动的无限过程，不能用静止、不变的观点来进行分析。

2.关于“∃N∈N+”，强调N的是由相对固定的ε代入不等式“|an-a|＜ε”求解得到。接着，由于ε绝对任意性，N的取值又随ε的变化而变化。但是，由于N的不唯一性，所以不能说N是ε的一个函数，只是说跟ε有关而已。

为加深学生对上述两点的理解，在教学中除了采用讲授、讨论、练习相结合的方式外，还可以通过Matlab软件的画图功能对一些数列的极限过程进行动态演示，引起学生的学习兴趣。

然后通按回车键，可再现数列{an}随n的变化所生成的点列的图形，最终得到的图形如图1。要想观察数列{bn}散点图，只需将程序中的“an=sin（10./n+pi/2）”改写成“bn=sin（20./ n+pi/2）”，然后重复上述操作即可得图2。

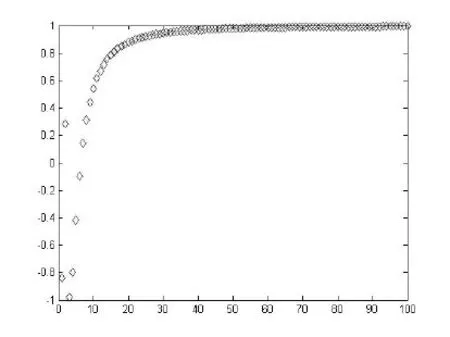
图1　数列{an}的图像

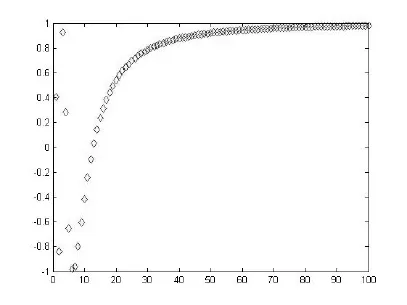
图2　数列{bn}图像

可以看到，虽然两个图像步调不太一致，但随着n变得越来越大，两个数列最后都趋向于1。

通过这样的方式，不仅让抽象的极限概念用图形直观的表现出来，也利于培养学生的学习兴趣和学以致用的意识，使课堂变得更有趣。

三、结束语

极限概念作为数学分析的第一个重要概念，教师必须把握好这一概念的教学。从多个角度入手进行分析讲解，将极限概念中各个量的抽象关系理清楚，并给学生以直观的展示。

[1]马知恩，王绵森.高等数学疑难问题选讲[M].北京：高等教育出版社，2014.

[2]刘玉琏，傅沛仁.数学分析讲义[M].北京：高等教育出版社，2008.

[3]胡良剑，孙晓君.MATLAB数学实验[M].北京：高等教育出版社，2006.

The limit theory is the basis of mathematical analysis,which runs through the whole course of mathematics analysis,and plays an important role in the theoretical system of mathematical analysis.In the teaching practice,it is found that students cannot understand the concept of limit because of the abstract nature of the limit concept itself.This paper makes an analysis of the reasons why students feel confused in the concept of learning limit,and gives some advice on how to grasp the concept of limit in teaching.

mathematical analysis;limit theory;limit concept

O171

A

2096-000X（2016）24-0120-02

广西高校中青年教师基础能力提升项目（KY2016LX354）；百色学院校级教育教学改革工程项目（2016JG54）

黄仁帅（1987-），男，广西贺州人，百色学院教师，研究方向：数学与应用数学。