量子拜占庭协议中的纠缠态探测

武霞，贾恒越，朱建明

（中央财经大学信息学院，北京 100081）

量子拜占庭协议中的纠缠态探测

武霞，贾恒越，朱建明

（中央财经大学信息学院，北京 100081）

在分布式计算系统中，拜占庭协议是解决其容错问题的一种实用方法。拜占庭问题有一种演变形式，称之为检测的拜占庭协议。这类协议在经典世界中无法解决容错问题，但在量子系统中利用纠缠态却可以。GBKCW协议是一种典型的量子检测拜占庭协议。针对GBKCW协议中数据列表的生成和分发部分，利用量子纠缠态的确定性，探测了参与者共享的量子态，以抵御针对GBKCW的截获重发攻击。

检测的拜占庭协议；GBKCW协议；量子系统；纠缠态的确定性

1 引言

在分布式计算系统中，只有每一个组件都协调合作，整个系统才能正常运行。但现实生活中，分布式系统的某些组件出现问题的情况难以避免，如有问题的组件可能发送无效或错误的信息给系统中其他的组件。如果这种情况发生，那么将威胁系统的正常运作。而拜占庭协议[1,2]就是一种解决分布式系统容错问题的实用的方法。

详细地说，最简单的拜占庭问题具体可被描述如下[3]。有3路拜占庭军队，分散驻扎于敌军城外，其中每一支军队都有一个将军，称他们为A、B、C。将军们彼此之间可以通信来传递消息，他们想通过传递消息来达成一致的行动计划，即攻击或撤退。指挥官将军A决定了一个计划，并且将他的计划发送给了B和C，接下来B和C交换他

们手中收到的消息，来保证行动计划的一致性。然而在他们中可能有将军已经被敌军收买，变成了叛徒（包括指挥官 A），他试图阻止所有诚实的将军们达成一致的行动计划。拜占庭问题是指设计满足下面2个条件的协议：1) 所有诚实的将军们执行同一个计划；2) 如果指挥官将军A是诚实的，那么所有诚实的将军都遵守A所制定的行动计划。

3个将军的拜占庭问题是无解的[4,5]，除非将军们事先分享某些合适的私人数据。即每个将军必须拥有不为其他将军所知的数字列表，但这个数字列表还要与其他将军的数字列表有适当的关联关系。因此解决拜占庭问题可以简化为解决生成和安全分发这些列表的问题。然而，无论在经典世界还是量子世界中，都没有方法来保证所需要的数字列表分发成功。然而3个将军的拜占庭问题可以产生一类演化问题，称之为检测的拜占庭协议或者检测广播[3,6～14]，这种条件放松后的拜占庭协议，利用经典方法无法解决，但是利用量子资源——量子纠缠态却可以。在检测的拜占庭协议中，条件 1)和 2)放松为：1') 所有诚实的将军要么执行相同的计划，要么终止行动；2') 如果A是诚实的，那么每个诚实的将军要么遵守A所制定的计划，要么终止行动。而达成这个协议，所依赖的就是量子世界所独有的性质。

众所周知，量子力学是20世纪物理学中最伟大的进展之一[15,16]，它能够解释许多经典物理所不能解释的现象[17]。量子系统中，存在一种被我们所熟知的量子态，即量子纠缠态[18]。量子力学不同于经典物理，最神奇的特征就是量子纠缠，纠缠反映了量子理论的本质。而与经典信息论中的信息资源截然不同的是，纠缠是一种崭新的量子资源，一些利用经典手段所不能实现的任务却可以利用纠缠来实现。因此利用量子纠缠可以实现许多令人惊叹的应用，如单向量子计算[19,20]、量子密钥分发[21,22]、量子隐形传态[23]。本文介绍的检测拜占庭协议，也是量子纠缠态的一次非常完美的应用。

一般的量子检测的拜占庭协议包括 2个部分。第一部分主要给3个将军生成和分配数据列表，在这一部分中主要利用的就是量子纠缠态特殊的性质。这一部分最重要的是检测纠缠态，即3个将军采取适当的方法，来确认他们之间分配的量子纠缠态是协议第二部分中所用到的那个态。第二部分是协议的主体部分，一旦3个将军拥有了各自的数字列表，在协议的第二部分中，他们利用这些数字列表，并结合双向经典通信来达成一致行动。

由此可见，分发和检测量子态在量子检测拜占庭协议中至关重要，本文提出一种新的检测拜占庭协议中量子态的方法，即利用量子纠缠态的确定性。

量子纠缠态的确定性问题，是量子纠缠理论研究中最重要的问题之一[24～29]。在这个问题中，人们主要研究量子纠缠态与其子系统的约化密度矩阵之间的关联性质。简而言之，对几乎所有的量子态，它们都可以由其约化密度矩阵唯一确定。本文利用三体纠缠态可以由其两体约化密度矩阵所唯一确定的性质，来讨论GBKCW协议第一部分有关量子态探测的问题。

2 准备知识

2.1 拜占庭将军问题

分布式计算的一个基本目标是：即使在某些分布式进程失败的情况下，分布式计算依旧能够进行。这要求无故障组件在收到受干扰信息的时候依旧能够达成一个一致性协议。解决这样任务的问题被简称为拜占庭将军问题，也称为拜占庭协议。拜占庭协议简要描述如下。

有3路拜占庭军队包围了一座敌军城市，每一路军队都由一个将军带领，分别为A、B、C。将军只能通过消息进行相互通信（通过双方认证无错经典信道）。通过消息通信，将军们必须决定一个一致的计划：攻击，用0表示；撤退，用1来表示。指挥官将军A决定了一个计划，并且将他的计划传递给将军B和C，传递给将军B的消息记为ABm ，传递给将军C的消息记为ACm 。接下来，B将其消息BCm 传递给 C来进行行动计划的沟通，C也将消息CBm 传递给将军B。然而，其中一个（有且仅有一个）将军（包括 A）有可能是叛徒，试图阻止诚实的将军们达成同一个计划。对于诚实的将军C来说，会出现下面2种情况。

1) 将军B是叛徒。指挥官A发给将军B和C同样的消息， mAB= mAC=1。B收到消息后为了干扰将军C，他将A传来的消息进行了修改，因此他传递给C的消息是 mBC= 0，而C传递给B的消息是正确的，即 mCB= mAC=1。在这种情况下，可以看出将军C收到了2个互相矛盾的消息，0和1。

2) 指挥官A是叛徒，他发送给B的消息为mAB=0，发送给C的是 mAC=1。因为只能有一个叛徒，此时将军B和C都是诚实的，B把从A那里收到的消息发送给C，mBC= mAB=0，C传递给B的消息为 mCB= mAC=1。在这种情况下，将军C又收到2个互相矛盾的消息，0和1。

众所周知，解决拜占庭问题可以简化为解决生成和安全分发数字列表的问题，而根据量子力学的性质，人们已经提出了多种生成和安全分发所需数字列表的方法。迄今为止，这些方法有的基于三体三维单重量子态[3]，有的基于四量子比特纠缠态[6,7,9]，有的基于3个或者2个量子密钥分发信道[12]，有的利用单体三维量子态[10]，还有的利用Hardy争论问题[11]。Hardy争论反证了量子关联的一种局域隐变量描述，它是没有不等式的Bell理论的一种形式。

本文主要讨论的是GBKCW协议中四量子比特纠缠态的一种新颖的探测方法，即利用纠缠态的确定性。

2.2 量子纠缠态的确定性

量子纠缠理论主要研究纠缠的数学结构，及其刻画、操纵和度量。人们试图从很多视角来理解多体量子纠缠态，其中的一种方法就是将纠缠看成是整个量子态与其子系统之间的关联，即从部分和整体的角度来看待量子纠缠。人们也称之为量子纠缠态的确定性。

详细地说，给定多体量子纯态的一部分，其中，部分是指子系统的约化密度矩阵，那么，从部分中能够获得关于整个量子态什么样的信息？这就是量子纠缠态的确定性问题。

在量子纠缠态的确定性问题中，想要计算一个给定的n体量子态ψ，到底可以被其几体约化密度矩阵的集合所唯一确定。给定一个n体量子态ψ，很容易可以求出它的任意约化密度矩阵，不妨设ψ的所有约化密度矩阵的集合为R，但是如果已知的是约化密度矩阵的子集R ′⊂ R，那么是不是还有其他的量子态ψ′，其相应约化密度矩阵集合跟R′一致？如果存在这样其他的量子态，那么称ψ不能被R′所唯一确定；反之，则称ψ由R′所唯一确定，并且R′称为ψ的确定集。

由于这个问题的解决与探究纠缠有密切的关系，因此近10年来获得了很多关注，并且取得了一些很好的结论。

对GBKCW协议中所描述的3个将军的量子检测拜占庭协议，至关重要的一步是3个将军探测他们之间共享的到底是不是某个特定的四粒子纠缠态。而通过将军之间彼此将其拥有的量子比特传递给对方，然后检测手中所具有的新的二体量子态，最后与四粒子纠缠态相应二体量子态进行对比的方法，提供一种新颖的量子态探测方式。在这之前，需要首先回忆GBKCW协议中探测的拜占庭协议的第二部分，然后再分析协议第一部分中纠缠态的探测问题。

3 检测的拜占庭协议

拜占庭问题已经被证明是不可解决的问题，除非每个将军都有不被其他将军所知的数字列表，并且自己拥有的数字列表与其他将军手中的列表之间有合适的关联关系。因此，解决拜占庭问题可以简化为解决生成和安全分发这些列表的

问题。利用量子协议就能检测分发的安全性，然而，一旦有了攻击，就没有可用的秘密列表，并且整个通信必须终止。在这种情况下，拜占庭协议有一种演变形式，称之为检测的拜占庭或检测广播。在检测的拜占庭协议中，需要满足下面 2个新的条件：1')所有诚实的将军要么执行相同的计划，要么终止行动；2')如果A是诚实的，那么每个诚实的将军要么遵守A所指定的计划，要么终止行动。这个协议在经典世界是不能完成的，在量子领域却可以。而达成这个协议，所依赖的就是量子世界所独有的性质。

GBKCW协议中，检测的拜占庭协议分为2个部分。第一部分的目标是利用一种特殊的四量子比特纠缠态的相关性质，生成并且分发3个数据列表，其中，A手中的列表记为Al，B、C手中的数据列表分别为Bl和Bl。一旦将军们手中有了这些列表，在协议的第二部分，他们利用这些列表和双向经典通信来完成协议，达成一致的计划或检测出说谎者。

详细地说，列表Al、Bl和Cl具有下面的性质。

性质1 3个列表长度相等。Al中的元素是集合{0,1,2}的任意一个元素。Bl和Cl的元素在比特0,1中任意选取。

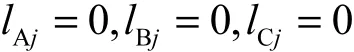
性质 3 除了能从自己的列表中根据性质 1和性质2所推断出的，每个将军都不知道其他将军的列表内容。

例如，如果将军A发现自己手中第j位的元素是0，即lAj= 0，那么根据3个将军之间列表的性质，他可以推断出将军B、C相应位置上的元素也必定是 0。而如果 lAj= 2，此时他推断不出B、C位置上的元素。对于将军B来说，如果他发现lBj= 0，那么他只能推断出lAj= 0或lAj= 2，而 lCj等于0或1。即此时他也无法判断别的将军手中的粒子是几。

为了简化协议第二部分的讨论，本文只站在C的角度来分析，因为B和C的角色是完全对称的，因此本文对于将军C出现的情况，完全适用于B，反之亦然。

协议部分如下。

1) 当指挥官A发送消息ABm （0或1）时，随之一起发送的还包括其他的数据，这个数据必须与消息本身有关，并且只为A所知。为了达成这个目的，A同样发送一个数据列表ABl给B，这个列表中包含Al中出现比特ABm 的所有位置。之后如果A诚实，他会遵守自己发送的计划。

举例来说，假设

A要发送消息0。如果指挥官A诚实，那么他会发送 mAB= mAC= 0，同时发送lAB= lAC= {2,3,8,10}。

当B收到 mAB和 lAB，只会产生2个结果。

①若 lAB的长度合适（根据性质1，可知 lAB长度大约是数据列表l的1），并且 m 、l 和l确

A3ABABB实满足性质2，那么此时称数据（即 mAB、 lAB和lB）一致。如果数据一致，那么B将服从计划 mAB，除非在协议的下一步2)中，将军C使他相信A是叛徒。

例如，将军B收到 mAB= 0,lAB= {2,3,8,10}，他首先发现 lAB的长度合适，为4。接下来检查lB中的比特在位置 lAB上确实都为0，此时数据一致。

②若 mAB、lAB和lB不一致，那么B确认A是叛徒。B将不采取任何行动，直到在协议的下一步与C达成一致的计划。

例如，B收到 mAB= 0，lAB= {2,3,7,10}，此时数据不一致。因为A在位置7不可能为0。

2) B将自己收到的数据传递给C。消息BCm 不仅可以为0或者1，还可以为“⊥”，表示“我收到了不一致的数据”。而如果B收到的消息为0或者1，他发送给C其他的数据来表明BCAB=m m 。为了这个目的，B同样发送一个列表BCl给C，并且声称这与从A处收到的ABl一样。

当C收到来自B的BCm 、BCl或者“⊥”，他手头早已收到来自A的ACm 和ACl。接下来，罗列在C手中的信息到底会出现多少种可能。

对于来自A的信息，只有2种可能情况。

①A1：ACm 、ACl、Cl一致。

②A2：ACm 、ACl、Cl不一致，即“⊥”。

对于来自B的信息，有以下4种情况。

①B1： mBC、lBC、lC一致，且 mBC= mAC。

②B2： mBC、lBC、lC一致，且 mBC≠ mAC。

③B3：“⊥”，即B告诉C，他已经知道A是叛徒。

④B4：BCm 、BCl、Cl不一致。

下面对以上情况进行排列组合。

如果C手中的信息是A1B1，此时没有叛徒，3个将军达成了相同的行动计划，C服从计划mAC=mBC。

如果C手中的信息是A1B2，那么C可以断定指挥官A是叛徒，他只需执行事先与B商定好的行动计划。这是因为A是唯一能够发送一致数据给B和C的人。

如果C手中的信息是A1B3，那么C服从计划ACm 。在这种情况下，B并没有任何办法说服C，他从A处确实收到了不一致的信息。

如果C手中的信息是A1B4，那么C确认B为叛徒，他执行计划ACm 。这是因为C没有收到“⊥”，这说明在B手中ABm 、ABl和Bl一致。如果B诚实，他必定发送 mBC= mAB,lBC= lAB到C处，此时BCm 、BCl 、Cl必定也一致。

如果C手中的信息是A2B1或A2B2，此时A是叛徒，他们服从计划BCm 。

如果C手中的信息是A2B3，那么B和C都知道A是叛徒，他们只需执行事先定好的计划。

C手中的信息是A2B4这种情况，是不可能出现的。

这就是GBKCW协议的第二部分。而要执行这个协议的前提，就是数据列表的分发。在GBKCW协议中，给出了数据列表的生成和分发方法，但是存在很严重的漏洞，并且很快被Gao等[6]利用截获—重发攻击所击破。在GBKCW协议给出的数据列表的分发方法中，利用截获重发攻击，叛徒能够控制接下来协议的整个第二部分，他可以达到完美的欺骗，而不被另外2个将军所察觉。

4 利用态的确定性方法探测纠缠态

在GBKCW协议的第一部分，是生成和分发具有性质1、性质2、性质3的数据列表。他所做的步骤是：首先有一个粒子源S制备并分发一类特殊的四量子比特纠缠态ψabcd，前2个粒子给将军A，后2个粒子分别给B和C；之后A、B、 C在4个粒子上分别做投影测量，如果都用相同的基进行测量，那么测量结果之间展现了性质1、性质2、性质3所需要的完美的关联关系；最后，3个将军检测他们的测量结果是否展现了所要求的关联关系。

但这个协议有一个很大的漏洞。Gao等[6]提出，利用截获—重发攻击，不诚实的将军只需派2个手下截获—测量并重新将粒子源S发送给另外2个将军的粒子，那么不诚实的将军就很容易控制协议的第二部分。他可以在第二部分中的拜占庭协议中，很容易地达成完美欺骗，并且不为另外2个诚实的将军所察觉。

可以看到，叛徒能够这样做的根本原因是，2个诚实的将军并不知道从粒子源S手中收到的粒子已经被进行了操作，他们以为自己手中拿到的粒子依旧是ψabcd中的粒子，而不知道中途已经被人测量并重发过，即已经发生了改变。

为了抵抗这种攻击，可以在将军们收到S发来的粒子后、做投影测量之前，加上额外的一步，即探测3个将军之间的态依旧是ψabcd，没有被进行任何破坏。为了达到这个目的，利用量子纠缠态的确定性方法。

4.1 四粒子纠缠态的确定集

在给出定理之前，先介绍密度矩阵的一些性质。如果n量子比特密度矩阵 ρM=(rij)n×n，那么有下面的性质成立。

① rii≥ 0,∀i。

②如果某个 rkk=0，那么 rik= rkj=0,∀ i, j 。

④ ρM所有的主子式的行列式值都是非负的。

证明 根据约化密度矩阵的计算公式，由

只需证明：对任意一个四粒子量子态（可能是混合态，也可能是纯态）

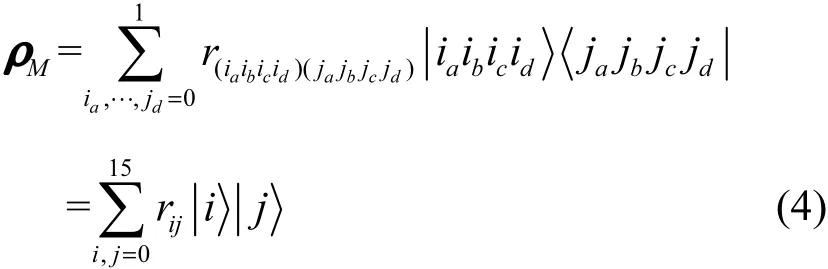
那么ρM=ψψabcd。式(4)中第一个等式是密度矩阵的通俗写法，但为了接下来表达方便，本文将其在第二个等式中用十进制数进行了重新表示，如量子态ψabcd的十进制表示为

这2种表示方法完全等价。

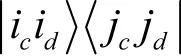
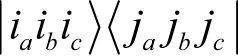
素为

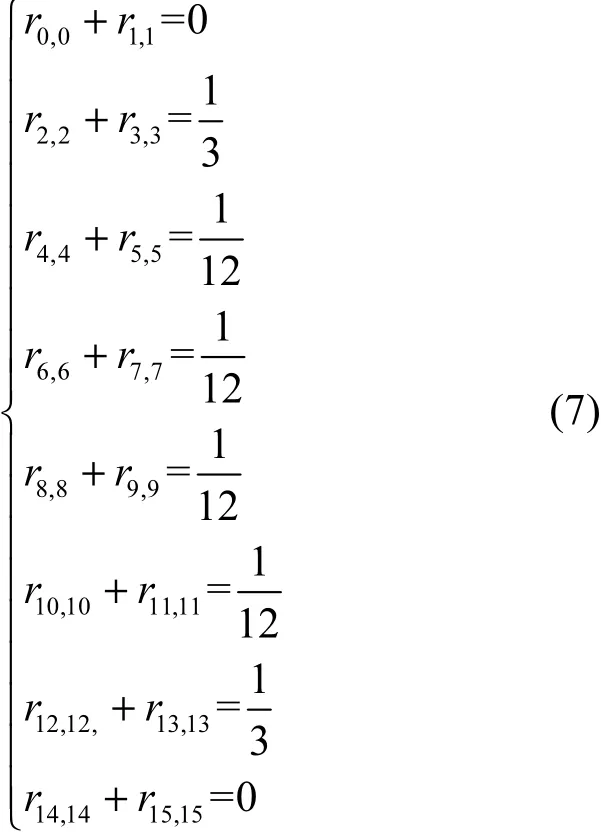
由rii≥ 0可得， r0,0=r1,1=r14,14=r15,15=0。

利用密度矩阵的性质③，式(8)中最后的公式可变换为

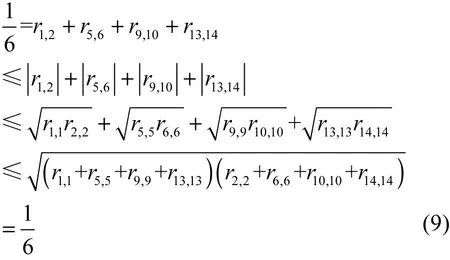
由此可以看出，式(9)中所有的不等式都应该是等式，因此

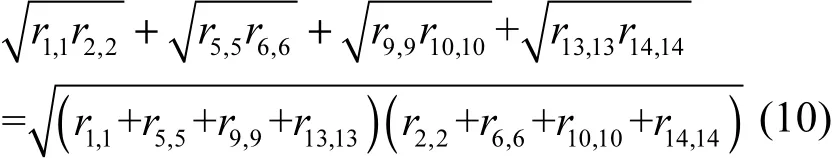
对式(10)进行化简，可以得出

因为 r11= 0，所以从式(11)中可以得出：r2,2=0或者r5,5=r9,9=r13,13=0。而后面的情况不可能成立。这是因为如果 r5,5=r9,9=r13,13=0，那么就有r1,1+ r5,5+ r9,9+ r13,13=0，这与式(8)中的第3个等式矛盾，因此可以得到 r2,2=0。同理因为 r14,14=0，可得 r13,13=0。将这些结果代入式(7)和式(8)中，可以得到 ρM中的对角线元素为

由密度矩阵的性质②可以得到：对任意i′∈ {0,1,2,4,7,8,11,13,14}和任意j，都有ri′j= rji′= 0。接下来，只需证明对于任意 i, j∈{3,5,6,9, 10,12}，都有 rij等于ψψabcd中i j项的系数。

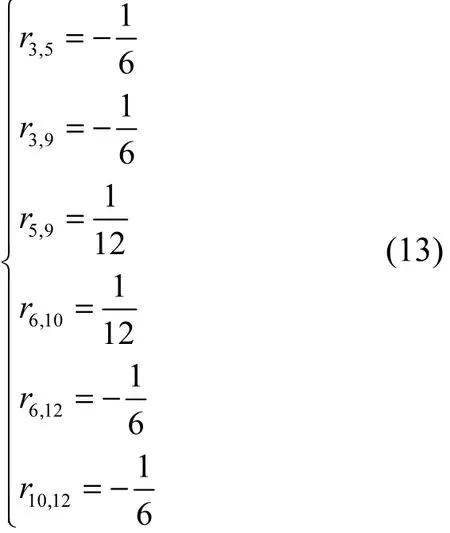
由式(9)得

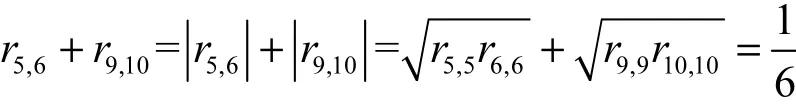
本文的证明还没有结束，因为到这一步为止，还有很多非对角元的值是未知的，如 r3,6,r3,10,…,r9,12等非对角元，迄今为止仍然没有出现过。下面以求 r3,6为例，说明这一类非对角元的求解方法。在这里，本文利用密度矩阵的性质④，考虑 ρM中第3、5、6行和列组成的主子式

以此类推，可以得到，对于任意 i, j∈{3,5,6, 9,10,12}，都有 rij等于ψψabcd中i j项的系数，所以ρM=ψψabcd。

证毕。

需要注意的是，因为粒子c和粒子d的角色完全相同，所以很容易看出=。

对于下面的定理2，证明方法与定理1完全类似，在此不再赘述。

4.2 四粒子纠缠态的探测

在这一步中，本文将GBKCW协议的第一部分协议过程进行一些补充，这个补充就是关于ψabcd态的探测，以确保他们在收到光子源发送的光子之后，他们之间的态并没有被破坏，即没有被截获并操作。

2) A检测自己手中的粒子在态上，而B和C检测他们手中的粒子在最大混合态上。如果成功，继续下一步。

3) 他们 3个分别将自己手中粒子的样本发送给另外2个将军，那么对将军A来说，他手中有2个三粒子态。他探测这2个态是否相等，并且都为。如果成功，根据定理 2，他可以确定3个将军之间分享的确实是量子态ψabcd，并且记为1，否则记为0。对于将军B，他检测手中的二粒子态和三粒子态分别为、，如果检测成功，根据定理1，他确定3个人之间分享的是ψabcd，对于将军C，与B完全等价。

4) 每个将军把自己手中的探测结果发送给另外2个将军。对于诚实的将军来说，如果他手中的结果是1，而他收到的消息中有0，那么发送消息0的将军必定是叛徒。同理，如果他手中结果是0，而他收到的消息中有1，那么发送1的将军必定是叛徒。

5) 如果3个将军手中都是1，并且收到的消息也都是 1，那么他们可以进行接下来的步骤，即数据列表的生成。

从以上可以看出，通过加入量子态的检测步骤，将军之间能够确定他们之间分享是正确的、没有被干扰过的量子态ψabcd。而使这一步成功的基本因素，就是三体量子态ψabcd由其任意的2个两体约化密度矩阵所唯一确定的性质。这是量子纠缠态确定性的一个巧妙的应用。

5 结束语

纠缠作为一种崭新的的量子资源，可以实现很多经典无法实现的任务。它是量子信息处理主要的研究和应用对象。纠缠最为人所知的应用就是量子密码和能够有效分解大数的Shor算法。本文主要研究拜占庭问题的一种演变形式，即检测的拜占庭协议问题。这一类拜占庭问题被证明在经典世界中是无法解决的，但是利用量子方法却可以。

GBKCW协议是一类典型的检测的拜占庭协议。为了抵御针对GBKCW协议的截获重发攻击，本文利用了量子纠缠态由其子系统所唯一确定的性质，在GBKCW协议中数据列表的生成和分发部分，加入了一个新的探测协议。根据量子态的确定性，利用本文提出的方法，可以探测将军们之间共享的是正确的量子纠缠态。这是量子纠缠态的确定性在量子协议中一种全新的应用。本文量子纠缠态由其子系统所唯一确定的性质可以成为一种普遍的探测量子纠缠态的方法。

[1] FITZI M. Generalized communication and security models in Byzantine agreement[D]. Swiss: Swiss Federal Institute of Technology, 2002.

[2] CONSIDINE J, FITZI M, FRANKLIN M, et al. Byzantine agreement given partial broadcast[J]. Journal of Cryptology, 2005, 18 (3): 191-217.

[3] FITZI M, GISIN N, MAURER U. Quantum solution to the Byzantine agreement problem[J]. Phys Rev Lett, 2001, 87 (21).

[4] PEASE M, SHOSTAK R, LAMPORT L. Reaching agreement in the presence of faults[J]. Journal of the ACM (JACM), 1980, 27(2): 228-234.

[5] LAMPORT L, SHOSTAK R, PEASE M. The Byzantine generals problem[J]. ACM Transactions on Programming Languages and Systems (TOPLAS), 1982, 4(3): 382-401.

[6] GAO F, GUO F Z, WEN Q Y, et al. Comment on experimental demonstration of a quantum protocol for Byzantine agreement and liar detection[J]. Phys Rev Lett, 2008, 101 (20).

[7] GAERTNER S, BOURENNANE M, KURTSIEFER C, et al. Experimental demonstration of a quantum protocol for Byzantine agreement and liar detection[J]. Phys Rev Lett, 2008, 100(7): 67-75..

[8] CHIEN C H, LIN T S, LU M Y, et al. Quantum circuit and Byzantine Generals problem[C]//The 12th IEEE International Conference on Nanotechnology (IEEE-NANO).2012.

[9] GAERTNER S, BOURENNANE M, KURTSIEFER C, et al. Addendum to experimental demonstration of a quantum protocol for Byzantine agreement and liar detection[J]. Physics, 2008.

[10] CABELLO A. Solving the liar detection problem using the four-qubit singlet state[J]. Physical Review A, 2003: 68 (1).

[11] RAHAMAN R, WIESNIAK M, ZUKOWSKI M. Quantum Byzantine agreement via Hardy correlations and entanglement swapping[J]. Physical Review A, 2015, 92 (4).

[12] IBLISDIR S, GISIN N. Byzantine agreement with two quantum-key-distribution setups[J]. Physical Review A, 2004, 70 (3).

[13] BOURENNANE M, CABELLO A, ZUKOWSKI M. Quantum Byzantine agreement with a Single Qutrit[J]. Physics, 2010.

[14] SAKURAI J J, NAPOLITANO J. Modern quantum mechanics[M]. Addison-Wesley,2011.

[15] PEREA A. Quantum theory: concepts and methods[J]. Springer Science &Business Media, 2006.

[16] HARDY L. Quantum mechanics, local realistic theories, and lorentz-invariant realistic theories[J]. Phys Rev Lett, 1992, 68(20): 2981-2984.

[17] HORODECKI R, HORODECKI P, HORODECKI M, et al. Quantum entanglement[J]. Reviews of modern physics, 2009, 81(2), 865.

[18] BRIEGEL H J, BROWNE D E, DUR W, et al. Measurement-based quantum computation[J]. Nature Physics, 2009, 5 (1): 19-26.

[19] RAUSSENDORF R, BRIEGEL H J. A one-way quantum computer[J]. Physical Review Letters, 2001, 86 (22), 5188.

[20] SHOR P W, PRESKILL J. Simple proof of security of the BB84 quantum key distribution protocol[J]. Physical Review Letters, 2000, 85(2):441.

[21] CURTY M, LEWENSTEIN M, LUTKENHAUS N. Entanglement as a precondition for secure quantum key distribution[J]. Physical Review Letters, 2004, 92 (21).

[22] RIGOLIN G. Quantum teleportation of an arbitrary two-qubit state and its relation to multipartite entanglement[J]. Physical Review A, 2005, 72(3): 309-315.

[23] LINDEN N, POPESCU S, WOOTTERS W. Almost every pure state of three qubits is completely determined by its two-particle reduced density matrices[J]. Physical Review Letters, 2002, 89 (20), 207901.

[24] LINDEN N, WOOTTERS W. The parts determine the whole in a generic pure quantum state[J]. Physical Review Letters, 2002, 89(27), 131-142.

[25] JONES N S, LINDEN N. Parts of quantum states[J]. Physical Review A, 2005, 71 (1).

[26] PARASHAR P, RANA S. N-qubit W states are determined by their bipartite marginals[J]. Physical Review A, 2009, 80 (1).

[27] WALCK S N, LYONS D W. Only n-qubit greenberger-hornezeilinger states contain n-partite information[J]. Physical Review A, 2009, 79 (3).

[28] RANA S, PARASHAR P. Optimal reducibility of all W states equivalent under stochastic local operations and classical communication[J]. Physical Review A, 2011, 84 (5).

武霞（1987-），女，山东临沂人，中央财经大学讲师，主要研究方向为量子信息。

贾恒越（1983-），女，内蒙古海拉尔人，中央财经大学讲师，主要研究方向为量子信息、量子密码协议设计。

朱建明（1965-），男，山西太原人，中央财经大学教授、博士生导师，主要研究方向为信息安全、经济信息分析。

Entangled state testing in the quantum Byzantine agreement

WU Xia, JIA Heng-yue, ZHU Jian-ming
(School of Information, Central University of Finance and Economics, Beijing 100081,China)

In distributed computing, Byzantine agreement is a practical method to solve its fault-tolerance problem. There is a variation of the Byzantine agreement which is called detectable Byzantine agreement. This kind of protocol is unsolvable by classical means, but can be solved using quantum resources——quantum entangled states. A typical quantum detectable Byzantine agreement is the GBKCW protocol. The part with the generation and distribution of the lists in the GBKCW protocol was dealed with. In order to keep the GBKCW protocol from the intercept-and-resend strategy, the property of the determination of entangled states were employed to test the sharing state between the parties.

detectable Byzantine agreement, GBKCW protocol,quantum system,determination of entangled states

TP309.7

A

10.11959/j.issn.2096-109x.2016.00110

2016-09-24；

2016-10-09。通信作者：武霞，wuxiaqingdao@163.com

国家自然科学基金资助项目（No.61309029, No.U1509214, No.61272398）；中央财经大学青年教师发展基金资助项目（No.QJJ1633）

Foundation Items: The National Natural Science Foundation of China (No.61309029, No.U1509214, No.61272398),The Young Teachers Development Fund of Central University of Finance and Economics (No.QJJ1633)