基于节点亲密度挖掘的谣言抑制算法

田亚平，杨力，王小琴，乔雅峰

（西安电子科技大学网络与信息安全学院，陕西 西安 710071）

基于节点亲密度挖掘的谣言抑制算法

田亚平，杨力，王小琴，乔雅峰

（西安电子科技大学网络与信息安全学院，陕西 西安 710071）

通过对谣言等易误导大众舆论的信息传播进行抑制，从而实现对谣言、错误舆论等负面信息的控制。首先，通过对社交网络的结构拓扑以及节点行为特点的分析，提出了基于节点亲密度的社交网络舆论领袖节点识别方法；然后，利用谣言传播特性及节点的亲密度，建立谣言传播模型，并分析谣言在社交网络中传播时节点的状态转化过程；最后，提出了一种利用节点亲密度实现谣言抑制的方法。

谣言传播模型；亲密度；社交网络；谣言抑制

1 引言

近年来，随着科技的进步以及互联网技术的发展，社交网络得到了迅速的发展。无论是在国内还是国外，社交网络都拥有数亿的用户量，如新浪微博、Facebook等。社交网络为广大的用户提供了一个信息分享和沟通的平台，极大地满足了人们的社交需求，已不再是一个纯粹虚拟的社会，而是与现实社会密不可分。越来越多的人喜欢在社交平台上交流互动，同时也热衷于从社交平台中获取信息并进行转发评论。而这些信息中，一些未经求证的谣言泛滥成灾，因此而造成的恶意事件也逐渐增多，影响和干扰着人们正常的生活秩序。谣言在社交网络中的肆意传播，严重影响到社会稳定、经济发展，有效地控制社交网络中信息的传播

具有重要意义。

本文首先通过对社交网络中结构拓扑以及节点的行为特征进行分析讨论，得到信息传播过程中存在的“熟人效应”现象[1,2]，通过节点亲密度实现对网络中的舆论领袖节点进行识别。然后，分析了谣言传播模型，以及谣言在社交网络中传播时节点的状态转化过程。最后，提出了一种基于亲密度的谣言抑制方案。

2 舆论领袖节点的识别

社交网络中谣言的散播一般具有普遍性，可以引起群体大众在思想上的某种共鸣；为吸引大众的关注，散布者有意地夸大某种事实，满足人群的猎奇心理；同时具有一定的模糊性，使谣言不易被识破，无法短时间判断信息的真实性。Soh等[3]提出在多变的动态环境影响下，网络中节点间的连接矩阵是随着时间而动态变化的，并进一步分析了在动态网络中谣言的传播；Panagiotou等[4]提出具有不同拓扑结构的社交网络、谣言传播的特点；Acan等[5]提出了对于谣言推动和挽回策略；Fountoulakis等[6]提出随机网络中网络密度对于信息广播传播的影响；Giakkoupi[7]和Chierichetti等[8]对于谣言传播过程中传播范围进行了进一步细致的分析。

社交网络中谣言传播的控制一直是一个关键性的问题，也是一个难点。在现存的解决方法中主要分为两类措施[9]：1) 积极措施，包括通过控制社交网络中的节点，从而实现对谣言传播的阻塞作用；2) 亡羊补牢型措施，通过社交网络中注入与谣言相对的真实信息实现对谣言的澄清，当人们先后接收到2种相对的信息时，降低了谣言的可信度，达到亡羊补牢的效果。社交网络一般具有用户基数大的特点，通过控制所有的节点从而达到对于谣言传播的阻塞是不可能实现的，所以需要识别出社交网络在信息传播过程中起关键作用的舆论领袖节点。

2.1 度中心性

节点的重要性只考虑了一个节点参与网络的总水平而没有考虑与其相连的邻居节点所具有的重要性对其影响的数量，可认为是节点中邻居节点的数目，如式(1)所示[10]。

其中，i表示网络中的一个节点，j表示网络中所有其他的节点，N为所有的节点总数，x表示邻接矩阵，若ijx的值为1，则表示节点i与节点j之间存在一条连边；否则值为0。

2.2 紧密度中心性

紧密度中心性[11]的测量方法依赖于网络中通过某节点的最短路径的长度。在网络分析的过程中，若使用紧密度中心性作为节点重要程度的衡量标准则，表示距离其他节点越近的节点有越高的紧密度中心性，如式(2)所示。

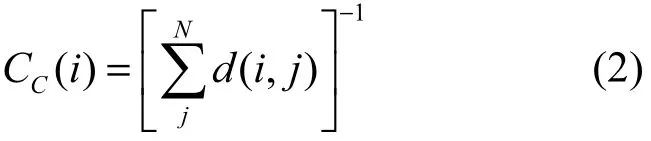
其中，节点i到节点 j的最短路径长度用 (,)d i j表示。

2.3 介数中心性

一个节点的介数中心性衡量了在网络中通过该节点的最短路径的数目，介数中心性分为边介数和点介数[12]。边介数表示网络中所有最短路径中通过该边的最短路径数目占总数的比例。点介数则表示网络中所有最短路径通过该节点的最短路径数目占总数的比例，如式(3)所示。

2.4 K-shell

K-shell[13]分解法是一种粗粒度的网络中节点重要度分析方法，其分解过程如下。从度的角度来看，网络中度为1的节点就是网络中影响力最小的节点（假设网络中不存在度为 0的孤立节点）。把度为 1的节点以及与其相连的边全部去掉，则网络中剩余节点的度相应地发生改变。如果剩余的网络中仍然存在度为1的节点，则重复该操作，直到网络中不存在度为1的节点为止，相当于在网络中一次一次地剥去最外面的壳。称

这些被除去的度为1的节点为1-shell。在网络节点重要性分析过程中，认为在网络中节点对应的K-shell值越大，则节点在网络中的影响力越大。

2.5 特征向量中心性

特征向量中心性也是衡量节点重要程度的一个关键指标。在特征向量中心性的算法中，一个节点的重要程度与其所有邻居节点的重要程度有关。如果一个节点的邻居节点都很重要，则该节点具有很高的重要程度，如式(4)所示。

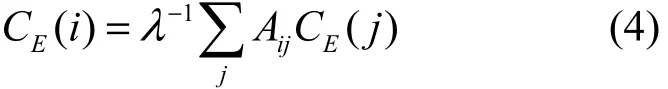
其中，λ为常数，A为网络的邻接矩阵。

2.6 参数比较

上述介绍的5种指标通常均应用于衡量节点在网络中的重要程度。但这几种参数各有长处和不足，简要分析如下。

度中心性的简单性是一个优势，即只需要知道网络中一个节点的局部拓扑结构即可计算其度中心性，但其忽略了节点的全局拓扑的特性，如某个节点虽然与很多节点相连，但它并不处在可以快速获得信息的位置，因此无法成为关键节点。

紧密度中心性定义为从某个节点到其他所有节点的最短路径和的倒数，但紧密度中心性不适用于网络中具有2个不连通组件的情况。假设节点i位于A组件中，节点j位于B组件中，且2个组件不连通，则节点i到节点j的最短路径长度无法计算，因此在计算最短路径和的倒数时会使所有节点的紧密度中心性的值均相同。

介数中心性克服了紧密度中心性的缺点，不仅考虑了全局网络拓扑并且可以应用于具有不连通组件的网络，但介数中心性忽略了不处于任何最短路径上的节点。即介数中心性没有评估在网络中不处于任何最短路径上的节点的中心性。

K-shell分解法是一种粗粒度的方法，在该分解方法中，会存在大量的节点具有相同的 k-shell值，无法进一步区分这些具有相同的k-shell值的节点在网络中的重要程度。

特征向量中心性。若存在2个或多个不同的组件，则邻接矩阵的特征向量只能识别出一个组件，也就意味着特征向量中心性不适用于分析含有多个组件的网络。

综上可知，介数中心性与度中心性以及紧密度中心性相比能够更准确地识别出关键节点，并且适用于更广泛的网络应用场景。K-shell方法需要对网络中的所有节点进行一遍一遍的脱壳处理，过程慢且识别出的节点是粗粒度的，相比介数中心性准确度较低。介数中心性在识别邻接矩阵不对称的网络模型时，较特征向量中心性更具有优势。由于在社交网络中用户之间的关系具有有向性，所以本文基于介数中心性识别舆论领袖节点而实现谣言的抑制。

2.7 基于亲密度算法舆论节点的识别分析

在社交网络中信息传播的过程中，用户节点通常会收到朋友节点的影响。Bakshy[1]以及Onnela[2]通过实验证实了这种说法，并得出信息通过用户节点间的链路进行传播的结论，即熟人传播，因此社交网络展现了“口碑效应”的影响。通过“口碑效应”可以看出，在社交网络中用户之间的关系越亲密，则推荐的消息更容易被接受并加以传播，通过节点间关系的亲密度来实现舆论节点的识别。考虑到社交网络中节点之间信息的传播存在主观因素的影响，所以本文在社交网络中引入了亲密度的概念，并衡量了不相邻节点之间的影响力大小，利用在介数中心性算法的基础上实现舆论领袖节点的识别[14]，并通过对网络中与邻居节点均具有较高的亲密度的节点进行谣言的控制，都会达到较好的效果，本文提出了基于节点亲密度的谣言抑制方法。

节点亲密度的影响因素分析如下。

将社交网络映射为由节点集合V和有向边集合E组成的有向图G=(V,E,W)。将社交网络中的用户集合映射为网络拓扑模型中的节点集合 V；用户之间的关系映射为节点之间的有向链路集合E；W 为链路上的权值，表示每一对用户之间的亲密度量化值。

本文主要从以下3个方面评估节点间的亲密度。1) 交互频率

社交网络中2个节点之间的交互行为是自发的，所以经常会造成2个节点之间存在突发的交互情况。为了防止突发现象的发生，本文取在一段时间内多次交互的时间间隔的平均值作为衡量标准。假设2个节点交互的时间间隔为Δt，一段时间为T，则计算方法如式(5)所示。

其中，n为在时间T内2个节点的交互次数，itΔ表示2个节点第i次和第 1i+次交互的时间间隔。

2) 交互类型

仅通过交互频率来衡量节点的亲密度会出现社交网络中公共账号与用户之间的亲密度异常高的情况。这是因为社交网络中的一些公共账号为了推广自己的产品或广告，会以固定的频率向用户推送消息，导致公共账号与用户之间的交互时间间隔短、交互频率高。在使用交互频率来衡量节点之间的亲密度时忽略了这种情况。为了弥补这个缺点，本文对处于不同好友类型的节点赋予不同的权值。

对使用式(5)计算达到的交互频率赋予权值，如式(6)和式(7)所示。

其中，sw表示2个节点之间的好友类型为陌生人时链路上的权值，fw表示2个节点之间的好友类型为好友时链路上的权值，1η和2η为2个平衡因子，用来协调不同的好友类型的交互频率。

3) 节点间跳数

在以往对社交网络的研究中，没有考虑不相邻节点之间的亲密度，但在社交网络中不相邻的节点之间确实存在亲密度，即“朋友的朋友也是朋友，朋友的敌人就是敌人”。所以不存在直接链路的2个节点不代表没有亲密度。

如图1所示，图中的每个节点表示一个用户，每条链路表示2个节点之间的关系，链路上的权值表示节点之间的亲密度，假设权值越大，则 2个节点之间的亲密度越高，交互越频繁。可以看出，图中节点D和节点E以及节点E和节点B之间的亲密度均较高，且节点D和节点B之间不存在直接链路。若节点D发布一条消息，因为节点D与节点E之间的交互频率较高，所以节点E会很快接收到节点D的消息，并继续传播，则很快节点B就可以通过节点E接收到节点D发送过来的消息。由此可见不相邻的2个节点之间也具有亲密度。

在社交网络中，由于节点之间消息的转发经过每一跳节点的传播时都存在一定的时延。如果在网络中一条路径上节点之间的亲密度均较高，但是跳数较多，则无法直观地判断这条路径传播速度的快慢。因此，需要衡量一条传播路径上每条链路的亲密度大小以及跳数时延带来的影响。如图1所示，从节点A发出一条消息，若该消息传播到节点 B具有 3条路径，分别是 A-＞D-＞E-＞B、A-＞C-＞B和A-＞B。这3条路径的跳数分别为3跳、2跳和1跳。但链路上的亲密度不尽相同，在A-＞D-＞E-＞B这条链路上，每一跳的亲密度均较大，但跳数较多；在A-＞C-＞B和A-＞B这2条路径上，虽然跳数较少，但链路上的亲密度不高，所以无法直观地比较节点A发出的消息从哪条路径能更快地传播到节点B，需要衡量跳数时延和亲密度的大小对传播速度的影响。

图1 节点亲密度以及跳数时延的影响

在信息传播过程中，已有的社交网络中信息扩散程度最大化的研究[15]表明，信息若从节点 i开始传播，则信息在传播了3～4跳之后，则节点i对之后的其他节点几乎没有影响。所以本文也只考虑了某节点与任意距离它间隔3跳之内的节点之间的跳数时延对亲密度的影响。

在社交网络中，消息在节点之间进行传播的过程是相互独立的，即2个节点之间信息的传播速度以及接受程度不受上一跳节点之间传播速度的影响。根据上述分析，得出计算节点间跳数对亲密度的影响公式，如式(8)所示。

其中，γ1和 γ2为2个权值，用来调节交互频率与节点间跳数对亲密度的影响关系，且 γ1, γ2≤ 1；hi,j表示节点i到节点 j之间间隔的跳数，且hi,j≤ 3； wn表示节点i到节点j之间距离节点i的跳数为n的节点 nodei,n与跳数为 n+1的节点nodei,n+1之间链路上的权值，该权值通过式(6)或式(7)计算，如果节点 nodei,n与节点 nodei,n+1之间的关系为陌生人关系，则使用式(6)计算；若为好友关系则使用式(7)进行计算。

在结合了节点之间的交互频率、好友类型和跳数时延3方面综合量化之后，得到最终的节点之间亲密度评估方法。因为在计算网络拓扑中最短路径时，链路上的权值越小表示路径越短，所以将节点间的亲密度量化结果也表示为值越小则亲密度越高。根据介数中心性的大小识别舆论领袖节点，增加了对网络图加边和更新权值的过程，这个过程的时间复杂度是随着节点的增多线性增加的，对每个节点及其邻居节点进行一遍计算。所以整个基于亲密度的舆论领袖节点识别算法的时间复杂度是在 Brande[13]算法的基础上加上更新过程的时间复杂度，为O(nm+n2lbn+ ＜k＞n)。其中，＜k＞为网络平均度的大小。

3 谣言传播模型

由于在社交网络中，每个节点都是一个用户，所以在谣言传播的过程中，每个节点都具备多种不同的状态。在本文的信息扩散模型中，将信息传播过程中的节点分为3种状态：未感染状态、感染状态（infected）和传播状态。

3.1 SIR模型

在经典的SIR传染病模型中，将节点状态分为易感染状态（susceptible）、感染状态和治愈状态（recovered）。社交网络中除传染源之外的节点初始状态均为易感染状态。当处于易感染状态的节点接触到感染节点后以一定的概率变为感染状态。当处于感染状态的节点在接触到易感染状态的节点时，又会以一定的概率将其感染。但当处于感染状态的节点以一定的概率被治愈后，将处于治愈状态，并具有免疫能力，不会再被感染。主要的节点状态转化过程如图2所示。

该传播模型在传染病传播过程中得到广泛应用。适用于当个体感染到病毒后都有成为病原体的机会，并且成为病原体的个体康复后则具有永久免疫能力的情况。

图2 SIR模型中节点状态转化

3.2 SIRS模型

SIRS模型是SIR模型的进一步演化，在SIR模型的基础上增加了从治愈状态到易感染状态的过程。这个过程表示，当个体感染到病原体并被治愈后，并不是处于永久免疫的状态，而是具有一个免疫周期。即处于治愈状态的节点可以以一定的概率丧失自身的免疫能力，恢复到易感染状态。SIRS模型的节点状态转化过程如图3所示。

图3 SIRS模型中节点状态转化

3.3 SEIR模型

SEIR模型在 SIR模型中添加了潜伏状态（exposed）。当处于易感染状态的节点与处于感染状态的节点接触后，并不是以一定的概率转变为感染节点，而是先以一定的概率转变为潜伏状态。处于潜伏状态的节点仍然是一个健康的个体，不具备传染其他节点的能力。然后处于潜伏状态的节点会以一定的概率转变为感染状态。与 SIR模型相同，SEIR模型中处于治愈状态的节点也具有了永久免疫的能力。这种模型更适用于描述具有典型潜伏期的传染现象，如狂犬病，感染后并不是马上发病，而是潜伏一段时间后以一定的概率发病。所以在社交网络中这种模型并不是十分实用，因为在社交网络中用户对接收到的信息具有即时反馈特性。即时反馈特性指当用户收到消息后会马上做出反馈，无论是选择转发还是评论，都会在接收到信息后做出该行为。

SEIR模型的节点状态转化过程如图4所示。

图4 SEIR模型中节点状态转化

3.4 传染病模型改进

通过向社交网络中的舆论领袖节点注入真相从而控制社交网络中谣言的传播。因此在这一部分将社交网络中节点传播的状态进一步细化，其中包含了当节点接收到真相后的各种状态。

1) 易感染状态。处于易感染状态的节点既没有接收过谣言的信息也没有接收过真相的信息。处于该状态的节点很容易以一定的概率被谣言或真相感染。假设节点i处于易感染状态，

当其接收到关于谣言的信息，则以概率λ选择相信谣言，变为感染状态。若节点i接收到的是关于真相的信息，则以概率β选择相信真相，变为免疫节点。

2) 感染状态。处于感染状态的节点具有传染性。该状态的节点具有将谣言传播给其他节点的能力。但当处于感染状态的节点接收到真相相关的信息后则以概率α选择相信真相，变为治愈状态。

3) 治愈状态。处于治愈状态的节点不再相信谣言，并以一定的概率传播真相。由于在社交网络中，每一个节点都是现实生活中的一个个体，具有记忆机制，所以处于治愈状态的节点同样也属于免疫状态。

4) 免疫状态（defended）。当处于易感染状态的节点接收到真相后选择了相信真相，则会进入免疫状态。处于该状态的节点通常具有较强的自我判断能力。

通过上述对抑制谣言过程中节点状态的分类，总结社交网络中节点状态变化过程，如图 5所示。上述过程在SIR模型的基础上增加了免疫状态，更形象地描述了社交网络中的节点直接相信真相的过程。

图5 抑制谣言过程中节点状态转化

处于免疫状态和传播状态的节点都具有2种状态：活跃状态（active）和不活跃状态（inactive）。处于活跃状态的节点具有感染其他节点的能力，继续将谣言或真相传播给其他节点。而处于不活跃状态的节点则不具备传播信息的能力，处于感染状态的不活跃节点继续保持自身原有状态直到接触到免疫节点后以一定的概率转变为治愈状态，处于免疫状态的不活跃节点则始终保持自身原有状态不变。

假设节点i在 t时刻处于易受感染状态或感染状态，则节点i在下一时刻接收到其邻居节点传播的真相的概率如式(9)所示。

其中， nei( i)表示节点i的邻居节点集合， wi,j表示节点i和节点j之间的亲密度， Xj(t)表示节点j在t时刻所处的状态，Pj( Xj(t) =refended. a ctive)表示节点j在 t时刻处于免疫状态下的活跃状态的概率。只要节点i在t+1时刻接受了任何一个其处于免疫状态的邻居节点传播的真相，则节点 i将会变为免疫状态。

由此可知，在网络中的任意一个节点接受真相的平均时间如式(10)所示。

假设节点i在t时刻处于易受感染状态，而在t+1时刻仍然处于易受感染状态的概率如式(11)所示。

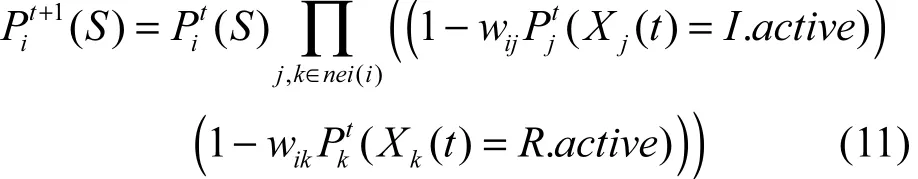
其中， ()t iP S表示节点i在t时刻处于易受感染状态的概率，节点j表示节点i的邻居节点中在t时刻处于感染状态并活跃的节点，节点k表示节点i的论据节点中在t时刻处于免疫状态并活跃的节点。若节点在t+1时刻仍然处于易受感染状态，则说明其邻居节点对其任何消息的传播均没有被接受。

同理，可以推导出节点在任意时刻处于某种状态的概率。节点i在t+1时刻处于感染状态的概率以及处于免疫状态的概率分别如式(12)和式(13)所示。

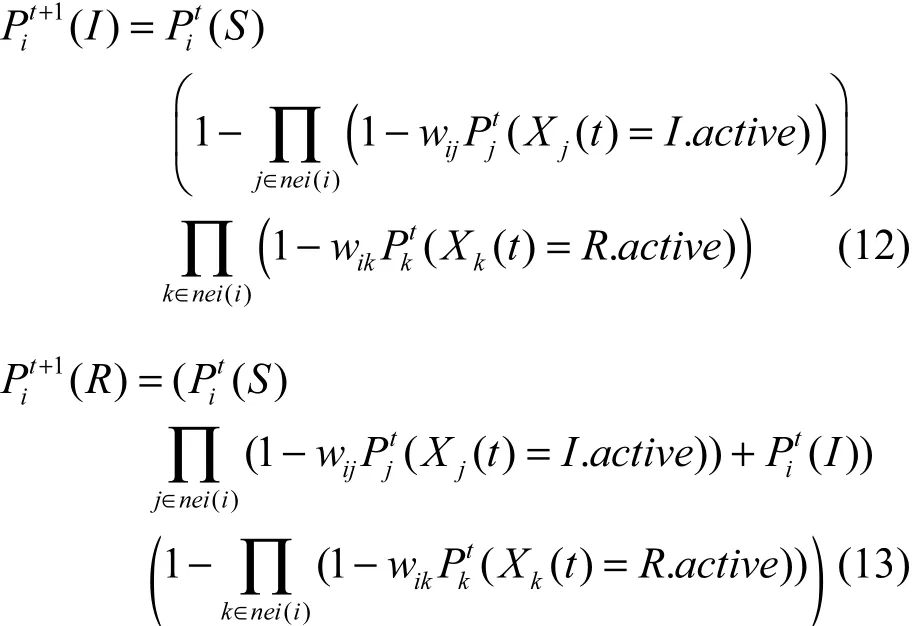
通过上述分析可以看出，社交网络中处于免疫状态的节点与其邻居节点之间的亲密度越大，则处于免疫状态的节点传播的真相信息更容易被其邻居节点接受，从而使真相能够在整个网络中迅速传播，进而达到快速控制谣言的目的。

4 仿真实验

对于谣言控制，若通过网络中的关键节点实现谣言的阻塞，但是谣言的传播迅速，往往当人们了解到谣言信息时，谣言传播已达到一定的范围。为挽救谣言散播的局面，此时就需要补救措施进行补救，通过舆论领袖节点向整个网络中注入与谣言相对的真实信息，当真实信息与谣言先后达到某个节点时，该节点对于信息的真实度会重新判断，同时，当散播真实信息的节点亲密度较高时，会降低谣言的可信度。整个网络中不再存在接收谣言信息的节点，但是这种状态基本不能实现[9]，因此为实现谣言的控制，应在最短的时间内，将信任谣言信息的节点控制在一定的范围内。

4.1 信息最大化扩散效果比较

为验证基于节点间亲密度对于谣言控制的有效性，分别使用随机选取、度中心性选取、介数中心性选取和基于亲密度选取，在1 000个节点和2 000个节点的网络模型中识别出10个舆论领袖节点作为信息源，比较最终被信息感染节点的数目。具有1 000个节点的网络中选取10个节点作为信息源，得到最终感染节点数目，即最大化扩散效果对比方法，实验结果如图6所示，根据亲密度方法选择的舆论领袖节点最大化扩散过程仍然是一个慢起步的过程，但最终的最大化扩散规模较其他2种方法大。

其中，closeness表示通过基于亲密度识别舆论领袖节点的方法；random表示随机选取方法；degree表示通过度中心性选取舆论领袖节点的方法；betweenness表示使用介数中心性识别方法识别的舆论领袖节点扩散过程。

在2 000个节点的网络中选取10个节点作为信息源，得到最终感染节点数目，即最大化扩散效果对比方法，实验结果如图7所示。

由于随机选取的节点具有随机性，所以在本次对比实验中，随机选取的舆论领袖节点没有办法扩散信息。度中心性和亲密度选取的舆论领袖节点在影响力最大化扩散效果中，可以与有1 000个节点以及2 000个节点的网络得到相同的结论。

4.2 谣言抑制效果对比

将改进的谣言传播模型引入到独立级联模型中，增加独立级联模型中节点的状态，并分别从以下几方面进行谣言抑制扩散效果对比。

1) 真相注入时间不同

本节分别对比不同的真相注入时间t对谣言抑制效果的影响，结果如图8所示。分别对比了真相在不同时刻t=2、t=3和t=4注入到网络中的情况，其中，时间t表示在真相的注入时刻，t=2为较早时刻，t=3为中间时刻，t=4表示较晚时刻。从图8中可以看出，真相注入的时间越早，则可以越好地抑制谣言的传播范围。

图6 1 000个节点的网络中，最大化扩散效果

图7 2 000个节点的网络中，最大化扩散效果

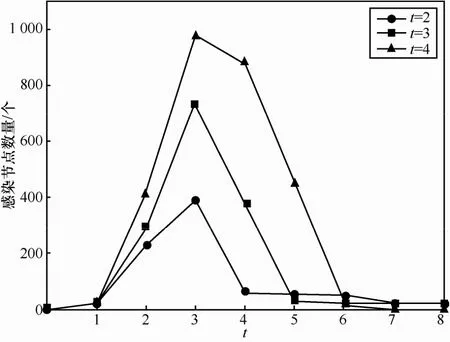
图8 不同时间注入真相的谣言抑制效果对比

2) 舆论领袖节点不同

本节分别对使用不同的舆论领袖节点识别方法识别出的节点在相同的时间注入真相，并对比其谣言抑制效果。

图9表示在相同的时间分别向多种方法识别出的舆论领袖节点注入真相（在较晚时刻）抑制谣言的效果对比情况。从图9可以看出，向使用度中心性识别出的舆论领袖节点注入真相后，被谣言感染的节点数量依然有一个上升的趋势，然后才开始逐渐被抑制。

从图9(b)可以看出，介数中心性识别方法与基于亲密度识别舆论领袖节点的方法在抑制谣言的过程中，初始阶段相差不大，均在注入真相后就会对谣言有显著的抑制作用，但之后亲密度方法抑制谣言的速度较介数中心性方法更快，所以，亲密度方法对谣言抑制速度较快，能较早达到稳定状态，控制效果较好。

5 结束语

本文首先分析了谣言传播模型，以及谣言在社交网络中传播时节点的状态转化过程。其次通

过数值分析的方法提出了一种基于亲密度的谣言抑制方案，并通过理论分析和仿真对比验证了该方案的有效性。本文从社交网络节点间亲密的角度识别了社交网络中的舆论领袖节点，并取得了一定的研究成果[14]，但识别舆论领袖节点最终的目的是为了更好地控制社交网络。本文虽然给出了基于舆论领袖节点的谣言控制方法，但只是从数值分析和理论分析的角度进行了阐述，仍需要深入探索。

[1] BAKSHY E, KARRER B, ADAMIC L A. Social influence and the diffusion of user-created content[C]//The 10th ACM Conference on Electronic Commerce. 2009: 325-334.

[2] ONNELA J P, SARAMÄKI J, HYVÖNEN J, et al. Structure and tie strengths in mobile communication networks[J]. The National Academy of Sciences, 2007, 104(18): 7332-7336.

[3] SOH D W, QUEK T Q S, TAY W P. Randomized rumor spreading in non-static networks[C]// IEEE International Conference on ICT Convergence. 2011:156 - 160.

[4] PANAGIOTOU K, PÉREZGIMÉNEZ X, SUN T S H. Randomized rumour spreading: the effect of the network topology[J]. Combinatorics Probability & Computing, 2014, 24(2):1-23.

[5] ACAN H, COLLEVECCHIO A, MEHRABIAN A, et al. On the push&pull protocol for rumour spreading[J]. Klinische Padiatrie, 2014, 226(3):161-168.

[6] FOUNTOULAKIS N, HUBER A, PANAGIOTOU K. Reliable broadcasting in random networks and the effect of density[C]// Infocom. 2010:1-9.

[7] GIAKKOUPIS G. Tight bounds for rumor spreading in graphs of a given conductance[C]//The 28th International Symposium on Theoretical Aspects of Computer Science (STACS 2011). 2011: 57-68.

[8] CHIERICHETTI F, LATTANZI S, PANCONESI A. Almost tight bounds for rumour spreading with conductance.[J]. The ACM International Symposium on Theory of Computing, 2010:399-408.

[9] WEN S, JIANG J, XIANG Y, et al. To shut them up or to clarify: restraining the spread of rumors in online social networks[J]. Parallel and Distributed Systems, 2014, 25(12): 3306-3316.

[10] AI J, ZHAO H, CARLEY K M, et al. Neighbor vector centrality of complex networks based on neighbors degree distribution[J]. Physics of Condensed Matter, 2013, 86(4):1-7.

[11] WEHMUTH K, ZIVIANI A. Distributed assessment of the closeness centrality ranking in complex networks[C]// The Workshop on Simplifying Complex Networks for Practitioners. 2012:43-48.

[12] BRANDESU. A faster algorithm for betweenness centrality[J]. Journal of Mathematical Sociology, 2010, 25(2):163-177.

[13] KITSAK M, GALLOS L K, HAVLIN S, et al. Identification of influential spreaders in complex networks[J]. Nature Physics, 2010, 6(11): 888-893.

[14] YANG L, QIAO Y, LIU Z, et al. Identifying opinion leader nodes in online social networks with a new closeness evaluation algorithm[J]. Soft Computing, 2016:1-12.

[15] LU Z, FAN L, WU W, et al. Efficient influence spread estimation for influence maximization under the linear threshold model[J]. Computational Social Networks, 2014, 1(1): 1-19.

田亚平（1991-），女，河北保定人，西安电子科技大学硕士生，主要研究方向为复杂网络、移动和无线网络安全。

杨力（1977-），男，陕西西安人，博士，西安电子科技大学副教授、硕士生导师，主要研究方向为移动互联网安全——认证方法与技术、云计算安全、数据安全存储与删除、移动终端安全、运行环境安全验证、可信计算、远程证明技术。

王小琴（1990-），女，山西长治人，西安电子科技大学硕士生，主要研究方向为复杂网络、移动和无线网络安全。

乔雅峰（1993-），女，内蒙古呼伦贝尔人，西安电子科技大学硕士生，主要研究方向为复杂网络、移动和无线网络安全。

Suppress the diffusion of rumors with nodes closeness mining

TIAN Ya-ping, YANG Li, WANG Xiao-qin, QIAO Ya-feng
(School of Cyber Engineering, Xidian University, Xi’an 710071, China)

Through making the analysis of information spread in social networks, the supression of rumors, error information and other negative information was realized. Firstly, by analyzing the structure of social networks and the characteristics of node behavior, a method for the identification of opinion leader nodes was proposed based on the degree of intimacy between nodes in social networks. Then, the rumor propagation model and the analysis of nodes’ state transformation process were made when the rumor spread in social networks. At last, the control method was proposed to suppress the diffusion of rumors with the nodes’ closeness.

rumor propagation model, closeness, social networks, supression of rumors

TP393

A

10.11959/j.issn.2096-109x.2016.00114

2016-09-20；

2016-10-23。通信作者：田亚平，typ19920110@sina.com

国家自然科学基金资助项目（No.61671360）；信息保障重点实验室基金资助项目（No.KJ-14-109）；中央高校基本科研业务费基金资助项目（No.JB161505）

Foundation Items: The National Natural Science Foundation of China (No.61671360), The Foundation of Science and Technology on Information Assurance Laboratory (No.KJ-14-109), The Fundamental Research Funds for the Central Universities (No.JB161505)