大跨度悬索桥正交异性板钢箱梁施工中横向应力分布规律研究

2016-12-12危媛丞李周郑荧光褚东升闵世超

公路与汽运 2016年6期

危媛丞，李周，郑荧光，褚东升，闵世超

（1.深圳市龙华新区大浪办事处建设工程事务中心，广东深圳 518109；2.中建钢构有限公司，广东深圳 518048；3.湖南大学，湖南长沙 410082；4.中交第四航务工程勘察设计院有限公司，广东广州 510230；5.华东交通大学，江西南昌 330013）

危媛丞1，李周2，3，郑荧光2，褚东升4，闵世超5

以郑州潮河大桥为工程依托，对正交异性板钢箱梁施工过程中的空间应力状况进行现场实测和有限元模拟，对比分析其横向应力分布特点。结果表明，现场实测与有限元计算所得分布规律基本吻合，施工过程中钢箱梁横向应力具有较大的安全储备；沿桥跨方向，主塔截面位置顶、底板横向应力值较大；沿横截面方向，横截面中心位置横向应力较大；钢箱梁横向处于下挠状态；完成桥面铺装时钢箱梁顶、底板横向应力沿桥跨方向分布更均匀。

桥梁；大跨度悬索桥；正交异性板钢箱梁；横向应力

在各种桥梁结构体系中，悬索桥是跨越能力最强的桥型，也是景观效果较好的桥型之一。无论是大跨度公路桥，还是景观要求较高的城市道路桥梁，悬索桥都得到了广泛运用，而这些桥梁大多采用正交异性桥面板钢箱梁结构形式。

正交异性板钢箱梁具有高度低、自重轻、极限承载力大、易于加工制造等优点，但其制造要求较高、结构受力复杂。国内已开展很多相关研究，如程建华、邢中凯分析了钢箱梁正交异性桥面板的受力特性和计算方法，郁春松、张陕锋研究了正交异性板钢箱梁的计算与结构优化问题，杨灿、段政、孔祥福研究了正交异性板钢箱梁的空间应力、局部应力分布规律和受力性能；刘信斌、衣龙泉分析了钢箱梁剪力滞系数的横向变化规律。但对正交异性板钢箱梁施工过程中横向应力的研究较少。该文以郑州潮河大桥为工程依托，对正交异性板钢箱梁的空间应力状况进行现场实测和有限元模拟，研究大跨度悬索桥正交异性板钢箱梁施工中的应力特点。

1 工程概况

郑州潮河大桥为郑州经济开发区滨河国际新城经南八路跨越潮河的一个节点工程，为三塔四跨地锚式悬索桥，跨径布置为（64+136+136+64）m= 400 m。悬索桥加劲梁采用全焊钢箱梁结构，顶宽45 m，中线处梁高2 m，悬臂板长5.808 m。全桥钢箱梁分为四类（见图1）：Z1为标准段，长6 m；Z2为

合龙段，长3.7 m；Z3为中塔、边塔段，长12.3 m；Z4为端横梁位置，长3.69 m。钢箱梁节段之间采用焊接连接。钢箱梁钢材采用Q345qD，桥面板采用正交异性板构造，纵向加劲肋为U形肋，顶板U形肋间距600 mm；底板机动车道范围加劲肋采用U形肋，间距800mm，其余部分采用板肋，间距420 mm。钢箱梁每隔3 m设一道标准横隔板。钢箱梁截面构造见图2。

图1 半桥钢箱梁节段划分示意图（单位：mm）

图2 钢箱梁截面构造示意图（单位：mm）

2 现场测试方案

2.1 测点布置

选取边跨跨中、边主塔、中跨1／4跨、中跨1／2跨、中跨3／4跨和中主塔（分别为S1～S6）作为应变测点布置控制断面（见图3），其中：S1截面距边跨梁端32 m；S2截面距边跨梁端64 m；S3截面距边跨梁端98 m；S4截面距边跨梁端132 m；S5截面距边跨梁端166 m；S6截面距边跨梁端200 m。

图3 钢箱梁应变测点布置断面（单位：cm）

每个控制断面顶、底板各布置3个横向应变计、6个测点，全桥共36个测点，横向具体位置为两吊索及梁截面中心处，采用XHX-21x型振弦式表面应变计（见图4）。

图4 钢箱梁横向应变计布置（单位：mm）

2.2 测试工况

该桥吊索共进行三轮张拉，前两轮张拉过程中胎架未拆除，钢箱梁应力较小，可不予考虑。第三轮张拉开始后，尤其是在胎架拆除后，钢箱梁各测点应力较大，应力测试主要针对这一情况。设置两种测试工况：工况1为拆除胎架；工况2为施工第二层沥青砼铺装，成桥。吊索编号见图5，测试工况下钢箱梁吊索张拉力见表1。

图5 吊索布置及编号

表1 各测试工况下吊索张拉力

3 测试结果分析

3.1 有限元计算模型

为分析现场实测结果的合理性，采用ANSYS软件建立钢箱梁三维有限元模型进行比较分析。

考虑到桥塔高度较小而刚度较大，不建立桥塔模型而仅在塔梁相交处施加对应支座约束；因分析对象是钢箱梁，不建立缆索系统而在相应节点处施加竖向拉力来模拟吊索张拉力；考虑到结构和荷载的对称性，仅建立全桥钢箱梁的1／4模型（见图6）。

模型共划分为149 349个单元，钢箱梁结构均采用三维四节点单元Shell181模拟。计算工况与测试工况一致，工况1时在钢箱梁吊点处施加竖向力来模拟吊索张拉力，工况2时机动车道二期恒载取4.13 k N／m2，索区、人行道、非机动车道二期恒载取3.00 k N／m2。

图6 钢箱梁1／4有限元模型

3.2 横向应力沿桥跨方向的分布规律

横向应力沿桥跨方向的分布见图7、图8。

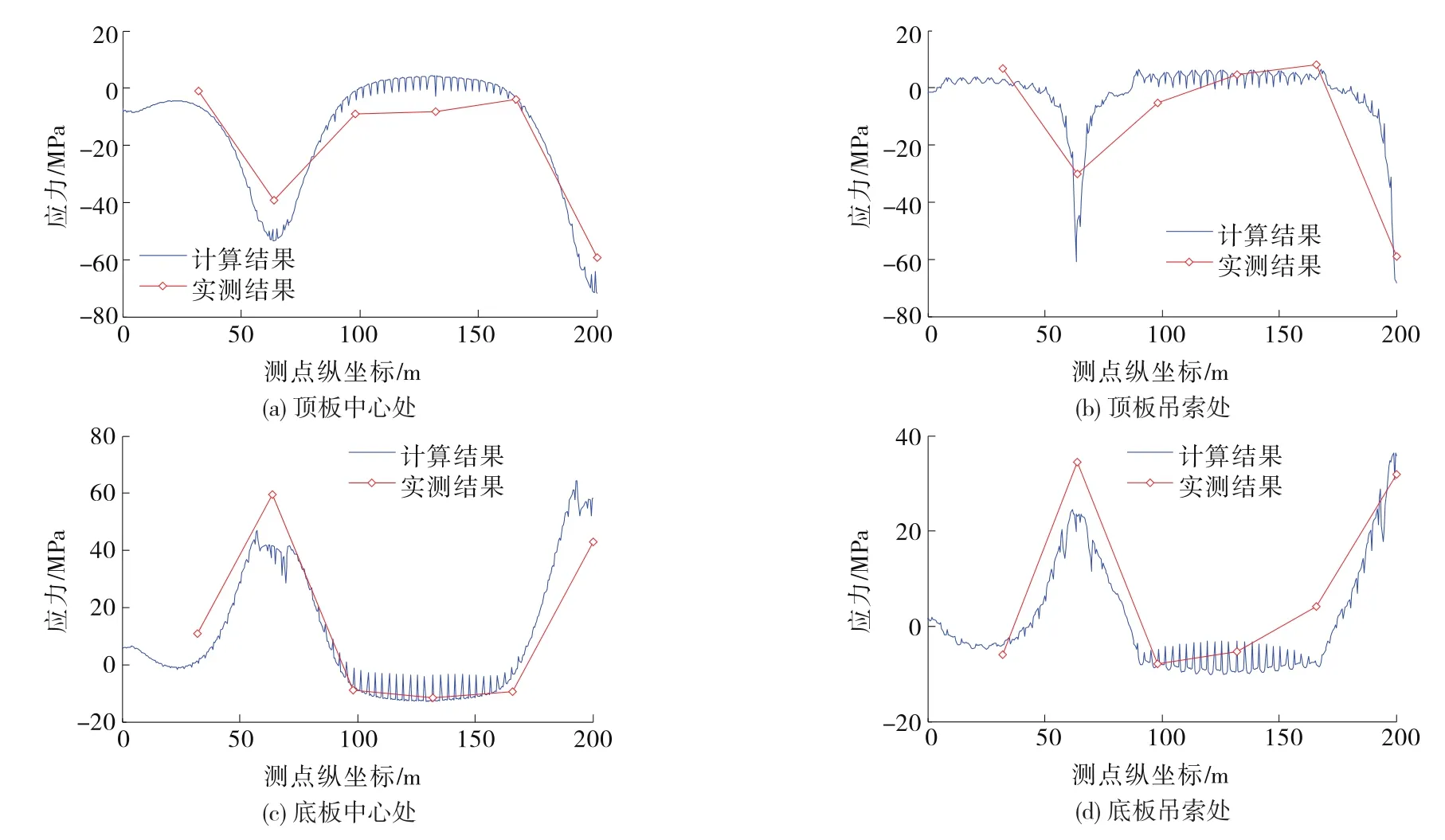
图7 工况1钢箱梁横向应力沿桥跨的分布

由图7、图8可知：工况1时S2、S6截面位置钢箱梁顶、底板横向应力较大，最大值约70 MPa，其余截面位置横向应力相对较小。S2、S6截面位置钢箱梁顶板受横向压应力、底板受横向拉应力，说明钢箱梁横向处于下挠状态。与工况1相比，工况2时钢箱梁顶、底板横向应力沿桥跨方向的分布更均匀，沿桥跨方向顶板横向应力基本为负值（即顶板横向受压），底板横向应力基本为正值（即底板横向受拉），钢箱梁横向处于下挠状态，但横向应力都很小，最大值不超过40 MPa，比工况1时的横向应力峰值大幅减小。

各测点横向应力实测结果与计算结果对比见表2。从表2可看出：1）各测点实测横向应力沿桥跨的分布与计算结果基本吻合，但存在一定误差，部分测点相对误差超过100%，甚至达到数倍。考虑到天气条件、安装和测试人员的操作规范与否、施工人员及施工机具的直接或间接作用、吊索张拉力是否精确等大量随机因素的影响，部分测点出现较大误差是正常的。相对误差较大的测点一般横向应力较小，而横向应力较大的测点其实测值与计算值较接近，实测结果与计算结果所得出的分布规律基本吻合，都基本可以反映钢箱梁顶、底板横向应力特征，说明实测方法及结果可靠，有限元计算模型合理。

2）S2、S6截面处钢箱梁顶、底板的横向应力相对较大，实测和计算横向应力最大值分别为59.34、71.93 MPa，均发生在工况1中跨主塔截面的顶板中心处，具有较大的安全储备。而非主塔位置的S1、S3、S4、S5截面处钢箱梁顶、底板的横向应力均较小，两种工况下实测和计算横向应力最大值均不超过40 MPa，大部分测点横向应力在20MPa以内，具有很大的安全储备。

图8 工况2钢箱梁横向应力沿桥跨的分布

表2 各测点横向应力实测结果与计算结果对比

3.3 横向应力沿横截面方向的分布规律

受测点数量的限制，不能同时沿桥纵向和横向布置较多的横向应变计。在钢箱梁顶、底板横向应变计布置过程中侧重考虑钢箱梁顶、底板横向应力沿桥跨方向的分布，在测点布置上沿桥跨选择较多的测试截面（S1～S6）。在每个横截面上仅在预设的关键位置（梁截面中心及两侧吊索位置附近）布置测点，对于1／4模型的钢箱梁顶、底板横向应力来说，S1～S6每个断面都分别仅有2个测点，仅根据实测数据并不能得出钢箱梁顶、底板横向应力沿横截面方向的分布规律，无法确定在横截面的哪个位置横向应力最不利。

在实测与计算所得出的横向应力沿桥跨分布规律基本吻合、有限元计算结果合理性得到实测结果验证的前提下，可仅通过有限元计算结果来分析钢箱梁顶、底板横向应力沿横截面方向的分布规律（见图9、图10）。

从图9、图10可以看出：钢箱梁顶、底板横向应力在横坐标为零处达到最大，即横截面中心处钢箱梁横向应力值最大，但最大值不超过80 MPa，相对于Q345qD的容许弯曲应力210 MPa而言，具有很大的安全储备。