课堂实录：一个疑问引发的风波

杨平

（广东省肇庆市端州区肇庆中学高中部）

课堂实录：一个疑问引发的风波

杨平

（广东省肇庆市端州区肇庆中学高中部）

在教学直线与双曲线的位置关系时，为了让学生更直观地了解直线与双曲线的交点情况，借用GeoGebra软件进行演示。在演示中通过一个学生的疑问引导学生通过观察、大胆质疑、自主探究、实践求证，让学生在数形结合的基础上深入探讨了直线与双曲线的相关知识。

直线；双曲线；数形结合；GeoGebra

GeoGebra是一个结合几何、代数与微积分的动态数学软件，它是由美国佛罗里达州亚特兰大学的数学教授Markus Hohenwarter设计的，GeoGebra融合了代数与几何两大学科，做到了图形与代数方程的同步变化，实现了真正的动态演示。可以通过在下方的命令输入框输入圆锥曲线方程的方式（如输入“x^2+ y^2=1”）直接画出图形，甚至可以用向量运算的方式输入（A+B+ C）/3来直接显示△ABC的重心点。

一、波澜不惊：常规教学在信息展示中传授知识

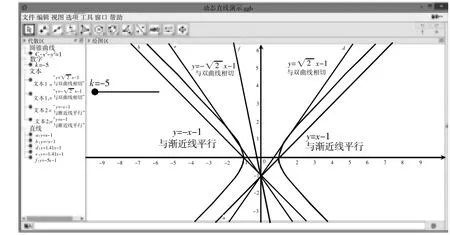
在介绍直线与双曲线的位置关系时，教师可以通过一个思考题来探究：讨论直线y=kx-1与双曲线x2-y2=1的交点个数，并求此时k的取值范围。

代数解析不再赘述。为了让学生更形象地理解直线与双曲线的位置关系，利用GeoGebra软件进行了下面设计：

①先在“输入框”中分别输入并回车：x^2-y^2=1，y=x，y=-x，得到双曲线及其渐近线的图象，可以很清晰地让学生理解相切与只有一个交点的区别与联系；

②在输入框中输入：y=kx-1，并回车，此时会弹出“创建滑动条”的对话框，根据需要产生一个关于变量k的滑动条（如下图所示）。拉动滑动条，可让学生与上面的代数式进行验证。

二、风波乍起：点滴疑问在拓展思维中放飞思想

1.一个学生的积极归纳：

2.一个学生的无意提问：是否所有直线与双曲线的位置关系都可以利用上面的数轴来实现呢？

3.要回答学生提出的问题，结合学生的尝试和探讨，教师可利用GeoGebra进行如下设计：

（1）先实现双曲线x2-y2=1及其渐近线的图象；

（2）在输入框中输入：y=tan（a）*（x-p）+q，其中a∈［0，3.14］，p∈［-5，5］，q∈［-5，5］，从而形成过点M（p，q）的动直线d；

（3）在输入框中分别输入：y=（x-p）+q与y=-（x-p）+q，回车后形成过点M（p，q）的两条与双曲线渐近线平行的伴随动直线；

（4）可以拖动点M，让它位于不同的位置，再拖动参数a，观察动直线d与双曲线的交点情况。如下图1所示：

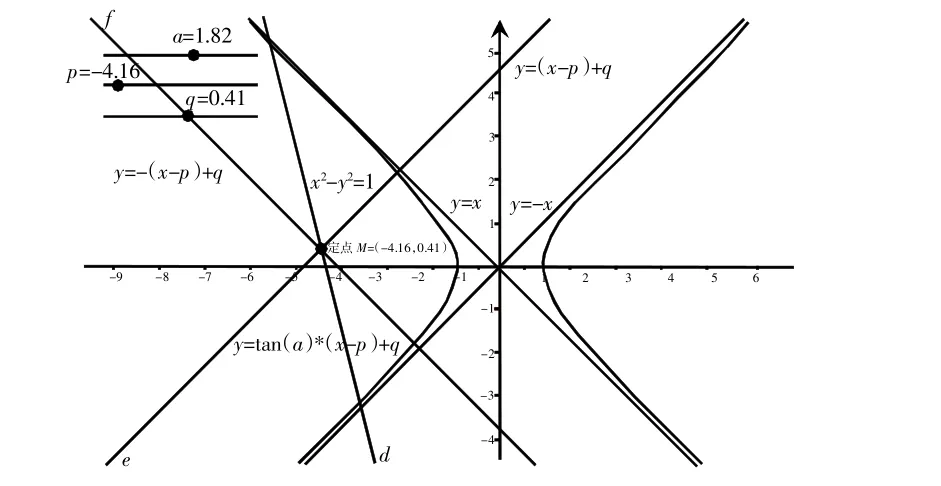
图1

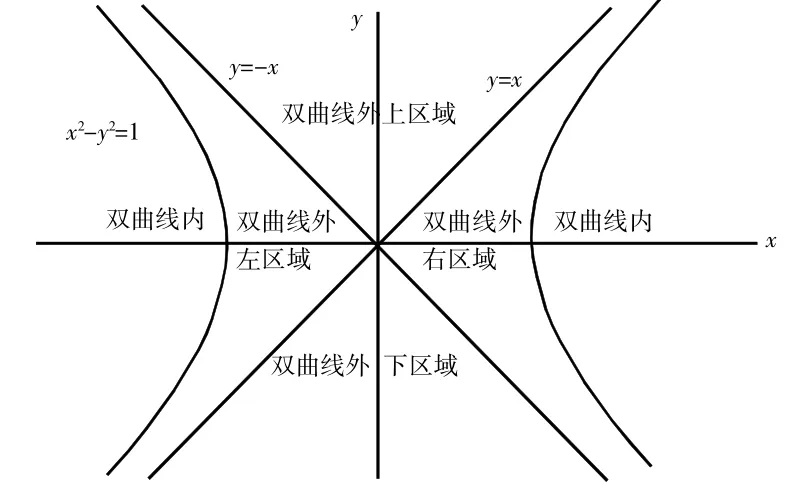
图2

（I）先研究直线与双曲线只有一个交点的情形：将双曲线包含两个焦点的区域简称为双曲线内，含有原点的区域简称为双曲线外，如上图2所示。通过定位点M（p，q）在图2中的不同区域，可以观察到下列情形：

①当点M在双曲线内时，有两条与双曲线渐近线平行的直线与双曲线只有一个交点；

②当点M在双曲线上或点M在双曲线的渐近线上（除原点）时，有三条直线与双曲线只有一个交点：两条与双曲线渐近线平行的直线和一条与双曲线相切的直线；

③当点M在双曲线外左（右、上、下）区域时，有四条直线与双曲线只有一个交点：两条与双曲线渐近线平行的直线和两条与双曲线相切的直线；

④当点M在原点处时，有两条与双曲线渐近线重合的直线与双曲线只有一个交点。

（II）利用检验直线快速判断直线与双曲线的交点个数及此时所对应的直线斜率的变化范围。下面是点M在双曲线外左区域的检验图形及结论。

这样，我们就可以很快得到上面右方的结论，这也形成了解决直线与双曲线交点问题的几何法。

三、余波阵阵：大胆猜想在细致观察中迸发灵感

1.通过观察图形的变化，学生大胆猜测：切线的斜率应该大于或小于。

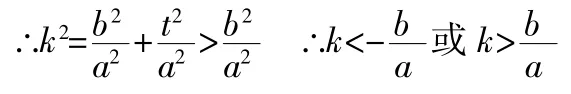
2.从图象上思考：当点M位于渐近线上时，直线与双曲线只有一条切线；当点M在双曲线上时，直线与双曲线只有一条切线，这两种情形是否都意味着Δ=0时斜率k有两个相等的实数根？

∴（p2-a2）x2-2pqk+q2+b2=0（※）

（1）当点M在x=±a上时，此时一条切线是x=±a，另一条切线的斜率为

（3）当点M位于双曲线上时，则有b2p2-a2q2=a2b2，而（※）的Δ=（-2pq）2-4（p2-a2）（q2+b2）=0，有两个相等的实数根。

四、波光粼粼：兴趣探究在自我实践中彰显智慧

1.学生很好奇地利用GeoGebra软件进行抛物线的自主学习。

2.学生很成功地利用GeoGebra软件进行了双曲线与椭圆等轨迹方程的再探究。

郭沫若老先生说过：“教育的目的是养成自己学习、自由研究、用自己的头脑来想、用自己的手来做的这种精神。”课堂是老师的生命力所在地，是学生智慧的发源地。为了让学生动起来，让课堂活起来，让爱充满整个课堂，让学生在朴素的课堂生活中去品味自然科学，我们要用师生之间的爱唤起学生的求知欲，用技巧引导学生全面和谐的发展，给学生创造一个民主和谐的发展空间。“数形结合拓思维，代数解析定经纬”，这堂课借用学生的疑问，引导学生自主观察、大胆猜想、实践求证、合作交流，让学生真正成为课堂的主人。最有意义的是学生学会了使用数学工具软件，并使之成为数学学习的重要助力。

詹文艺.过定点的直线与双曲线的公共点问题浅析［J］.学法指导，2013（41）：95-96.

·编辑杨国蓉

杨平，男（1979—），硕士研究生，广东省肇庆市端州区肇庆中学高中部数学教师。